- Erratum
- Open access
- Published:
Erratum to "Iterative Methods for Variational Inequalities over the Intersection of the Fixed Points Set of a Nonexpansive Semigroup in Banach Spaces"
Fixed Point Theory and Applications volume 2011, Article number: 187439 (2011)
In my recent published paper [1] to prove Lemmas 3.1 and 5.1, an inequality involving the single-valued normalized duality mapping  from
from  into
into  has been used that generally turns out there is no certainty about its accuracy. In this erratum we fix this problem by imposing additional assumptions in a way that the proofs of the main theorems do not change.
has been used that generally turns out there is no certainty about its accuracy. In this erratum we fix this problem by imposing additional assumptions in a way that the proofs of the main theorems do not change.
We recall that a uniformly smooth Banach space  is
is  -uniformly smooth for
-uniformly smooth for  if and only if there exists a constant
if and only if there exists a constant  such that, for all
such that, for all  ,
,

for more details see [2]. Therefore, if  , then there exists a constant
, then there exists a constant  such that
such that

It is well known that Hilbert spaces,  and
and  for
for  , are 2-uniformly smooth.
, are 2-uniformly smooth.
Throughout the paper we suggest to impose one of the following conditions:
(a) the Banach space  is 2-uniformly smooth;
is 2-uniformly smooth;
(b) there exists a constant  for which
for which  satisfies the following inequality:
satisfies the following inequality:

for all  .
.
Remark 1.1.
If  is
is  -Lipschitzian, then
-Lipschitzian, then  satisfies (3) and is norm-to-norm uniformly continues that suffices to guarantee that
satisfies (3) and is norm-to-norm uniformly continues that suffices to guarantee that  is 2-uniformly smooth. For more results concerning
is 2-uniformly smooth. For more results concerning  -Lipschitzian normalized duality mapping see [3].
-Lipschitzian normalized duality mapping see [3].
Note that since every uniformly smooth Banach space  has a Gateaux differentiable norm and each nonempty, bounded, closed, and convex subset of
has a Gateaux differentiable norm and each nonempty, bounded, closed, and convex subset of  has common fixed point property for nonexpansive mappings, we have
has common fixed point property for nonexpansive mappings, we have  in [1]. So, when
in [1]. So, when  is 2-uniformly smooth, we can remove these two conditions from Theorems 3.2, 4.2, and 5.2 in [1].
is 2-uniformly smooth, we can remove these two conditions from Theorems 3.2, 4.2, and 5.2 in [1].
Considering the above discussion to complete our paper, we reprove Lemmas 3.1 and 5.1 of [1] here with some little changes.
Lemma 3.1 (see [1]).
Either let  be a real Banach space, and let
be a real Banach space, and let  be the single-valued normalized duality mapping from
be the single-valued normalized duality mapping from  into
into  satisfing (3) or let
satisfing (3) or let  be a 2-uniformly smooth real Banach space. Assume that
be a 2-uniformly smooth real Banach space. Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian on
-Lipschitzian on  . Then
. Then

is a contraction on  for every
for every  .
.
Proof.
If  satisfies (3), considering the inequality
satisfies (3), considering the inequality

for all  , we have
, we have

Clearly, the same inequality holds if  is a 2-uniformly smooth real Banach space. Thus, we obtain
is a 2-uniformly smooth real Banach space. Thus, we obtain

With no loss of generality we can take  ; therefore, if
; therefore, if  , then we have
, then we have  ; that is,
; that is,  is a contraction, and the proof is complete.
is a contraction, and the proof is complete.
Also Lemma 5.1, which is easily proved in the same way as Lemma 3.1, will be as follows.
Lemma 5.1 (see [1]).
Either let  be a real Banach space, and let
be a real Banach space, and let  be the single-valued normalized duality mapping from
be the single-valued normalized duality mapping from  into
into  satisfing (3), or let
satisfing (3), or let  be a 2-uniformly smooth real Banach space. Assume that
be a 2-uniformly smooth real Banach space. Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian on
-Lipschitzian on  . If
. If  , where
, where  , then
, then

is a contraction on  .
.
With the new imposed conditions and considering the above lemmas, the following corrections should be done in [1]:
(1)in Theorem 3.2 and Theorem 4.2,  ;
;
(2)in Theorem 5.2,  , where
, where  ;
;
(3)in Remark 5.3,  , where
, where  .
.
Also in [1, Corollary 4.3] the real Banach space  does not necessarily need to have a uniformly Gateaux differentiable norm.
does not necessarily need to have a uniformly Gateaux differentiable norm.
To avoid any ambiguity in terminology note also that  -strongly monotone mappings in Banach spaces are usually called
-strongly monotone mappings in Banach spaces are usually called  -strongly accretive.
-strongly accretive.
References
Mohamadi I: Iterative methods for variational inequalities over the intersection of the fixed points set of a nonexpansive semigroup in Banach spaces. Fixed Point Theory and Applications 2011, 2011:-17.
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Downing DJ: Surjectivity results for
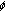 -accretive set-valued mappings. Pacific Journal of Mathematics 1978,77(2):381–388.
-accretive set-valued mappings. Pacific Journal of Mathematics 1978,77(2):381–388.
Author information
Authors and Affiliations
Corresponding author
Additional information
The online version of the original article can be found at10.1155/2011/620284
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mohamadi, I. Erratum to "Iterative Methods for Variational Inequalities over the Intersection of the Fixed Points Set of a Nonexpansive Semigroup in Banach Spaces". Fixed Point Theory Appl 2011, 187439 (2011). https://doi.org/10.1155/2011/187439
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/187439
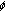 -accretive set-valued mappings. Pacific Journal of Mathematics 1978,77(2):381–388.
-accretive set-valued mappings. Pacific Journal of Mathematics 1978,77(2):381–388.