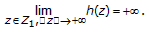- Research Article
- Open access
- Published:
Levitin-Polyak Well-Posedness in Vector Quasivariational Inequality Problems with Functional Constraints
Fixed Point Theory and Applications volume 2010, Article number: 984074 (2010)
Abstract
We introduce several types of Levtin-Polyak well-posedness for a vector quasivariational inequality with functional constraints. Necessary and/or sufficient conditions are derived for them.
1. Introduction
It is well known that, under certain conditions, a Nash equilibrium problem can be formulated and solved as a variational inequality problem. A generalized Nash game is a Nash game in which each player's strategy depends on other players' strategies [1]. The connection between generalized Nash games and quasivariational inequalities was first recognized by Bensoussan [2]. Recently, some researchers [1, 3, 4] found that mathematical models of many real world problems, including some engineering problems, can be formulated as certain kinds of variational inequality problems, including quasivariational inequality problems. However, as noted in [5], compared with variational inequality problems, the study on quasivariational inequality problems is still in its infancy, in particular only a few algorithms have been proposed to solve variational inequalities numerically.
Vector variational inequality problems were introduced by Giannessi [6] and are related to vector network equilibrium problems [7]. Since then, various types of vector variational inequalities were introduced and studied (see, e.g., [8, 9] and the references therein).
In this paper, we will consider vector quasivariational inequality problems with functional constraints, which are described below.
Let  be a normed space and
be a normed space and  a metric space. Let
a metric space. Let  be nonempty and closed sets. Let
be nonempty and closed sets. Let  be a locally convex space and
be a locally convex space and  be a nontrivial closed and convex cone with nonempty interior
be a nontrivial closed and convex cone with nonempty interior  . Define the following order in
. Define the following order in  , for any
, for any  ,
,

Let  be the space of all the linear continuous operators from
be the space of all the linear continuous operators from  to
to  . Let
. Let  and
and  be two functions. We denote by
be two functions. We denote by  the function value
the function value  , where
, where  . Let
. Let  be a strict set-valued map (i.e.,
be a strict set-valued map (i.e.,  ).
).
Let

The vector quasivariational inequality problem with functional and abstract set constraints considered in this paper is:

Denote by  the solution set of (VQVI).
the solution set of (VQVI).
Well-posedness for unconstrained and constrained optimization problems was first studied by Tikhonov [10] and Levitin and Polyak [11]. The issue being considered is that for each approximating solution sequence, there exists a subsequence that converges to a solution of the problem.
In Tikhonov's well posedness, the approximating solution is always feasible. However, it should be noted that many algorithms in optimization and variational inequalities, such as penalty-type methods and augmented Lagrangian methods, terminate when the constraint is approximately satisfied. These methods may generate sequences that may not be necessarily feasible [12].
Up to now, various extensions of these well posednesses have been developed and well studied (see, e.g., [13–18]). Studies on well posedness of optimization problems have been extended to vector optimization problems (see e.g., [19–24]). The study of Levitin-Polyak well posedness for scalar convex optimization problems with functional constraints originates from [25]. Recently, this research was extended to nonconvex optimization problems with abstract and functional constraints [12] and nonconvex vector optimization problems with both abstract and functional constraints [26]. Well-posedness of variational inequality problems, mixed variational inequality problems, and equilibrium problems without functional constraints was investigated in the literature (see, e.g., [27–30]). Well-posedness in variational inequality problems with both abstract and functional constraints was investigated in [31]. Well-posedness of (generalized) quasivariational inequality and mixed quasivariational-like inequalities has been studied in the literature [32–35]. The study of well posedness for (generalized) vector variational inequality, vector quasiequilibria and vector equilibrium problems can be found in [36–39] and the references therein.
In this paper, we will introduce and study several types of Levitin-Polyak (LP in short) well posednesses and generalized LP well posednesses for vector quasivariational inequalities with functional constraints. The paper is organized as follows. In Section 2, four types of LP well posednesses and generalized LP well posednesses for vector quasivariational inequality problems will be defined. In Section 3, we will derive various criteria and characterizations for the various (generalized) LP well posednesses of constrained vector quasivariational inequalities.
2. Definitions and Preliminaries
Let  ,
,  be two normed spaces. A set-valued map
be two normed spaces. A set-valued map  from
from  to
to  is
is
(i)closed, on  , if for any sequence
, if for any sequence  with
with  and
and  with
with  , one has
, one has  ;
;
(ii)lower semicontinuous (l.s.c. in short) at  , if
, if  ,
,  , and
, and  imply that there exists a sequence
imply that there exists a sequence  satisfying
satisfying  such that
such that  for
for  sufficiently large. If
sufficiently large. If  is l.s.c. at each point of
is l.s.c. at each point of  , we say that
, we say that  is l.s.c on
is l.s.c on  .
.
Let  be a metric space,
be a metric space,  , and
, and  . In the sequel, we denote by
. In the sequel, we denote by  the distance function from point
the distance function from point  to set
to set  . For a topological vector space
. For a topological vector space  , we denote by
, we denote by  its dual space. For any cone
its dual space. For any cone  , we will denote the (positive) polar cone of
, we will denote the (positive) polar cone of  by
by

Let  be fixed. Denote
be fixed. Denote

Throughout this paper, we always assume that the feasible set  is nonempty and the function
is nonempty and the function  is continuous on
is continuous on  .
.
Definition 2.1.
-
(i)
A sequence
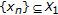 is called a type I Levtin-Polyak (LP in short) approximating solution sequence if there exists
is called a type I Levtin-Polyak (LP in short) approximating solution sequence if there exists 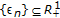 with
with 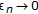 such that
such that 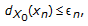 (2.3)
(2.3)


(ii)  is called a type II LP approximating solution sequence if there exist
is called a type II LP approximating solution sequence if there exist  with
with  and
and  with
with  such that (2.3)–(2.5) hold and
such that (2.3)–(2.5) hold and

(iii)  is called a generalized type I LP approximating solution sequence if there exists
is called a generalized type I LP approximating solution sequence if there exists  with
with  such that
such that

and (2.4), (2.5) hold.
-
(iv)
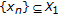 is called a generalized type II LP approximating solution sequence if there exist
is called a generalized type II LP approximating solution sequence if there exist  with
with 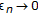 and
and 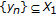 with
with 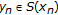 such that (2.4)–(2.7) hold.
such that (2.4)–(2.7) hold.
Definition 2.2.
(VQVI) is said to be type I (resp., type II, generalized type I, generalized type II) LP well posed if the solution set  of (VQVI) is nonempty, and for any type I (resp., type II, generalized type I, generalized type II) LP approximating solution sequence
of (VQVI) is nonempty, and for any type I (resp., type II, generalized type I, generalized type II) LP approximating solution sequence  , there exist a subsequence
, there exist a subsequence  of
of  and
and  such that
such that  .
.
Remark 2.3.
-
(i)
It is easily seen that if
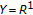 ,
, 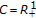 , then type I (resp., type II, generalized type I, generalized type II) LP well posedness of (VQVI) reduces to type I (resp., type II, generalized type I, generalized type II) LP well posedness of (QVI) defined in [34].
, then type I (resp., type II, generalized type I, generalized type II) LP well posedness of (VQVI) reduces to type I (resp., type II, generalized type I, generalized type II) LP well posedness of (QVI) defined in [34]. -
(ii)
It is clear that any (generalized) type II LP approximating solution sequence is a (generalized) type I LP approximating solution sequence. Thus, (generalized) type I LP well posedness implies (generalized) type II LP well posedness.
(iii)Each type of LP well posedness of (VQVI) implies that its solution set  is compact.
is compact.
To see that the various LP well posednesses of (VQVI) are adaptations of the corresponding LP well posednesses in minimizing problems by using the Auslender gap function, we consider the following general constrained optimization problem:

where  is nonempty and
is nonempty and  is proper. The feasible set of (P) is
is proper. The feasible set of (P) is  , where
, where  . The optimal set and optimal value of (P) are denoted by
. The optimal set and optimal value of (P) are denoted by  , respectively. Note that if
, respectively. Note that if  , where
, where

then  . In this paper, we always assume that
. In this paper, we always assume that  . We note that LP well posedness for the special case, where
. We note that LP well posedness for the special case, where  is finite valued and l.s.c.,
is finite valued and l.s.c.,  is closed, has been studied in [12].
is closed, has been studied in [12].
Definition 2.4.
-
(i)
A sequence
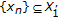 is called a type I LP minimizing sequence for (P) if
is called a type I LP minimizing sequence for (P) if 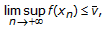 (2.9)
(2.9)

(ii)  is called a type II LP minimizing sequence for (P) if
is called a type II LP minimizing sequence for (P) if

and (2.10) hold.
-
(iii)
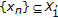 is called a generalized type I LP minimizing sequence for (P) if
is called a generalized type I LP minimizing sequence for (P) if  (2.12)
(2.12)
and (2.9) hold.
-
(iv)
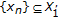 is called a generalized type II LP minimizing sequence for (P) if (2.11) and (2.12) hold.
is called a generalized type II LP minimizing sequence for (P) if (2.11) and (2.12) hold.
Definition 2.5.
-
(P)
is said to be type I (resp., type II, generalized type I, generalized type II) LP well posed if the solution set
 of (P) is nonempty, and for any type I (resp., type II, generalized type I, generalized type II) LP minimizing sequence
of (P) is nonempty, and for any type I (resp., type II, generalized type I, generalized type II) LP minimizing sequence  , there exist a subsequence
, there exist a subsequence 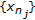 of
of 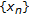 and
and 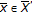 such that
such that 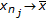 .
.
The Auslender gap function for (VQVI) is

From Lemma  in [40], we know that
in [40], we know that  is weak* compact. This fact combined with that
is weak* compact. This fact combined with that  when
when  implies that
implies that

Recall the following nonlinear scalarization function (see, e.g., [9]):

It is known that  is a continuous, (strictly) monotone (i.e., for any
is a continuous, (strictly) monotone (i.e., for any  ,
,  ,
,  implies that
implies that  and
and  implies that
implies that  ), subadditive, and convex function. Moreover, for any
), subadditive, and convex function. Moreover, for any  , it holds that
, it holds that  . Furthermore, following the proof of [9, Proposition
. Furthermore, following the proof of [9, Proposition  ], we can prove that
], we can prove that

Let  be defined by
be defined by

First we have the following lemma.
Lemma 2.6.
Let  be defined by (2.14), then
be defined by (2.14), then
(i) , for all
, for all  ,
,
(ii) and
and  if and only if
if and only if  .
.
Proof.
-
(i)
Let
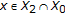 , then
, then 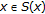 . We let
. We let  in (2.14) be equal to
in (2.14) be equal to  , then
, then 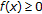 .
. -
(ii)
Assume that
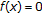 . Suppose to the contrary that
. Suppose to the contrary that  , then, there exists
, then, there exists 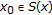 such that
such that  (2.18)
(2.18)
Thus,

It follows that

Hence,  , contradicting the assumption, so
, contradicting the assumption, so  . Conversely, assume that
. Conversely, assume that  , then we have
, then we have

As a result, for any  , there exists
, there exists  such that
such that

It follows that  . This fact combined with (i) implies that
. This fact combined with (i) implies that  .
.
In the rest of this paper, we set  in (P) equal to
in (P) equal to  . Note that if the set-valued map
. Note that if the set-valued map  is closed on
is closed on  , then
, then  is closed. By Lemma 2.6,
is closed. By Lemma 2.6,  if and only if
if and only if  minimizes
minimizes  (defined by (2.26)) over
(defined by (2.26)) over  with
with  .
.
The following lemma establishes some relationship between LP approximating solution sequence and LP minimizing sequence.
Lemma 2.7.
Let the function  be defined by (2.14) as follows:
be defined by (2.14) as follows:
(i) is a sequence such that there exists
is a sequence such that there exists  with
with  satisfying (2.4)-(2.5) if and only if
satisfying (2.4)-(2.5) if and only if  and (2.9) holds with
and (2.9) holds with  .
.
(ii) is a sequence such that there exist
is a sequence such that there exist  with
with  and
and  with
with  satisfying (2.4)–(2.6) if and only if
satisfying (2.4)–(2.6) if and only if  and (2.11) holds with
and (2.11) holds with  .
.
Proof.
-
(i)
Let
 be any sequence, if there exists
be any sequence, if there exists  with
with 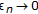 satisfying (2.4)-(2.5), then we can easily verify that
satisfying (2.4)-(2.5), then we can easily verify that  (2.23)
(2.23)
It follows that (2.9) holds with  .
.
For the converse, let  and (2.9) hold. We can see that
and (2.9) hold. We can see that  and (2.4) hold. Furthermore, by (2.9), we have that there exists
and (2.4) hold. Furthermore, by (2.9), we have that there exists

such that

That is,

Now, we will show that (2.5) holds, otherwise there exists  such that
such that

As a result, for any  ,
,  Since
Since  is a weak* compact set, we have
is a weak* compact set, we have

which contradicts (2.26).
-
(ii)
Let
 be any sequence, we can check that
be any sequence, we can check that 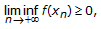 (2.29)
(2.29)
holds if and only if there exists  with
with  and
and  with
with  such that (2.6) (with
such that (2.6) (with  replaced by
replaced by  ) holds. From the proof of (i), we know that
) holds. From the proof of (i), we know that

and  hold if and only if
hold if and only if  such that there exists
such that there exists  with
with  satisfying (2.4)-(2.5) (with
satisfying (2.4)-(2.5) (with  replaced by
replaced by  ). Finally, we set
). Finally, we set  and the conclusion follows.
and the conclusion follows.
The next proposition establishes relationships between the various LP well posednesses of (VQVI) and those of (P) with  defined by (2.14).
defined by (2.14).
Proposition 2.8.
Assume that  , then
, then
(i)(VQVI) is generalized type I (resp., generalized type II) LP well posed if and only if (P) is generalized type I (resp., generalized type II) LP well posed with  defined by (2.14).
defined by (2.14).
(ii)If (VQVI) is type I (resp., type II) LP well posed, (P) is type I (resp., type II) LP well posed with  defined by (2.14).
defined by (2.14).
Proof.
By Lemma 2.6, if  ,
,  is a solution of (VQVI) if and only if
is a solution of (VQVI) if and only if  is an optimal solution of (P) with
is an optimal solution of (P) with  and
and  defined by (2.14).
defined by (2.14).
-
(i)
Similar to the proof of Lemma 2.7, it is also routine to check that a sequence
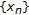 is a generalized type I (resp., generalized type II) LP approximating solution sequence if and only if it is a generalized type I (resp., generalized type II) LP minimizing sequence of (P). So (VQVI) is generalized type I (resp., generalized type II) LP well posed if and only if (P) is generalized type I (resp., generalized type II) LP well posed with
is a generalized type I (resp., generalized type II) LP approximating solution sequence if and only if it is a generalized type I (resp., generalized type II) LP minimizing sequence of (P). So (VQVI) is generalized type I (resp., generalized type II) LP well posed if and only if (P) is generalized type I (resp., generalized type II) LP well posed with  defined by (2.26).
defined by (2.26). -
(ii)
Since
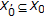 ,
,  for any
for any  . This fact together with Lemma 2.7 implies that a type I (resp., type II) LP minimizing sequence of (P) is a type I (resp., type II) LP approximating solution sequence. So type I (resp., type II) LP well posedness of (VQVI) implies type I (resp., type II) LP well posedness of (P) with
. This fact together with Lemma 2.7 implies that a type I (resp., type II) LP minimizing sequence of (P) is a type I (resp., type II) LP approximating solution sequence. So type I (resp., type II) LP well posedness of (VQVI) implies type I (resp., type II) LP well posedness of (P) with 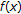 defined by (2.26).
defined by (2.26).
To end this section, we note that all the results in [12] for the well posedness hold for (P) so long as  is closed,
is closed,  is l.s.c. on
is l.s.c. on  , and
, and  .
.
3. Criteria and Characterizations for Various LP Well-Posedness of (VQVI)
In this section, we give necessary and/or sufficient conditions for the various types of (generalized) LP well posednesses defined in Section 2.
Consider the following statement:

The next proposition can be straightforwardly proved.
Proposition 3.1.
If (VQVI) is type I (resp., type II, generalized type I, generalized type II) LP well posed, then (3.1) holds. Conversely, if (3.1) holds and  is compact, then (VQVI) is type I (resp., type II, generalized type I, generalized type II) LP well posed.
is compact, then (VQVI) is type I (resp., type II, generalized type I, generalized type II) LP well posed.
Now, we consider a real-valued function  defined for
defined for  sufficiently small such that
sufficiently small such that

With the help of Lemma 2.7, analogously to [35, Theorems  , and
, and  ], we can prove the following two theorems.
], we can prove the following two theorems.
Theorem 3.2.
If (VQVI) is type II LP well posed, the set-valued map  is closed valued, then there exists a function c satisfying (3.2) such that
is closed valued, then there exists a function c satisfying (3.2) such that

where  is defined by (2.14). Conversely, suppose that
is defined by (2.14). Conversely, suppose that  is nonempty and compact, and (3.3) holds for some
is nonempty and compact, and (3.3) holds for some  satisfying (3.2), then (VQVI) is type II LP well posed.
satisfying (3.2), then (VQVI) is type II LP well posed.
Theorem 3.3.
If (VQVI) is type II LP well posed in the generalized sense, the set-valued mapping  is closed, then there exists a function
is closed, then there exists a function  satisfying (3.2) such that
satisfying (3.2) such that

where  is defined by (2.14). Conversely, suppose that
is defined by (2.14). Conversely, suppose that  is nonempty and compact, and (3.4) holds for some
is nonempty and compact, and (3.4) holds for some  satisfying (3.2), then (VQVI) is generalized type II LP well posed.
satisfying (3.2), then (VQVI) is generalized type II LP well posed.
Next we give Furi-Vignoli type characterizations [41] for the (generalized) type I LP well posednesses of (VQVI).
Let  be a Banach space. Recall that the Kuratowski measure of noncompactness for a subset
be a Banach space. Recall that the Kuratowski measure of noncompactness for a subset  of
of  is defined as
is defined as

where diam is the diameter of
is the diameter of  defined by
defined by

For any  , define
, define

Lemma 3.4.
Let  be defined by (2.14) and
be defined by (2.14) and  . Let
. Let


then one has  and
and  .
.
Proof.
First, we prove the former result. For any  satisfying
satisfying

we have  and
and  . We will show that
. We will show that  , for all
, for all  . Otherwise, there exists
. Otherwise, there exists  such that
such that  . By the weak* compactness of
. By the weak* compactness of  , we have
, we have  , which leads to
, which leads to  and gives rise to a contradiction. Furthermore, we observe that
and gives rise to a contradiction. Furthermore, we observe that  . This fact combined with
. This fact combined with  implies that
implies that  .
.
Now, we prove the equivalence between  and
and  . Firstly, we can establish the same inclusion for
. Firstly, we can establish the same inclusion for  and
and  analogously to the proof stated above. Then if
analogously to the proof stated above. Then if  satisfies
satisfies  and
and

It is routine to check that  . From (3.11), we know that for each
. From (3.11), we know that for each  , there exists
, there exists  such that
such that  . As a result, we can see that
. As a result, we can see that  . Thus, we prove the conclusion.
. Thus, we prove the conclusion.
The next lemma can be proved analogously to ([25, Theorem  ]).
]).
Lemma 3.5.
Let  be a Banach space. Suppose that
be a Banach space. Suppose that  is l.s.c. on
is l.s.c. on  and bounded below on
and bounded below on  . Assume that the optimal solution set of (P) is nonempty and compact, then, (P) is (generalized) type I LP well posed if and only if
. Assume that the optimal solution set of (P) is nonempty and compact, then, (P) is (generalized) type I LP well posed if and only if

To continue our study, we make some assumptions below.
Assumption.
-
(i)
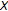 is a Banach space.
is a Banach space. -
(ii)
The set-valued map
 is closed, and lower semicontinuous on
is closed, and lower semicontinuous on 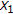 .
. -
(iii)
The map
 is continuous on
is continuous on  .
.
We have the following lemma concerning the l.s.c. of  defined by (2.14).
defined by (2.14).
Lemma 3.6.
Let function  be defined by (2.14) and Assumption 1 hold, then
be defined by (2.14) and Assumption 1 hold, then  is l.s.c. function from
is l.s.c. function from  to
to  . Further assume that the solution set
. Further assume that the solution set  of (VQVI) is nonempty, then
of (VQVI) is nonempty, then  .
.
Proof.
First we show that  , for all
, for all  . Suppose to the contrary that there exists
. Suppose to the contrary that there exists  such that
such that  , then,
, then,

That is,

Namely,

which is impossible since  is a finite function on
is a finite function on  . Second, we show that
. Second, we show that  is l.s.c. on
is l.s.c. on  . Note that the function
. Note that the function

is continuous on  by the continuity of
by the continuity of  on
on  and the continuity of
and the continuity of  . We also note that
. We also note that  . Let
. Let  . Suppose that the sequence
. Suppose that the sequence  satisfies
satisfies

and  . For any
. For any  , by the lower semicontinuity of
, by the lower semicontinuity of  and continuity of
and continuity of  , we have a sequence
, we have a sequence  with
with  converging to
converging to  such that
such that

It follows that  . Hence,
. Hence,  is l.s.c. on
is l.s.c. on  . Furthermore, if
. Furthermore, if  , by Lemma 2.6, we see that
, by Lemma 2.6, we see that  .
.
Theorem 3.7.
Let Assumption 1 hold and let the solution set  of (QVVI) be nonempty and compact, then, (VQVI) is generalized type I LP well posed if and only if
of (QVVI) be nonempty and compact, then, (VQVI) is generalized type I LP well posed if and only if

Proof.
Note that the function  defined by (2.14) is nonnegative on
defined by (2.14) is nonnegative on  . By the lower semicontinuity of
. By the lower semicontinuity of  and Lemma 3.6,
and Lemma 3.6,  is l.s.c. on
is l.s.c. on  . Moreover,
. Moreover,  is closed, since
is closed, since  is closed on
is closed on  . By Proposition 2.8, Lemmas 3.4 and 3.5, the conclusion follows.
. By Proposition 2.8, Lemmas 3.4 and 3.5, the conclusion follows.
Although the type I (type II) LP well posedness of (VQVI) is not equivalent to the type I (type II) LP well posedness of (P), we can still establish the same characterization for type I (type II) LP well posedness of (VQVI) as Theorem 3.7. We need the next lemma.
Lemma 3.8.
Let Assumption 1 hold, then  defined by (3.8) is closed.
defined by (3.8) is closed.
Proof.
Let  and
and  . We show that
. We show that  . It is obvious that
. It is obvious that  . Since
. Since  and
and  , by the closedness of
, by the closedness of  , we have
, we have  . Moreover, since
. Moreover, since

hold and  is l.s.c., for any
is l.s.c., for any  , we can find that
, we can find that  with
with  such that
such that

Hence,  is closed.
is closed.
Theorem 3.9.
Let Assumption 1 hold and let  be defined by (2.14). Assume that the solution set
be defined by (2.14). Assume that the solution set  of (QVVI) is nonempty and compact, then (VQVI) is type I LP well posed if and only if
of (QVVI) is nonempty and compact, then (VQVI) is type I LP well posed if and only if

Proof.
The proof is similar to that of Theorem  in [35] and thus omitted.
in [35] and thus omitted.
Example 3.10.
-
(i)
Let
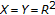 ,
, 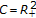 ,
, 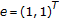 ,
, 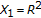 , and
, and 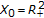 .
. 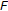 maps
maps 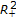 into an identical mapping, that is to say
into an identical mapping, that is to say 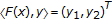 , for any
, for any 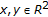 . The set valued mapping
. The set valued mapping 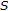 is defined as follows, given
is defined as follows, given 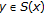 for some
for some 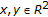 , then
, then 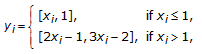 (3.23)
(3.23)
with  , of course
, of course  is closed and l.s.c. Now, we can show that, when
is closed and l.s.c. Now, we can show that, when  ,
,  , which is bounded. Thus,
, which is bounded. Thus,  , by applying Theorem 3.9, we know that (VQVI) is type I LP well posed.
, by applying Theorem 3.9, we know that (VQVI) is type I LP well posed.
(i)Suppose that  is a set-valued mapping from
is a set-valued mapping from  to
to  , for fixed
, for fixed  ,
,  implies that
implies that

with  , obviously
, obviously  is still closed and l.s.c. If we replace
is still closed and l.s.c. If we replace  by
by  in (i), then
in (i), then  with
with  , which is unbounded. Therefore,
, which is unbounded. Therefore,  and the (VQVI) is not LP well posed in sense of type I. Actually, the solution set of this problem is
and the (VQVI) is not LP well posed in sense of type I. Actually, the solution set of this problem is  and thus unbounded.
and thus unbounded.
Definition 3.11.
-
(i)
Let
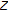 be a topological space, and let
be a topological space, and let 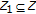 be nonempty. Suppose that
be nonempty. Suppose that 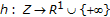 is an extended real-valued function.
is an extended real-valued function. 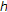 is said to be level compact on
is said to be level compact on 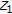 if, for any
if, for any 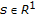 , the subset
, the subset  is compact.
is compact. -
(ii)
Let
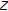 be a finite dimensional normed space, and let
be a finite dimensional normed space, and let 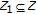 be nonempty. A function
be nonempty. A function 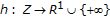 is said to be level bounded on
is said to be level bounded on 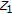 if
if  is bounded or
is bounded or 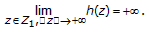 (3.25)
(3.25)
The following proposition presents some sufficient conditions for type I LP well posedness of (VQVI)
Proposition 3.12.
Let Assumption 1 hold. Further assume that one of the following conditions holds.
(i)There exists  such that
such that  is compact, where
is compact, where

(ii)the function  defined by (2.14) is level compact on
defined by (2.14) is level compact on  ,
,
(iii) is finite dimensional and
is finite dimensional and

where  is defined by (2.14).
is defined by (2.14).
(iv)There exists  such that
such that  is level-compact on
is level-compact on  defined by (3.26). Then, (VQVI) is type I LP well posed.
defined by (3.26). Then, (VQVI) is type I LP well posed.
Proof.
First, we show that each one of (i), (ii), and (iii) implies (iv). Clearly, either of (i) and (ii) implies (iv). Now, we show that (iii) implies (iv). We notice that the set  is closed by the closedness of
is closed by the closedness of  . Then, we need only to show that for any
. Then, we need only to show that for any  , the set
, the set

is bounded since  is a finite dimensional space and the function
is a finite dimensional space and the function  defined by (2.14) is l.s.c. on
defined by (2.14) is l.s.c. on  and, thus,
and, thus,  is closed. Suppose to the contrary that there exist
is closed. Suppose to the contrary that there exist  and
and  such that
such that  and
and  . From
. From  , we have
, we have

Thus,

which contradicts condition (3.27).
Now, we show that if (iv) holds, then (VQVI) is type I LP well posed. Let  be a type I LP approximating solution sequence of (VQVI). Then, there exist
be a type I LP approximating solution sequence of (VQVI). Then, there exist  with
with  and
and  such that
such that



From (3.32) and (3.33), we can assume without loss of generality that  . By Lemma 2.7, we can assume without loss of generality that
. By Lemma 2.7, we can assume without loss of generality that

where  is defined by (2.14). By the level compactness of
is defined by (2.14). By the level compactness of  on
on  , there exist a subsequence of
, there exist a subsequence of  of
of  and
and  such that
such that  . From this fact and (3.32), we have
. From this fact and (3.32), we have  . Since
. Since  is closed and (3.33) holds, we also have
is closed and (3.33) holds, we also have  . That is,
. That is,

Furthermore, by Lemmas 2.7 and 3.6, we have

We know that  by Lemma 2.6, so
by Lemma 2.6, so  . This fact combined with (3.35) and Lemma 2.6 implies that
. This fact combined with (3.35) and Lemma 2.6 implies that  .
.
Similarly, we can prove the next proposition.
Proposition 3.13.
Let Assumption 1 hold. Further assume that one of the following conditions holds.
(i)There exists  such that
such that  is compact, where
is compact, where

(ii)the function  defined by (2.14) is level compact on
defined by (2.14) is level compact on  ,
,
(iii) is finite dimensional and
is finite dimensional and

(iv)There exists  such that
such that  is level compact on
is level compact on  defined by (3.37). Then, (VQVI) is generalized type I LP well posed.
defined by (3.37). Then, (VQVI) is generalized type I LP well posed.
Remark 3.14.
If  is finite dimensional, then the "level-compactness" condition in Propositions 3.12 and 3.13 can be replaced by the "level-boundedness" condition.
is finite dimensional, then the "level-compactness" condition in Propositions 3.12 and 3.13 can be replaced by the "level-boundedness" condition.
Now, we consider the case when  is a normed space,
is a normed space,  is a closed and convex cone with nonempty interior
is a closed and convex cone with nonempty interior  and let
and let  .
.
Let  and denote
and denote

The next proposition follows immediately from Proposition 2.8(i), Lemma 3.6, and [12, Proposition  (iv)].
(iv)].
Proposition 3.15.
Let  be a normed space, let
be a normed space, let  be a closed and convex cone with nonempty interior
be a closed and convex cone with nonempty interior  and
and  . Let the set-valued map
. Let the set-valued map  be closed and l.s.c on
be closed and l.s.c on  . Assume that the solution set
. Assume that the solution set  of (VQVI) is nonempty. Further assume that there exists
of (VQVI) is nonempty. Further assume that there exists  such that the function
such that the function  defined by (2.14) is level compact on
defined by (2.14) is level compact on  , then (VQVI) is generalized type I LP well posed.
, then (VQVI) is generalized type I LP well posed.
Remark 3.16.
If  is finite dimensional, then the level-compactness condition of
is finite dimensional, then the level-compactness condition of  can be replaced by the level boundedness of
can be replaced by the level boundedness of  .
.
References
Facchinei F, Pang J-S: Finite-Dimensional Variational Inequalities and Complementarity Problems, Springer Series in Operations Research. Volume 1–2. Springer, New York, NY, USA; 2003:xxxiv+624+I69.
Bensoussan A: Points de nash dans le cas de fonctionnelles quadratiques et jeux différentiels linéaires à personnes. SIAM Journal on Control and Optimization 1974, 12: 460–499. 10.1137/0312037
Pang J-S, Fukushima M: Quasi-variational inequalities, generalized Nash equilibria, and multi-leader-follower games. Computational Management Science 2005,2(1):21–56. 10.1007/s10287-004-0010-0
Baiocchi C, Capelo A: Variational and Quasivariational Inequalities, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1984:ix+452.
Fukushima M: A class of gap functions for quasi-variational inequality problems. Journal of Industrial and Management Optimization 2007,3(2):165–171.
Giannessi F: Theorems of alternative, quadratic programs and complementarity problems. In Variational Inequalities and Complementarity Problems. Edited by: Cottle RW, Giannessi F, Lions JL. John Wiley & Sons, New York, NY, USA; 1980:151–186.
Chen GY, Yen ND: On the variational inequality model for network equilibrium. In Internal Report. Department of Mathematics, University of Pisa, Pisa, Italy; 1993.
Ceng LC, Chen GY, Huang XX, Yao J-C: Existence theorems for generalized vector variational inequalities with pseudomonotonicity and their applications. Taiwanese Journal of Mathematics 2008,12(1):151–172.
Chen GY, Huang XX, Yang XQ: Vector Optimization, Set-Valued and Variational Analysis, Lecture Notes in Economics and Mathematical Systems. Volume 541. Springe, Berlin, Germany; 2005:x+306.
Tikhonov AN: On the stability of the functional optimization problem. USSR Computational Mathematics and Mathematical Physics 1966,6(4):28–33. 10.1016/0041-5553(66)90003-6
Levitin ES, Polyak BT: Convergence of minimizing sequences in conditional extremum problems. Soviet Mathematics Doklady 1966, 7: 764–767.
Huang XX, Yang XQ: Generalized Levitin-Polyak well-posedness in constrained optimization. SIAM Journal on Optimization 2006,17(1):243–258. 10.1137/040614943
Beer G, Lucchetti R: The epi-distance topology: continuity and stability results with applications to convex optimization problems. Mathematics of Operations Research 1992,17(3):715–726. 10.1287/moor.17.3.715
Dontchev AL, Zolezzi T: Well-Posed Optimization Problems, Lecture Notes in Mathematics. Volume 1543. Springer, Berlin, Germany; 1993:xii+421.
Revalski JP: Hadamard and strong well-posedness for convex programs. SIAM Journal on Optimization 1997,7(2):519–526. 10.1137/S1052623495286776
Lucchetti R, Revalski J (Eds): Recent Developments in Well-Posed Variational Problems, Mathematics and its Applications. Volume 331. Kluwer Academic, Dodrecht, The Netherlands; 1995:viii+266.
Zolezzi T: Well-posedness criteria in optimization with application to the calculus of variations. Nonlinear Analysis: Theory, Methods & Applications 1995,25(5):437–453. 10.1016/0362-546X(94)00142-5
Zolezzi T: Extended well-posedness of optimization problems. Journal of Optimization Theory and Applications 1996,91(1):257–266. 10.1007/BF02192292
Bednarczuk E: Well-posedness of vector optimization problems. In Recent Advances and Historical Development of Vector Optimization Problems, Lecture Notes in Economics and Mathematical Systems. Volume 294. Edited by: Jahn J, Krabs W. Springer, Berlin, Germany; 1987:51–61.
Deng S: Coercivity properties and well-posedness in vector optimization. RAIRO Operations Research 2003,37(3):195–208. 10.1051/ro:2003021
Huang XX: Extended well-posedness properties of vector optimization problems. Journal of Optimization Theory and Applications 2000,106(1):165–182. 10.1023/A:1004615325743
Huang XX: Extended and strongly extended well-posedness of set-valued optimization problems. Mathematical Methods of Operations Research 2001,53(1):101–116. 10.1007/s001860000100
Loridan P: Well-posedness in vector optimization. In Recent Developments in Well-Posed Variational Problems, Mathematics and Its Applications. Volume 331. Kluwer Academic, Dodrecht, The Netherlands; 1995:171–192.
Lucchetti R: Well-Posedness Towards Vector Optimization, Lecture Notes in Economics and Mathematical System. Volume 294. Springer, New York, NY, USA; 1987.
Konsulova AS, Revalski JP: Constrained convex optimization problems-well-posedness and stability. Numerical Functional Analysis and Optimization 1994,15(7–8):889–907. 10.1080/01630569408816598
Huang XX, Yang XQ: Levitin-Polyak well-posedness of constrained vector optimization problems. Journal of Global Optimization 2007,37(2):287–304. 10.1007/s10898-006-9050-z
Fang Y-P, Huang N-J, Yao J-C: Well-posedness of mixed variational inequalities, inclusion problems and fixed point problems. Journal of Global Optimization 2008,41(1):117–133. 10.1007/s10898-007-9169-6
Fang Y-P, Huang N-J, Yao J-C: Well-posedness by perturbations of mixed variational inequalities in Banach spaces. European Journal of Operational Research 2010,201(3):682–692. 10.1016/j.ejor.2009.04.001
Lignola MB, Morgan J: -well-posedness for Nash equilibria and for optimization problems with Nash equilibrium constraints. Journal of Global Optimization 2006,36(3):439–459. 10.1007/s10898-006-9020-5
Lignola MB, Morgan J: Generalized variational inequalities with pseudomonotone operators under perturbations. Journal of Optimization Theory and Applications 1999,101(1):213–220. 10.1023/A:1021783313936
Huang XX, Yang XQ, Zhu DL: Levitin-Polyak well-posedness of variational inequality problems with functional constraints. Journal of Global Optimization 2009,44(2):159–174. 10.1007/s10898-008-9310-1
Ceng LC, Hadjisavvas N, Schaible S, Yao JC: Well-posedness for mixed quasivariational-like inequalities. Journal of Optimization Theory and Applications 2008,139(1):109–125. 10.1007/s10957-008-9428-9
Lignola MB: Well-posedness and -well-posedness for quasivariational inequalities. Journal of Optimization Theory and Applications 2006,128(1):119–138. 10.1007/s10957-005-7561-2
Huang XX, Jiang B, Zhang J: Levitin-Polyak well-posedness of quasivariational inequality problems with functional constraints. Natural Science Jourmal of Xiangtan University 2008, 30: 1–11.
Jiang B, Zhang J, Huang XX: Levitin-Polyak well-posedness of generalized quasivariational inequalities with functional constraints. Nonlinear Analysis: Theory, Methods & Applications 2009,70(4):1492–1503. 10.1016/j.na.2008.02.029
Anh LQ, Khanh PQ, Van DTM, Yao J-C: Well-posedness for vector quasiequilibria. Taiwanese Journal of Mathematics 2009,13(2):713–737.
Huang XX, Yang XQ: Levitin-Polyak well-posedness of vector variational inequality problems with functional constraints. Numerical Functional Analysis and Optimization 2010,31(4):440–459. 10.1080/01630563.2010.485296
Li SJ, Li MH: Levitin-Polyak well-posedness of vector equilibrium problems. Mathematical Methods of Operations Research 2009,69(1):125–140. 10.1007/s00186-008-0214-0
Wang G, Huang XX, Zhang J, Chen GY: Levitin-Polyak well-posedness for vector equilibrium problems with functional constraints. Acta Mathematica Scientia 2010,30(5):1400–1412. 10.1016/S0252-9602(10)60132-4
Huang XX, Teo KL, Yang XQ: Calmness and exact penalization in vector optimization with cone constraints. Computational Optimization and Applications 2006,35(1):47–67. 10.1007/s10589-006-6441-5
Furi M, Vignoli A: About well-posed minimization problems for functionals in metric spaces. Journal of Optimization Theory and Applications 1970, 5: 225–229. 10.1007/BF00927717
Acknowledgment
This work is supported by the National Science Foundation of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, J., Jiang, B. & Huang, X. Levitin-Polyak Well-Posedness in Vector Quasivariational Inequality Problems with Functional Constraints. Fixed Point Theory Appl 2010, 984074 (2010). https://doi.org/10.1155/2010/984074
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/984074
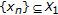 is called a type I Levtin-Polyak (LP in short) approximating solution sequence if there exists
is called a type I Levtin-Polyak (LP in short) approximating solution sequence if there exists 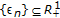 with
with 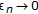 such that
such that 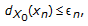
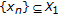 is called a generalized type II LP approximating solution sequence if there exist
is called a generalized type II LP approximating solution sequence if there exist  with
with 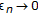 and
and 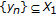 with
with 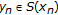 such that (2.4)–(2.7) hold.
such that (2.4)–(2.7) hold.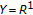 ,
, 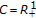 , then type I (resp., type II, generalized type I, generalized type II) LP well posedness of (VQVI) reduces to type I (resp., type II, generalized type I, generalized type II) LP well posedness of (QVI) defined in [
, then type I (resp., type II, generalized type I, generalized type II) LP well posedness of (VQVI) reduces to type I (resp., type II, generalized type I, generalized type II) LP well posedness of (QVI) defined in [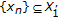 is called a type I LP minimizing sequence for (P) if
is called a type I LP minimizing sequence for (P) if 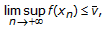
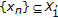 is called a generalized type I LP minimizing sequence for (P) if
is called a generalized type I LP minimizing sequence for (P) if 
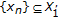 is called a generalized type II LP minimizing sequence for (P) if (2.11) and (2.12) hold.
is called a generalized type II LP minimizing sequence for (P) if (2.11) and (2.12) hold. of (P) is nonempty, and for any type I (resp., type II, generalized type I, generalized type II) LP minimizing sequence
of (P) is nonempty, and for any type I (resp., type II, generalized type I, generalized type II) LP minimizing sequence  , there exist a subsequence
, there exist a subsequence 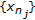 of
of 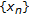 and
and 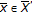 such that
such that 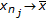 .
.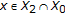 , then
, then 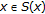 . We let
. We let  in (2.14) be equal to
in (2.14) be equal to  , then
, then 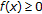 .
.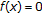 . Suppose to the contrary that
. Suppose to the contrary that  , then, there exists
, then, there exists 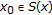 such that
such that 
 be any sequence, if there exists
be any sequence, if there exists  with
with 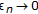 satisfying (2.4)-(2.5), then we can easily verify that
satisfying (2.4)-(2.5), then we can easily verify that 
 be any sequence, we can check that
be any sequence, we can check that 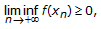
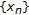 is a generalized type I (resp., generalized type II) LP approximating solution sequence if and only if it is a generalized type I (resp., generalized type II) LP minimizing sequence of (P). So (VQVI) is generalized type I (resp., generalized type II) LP well posed if and only if (P) is generalized type I (resp., generalized type II) LP well posed with
is a generalized type I (resp., generalized type II) LP approximating solution sequence if and only if it is a generalized type I (resp., generalized type II) LP minimizing sequence of (P). So (VQVI) is generalized type I (resp., generalized type II) LP well posed if and only if (P) is generalized type I (resp., generalized type II) LP well posed with  defined by (2.26).
defined by (2.26).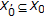 ,
,  for any
for any  . This fact together with Lemma 2.7 implies that a type I (resp., type II) LP minimizing sequence of (P) is a type I (resp., type II) LP approximating solution sequence. So type I (resp., type II) LP well posedness of (VQVI) implies type I (resp., type II) LP well posedness of (P) with
. This fact together with Lemma 2.7 implies that a type I (resp., type II) LP minimizing sequence of (P) is a type I (resp., type II) LP approximating solution sequence. So type I (resp., type II) LP well posedness of (VQVI) implies type I (resp., type II) LP well posedness of (P) with 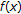 defined by (2.26).
defined by (2.26).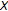 is a Banach space.
is a Banach space. is closed, and lower semicontinuous on
is closed, and lower semicontinuous on 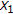 .
. is continuous on
is continuous on  .
.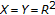 ,
, 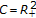 ,
, 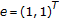 ,
, 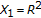 , and
, and 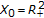 .
. 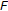 maps
maps 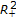 into an identical mapping, that is to say
into an identical mapping, that is to say 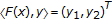 , for any
, for any 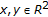 . The set valued mapping
. The set valued mapping 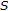 is defined as follows, given
is defined as follows, given 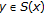 for some
for some 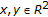 , then
, then 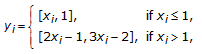
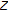 be a topological space, and let
be a topological space, and let 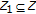 be nonempty. Suppose that
be nonempty. Suppose that 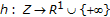 is an extended real-valued function.
is an extended real-valued function. 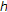 is said to be level compact on
is said to be level compact on 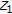 if, for any
if, for any 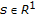 , the subset
, the subset  is compact.
is compact.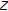 be a finite dimensional normed space, and let
be a finite dimensional normed space, and let 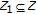 be nonempty. A function
be nonempty. A function 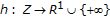 is said to be level bounded on
is said to be level bounded on 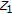 if
if  is bounded or
is bounded or