- Research Article
- Open access
- Published:
Stable Iteration Procedures in Metric Spaces which Generalize a Picard-Type Iteration
Fixed Point Theory and Applications volume 2010, Article number: 953091 (2010)
Abstract
This paper investigates the stability of iteration procedures defined by continuous functions acting on self-maps in continuous metric spaces. Some of the obtained results extend the contraction principle to the use of altering-distance functions and extended altering-distance functions, the last ones being piecewise continuous. The conditions for the maps to be contractive for the achievement of stability of the iteration process can be relaxed to the fulfilment of being large contractions or to be subject to altering-distance functions or extended altering functions.
1. Introduction
Banach contraction principle is a very basic and useful result of Mathematical Analysis [1–7]. Basic applications of this principle are related to stability of both continuous-time and discrete-time dynamic systems [4, 8], including the case of high-complexity models for dynamic systems consisting of functional differential equations by the presence of delays [4, 9]. Several generalizations of the contraction principle are investigated in [2] by proving that the result still holds if altering-distance functions [1] are replaced with a difference of two continuous monotone nondecreasing real functions which take zero values only at the origin. The so-called  -times reasonable expansive mappings and the associated existence of unique fixed points are investigated in [7]. The so-called Halpern's iteration [10] and several of its extensions in the context of fixed-point theory have been investigated in [11–13]. Further extended viscosity iteration schemes with nonexpansive mappings based on the above one have been investigated in [9, 10, 12–18], while proving the common existence of unique fixed points for the related schemes and the strong convergence of the iterations to those points for any arbitrary initial conditions. The stability of Picard iteration has been investigated exhaustively (see, e.g., [5, 19–22]). The Picard and approximate Picard methods have been also used in classical papers for proving the existence and uniqueness of solutions in many differential equations including those of Sobolev type (see, e.g., [23]).
-times reasonable expansive mappings and the associated existence of unique fixed points are investigated in [7]. The so-called Halpern's iteration [10] and several of its extensions in the context of fixed-point theory have been investigated in [11–13]. Further extended viscosity iteration schemes with nonexpansive mappings based on the above one have been investigated in [9, 10, 12–18], while proving the common existence of unique fixed points for the related schemes and the strong convergence of the iterations to those points for any arbitrary initial conditions. The stability of Picard iteration has been investigated exhaustively (see, e.g., [5, 19–22]). The Picard and approximate Picard methods have been also used in classical papers for proving the existence and uniqueness of solutions in many differential equations including those of Sobolev type (see, e.g., [23]).
This paper presents some generalizations of results concerning the stability of iterations in the sense that the iteration scheme subject to error sequences converges asymptotically to its nominal fixed point provided that the iteration error converges asymptotically to zero. Several generalizations are discussed in the framework of stability of iteration schemes in complete metric spaces including:
(a)the use of altering-distance functions (Definition 1.1) [1, 2], and the so-called then defined extended altering functions (Definition 2.1 in Section 2) where the continuous altering functions are allowed to be piecewise continuous;
(b)the use of iteration schemes which are based on continuous functions which modify the Picard iteration scheme [5, 6];
(c)the removal of the common hypothesis in the context of  -stability that the set of fixed points of the iteration scheme is nonempty by guaranteeing that this is in fact true under contractive mappings, large contractions, or altering- and extended altering-distance functions, [1–4, 6].
-stability that the set of fixed points of the iteration scheme is nonempty by guaranteeing that this is in fact true under contractive mappings, large contractions, or altering- and extended altering-distance functions, [1–4, 6].
Definition 1.1 (see [1] (altering-distance function)).
A monotone nondecreasing function  , with
, with  , if and only if
, if and only if  , is said to be an altering-distance function.
, is said to be an altering-distance function.
If  is a complete metric space,
is a complete metric space,  is a self-mapping on
is a self-mapping on  , and
, and  , for all
, for all  and some real constant
and some real constant  , then
, then  has a unique fixed point [1, 2]. This result is extendable to the use of monotone nondecreasing functions
has a unique fixed point [1, 2]. This result is extendable to the use of monotone nondecreasing functions  satisfying
satisfying

for some monotone nondecreasing function  satisfying
satisfying  . Those results are directly extended to monotone nondecreasing piecewise continuous functions being continuous at "0" after a preliminary "ad hoc" definition in the subsequent section.
. Those results are directly extended to monotone nondecreasing piecewise continuous functions being continuous at "0" after a preliminary "ad hoc" definition in the subsequent section.
2. Fixed Point Properties Related to Altering- and Extended Altering-Distance Functions
Since  but continuous at
but continuous at  it can possess bounded isolated discontinuities on
it can possess bounded isolated discontinuities on  and it is necessary to reflect this fact in the notation as follows. The left (resp., right) limit of
and it is necessary to reflect this fact in the notation as follows. The left (resp., right) limit of  at
at  is simply denoted by
is simply denoted by  , instead of using the more cumbersome classical notation
, instead of using the more cumbersome classical notation  (resp., by
(resp., by  instead of using the more cumbersome
instead of using the more cumbersome  ). Since
). Since  is an extended altering-distance function, then continuous at
is an extended altering-distance function, then continuous at  ,
,  . If
. If  is continuous at a given
is continuous at a given  , then
, then  . If
. If  is has a discontinuity point (of second class), then
is has a discontinuity point (of second class), then  , with
, with  .
.
Definition 2.1 (extended altering-distance function).
A monotone nondecreasing function  being continuous at "0", with
being continuous at "0", with  , if and only if
, if and only if  , is said to be an extended altering-distance function.
, is said to be an extended altering-distance function.
Theorem 2.2.
Let  be a complete metric space and
be a complete metric space and  be a self-mapping on
be a self-mapping on  . Then, the following properties hold.
. Then, the following properties hold.
(i)Assume that  is an altering-distance function such that
is an altering-distance function such that  , for all
, for all  for some real constant
for some real constant  . Then
. Then  has a unique fixed point [1].
has a unique fixed point [1].
(ii)Assume that  is an extended altering-distance function such that
is an extended altering-distance function such that  and
and  , for all
, for all  for some real function
for some real function

defined by

for all  for some monotone nondecreasing function
for some monotone nondecreasing function  satisfying
satisfying  , for all
, for all  and
and  , if and only if
, if and only if  Then
Then  is monotone nondecreasing and
is monotone nondecreasing and  has a unique fixed point. In particular, if
has a unique fixed point. In particular, if  so that
so that

for all  for some monotone nondecreasing function
for some monotone nondecreasing function  satisfying
satisfying  for all
for all  and
and  , if and only if
, if and only if  , then
, then  has a unique fixed point.
has a unique fixed point.
Proof.
Note that  from l'Hopital rule and the fact that both functions
from l'Hopital rule and the fact that both functions  and
and  are continuous at "0" with
are continuous at "0" with  . Note that after taking left and right limits at each nonnegative real argument
. Note that after taking left and right limits at each nonnegative real argument

for all  , such that
, such that  , since
, since

Then,  is monotone nondecreasing from simple inspection of the above properties. Thus,
is monotone nondecreasing from simple inspection of the above properties. Thus,

so that

Now, it is proven by contradiction that there is no  such that
such that  , for any given
, for any given  Take two arbitrary
Take two arbitrary  Assume that
Assume that  , for all
, for all  , and some given
, and some given  , so that if
, so that if  also for all
also for all  , then for some
, then for some  ,
,

for all  But, it always exist a finite
But, it always exist a finite  such that
such that  , for all
, for all  since
since  ;
;  , what leads to a contradiction. Thus, there is no
, what leads to a contradiction. Thus, there is no  such that
such that  , for all
, for all  for any given
for any given  . As a result, the subsequent relations are true:
. As a result, the subsequent relations are true:

for all  , with the above limits since
, with the above limits since  is continuous at
is continuous at  and
and  , if and only if
, if and only if  . Furthermore, any sequence
. Furthermore, any sequence  with
with  , for all
, for all  , is a Cauchy sequence since for any arbitrarily small prefixed constant
, is a Cauchy sequence since for any arbitrarily small prefixed constant  , there exist sequences
, there exist sequences  ,
,  , and
, and  of nonnegative integers satisfying
of nonnegative integers satisfying  ;
;  , such that
, such that

Thus, there is a unique  which is in
which is in  , the set of fixed points of
, the set of fixed points of  , that is,
, that is,  , for all
, for all  . Since
. Since  is a complete metric space and the sequence
is a complete metric space and the sequence  with
with  is a Cauchy sequence, for all
is a Cauchy sequence, for all  then
then  . It holds trivially that all the above proof also holds for special case
. It holds trivially that all the above proof also holds for special case  and some monotone nondecreasing function
and some monotone nondecreasing function  satisfying
satisfying  (i.e.,
(i.e.,  is a weak contraction) as may be proven [3] (see also [24]). Property (ii) has been fully proven.
is a weak contraction) as may be proven [3] (see also [24]). Property (ii) has been fully proven.
Theorem 2.2 might be linked to the concept of large contraction which is less restrictive than that of contraction. The related discussion follows.
Definition 2.3 (see [4] (large contraction)).
Let  be a complete metric space. Then, the self-mapping
be a complete metric space. Then, the self-mapping  on
on  is said to be a large contraction, if
is said to be a large contraction, if  , for all
, for all  , and if for any given
, and if for any given  , such that
, such that  , then there exist
, then there exist  , such that
, such that  .
.
It turns out that a contraction is also a large contraction with  being independent of
being independent of  in Definition 2.3. The following result proves that the self-mapping
in Definition 2.3. The following result proves that the self-mapping  on
on  satisfying Theorem 2.2(ii) is a large contraction.
satisfying Theorem 2.2(ii) is a large contraction.
Proposition 2.4.
Let  be a complete metric space and
be a complete metric space and  be a self-mapping on
be a self-mapping on  . If
. If  is a modified altering-distance function which satisfies the conditions of Theorem 2.2(ii), then
is a modified altering-distance function which satisfies the conditions of Theorem 2.2(ii), then  is a large contraction.
is a large contraction.
Proof.
Given  , for all
, for all  , since
, since  if
if  . Since
. Since  is an extended altering-distance function it is monotone nondecreasing of nonnegative values and taking the zero value only at "0". Thus,
is an extended altering-distance function it is monotone nondecreasing of nonnegative values and taking the zero value only at "0". Thus,  . Furthermore, it is proven by contradiction that for any given
. Furthermore, it is proven by contradiction that for any given  , such that
, such that  ,
,  , such that
, such that  . Take
. Take  , such that
, such that  , and assume that
, and assume that  Since
Since  is monotone nondecreasing, then
is monotone nondecreasing, then  , for all
, for all  , and one also gets that
, and one also gets that

Then,

which are two contradictions. Thus,  , for some
, for some  and
and  is a large contraction.
is a large contraction.
It is now proven that the sequence  is uniformly bounded if Theorem 2.2(ii) holds.
is uniformly bounded if Theorem 2.2(ii) holds.
Proposition 2.5.
Let  be a complete metric space and
be a complete metric space and  be a self-mapping on
be a self-mapping on  . If
. If  is a modified altering-distance function which satisfies the conditions of Theorem 2.2(ii), then
is a modified altering-distance function which satisfies the conditions of Theorem 2.2(ii), then  , for all
, for all  and
and  .
.
Proof.
Proceed by contradiction by assuming that  , for all
, for all  and
and  , is false so that
, is false so that  ,
,  is unbounded. Thus, there is a subsequence
is unbounded. Thus, there is a subsequence  of self-mappings on
of self-mappings on  , with
, with  , as
, as  , such that the real subsequence
, such that the real subsequence  is strictly monotone increasing so that it diverges to
is strictly monotone increasing so that it diverges to  , so that
, so that  and
and  , as
, as  . Since
. Since  is monotone nondecreasing, one gets
is monotone nondecreasing, one gets

since  is monotone nondecreasing. Since the inequalities are nonstrict, the above subsequences might either converge to nonnegative real limits
is monotone nondecreasing. Since the inequalities are nonstrict, the above subsequences might either converge to nonnegative real limits  and
and  , or diverge to
, or diverge to  . The event that
. The event that  and
and  are one finite and the other infinity is not possible since
are one finite and the other infinity is not possible since  so that any existing discontinuity is a finite-jump type discontinuity. Thus, both limits are either finite, although eventually distinct or both are
so that any existing discontinuity is a finite-jump type discontinuity. Thus, both limits are either finite, although eventually distinct or both are  so that
so that  and
and  (and simultaneously finite or infinity) as
(and simultaneously finite or infinity) as  , where
, where  for the given
for the given  . Such a
. Such a  always exists in
always exists in  for each given
for each given  since
since  is a self-mapping on
is a self-mapping on  Then,
Then,

which is a contradiction unless  , as
, as  , as
, as  , since
, since  is continuous at
is continuous at  and
and  , if and only if
, if and only if  But, if the subsequence
But, if the subsequence  has a zero limit as
has a zero limit as  , then it is a bounded sequence. Thus,
, then it is a bounded sequence. Thus,  as
as  is false and then
is false and then  ,
,  being unbounded fails so that the contradiction follows. The right-limit convergence
being unbounded fails so that the contradiction follows. The right-limit convergence  leads to the same conclusion. As a result, there is no
leads to the same conclusion. As a result, there is no  such that
such that  ,
,  is unbounded and the result is fully proven.
is unbounded and the result is fully proven.
An alternative proof to that of Theorem 2.2(ii) related to the existence of a unique fixed point in  , follows directly by using Theorem
, follows directly by using Theorem  in [4] since
in [4] since  is a large contraction and the sequence
is a large contraction and the sequence  is uniformly bounded (Propositions 2.4 and 2.5).
is uniformly bounded (Propositions 2.4 and 2.5).
Proposition 2.6.
Let  be a complete metric space and
be a complete metric space and  be a large contraction. If
be a large contraction. If  is a modified altering-distance function which satisfies the conditions of Theorem 2.2(ii), then
is a modified altering-distance function which satisfies the conditions of Theorem 2.2(ii), then  has a unique fixed point in
has a unique fixed point in  .
.
Proof.
 is a large contraction from Proposition 2.4, since it fulfils Theorem 2.2(ii). Also,
is a large contraction from Proposition 2.4, since it fulfils Theorem 2.2(ii). Also,  , for all
, for all  and
and  from Proposition 2.5. Thus, from [4, Theorem
from Proposition 2.5. Thus, from [4, Theorem  ],
],  has a unique fixed point in
has a unique fixed point in  .
.
The following result is a direct consequence of Theorem 2.2, Propositions 2.4 and 2.5.
Proposition 2.7.
Let  be a complete metric space and
be a complete metric space and  be a weak contraction on
be a weak contraction on  . Then,
. Then,  , for all
, for all  and
and  and
and  has a unique fixed point on
has a unique fixed point on  .
.
3. 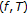 -Stability Related to a Class of Nonlinear Iterations Related to Distance and Altering-Distance Functions
-Stability Related to a Class of Nonlinear Iterations Related to Distance and Altering-Distance Functions
Assume that  is a complete metric space,
is a complete metric space,  is a self-mapping on
is a self-mapping on  . The iteration process
. The iteration process  has a fixed point if
has a fixed point if  . A necessary condition for
. A necessary condition for  to have a fixed point is that it to be injective. The
to have a fixed point is that it to be injective. The  -stability of the Picard iteration has been investigated in a set of papers (see, e.g., [5, 19, 20]). The Picard iteration is said to be
-stability of the Picard iteration has been investigated in a set of papers (see, e.g., [5, 19, 20]). The Picard iteration is said to be  -stable if
-stable if  , for all
, for all  . The subsequent result is an extension of a previous one in [5] for the so-called
. The subsequent result is an extension of a previous one in [5] for the so-called  -stability of the iteration
-stability of the iteration  , for all
, for all  if the pair
if the pair  satisfies the so-called
satisfies the so-called  property defined by
property defined by

for all  ;
;  , with
, with  and
and  , provided that the set of fixed points
, provided that the set of fixed points  is nonempty. If
is nonempty. If  is identity, then the above property is stated as
is identity, then the above property is stated as  satisfying the
satisfying the  property.
property.
Theorem 3.1.
Assume that
(1) is a complete metric space,
is a complete metric space,  is a continuous mapping, and
is a continuous mapping, and  is a self-mapping on
is a self-mapping on  such that the set of fixed points
such that the set of fixed points  of the iteration procedure
of the iteration procedure  , for all
, for all  , is nonempty;
, is nonempty;
(2)the pair  satisfies the
satisfies the  property; that is,
property; that is,  ; for all
; for all  with
with  and
and  ;
;
(3) , for all
, for all  .
.
Then, the iteration procedure  , for all
, for all  , is
, is  -stable and it possesses a unique fixed point.
-stable and it possesses a unique fixed point.
Proof.
For any given  , which exists since
, which exists since  , and for all
, and for all  such that
such that  with
with  being the computation error sequence, one has
being the computation error sequence, one has

Since  ,
,  , and
, and  , as
, as  , then,
, then,

from (3.2), [5, 6]. Also,  , as
, as  , as
, as  . Also,
. Also,

as  , since
, since  , as
, as  . From the above inequalities either
. From the above inequalities either  , as
, as  , or
, or  , with
, with  as
as  , but in this second case,
, but in this second case,  , as
, as  , is false so that
, is false so that  . Then,
. Then,  , as
, as  . Thus,
. Thus,  , as
, as  from (3.4). Then,
from (3.4). Then,  and
and  , as
, as  . Since
. Since  is injective,
is injective,  , as
, as  so that f is
so that f is  -stable. It is proven by contradiction that the fixed point of the iteration procedure
-stable. It is proven by contradiction that the fixed point of the iteration procedure  , for all
, for all  is unique. Assume that there exists
is unique. Assume that there exists  . Then,
. Then,

what is impossible if  . Then,
. Then,  .
.
Theorem 3.1 is now extended by extending the  property of the pair
property of the pair  to that of the triple
to that of the triple  , where
, where  is an appropriate continuous function.
is an appropriate continuous function.
Theorem 3.2.
Assume that
(1) is a complete metric space,
is a complete metric space,  is a continuous mapping, and
is a continuous mapping, and  is a self-mapping on
is a self-mapping on  such that the set of fixed points
such that the set of fixed points  of the iteration procedure
of the iteration procedure  , for all
, for all  , is nonempty;
, is nonempty;
(2) is continuous, satisfies
is continuous, satisfies  , possesses the subadditive property, and, furthermore, the triple
, possesses the subadditive property, and, furthermore, the triple  satisfies the
satisfies the  property defined by
property defined by  +
+  for all
for all  with
with  and
and  ;
;
(3) , for all
, for all  .
.
Then, the iteration procedure  , for all
, for all  is
is  -stable and it possesses a unique fixed point.
-stable and it possesses a unique fixed point.
Proof.
For any given  , which exists since
, which exists since  , and for all
, and for all  such that
such that  , with
, with  being the computation error sequence and, since
being the computation error sequence and, since  possesses the sub-additive property, one has
possesses the sub-additive property, one has

according to Hypothesis ( ) since
) since  and
and  from Hypothesis (
from Hypothesis ( ). Since
). Since  is everywhere continuous and satisfies
is everywhere continuous and satisfies  , then
, then  as
as  . Also,
. Also,  as
as  as
as  . The remaining of the proof follows with the same arguments as in that of Theorem 3.1.
. The remaining of the proof follows with the same arguments as in that of Theorem 3.1.
Theorem 3.3.
Assume that
(1) is a complete metric space,
is a complete metric space,  is a continuous mapping, and
is a continuous mapping, and  is a self-mapping on
is a self-mapping on  such that the set of fixed points
such that the set of fixed points  of the iteration procedure
of the iteration procedure  , for all
, for all  , is nonempty;
, is nonempty;
(2) and
and  are both continuous and monotone nondecreasing while satisfying
are both continuous and monotone nondecreasing while satisfying  , and, furthermore, the quadruple
, and, furthermore, the quadruple  satisfies the
satisfies the  property:
property:  , for all
, for all  ; and for all
; and for all  with
with  and
and  ;
;
(3) , for all
, for all  .
.
Then, the iteration procedure  , for all
, for all  is
is  -stable and it possesses a unique fixed point.
-stable and it possesses a unique fixed point.
Proof.
Since  and
and  are both continuous and monotone nondecreasing then Hypothesis (
are both continuous and monotone nondecreasing then Hypothesis ( ) implies that
) implies that  , for all
, for all  and
and  ; for all
; for all  with
with  and
and  which is Hypothesis (
which is Hypothesis ( ) of Theorem 3.1. Furthermore,
) of Theorem 3.1. Furthermore,  from the continuity of
from the continuity of  everywhere within its definition domain
everywhere within its definition domain  and its property
and its property  . Thus, the proof follows as in Theorem 3.1 since Hypothesis (
. Thus, the proof follows as in Theorem 3.1 since Hypothesis ( ) to (
) to ( ) of this theorem hold.
) of this theorem hold.
The following direct particular result of Theorems 3.1 to 3.3 follows.
Corollary 3.4.
Theorems 3.1, 3.2, and 3.3 hold "mutatis-mutandis" stated for the function  being the identity mapping on
being the identity mapping on  and
and  .
.
Corollary 3.4 referred to Theorem 3.1 was first proven in [5]. It is now of interest the removal of the condition of the set of fixed points to be nonempty by guaranteeing that is in fact nonempty consisting of a unique element under extra contractive properties of the pair  . The following result holds.
. The following result holds.
Theorem 3.5.
The following two properties hold.
(i)Consider the Picard  -iteration process
-iteration process  , for all
, for all  and
and  . If
. If  satisfies the
satisfies the  property while it is a
property while it is a  -contraction (i.e., a contractive mapping with constant
-contraction (i.e., a contractive mapping with constant  , then
, then  for some
for some  , and, furthermore,
, and, furthermore,


(ii)Consider the iteration process  , for all
, for all  and
and  . If
. If  satisfies the
satisfies the  property while the pair
property while the pair  is a
is a  -contraction (i.e., a contractive mapping with constant
-contraction (i.e., a contractive mapping with constant  , then
, then  for some
for some  , and, furthermore,
, and, furthermore,


Proof.
-
(i)
Equation (3.7) follows from the
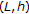 property leading to
property leading to  (3.11)
(3.11)
since  is
is  -contractive, so that it possesses a unique fixed point
-contractive, so that it possesses a unique fixed point  , and it satisfies the
, and it satisfies the  property with
property with  . Equation (3.8) follows directly from the following three inequalities:
. Equation (3.8) follows directly from the following three inequalities:

For  , for all
, for all  , one gets
, one gets

after using the  property, and
property, and

again with the use of the  property.
property.
-
(ii)
Equation (3.9) follows from the
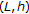 property leading to
property leading to  (3.15)
(3.15)
since the pair  is
is  -contractive and it satisfies the
-contractive and it satisfies the  property with
property with  . Equation (3.10) follows directly from the following three inequalities:
. Equation (3.10) follows directly from the following three inequalities:

since the pair (f,  ) is
) is  -contractive. Then,
-contractive. Then,

for all  and some
and some  independent of
independent of  .
.  . Therefore, for any
. Therefore, for any  , one gets
, one gets

after using the  property, and
property, and

again with the use of the  property.
property.
Theorem 3.5(ii) allows directly extending Theorem 3.1 as follows by removing the requirement of the set of fixed points to be nonempty with a unique element since this is guaranteed by the Banach contractive mapping principle.
Theorem 3.6.
Assume that:  is a complete metric space,
is a complete metric space,  is a continuous mapping on
is a continuous mapping on  , and
, and  is a self-mapping on
is a self-mapping on  such that the pair
such that the pair  is
is  -contractive and satisfies the
-contractive and satisfies the  property (provided that the set of fixed points is nonempty), that is,
property (provided that the set of fixed points is nonempty), that is,

with  being any fixed point; that is,
being any fixed point; that is,  and some real constants
and some real constants  ,
,  , and
, and  , and, furthermore,
, and, furthermore,

Then, the iteration procedure  , for all
, for all  is
is  -stable with
-stable with  being its unique fixed point, that is,
being its unique fixed point, that is,  .
.
A direct particular case of Theorem 3.5 applies directly to the case of f being the identity map on  via Theorem 3.5(i).
via Theorem 3.5(i).
Corollary 3.7.
Assume that  is a complete metric space, and
is a complete metric space, and  is a
is a  -contractive self-mapping on
-contractive self-mapping on  satisfying the
satisfying the  property, that is,
property, that is,

with  being any fixed point; that is,
being any fixed point; that is,  and some real constants
and some real constants  ,
,  , and
, and  , and, furthermore,
, and, furthermore,  , for all
, for all  . Then, the Picard iteration procedure
. Then, the Picard iteration procedure  , for all
, for all  , is
, is  -stable with
-stable with  being its unique fixed point, that is,
being its unique fixed point, that is,  .
.
Theorems 3.5 and 3.6 and Corollary 3.7 are directly extendable to the case that the pair  is a large contraction. Also, Theorem 3.6 and Corollary 3.7 can be extended directly for the use of distance functions or extended altering-distance functions as follows.
is a large contraction. Also, Theorem 3.6 and Corollary 3.7 can be extended directly for the use of distance functions or extended altering-distance functions as follows.
Theorem 3.8.
Assume that
(1) is a complete metric space,
is a complete metric space,  is a continuous mapping on
is a continuous mapping on  , and
, and  is a self-mapping on
is a self-mapping on  ;
;
(2) is an extended altering-distance function (Definition 2.1) satisfying the conditions of Theorem 2.2(ii) with some monotone nondecreasing function
is an extended altering-distance function (Definition 2.1) satisfying the conditions of Theorem 2.2(ii) with some monotone nondecreasing function  satisfying
satisfying  , for all
, for all  , and
, and  , if and only if
, if and only if  ;
;
(3)the quadruple  satisfies the following
satisfies the following  property:
property:

for all  , and
, and  with real constants
with real constants  and
and  ;
;
(4) , for all
, for all  .
.
Then, the iteration procedure  , for all
, for all  , is
, is  -stable with
-stable with  being its unique fixed point, that is,
being its unique fixed point, that is,  .
.
Corollary 3.9.
Assume that Assumptions ( ) and (
) and ( ) of Theorem 3.8 hold, and, furthermore,
) of Theorem 3.8 hold, and, furthermore,
(1) is an altering-distance function satisfying the conditions of Theorem 2.2(i), for all
is an altering-distance function satisfying the conditions of Theorem 2.2(i), for all  , satisfying
, satisfying  , if and only if
, if and only if  ;
;
(2)the triple  satisfies the following
satisfies the following  property:
property:

for all  , and
, and  with real constants
with real constants  and
and  ;
;
(3) , for all
, for all  .
.
Then, the iteration procedure  , for all
, for all  is
is  -stable with
-stable with  being its unique fixed point, that is,
being its unique fixed point, that is,  .
.
References
Khan MS, Swaleh M, Sessa S: Fixed point theorems by altering distances between the points. Bulletin of the Australian Mathematical Society 1984,30(1):1–9. 10.1017/S0004972700001659
Dutta PN, Choudhury BS: A generalisation of contraction principle in metric spaces. Fixed Point Theory and Applications 2008, 2008:-8.
Chidume CE, Zegeye H, Aneke SJ: Approximation of fixed points of weakly contractive nonself maps in Banach spaces. Journal of Mathematical Analysis and Applications 2002,270(1):189–199. 10.1016/S0022-247X(02)00063-X
Burton TA: Stability by Fixed Point Theory for Functional Differential Equations. Dover, Mineola, NY, USA; 2006:xiv+348.
Qing Y, Rhoades BE: T -stability of Picard iteration in metric spaces. Fixed Point Theory and Applications 2008, 2008:-4.
Liu Q: A convergence theorem of the sequence of Ishikawa iterates for quasi-contractive mappings. Journal of Mathematical Analysis and Applications 1990,146(2):301–305. 10.1016/0022-247X(90)90303-W
Chen C, Zhu C: Fixed point theorems for n times reasonable expansive mapping. Fixed Point Theory and Applications 2008, 2008:-6.
Mendel JM: Discrete Techniques of Parameter Estimation: The Equation Error Formulation. Marcel Dekker, New York, NY, USA; 1973:xiv+385.
De la Sen M: About robust stability of dynamic systems with time delays through fixed point theory. Fixed Point Theory and Applications 2008, -20.
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Hu LG: Strong convergence of a modified Halpern's iteration for nonexpansive mappings. Fixed Point Theory and Applications 2008, -9.
Saeidi S: Approximating common fixed points of Lipschitzian semigroup in smooth Banach spaces. Fixed Point Theory and Applications 2008, -17.
Lions PL: Approximation de points fixes de contractions. Comptes Rendus de l'Académie des sciences 1977,284(21):A1357-A1359.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Aleyner A, Reich S: An explicit construction of sunny nonexpansive retractions in Banach spaces. Fixed Point Theory and Applications 2005,2005(3):295–305.
Xu HK: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Benavides TD, Acedo GL, Xu HK: Construction of sunny nonexpansive retractions in Banach spaces. Bulletin of the Australian Mathematical Society 2002,66(1):9–16. 10.1017/S0004972700020621
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Popescu O: T- stability of Picard iteration in metric spaces. Bulletin of the Transilvania University of Brasov, Series III 2009,2(51):211–214.
Thorlund L: Fixed point iterations and global stability in economics. Mathematics of Operations Research 1985,10(4):642–649. 10.1287/moor.10.4.642
Agarwal RP, O'Regan Donal, Sahu DR: Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. Journal of Nonlinear and Convex Analysis 2007,8(1):61–79.
De la Sen M: Some combined relations between contractive mappings, Kannan mappings, reasonable expansive mappings, and T -stability. Fixed Point Theory and Applications 2009, 2009:-25.
Agarwal RP: Boundary value problems for second order differential equations of Sobolev type. Computers & Mathematics with Applications 1988,15(2):107–118. 10.1016/0898-1221(88)90080-6
Lau ATM, Miyake H, Takahashi W: Approximation of fixed points for amenable semigroups of nonexpansive mappings in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2007,67(4):1211–1225. 10.1016/j.na.2006.07.008
Acknowledgments
The author is very grateful to the Spanish Ministry of Education for its partial support of this work through Grant DPI2009-07197. He is also grateful to the Basque Government for its support through Grants IT378-10, SAIOTEK S-PE08UN15, and SAIOTEK SPE07UN04.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M. Stable Iteration Procedures in Metric Spaces which Generalize a Picard-Type Iteration. Fixed Point Theory Appl 2010, 953091 (2010). https://doi.org/10.1155/2010/953091
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/953091
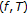 -Stability Related to a Class of Nonlinear Iterations Related to Distance and Altering-Distance Functions
-Stability Related to a Class of Nonlinear Iterations Related to Distance and Altering-Distance Functions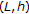 property leading to
property leading to 
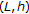 property leading to
property leading to 