- Research Article
- Open access
- Published:
Best Proximity Points of Cyclic 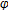 -Contractions on Reflexive Banach Spaces
-Contractions on Reflexive Banach Spaces
Fixed Point Theory and Applications volume 2010, Article number: 946178 (2010)
Abstract
We provide a positive answer to a question raised by Al-Thagafi and Shahzad (Nonlinear Analysis, 70 (2009), 3665-3671) about best proximity points of cyclic  -contractions on reflexive Banach spaces.
-contractions on reflexive Banach spaces.
1. Introduction
As a generalization of Banach contraction principle, Kirk et al. proved, in 2003, the following fixed point result; see [1].
Theorem 1.1.
Let  and
and  be nonempty closed subsets of a complete metric space
be nonempty closed subsets of a complete metric space  . Suppose that
. Suppose that  is a map satisfying
is a map satisfying  ,
,  and there exists
and there exists  such that
such that  for all
for all  and
and  . Then,
. Then,  has a unique fixed point in
has a unique fixed point in  .
.
Let  and
and  be nonempty closed subsets of a metric space
be nonempty closed subsets of a metric space  and
and a strictly increasing map. We say that
a strictly increasing map. We say that  is a cyclic
is a cyclic  -contraction map [2] whenever
-contraction map [2] whenever  ,
,  and
and

for all  and
and  , where
, where  . Also,
. Also,  is called a best proximity point if
is called a best proximity point if  . As a special case, when
. As a special case, when  , in which
, in which  is a constant,
is a constant,  is called cyclic contraction.
is called cyclic contraction.
In 2005, Petru el proved some periodic point results for cyclic contraction maps [3]. Then, Eldered and Veeramani proved some results on best proximity points of cyclic contraction maps in 2006 [4]. They raised a question about the existence of a best proximity point for a cyclic contraction map in a reflexive Banach space. In 2009, Al-Thagafi and Shahzad gave a positive answer to the question [2]. More precisely, they proved some results on the existence and convergence of best proximity points of cyclic contraction maps defined on reflexive (and strictly convex) Banach spaces [2, Theorems 9, 10, 11, and 12]. They also introduced cyclic
el proved some periodic point results for cyclic contraction maps [3]. Then, Eldered and Veeramani proved some results on best proximity points of cyclic contraction maps in 2006 [4]. They raised a question about the existence of a best proximity point for a cyclic contraction map in a reflexive Banach space. In 2009, Al-Thagafi and Shahzad gave a positive answer to the question [2]. More precisely, they proved some results on the existence and convergence of best proximity points of cyclic contraction maps defined on reflexive (and strictly convex) Banach spaces [2, Theorems 9, 10, 11, and 12]. They also introduced cyclic  -contraction maps and raised the following question in [2].
-contraction maps and raised the following question in [2].
Question 1.
It is interesting to ask whether Theorems 9 and 10 (resp., Theorems 11 and 12) hold for cyclic  -contraction maps where the space is only reflexive (resp., reflexive and strictly convex) Banach space.
-contraction maps where the space is only reflexive (resp., reflexive and strictly convex) Banach space.
In this paper, we provide a positive answer to the above question. For obtaining the answer, we use some results of [2].
2. Main Results
First, we give the following extension of [4, Proposition 3.3] for cyclic  -contraction maps, where
-contraction maps, where  is unbounded.
is unbounded.
Theorem 2.1.
Let  be a strictly increasing unbounded map. Also, let
be a strictly increasing unbounded map. Also, let  and
and  be nonempty subsets of a metric space
be nonempty subsets of a metric space  ,
,  a cyclic
a cyclic  -contraction map,
-contraction map,  and
and  for all
for all  . Then, the sequences
. Then, the sequences  and
and  are bounded.
are bounded.
Proof.
Suppose that  (the proof when
(the proof when  is similar). By [2, Theorem 3],
is similar). By [2, Theorem 3],  . Hence, it is sufficient to prove that
. Hence, it is sufficient to prove that  is bounded. Since
is bounded. Since  is unbounded, there exists
is unbounded, there exists  such that
such that

If  is not bounded, then there exists a natural number
is not bounded, then there exists a natural number  such that
such that

Then, we have

Since  for all
for all  and
and  , we obtain
, we obtain

Since  , we have
, we have

Thus, we obtain  . Since
. Since

 . Hence,
. Hence,  . This contradiction completes the proof.
. This contradiction completes the proof.
Since the proof of last result was classic, we presented it separately. Here, we provide our key result via a special proof which is a general case of Theorem 2.1.
Theorem 2.2.
Let  be a strictly increasing map. Also, let
be a strictly increasing map. Also, let  and
and  be nonempty subsets of a metric space
be nonempty subsets of a metric space  ,
,  a cyclic
a cyclic  -contraction map,
-contraction map,  , and
, and  for all
for all  . Then, the sequences
. Then, the sequences  and
and  are bounded.
are bounded.
Proof.
Suppose that  (the proof when
(the proof when  is similar). By [2, Theorem 3],
is similar). By [2, Theorem 3],  . Hence, either
. Hence, either  and
and  are bounded or both are unbounded. Suppose that both sequences are unbounded. Fix
are bounded or both are unbounded. Suppose that both sequences are unbounded. Fix  and define
and define

for all  . Since
. Since  is unbounded,
is unbounded,  for all
for all  . Thus, we can choose a strictly increasing subsequence
. Thus, we can choose a strictly increasing subsequence  of the sequence
of the sequence  . Since
. Since  , we have
, we have

Again, we can choose a strictly increasing subsequence  of the sequence
of the sequence  such that
such that  . By continuing this process, for each natural number
. By continuing this process, for each natural number  , we can choose a strictly increasing subsequence
, we can choose a strictly increasing subsequence  of the sequence
of the sequence  such that
such that  . By the construction, if we consider the sequence
. By the construction, if we consider the sequence  , then
, then  ,
,  is a strictly increasing subsequence of
is a strictly increasing subsequence of  and
and  for all
for all  . Now, define
. Now, define  . Also, by induction define the sequence
. Also, by induction define the sequence  by
by  . Note that, the sequence
. Note that, the sequence  is strictly increasing and
is strictly increasing and  . Since
. Since  is a cyclic
is a cyclic  -contraction map,
-contraction map,  is a decreasing sequence. Hence by the construction of the sequence
is a decreasing sequence. Hence by the construction of the sequence  ,
,  is a decreasing sequence. Let
is a decreasing sequence. Let  be given. Since
be given. Since  , we have
, we have

Thus,

for all  . Hence, we have
. Hence, we have

for all  . Since
. Since  for all
for all  and
and  , we obtain
, we obtain

for all  . Consequently
. Consequently

for all  . This implies that
. This implies that

for all  , where
, where

is a constant. But,  for all
for all  . This contradiction completes the proof.
. This contradiction completes the proof.
Now by using this key result, we provide our main results which give positive answer to the question. Their proofs are basically due to Al-Thagafi and Shahzad [2]. However, the crucial role is played by our key result. Weak convergence of  to
to  is denoted by
is denoted by  .
.
Theorem 2.3.
Let  be a strictly increasing map. Also, let
be a strictly increasing map. Also, let  and
and  be nonempty weakly closed subsets of a reflexive Banach space and
be nonempty weakly closed subsets of a reflexive Banach space and  a cyclic
a cyclic  -contraction map. Then there exists
-contraction map. Then there exists  such that
such that

Proof.
If  , the result follows from [2, Theorem 1]. So, we assume that
, the result follows from [2, Theorem 1]. So, we assume that  . For
. For  , define
, define  for all
for all  . By Theorem 2.2, the sequences
. By Theorem 2.2, the sequences  and
and  are bounded. Since
are bounded. Since  is reflexive and
is reflexive and  is weakly closed, the sequence
is weakly closed, the sequence  has a subsequence
has a subsequence  such that
such that  . As
. As  is bounded and
is bounded and  is weakly closed, we can say, without loss of generality, that
is weakly closed, we can say, without loss of generality, that  as
as  . Since
. Since  as
as  , there exists a bounded linear functional
, there exists a bounded linear functional  such that
such that  and
and  . For each
. For each  , we have
, we have

Since  , by using [2, Theorem 3] we obtain
, by using [2, Theorem 3] we obtain

Hence,  .
.
Definition 2.4.
(see [2]) Let  and
and  be nonempty subsets of a normed space
be nonempty subsets of a normed space  ,
,  ,
,  , and
, and  . We say that
. We say that  satisfies the proximal property if
satisfies the proximal property if

Theorem 2.5.
Let  be a strictly increasing map. Also, let
be a strictly increasing map. Also, let  and
and  be nonempty subsets of a reflexive Banach space
be nonempty subsets of a reflexive Banach space  such that
such that  is weakly closed and
is weakly closed and  a cyclic
a cyclic  -contraction map. Then, there exists
-contraction map. Then, there exists  such that
such that  provided that one of the following conditions is satisfied
provided that one of the following conditions is satisfied
(a) is weakly continuous on
is weakly continuous on  .
.
(b) satisfies the proximal property.
satisfies the proximal property.
Proof.
If  , the result follows from [2, Theorem 1]. So, we assume that
, the result follows from [2, Theorem 1]. So, we assume that  . For
. For  , define
, define  for all
for all  . By Theorem 2.2, the sequence
. By Theorem 2.2, the sequence  is bounded. Since
is bounded. Since  is reflexive and
is reflexive and  is weakly closed, the sequence
is weakly closed, the sequence  has a subsequence
has a subsequence  such that
such that  as
as  .
.
(a)Since  is weakly continuous on
is weakly continuous on  and
and  , we have
, we have  as
as  . So
. So  as
as  . The rest of the proof is similar to that of Theorem 2.3.
. The rest of the proof is similar to that of Theorem 2.3.
(b)By [2, Theorem 3], we have

as  . Since
. Since  satisfies the proximal property, we have
satisfies the proximal property, we have  .
.
Theorem 2.6.
Let  be a strictly increasing map. Also, let
be a strictly increasing map. Also, let  and
and  be nonempty closed and convex subsets of a reflexive and strictly convex Banach space and
be nonempty closed and convex subsets of a reflexive and strictly convex Banach space and  a cyclic
a cyclic  -contraction map. If
-contraction map. If  , then there exists a unique
, then there exists a unique  such that
such that  and
and  .
.
Proof.
If  , the result follows from [2, Theorem 1]. So, we assume that
, the result follows from [2, Theorem 1]. So, we assume that  . Since
. Since  is closed and convex, it is weakly closed. By Theorem 2.3, there exists
is closed and convex, it is weakly closed. By Theorem 2.3, there exists  with
with  . To show the uniqueness of
. To show the uniqueness of  , suppose that there exists another
, suppose that there exists another  with
with  . Since
. Since  , we conclude that
, we conclude that  . As both
. As both  and
and  are convex, by the strict convexity of
are convex, by the strict convexity of  , we have
, we have

which is a contradiction. Since  , we obtain, from the uniqueness of
, we obtain, from the uniqueness of  , that
, that  . Hence
. Hence  ,
,  and
and  .
.
Theorem 2.7.
Let  be a strictly increasing map. Also, let
be a strictly increasing map. Also, let  and
and  be nonempty subsets of a reflexive and strictly convex Banach space
be nonempty subsets of a reflexive and strictly convex Banach space  such that
such that  is closed and convex and
is closed and convex and  a cyclic
a cyclic  -contraction map. Then, there exists a unique
-contraction map. Then, there exists a unique  such that
such that  and
and  provided that one of the following conditions is satisfied
provided that one of the following conditions is satisfied
(a) is weakly continuous on
is weakly continuous on  .
.
(b) satisfies the proximal property.
satisfies the proximal property.
Proof.
If  , the result follows from [2, Theorem 1]. So, we assume that
, the result follows from [2, Theorem 1]. So, we assume that  . Since
. Since  is closed and convex, it is weakly closed. By Theorem 2.5 that there exists
is closed and convex, it is weakly closed. By Theorem 2.5 that there exists  with
with  . Thus,
. Thus,  . Indeed, if we assume that
. Indeed, if we assume that  . Then from the convexity of
. Then from the convexity of  and the strict convexity of
and the strict convexity of  , we have
, we have

which is a contradiction. The uniqueness of  follows as in the proof of [2, Theorem 8].
follows as in the proof of [2, Theorem 8].
References
Kirk WA, Srinivasan PS, Veeramani P: Fixed points for mappings satisfying cyclical contractive conditions. Fixed Point Theory 2003,4(1):79–89.
Al-Thagafi MA, Shahzad N: Convergence and existence results for best proximity points. Nonlinear Analysis. Theory, Methods & Applications 2009,70(10):3665–3671. 10.1016/j.na.2008.07.022
Petruşel G: Cyclic representations and periodic points. Universitatis Babeş-Bolyai. Studia. Mathematica 2005,50(3):107–112.
Eldred AA, Veeramani P: Existence and convergence of best proximity points. Journal of Mathematical Analysis and Applications 2006,323(2):1001–1006. 10.1016/j.jmaa.2005.10.081
Acknowledgment
The authors express their gratitude to the referees for their helpful suggestions concerning the final version of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rezapour, S., Derafshpour, M. & Shahzad, N. Best Proximity Points of Cyclic 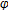 -Contractions on Reflexive Banach Spaces.
Fixed Point Theory Appl 2010, 946178 (2010). https://doi.org/10.1155/2010/946178
-Contractions on Reflexive Banach Spaces.
Fixed Point Theory Appl 2010, 946178 (2010). https://doi.org/10.1155/2010/946178
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/946178