- Research Article
- Open access
- Published:
A Set of Axioms for the Degree of a Tangent Vector Field on Differentiable Manifolds
Fixed Point Theory and Applications volume 2010, Article number: 845631 (2010)
Abstract
Given a tangent vector field on a finite-dimensional real smooth manifold, its degree (also known as characteristic or rotation) is, in some sense, an algebraic count of its zeros and gives useful information for its associated ordinary differential equation. When, in particular, the ambient manifold is an open subset  of
of  , a tangent vector field
, a tangent vector field  on
on  can be identified with a map
can be identified with a map  , and its degree, when defined, coincides with the Brouwer degree with respect to zero of the corresponding map
, and its degree, when defined, coincides with the Brouwer degree with respect to zero of the corresponding map  . As is well known, the Brouwer degree in
. As is well known, the Brouwer degree in  is uniquely determined by three axioms called Normalization, Additivity, and Homotopy Invariance. Here we shall provide a simple proof that in the context of differentiable manifolds the degree of a tangent vector field is uniquely determined by suitably adapted versions of the above three axioms.
is uniquely determined by three axioms called Normalization, Additivity, and Homotopy Invariance. Here we shall provide a simple proof that in the context of differentiable manifolds the degree of a tangent vector field is uniquely determined by suitably adapted versions of the above three axioms.
1. Introduction
The degree of a tangent vector field on a differentiable manifold is a very well-known tool of nonlinear analysis used, in particular, in the theory of ordinary differential equations and dynamical systems. This notion is more often known by the names of rotation or of (Euler) characteristic of a vector field (see, e.g., [1–6]). Here, we depart from the established tradition by choosing the name "degree" because of the following consideration: in the case that the ambient manifold is an open subset  of
of  , there is a natural identification of a vector field
, there is a natural identification of a vector field  on
on  with a map
with a map  , and the degree
, and the degree  of
of  on
on  , when defined, is just the Brouwer degree
, when defined, is just the Brouwer degree  of
of  on
on  with respect to zero. Thus the degree of a vector field can be seen as a generalization to the context of differentiable manifolds of the notion of Brouwer degree in
with respect to zero. Thus the degree of a vector field can be seen as a generalization to the context of differentiable manifolds of the notion of Brouwer degree in  . As is well-known, this extension of
. As is well-known, this extension of  does not require the orientability of the underlying manifold, and is therefore different from the classical extension of
does not require the orientability of the underlying manifold, and is therefore different from the classical extension of  for maps acting between oriented differentiable manifolds.
for maps acting between oriented differentiable manifolds.
A result of Amann and Weiss [7] (see also [8]) asserts that the Brouwer degree in  is uniquely determined by three axioms: Normalization, Additivity, and Homotopy Invariance. A similar statement is true (e.g., as a consequence of a result of Staecker [9]) for the degree of maps between oriented differentiable manifolds of the same dimension. In this paper, which is closely related in both spirit and demonstrative techniques to [10], we will prove that suitably adapted versions of the above axioms are sufficient to uniquely determine the degree of a tangent vector field on a (not necessarily orientable) differentiable manifold. We will not deal with the problem of existence of such a degree, for which we refer to [1–5].
is uniquely determined by three axioms: Normalization, Additivity, and Homotopy Invariance. A similar statement is true (e.g., as a consequence of a result of Staecker [9]) for the degree of maps between oriented differentiable manifolds of the same dimension. In this paper, which is closely related in both spirit and demonstrative techniques to [10], we will prove that suitably adapted versions of the above axioms are sufficient to uniquely determine the degree of a tangent vector field on a (not necessarily orientable) differentiable manifold. We will not deal with the problem of existence of such a degree, for which we refer to [1–5].
2. Preliminaries
Given two sets  and
and  , by a local map with source
, by a local map with source and target
and target we mean a triple
we mean a triple  , where
, where  , the graph of
, the graph of  , is a subset of
, is a subset of  such that for any
such that for any  there exists at most one
there exists at most one  with
with  . The domain
. The domain  of
of  is the set of all
is the set of all  for which there exists
for which there exists  such that
such that  ; that is,
; that is,  , where
, where  denotes the projection of
denotes the projection of  onto the first factor. The restriction of a local map
onto the first factor. The restriction of a local map  to a subset
to a subset  of
of  is the triple
is the triple

with domain  .
.
Incidentally, we point out that sets and local maps (with the obvious composition) constitute a category. Although the notation  would be acceptable in the context of category theory, it will be reserved for the case when
would be acceptable in the context of category theory, it will be reserved for the case when  .
.
Whenever it makes sense (e.g., when source and target spaces are differentiable manifolds), local maps are tacitly assumed to be continuous.
Throughout the paper all of the differentiable manifolds will be assumed to be finite dimensional, smooth, real, Hausdorff, and second countable. Thus, they can be embedded in some  . Moreover,
. Moreover,  and
and  will always denote arbitrary differentiable manifolds. Given any
will always denote arbitrary differentiable manifolds. Given any  ,
,  will denote the tangent space of
will denote the tangent space of  at
at  . Furthermore
. Furthermore  will be the tangent bundle of
will be the tangent bundle of  ; that is,
; that is,

The map  given by
given by  will be the bundle projection of
will be the bundle projection of  . It will also be convenient, given any
. It will also be convenient, given any  , to denote by
, to denote by  the zero element of
the zero element of  .
.
Given a smooth map  , by
, by  we will mean the map that to each
we will mean the map that to each  associates
associates  . Here
. Here  denotes the differential of
denotes the differential of  at
at  . Notice that if
. Notice that if  is a diffeomorphism, then so is
is a diffeomorphism, then so is  and one has
and one has  .
.
By a local tangent vector field on we mean a local map
we mean a local map  having
having  as source and
as source and  as target, with the property that the composition
as target, with the property that the composition  is the identity on
is the identity on  . Therefore, given a local tangent vector field
. Therefore, given a local tangent vector field  on
on  , for all
, for all  there exists
there exists  such that
such that  .
.
Let  and
and  be differentiable manifolds and let
be differentiable manifolds and let  be a diffeomorphism. Recall that two tangent vector fields
be a diffeomorphism. Recall that two tangent vector fields  and
and  correspond under
correspond under if the following diagram commutes:
if the following diagram commutes:

Let  be an open subset of
be an open subset of  and suppose that
and suppose that  is a local tangent vector field on
is a local tangent vector field on  with
with  . We say that
. We say that  is identity-like on
is identity-like on  if there exists a diffeomorphism
if there exists a diffeomorphism  of
of  onto
onto  such that
such that  and the identity in
and the identity in  correspond under
correspond under  . Notice that any diffeomorphism
. Notice that any diffeomorphism  from an open subset
from an open subset  of
of  onto
onto  induces an identity-like vector field on
induces an identity-like vector field on  .
.
Let  be a local tangent vector field on
be a local tangent vector field on  and let
and let  be a zero of
be a zero of  ; that is,
; that is,  . Consider a diffeomorphism
. Consider a diffeomorphism  of a neighborhood
of a neighborhood  of
of  onto
onto  and let
and let  be the tangent vector field on
be the tangent vector field on  that corresponds to
that corresponds to  under
under  . Since
. Since  , then the map
, then the map  associated to
associated to  sends
sends  into itself. Assuming that
into itself. Assuming that  is smooth in a neighborhood of
is smooth in a neighborhood of  , the function
, the function  is Fréchet differentiable at
is Fréchet differentiable at  . Denote by
. Denote by  its Fréchet derivative and let
its Fréchet derivative and let  be the endomorphism of
be the endomorphism of  which makes the following diagram commutative:
which makes the following diagram commutative:

Using the fact that  is a zero of
is a zero of  , it is not difficult to prove that
, it is not difficult to prove that  does not depend on the choice of
does not depend on the choice of  . This endomorphism of
. This endomorphism of  is called the linearization of
is called the linearization of  at
at  . Observe that, when
. Observe that, when  , the linearization
, the linearization  of a tangent vector field
of a tangent vector field  at a zero
at a zero  is just the Fréchet derivative
is just the Fréchet derivative  at
at  of the map
of the map  associated to
associated to  .
.
The following fact will play an important rôle in the proof of our main result.
Remark 2.1.
Let  ,
,  ,
,  , and
, and  be as above. Then, the commutativity of diagram (2.3) implies
be as above. Then, the commutativity of diagram (2.3) implies

3. Degree of a Tangent Vector Field
Given an open subset  of
of  and a local tangent vector field
and a local tangent vector field  on
on  , the pair
, the pair  is said to be admissible on
is said to be admissible on if
if  and the set
and the set

of the zeros of  in
in  is compact. In particular,
is compact. In particular,  is admissible if the closure
is admissible if the closure  of
of  is a compact subset of
is a compact subset of  and
and  is nonzero on the boundary
is nonzero on the boundary  of
of  .
.
Given an open subset  of
of  and a (continuous) local map
and a (continuous) local map  with source
with source  and target
and target  , we say that
, we say that  is a homotopy of tangent vector fields on
is a homotopy of tangent vector fields on if
if  , and if
, and if  is a local tangent vector field for all
is a local tangent vector field for all  . If, in addition, the set
. If, in addition, the set

is compact, the homotopy  is said to be admissible. Thus, if
is said to be admissible. Thus, if  is compact and
is compact and  , a sufficient condition for
, a sufficient condition for  to be admissible on
to be admissible on  is the following:
is the following:

which, by abuse of terminology, will be referred to as " is nonzero on
is nonzero on  ".
".
We will show that there exists at most one function that, to any admissible pair  , assigns a real number
, assigns a real number  called the degree (or characteristic or rotation) of the tangent vector field
called the degree (or characteristic or rotation) of the tangent vector field on
on , which satisfies the following three properties that will be regarded as axioms. Moreover, this function (if it exists) must be integer valued.
, which satisfies the following three properties that will be regarded as axioms. Moreover, this function (if it exists) must be integer valued.
Normalization
Let  be identity-like on an open subset
be identity-like on an open subset  of
of  . Then,
. Then,

Additivity
Given an admissible pair  , if
, if  and
and  are two disjoint open subsets of
are two disjoint open subsets of  such that
such that  , then
, then

Homotopy Invariance
If  is an admissible homotopy on
is an admissible homotopy on  , then
, then

From now on we will assume the existence of a function  defined on the family of all admissible pairs and satisfying the above three properties that we will regard as axioms.
defined on the family of all admissible pairs and satisfying the above three properties that we will regard as axioms.
Remark 3.1.
The pair  is admissible. This includes the case when
is admissible. This includes the case when  is the empty set (
is the empty set ( is coherent with the notion of local tangent vector field). A simple application of the Additivity Property shows that
is coherent with the notion of local tangent vector field). A simple application of the Additivity Property shows that  and
and  .
.
As a consequence of the Additivity Property and Remark 3.1, one easily gets the following (often neglected) property, which shows that the degree of an admissible pair  does not depend on the behavior of
does not depend on the behavior of  outside
outside  . To prove it, take
. To prove it, take  and
and  in the Additivity Property.
in the Additivity Property.
Localization
If  is admissible, then
is admissible, then 
A further important property of the degree of a tangent vector field is the following.
Excision
Given an admissible pair  and an open subset
and an open subset  of
of  containing
containing  , one has
, one has  .
.
To prove this property, observe that by Additivity, Remark 3.1, and Localization one gets

As a consequence, we have the following property.
Solution
If  , then
, then  .
.
To obtain it, observe that if  , taking
, taking  , we get
, we get

4. The Degree for Linear Vector Fields
By  we will mean the normed space of linear endomorphisms of
we will mean the normed space of linear endomorphisms of  , and by
, and by  we will denote the group of invertible ones. In this section we will consider linear vector fields on
we will denote the group of invertible ones. In this section we will consider linear vector fields on  , namely, vector fields
, namely, vector fields  with the property that
with the property that  . Notice that
. Notice that  , with
, with  a linear vector field, is an admissible pair if and only if
a linear vector field, is an admissible pair if and only if  .
.
The following consequence of the axioms asserts that the degree of an admissible pair  , with
, with  , is either
, is either  or
or  .
.
Lemma 4.1.
Let  be a nonsingular linear operator in
be a nonsingular linear operator in  . Then
. Then

Proof.
It is well-known (see, e.g., [11]) that  has exactly two connected components. Equivalently, the following two subsets of
has exactly two connected components. Equivalently, the following two subsets of  are connected:
are connected:

Since the connected sets  and
and  are open in
are open in  , they are actually path connected. Consequently, given a linear tangent vector field
, they are actually path connected. Consequently, given a linear tangent vector field  on
on  with
with  , Homotopy Invariance implies that
, Homotopy Invariance implies that  depends only on the component of
depends only on the component of  containing
containing  . Therefore, if
. Therefore, if  , one has
, one has  , where
, where  is the identity on
is the identity on  . Thus, by Normalization, we get
. Thus, by Normalization, we get

It remains to prove that  when
when  . For this purpose consider the vector field
. For this purpose consider the vector field  determined by
determined by

Notice that  is well defined because
is well defined because  is compact. Observe also that
is compact. Observe also that  is zero, because
is zero, because  is admissibly homotopic in
is admissibly homotopic in  to the never-vanishing vector field
to the never-vanishing vector field  given by
given by  .
.
Let  and
and  denote, respectively, the open half-spaces of the points in
denote, respectively, the open half-spaces of the points in  with negative and positive last coordinate. Consider the two solutions
with negative and positive last coordinate. Consider the two solutions

of the equation  and observe that
and observe that  ,
,  .
.
By Additivity (and taking into account the Localization property), we get

Now, observe that  in
in  coincides with the vector field
coincides with the vector field  determined by
determined by

which is admissibly homotopic (in  ) to the tangent vector field
) to the tangent vector field  , given by
, given by  . Therefore, because of the properties of Localization, Excision, Homotopy Invariance, and Normalization, one has
. Therefore, because of the properties of Localization, Excision, Homotopy Invariance, and Normalization, one has

which, by (4.6), implies that

Notice that  in
in  coincides with the vector field
coincides with the vector field  defined by
defined by

which is admissibly homotopic (in  ) to the linear vector field
) to the linear vector field  defined by
defined by  with
with

Thus, by Homotopy Invariance, Excision, Localization, and formula (4.9)

Hence,  being path connected, we finally get
being path connected, we finally get  for all linear tangent vector fields
for all linear tangent vector fields  on
on  such that
such that  , and the proof is complete.
, and the proof is complete.
We conclude this section with a consequence as well as an extension of Lemma 4.1. The Euclidean norm of an element  will be denoted by
will be denoted by  .
.
Lemma 4.2.
Let  be a local vector field on
be a local vector field on  and let
and let  be open and such that the equation
be open and such that the equation  has a unique solution
has a unique solution  . If
. If  is smooth in a neighborhood of
is smooth in a neighborhood of  and the linearization
and the linearization  of
of  at
at  is invertible, then
is invertible, then  .
.
Proof.
Since  is Fréchet differentiable at
is Fréchet differentiable at  and
and  , we have
, we have

where  is a continuous function such that
is a continuous function such that  . Consider the vector field
. Consider the vector field  determined by
determined by  , and let
, and let  be the homotopy on
be the homotopy on  , joining
, joining  with
with  , defined by
, defined by

For all  in
in  we have
we have

where  is positive because
is positive because  is invertible. This shows that there exists a neighborhood
is invertible. This shows that there exists a neighborhood  of
of  such that
such that  coincides with the compact set
coincides with the compact set  . Thus, by Excision and Homotopy Invariance,
. Thus, by Excision and Homotopy Invariance,

Let  be the linear tangent vector field given by
be the linear tangent vector field given by  . Clearly,
. Clearly,  is admissibly homotopic to
is admissibly homotopic to  in
in  . By Excision, Homotopy Invariance, and Lemma 4.1, we get
. By Excision, Homotopy Invariance, and Lemma 4.1, we get

The assertion now follows from (4.16), (4.17), and the fact that  coincides with
coincides with  .
.
5. The Uniqueness Result
Given a local tangent vector field  on
on  , a zero
, a zero  of
of  is called nondegenerate if
is called nondegenerate if  is smooth in a neighborhood of
is smooth in a neighborhood of  and its linearization
and its linearization  at
at  is an automorphism of
is an automorphism of  . It is known that this is equivalent to the assumption that
. It is known that this is equivalent to the assumption that  is transversal at
is transversal at  to the zero section
to the zero section  of
of  (for the theory of transversality see, e.g., [3, 4]). We recall that a nondegenerate zero is, in particular, an isolated zero.
(for the theory of transversality see, e.g., [3, 4]). We recall that a nondegenerate zero is, in particular, an isolated zero.
Let  be a local tangent vector field on
be a local tangent vector field on  . A pair
. A pair  will be called nondegenerate if
will be called nondegenerate if  is a relatively compact open subset of
is a relatively compact open subset of  ,
,  is smooth on a neighborhood of the closure
is smooth on a neighborhood of the closure  of
of  , being nonzero on
, being nonzero on  , and all its zeros in
, and all its zeros in  are nondegenerate. Note that, in this case,
are nondegenerate. Note that, in this case,  is an admissible pair and
is an admissible pair and  is a discrete set and therefore finite because it is closed in the compact set
is a discrete set and therefore finite because it is closed in the compact set  .
.
The following result, which is an easy consequence of transversality theory, shows that the computation of the degree of any admissible pair can be reduced to that of a nondegenerate pair.
Lemma 5.1.
Let  be a local tangent vector field on
be a local tangent vector field on  and let
and let  be admissible. Let
be admissible. Let  be a relatively compact open subset of
be a relatively compact open subset of  containing
containing  and such that
and such that  . Then, there exists a local tangent vector field
. Then, there exists a local tangent vector field  on
on  which is admissibly homotopic to
which is admissibly homotopic to  in
in  and such that
and such that  is a nondegenerate pair. Consequently,
is a nondegenerate pair. Consequently,  .
.
Proof.
Without loss of generality we can assume that  . Let
. Let

From the Transversality theorem (see, e.g., [3, 4]) it follows that one can find a smooth tangent vector field  that is transversal to the zero section
that is transversal to the zero section  of
of  and such that
and such that

Since  is closed in
is closed in  , the set
, the set  is a compact subset of
is a compact subset of  . Thus, this inequality shows that
. Thus, this inequality shows that  is admissible. Moreover, at any zero
is admissible. Moreover, at any zero  the endomorphism
the endomorphism  is invertible. This implies that
is invertible. This implies that  is nondegenerate.
is nondegenerate.
The conclusion follows by observing that the homotopy  on
on  of tangent vector fields given by
of tangent vector fields given by

is nonzero on  and therefore it is admissible on
and therefore it is admissible on  . The last assertion follows from Excision, and Homotopy Invariance.
. The last assertion follows from Excision, and Homotopy Invariance.
Theorem 5.2 below provides a formula for the computation of the degree of a tangent vector field that is valid for any nondegenerate pair. This implies the existence of at most one real function on the family of admissible pairs that satisfies the axioms for the degree of a tangent vector field. We recall that the property of Localization as well as Lemmas 5.1 and 4.2, which are needed in the proof of our result, are consequences of the properties of Normalization, Additivity and Homotopy Invariance.
Theorem 5.2 (uniqueness of the degree).
Let  be a real function on the family of admissible pairs satisfying the properties of Normalization, Additivity, and Homotopy Invariance. If
be a real function on the family of admissible pairs satisfying the properties of Normalization, Additivity, and Homotopy Invariance. If  is a nondegenerate pair, then
is a nondegenerate pair, then

Consequently, there exists at most one function on the family of admissible pairs satisfying the axioms for the degree of a tangent vector field, and this function, if it exists, must be integer valued.
Proof.
Consider first the case  . Let
. Let  be a nondegenerate pair in
be a nondegenerate pair in  and, for any
and, for any  , let
, let  be an isolating neighborhood of
be an isolating neighborhood of  . We may assume that the neighborhoods
. We may assume that the neighborhoods  are pairwise disjoint. Additivity and Localization together with Lemma 4.2 yield
are pairwise disjoint. Additivity and Localization together with Lemma 4.2 yield

Now the uniqueness of the degree of a tangent vector field on  follows immediately from Lemma 5.1.
follows immediately from Lemma 5.1.
Let us now consider the general case and denote by  the dimension of
the dimension of  . Let
. Let  be any open subset of
be any open subset of  which is diffeomorphic to
which is diffeomorphic to  and let
and let  be any diffeomorphism onto
be any diffeomorphism onto  . Denote by
. Denote by  the set of all pairs
the set of all pairs  which are admissible and such that
which are admissible and such that  . We claim that for any
. We claim that for any  one necessarily has
one necessarily has

To show this, denote by  the set of admissible pairs
the set of admissible pairs  with
with  and consider the map
and consider the map  defined by
defined by

Our claim means that the restriction  of
of  to
to  coincides with
coincides with  . Observe that
. Observe that  is invertible and
is invertible and

Moreover if two pairs  and
and  correspond under
correspond under  , then the sets
, then the sets  and
and  correspond under
correspond under  . It is also evident that the function
. It is also evident that the function  satisfies the axioms. Thus, by the first part of the proof, it coincides with the restriction
satisfies the axioms. Thus, by the first part of the proof, it coincides with the restriction  , and this implies our claim.
, and this implies our claim.
Now let  be a given nondegenerate pair in
be a given nondegenerate pair in  . Let
. Let  and let
and let  be
be  pairwise disjoint open subsets of
pairwise disjoint open subsets of  such that
such that  , for
, for  . Since any point of
. Since any point of  has a fundamental system of neighborhoods which are diffeomorphic to
has a fundamental system of neighborhoods which are diffeomorphic to  , we may assume that each
, we may assume that each  is diffeomorphic to
is diffeomorphic to  by a diffeomorphism
by a diffeomorphism  . Additivity and Localization yield
. Additivity and Localization yield

and, by the above claim, we get

By Lemma 4.2 and Remark 2.1

for  . Thus
. Thus

As in the case  , the uniqueness of the degree of a tangent vector field is now a consequence of Lemma 5.1.
, the uniqueness of the degree of a tangent vector field is now a consequence of Lemma 5.1.
References
Krasnosel'skiĭ MA: The Operator of Translation along the Trajectories of Differential Equations, Translations of Mathematical Monographs, vol. 19. American Mathematical Society, Providence, RI, USA; 1968:vi+294.
Krasnosel'skiĭ MA, Zabreĭko PP: Geometrical Methods of Nonlinear Analysis, Grundlehren der Mathematischen Wissenschaften. Volume 263. Springer, Berlin, Germany; 1984:xix+409.
Guillemin V, Pollack A: Differential Topology. Prentice-Hall, Englewood Cliffs, NJ, USA; 1974:xvi+222.
Hirsch MW: Differential Topology. Springer, New York, NY, USA; 1976:x+221. Graduate Texts in Mathematics, no. 33
Milnor JW: Topology from the Differentiable Viewpoint. The University Press of Virginia, Charlottesville, Va, USA; 1965:ix+65.
Tromba AJ: The Euler characteristic of vector fields on Banach manifolds and a globalization of Leray-Schauder degree. Advances in Mathematics 1978,28(2):148–173. 10.1016/0001-8708(78)90061-0
Amann H, Weiss SA: On the uniqueness of the topological degree. Mathematische Zeitschrift 1973, 130: 39–54. 10.1007/BF01178975
Führer L: Ein elementarer analytischer beweis zur eindeutigkeit des abbildungsgrades im
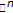 . Mathematische Nachrichten 1972, 54: 259–267. 10.1002/mana.19720540117
. Mathematische Nachrichten 1972, 54: 259–267. 10.1002/mana.19720540117Staecker PC: On the uniqueness of the coincidence index on orientable differentiable manifolds. Topology and Its Applications 2007,154(9):1961–1970. 10.1016/j.topol.2007.02.003
Furi M, Pera MP, Spadini M: On the uniqueness of the fixed point index on differentiable manifolds. Fixed Point Theory and Applications 2004,2004(4):251–259. 10.1155/S168718200440713X
Warner FW: Foundations of Differentiable Manifolds and Lie Groups, Graduate Texts in Mathematics. Volume 94. Springer, New York, NY, USA; 1983:ix+272.
Acknowledgment
The author is dedicated to Professor William Art Kirk for his outstanding contributions in the theory fixed points
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Furi, M., Pera, M. & Spadini, M. A Set of Axioms for the Degree of a Tangent Vector Field on Differentiable Manifolds. Fixed Point Theory Appl 2010, 845631 (2010). https://doi.org/10.1155/2010/845631
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/845631
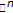 . Mathematische Nachrichten 1972, 54: 259–267. 10.1002/mana.19720540117
. Mathematische Nachrichten 1972, 54: 259–267. 10.1002/mana.19720540117