- Research Article
- Open access
- Published:
Regularization and Iterative Methods for Monotone Variational Inequalities
Fixed Point Theory and Applications volume 2010, Article number: 765206 (2009)
Abstract
We provide a general regularization method for monotone variational inequalities, where the regularizer is a Lipschitz continuous and strongly monotone operator. We also introduce an iterative method as discretization of the regularization method. We prove that both regularization and iterative methods converge in norm.
1. Introduction
Variational inequalities (VIs) have widely been studied (see the monographs [1–3]). A monotone variational inequality problem (VIP) is stated as finding a point  with the following property:
with the following property:

where  is a nonempty closed convex subset of a real Hilbert space
is a nonempty closed convex subset of a real Hilbert space  with inner product
with inner product  and norm
and norm  , respectively, and
, respectively, and  is a monotone operator in
is a monotone operator in  with domain
with domain  .
.
Recall that  is monotone if
is monotone if

A typical example of monotone operators is the subdifferential of a proper convex lower semicontinuous function.
Variational inequality problems are equivalent to fixed point problems. As a matter of fact,  solves VIP (1.1) if and only if
solves VIP (1.1) if and only if  solves the following fixed point problem (FPP), for any
solves the following fixed point problem (FPP), for any  ,
,

where  is the metric (or nearest point) projection from
is the metric (or nearest point) projection from  onto
onto  ; namely, for each
; namely, for each  ,
,  is the unique point in
is the unique point in  with the property
with the property

The equivalence between VIP (1.1) and FPP (1.3) is an immediate consequence of the following characterization of  :
:

The dual VIP of (1.1) is the following VIP:

The following equivalence between the dual VIP (1.6) and the primal VIP (1.1) plays a useful role in our regularization in Section 2.
Lemma 1.1 (cf. [4]).
Assume that  is monotone and weakly continuous along segments (i.e.,
is monotone and weakly continuous along segments (i.e.,  weakly as
weakly as  for
for  ), then the dual VIP (1.6) is equivalent to the primal VIP (1.1).
), then the dual VIP (1.6) is equivalent to the primal VIP (1.1).
To guarantee the existence and uniqueness of a solution of VIP (1.1), one has to impose conditions on the operator  . The following existence and uniqueness result is well known.
. The following existence and uniqueness result is well known.
Theorem 1.2.
If  is Lipschitz continuous and strongly monotone, then there exists one and only one solution to VIP (1.1).
is Lipschitz continuous and strongly monotone, then there exists one and only one solution to VIP (1.1).
However, if  fails to be Lipschitz continuous or strongly monotone, then the result of the above theorem is false in general. We will assume that
fails to be Lipschitz continuous or strongly monotone, then the result of the above theorem is false in general. We will assume that  is Lipschitz continuous, but do not assume strong monotonicity of
is Lipschitz continuous, but do not assume strong monotonicity of  . Thus, VIP (1.1) is ill-posed and regularization is needed; moreover, a solution is often sought through iteration methods.
. Thus, VIP (1.1) is ill-posed and regularization is needed; moreover, a solution is often sought through iteration methods.
In the special case where  is of the form
is of the form  , with
, with  being a nonexpansive mapping, regularization and iterative methods for VIP (1.1) have been investigated in literature; see, for example, [5–19]; work related to variational inequalities of monotone operators can be found in [20–25], and work related to iterative methods for nonexpansive mappings can be found in [26–33].
being a nonexpansive mapping, regularization and iterative methods for VIP (1.1) have been investigated in literature; see, for example, [5–19]; work related to variational inequalities of monotone operators can be found in [20–25], and work related to iterative methods for nonexpansive mappings can be found in [26–33].
The aim of this paper is to provide a regularization and its induced iteration method for VIP (1.1) in the general case. The paper is structured as follows. In the next section we present a general regularization method for VI (1.1) with the regularizer being a Lipschitz continuous and strongly monotone operator. In Section 3, by discretizing the implicit method of the regularization obtained in Section 2, we introduce an iteration process and prove its strong convergence. In the final section, Section 4, we apply the results obtained in Sections 2 and 3 to a convex minimization problem.
2. Regularization
Since VIP (1.1) is usually ill-posed, regularization is necessary, towards which we let  be a Lipschitz continuous, everywhere defined, strongly monotone, and single-valued operator. Consider the following regularized variational inequality problem:
be a Lipschitz continuous, everywhere defined, strongly monotone, and single-valued operator. Consider the following regularized variational inequality problem:

Since  is strongly monotone, VI (2.1) has a unique solution which is denoted by
is strongly monotone, VI (2.1) has a unique solution which is denoted by  . Indeed, VI (2.1) is equivalent to the fixed point equation
. Indeed, VI (2.1) is equivalent to the fixed point equation

where  , with
, with  .
.
To analyze more details of VI (2.1) (or its equivalent fixed point equation (2.2)), we need to impose more assumptions on the operators  and
and  . Assume that
. Assume that  and
and  are Lipschitz continuous with Lipschiz constants
are Lipschitz continuous with Lipschiz constants  , respectively. We also assume that
, respectively. We also assume that  is
is  -strongly monotone; namely, there is a constant
-strongly monotone; namely, there is a constant  satisfying the property
satisfying the property

Lemma 2.1.
If  is chosen in such a way that
is chosen in such a way that

then  is a contraction with contraction coefficient
is a contraction with contraction coefficient

Moreover, if

then

hence,  is a
is a  -contraction.
-contraction.
Proof.
Noticing that  is
is  -Lipschitzian and
-Lipschitzian and  -strongly monotone, we deduce that, for
-strongly monotone, we deduce that, for  ,
,

It turns out that if  satisfies (2.4), then
satisfies (2.4), then  is a contraction with coefficient given by the left side of (2.5).
is a contraction with coefficient given by the left side of (2.5).
Finally, it is straightforward that (2.7) holds provided that  satisfies (2.6).
satisfies (2.6).
Below we always assume that  satisfies (2.6) so that
satisfies (2.6) so that  is a
is a  -contraction from
-contraction from  into itself. Therefore, for such a choice of
into itself. Therefore, for such a choice of  ,
,  has a unique fixed point in
has a unique fixed point in  which is denoted as
which is denoted as  whose asymptotic behavior when
whose asymptotic behavior when  is given in the following result.
is given in the following result.
Theorem 2.2.
Assume that
(a) is monotone on
is monotone on  and weakly continuous along segments in
and weakly continuous along segments in  (i.e.,
(i.e.,  weakly as
weakly as  for
for  ),
),
(b) is
is  -monotone on
-monotone on  ,
,
(c)the solution set  of VI (1.1) is nonempty.
of VI (1.1) is nonempty.
For  , let
, let  be the unique solution of the regularized VIP (2.1). Then, as
be the unique solution of the regularized VIP (2.1). Then, as  ,
,  converges in norm to a point
converges in norm to a point  in
in  which is the unique solution of the VIP
which is the unique solution of the VIP

Therefore, if one takes  to be the identity operator, then the regularized solution
to be the identity operator, then the regularized solution  of the corresponding regularized VIP (2.1) converges in norm to the minimal norm point of the solution set
of the corresponding regularized VIP (2.1) converges in norm to the minimal norm point of the solution set  .
.
To prove Theorem 2.2, we first prove the boundedness of the net  .
.
Lemma 2.3.
Assume that  is monotone on
is monotone on  . Assume conditions (b) and (c) in Theorem 2.2. Then
. Assume conditions (b) and (c) in Theorem 2.2. Then  is bounded; indeed, for any
is bounded; indeed, for any  ,
,

Proof.
We have (2.1) holds for all  . In particular, for
. In particular, for  , we have
, we have

It turns out that

Since  is monotone and
is monotone and  is
is  -strongly monotone, we have
-strongly monotone, we have

Substituting them into (2.12) we obtain

However, since  ,
,  . We therefore get from (2.14) that
. We therefore get from (2.14) that

Now (2.10) follows immediately from (2.15).
Proof of Theorem 2.2.
Since  is bounded by Lemma 2.3, the set of weak limit points as
is bounded by Lemma 2.3, the set of weak limit points as  of the net
of the net  ,
,  , is nonempty. Pick a
, is nonempty. Pick a  and let
and let  be a null sequence in the interval
be a null sequence in the interval  such that
such that  weakly as
weakly as  . We first show that
. We first show that  . To see this we use the equivalent dual VI of (2.1):
. To see this we use the equivalent dual VI of (2.1):

Thus, we have, for all  and
and  ,
,

Taking the limit as  yields that
yields that

It turns out that  .
.
We next prove that the sequence  actually converges to
actually converges to  strongly. Replacing in (2.15)
strongly. Replacing in (2.15)  with
with  gives
gives

Now it is straightforward from (2.19) that the weak convergence to  of
of  implies strong convergence to
implies strong convergence to  of
of  .
.
The relation (2.15) particularly implies that, for  ,
,

which in turns implies that every point  solves the VIP
solves the VIP

or equivalently, the VIP

However, since  is strongly monotone, the solution to VIP (2.22) is unique. This has shown that the unique solution
is strongly monotone, the solution to VIP (2.22) is unique. This has shown that the unique solution  of VIP (2.22) is the strong limit of the net
of VIP (2.22) is the strong limit of the net  .
.
Finally, if  is the identity operator, then VIP (2.22) is reduced to
is the identity operator, then VIP (2.22) is reduced to

This is equivalent to

which immediately implies that  for all
for all  and hence
and hence  is the minimal norm of
is the minimal norm of  .
.
Remark 2.4.
In Theorem 2.2, we have proved that if the solution set  of VIP (1.1) is nonempty, then the net
of VIP (1.1) is nonempty, then the net  of the solutions of the regularized VIPs (2.1) is bounded (and hence converges in norm). The converse is indeed also true; that is, the boundedness of the net
of the solutions of the regularized VIPs (2.1) is bounded (and hence converges in norm). The converse is indeed also true; that is, the boundedness of the net  implies that the solution set
implies that the solution set  of VIP (1.1) is nonempty. As a matter of fact, suppose that
of VIP (1.1) is nonempty. As a matter of fact, suppose that  is bounded and
is bounded and  is a constant such that
is a constant such that  for all
for all  .
.
By Lemma 1.1, we have

Since  is bounded, we can easily see that every weak cluster point
is bounded, we can easily see that every weak cluster point  of the net
of the net  solves the VIP
solves the VIP

This is the dual VI to the primal VI (2.1); hence  is a solution of VI (2.1) by Lemma 1.1.
is a solution of VI (2.1) by Lemma 1.1.
3. Iterative Method
From the fixed point equation (2.2), it is natural to consider the following iteration method that generates a sequence  according to the recursion:
according to the recursion:

where the initial guess  is selected arbitrarily, and
is selected arbitrarily, and  and
and  are two sequences of positive numbers in
are two sequences of positive numbers in  . Put in another way,
. Put in another way,  is the unique solution in
is the unique solution in  of the following VIP:
of the following VIP:

Theorem 3.1.
Assume that
(a) is
is  -Lipschitz continuous and monotone on
-Lipschitz continuous and monotone on  ,
,
(b) is
is  -Lipschitz continuous and
-Lipschitz continuous and  -monotone on
-monotone on 
(c)the solution set  of VI (1.1) is nonempty.
of VI (1.1) is nonempty.
Assume in addition that
(i)
(ii) as
as  ,
,
(iii) ,
,
(iv) ,
,
then the sequence  generated by the algorithm (3.1) converges in norm to the unique solution of VI (2.9).
generated by the algorithm (3.1) converges in norm to the unique solution of VI (2.9).
To prove Theorem 3.1, we need a lemma below.
Lemma 3.2 (cf. [20]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  and
and  are real sequences such that
are real sequences such that
(i) for all
for all  , and
, and  ;
;
(ii)
then  .
.
Proof of Theorem 3.1.
Let  , where
, where  . By assumption (i) and Lemma 2.1,
. By assumption (i) and Lemma 2.1,  is a contraction and has a unique fixed point which is denoted by
is a contraction and has a unique fixed point which is denoted by  . Moreover, by Theorem 2.2,
. Moreover, by Theorem 2.2,  converges in norm to the unique solution
converges in norm to the unique solution  of VI (2.9). Therefore, it suffices to prove that
of VI (2.9). Therefore, it suffices to prove that  as
as  .
.
To see this, observing that  is a
is a  -contraction, we obtain
-contraction, we obtain

However, we have

Since  is bounded, it turns out that, for an appropriate constant
is bounded, it turns out that, for an appropriate constant  ,
,

Substituting (3.6) into (3.4) and setting  , we get
, we get

where

with  . Assumptions (iii) and (iv) assure that
. Assumptions (iii) and (iv) assure that  and
and  as
as  , respectively. Therefore, we can apply lemma to (3.7) to conclude that
, respectively. Therefore, we can apply lemma to (3.7) to conclude that  ; hence,
; hence,  in norm.
in norm.
Remark 3.3.
Assume  satisfy
satisfy  , then it is not hard to see that for an appropriate constant
, then it is not hard to see that for an appropriate constant  ,
,

satisfy the assumptions (i)–(iv) of Theorem 3.1.
4. Application
Consider the constrained convex minimization problem:

where  is a closed convex subset of a real Hilbert space
is a closed convex subset of a real Hilbert space  and
and  is a real-valued convex function. Assume that
is a real-valued convex function. Assume that  is continuously differentiable with a Lipschitz continuous gradient:
is continuously differentiable with a Lipschitz continuous gradient:

where  is a constant.
is a constant.
It is known that the minimization (4.1) is equivalent to the variational inequality problem:

Therefore, applying Theorems 2.2 and 3.1, we get the following result.
Theorem 4.1.
Assume the Lipschitz continuity (4.2) for the gradient  .
.
-
(a)
For
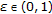 , let
, let 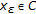 be the unique solution of the regularized VIP
be the unique solution of the regularized VIP

Equivalently,  is the unique solution in
is the unique solution in  of the regularized minimization problem:
of the regularized minimization problem:

Then, as  ,
,  remains bounded if and only if (4.1) has a solution, and in this case,
remains bounded if and only if (4.1) has a solution, and in this case,  converges in norm to the minimal norm solution of (4.1).
converges in norm to the minimal norm solution of (4.1).
-
(b)
Assume that (4.1) has a solution. Assume in addition that
(i)
(ii) as
as  ,
,
(iii) ,
,
(iv)
Starting  , one defines
, one defines  by the iterative algorithm
by the iterative algorithm

Then  converges in norm to the minimum-norm solution of the constrained minimization problem (4.1).
converges in norm to the minimum-norm solution of the constrained minimization problem (4.1).
Proof.
Apply Theorems 2.2 and 3.1 to the case where  and
and  is the identity operator to get the conclusions in (a) and (b).
is the identity operator to get the conclusions in (a) and (b).
References
Baiocchi C, Capelo A: Variational and Quasivariational Inequalities: Applications to Free Boundary Problems, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1984:ix+452.
Giannessi F, Maugeri A: Variational Inequalities and Network Equilibrium Problems. Plenum Press, New York, NY, USA; 1995.
Kinderlehrer D, Stampacchia G: An Introduction to Variational Inequalities and Their Applications, Pure and Applied Mathematics. Volume 88. Academic Press, New York, NY, USA; 1980:xiv+313.
Konnov IV, Schaible S: Duality for equilibrium problems under generalized monotonicity. Journal of Optimization Theory and Applications 2000,104(2):395–408. 10.1023/A:1004665830923
Ceng L-C, Ansari QH, Yao J-C: Mann-type steepest-descent and modified hybrid steepest-descent methods for variational inequalities in Banach spaces. Numerical Functional Analysis and Optimization 2008,29(9–10):987–1033. 10.1080/01630560802418391
Zeng LC, Schaible S, Yao J-C: Hybrid steepest descent methods for zeros of nonlinear operators with applications to variational inequalities. Journal of Optimization Theory and Applications 2009,141(1):75–91. 10.1007/s10957-008-9501-4
Ceng L-C, Xu HK, Yao J-C: A hybrid steepest-descent method for variational inequalities in Hilbert spaces. Applicable Analysis 2008,87(5):575–589. 10.1080/00036810802140608
Chen R, Su Y, Xu HK: Regularization and iteration methods for a class of monotone variational inequalities. Taiwanese Journal of Mathematics 2009,13(2B):739–752.
Lemaire B, Salem ChOA: From fixed-point regularization to constraint decomposition in variational inequalities. In Proceedings of the 9th Belgian-French-German Conference on Optimization, September 1998, Namur, Belgium, Lecture Notes in Economic and Mathematical Systems. Volume 481. Springer; 250–259.
Lu X, Xu H-K, Yin X: Hybrid methods for a class of monotone variational inequalities. Nonlinear Analysis: Theory, Methods & Applications 2009,71(3–4):1032–1041. 10.1016/j.na.2008.11.067
Maingé P-E, Moudafi A: Strong convergence of an iterative method for hierarchical fixed-point problems. Pacific Journal of Optimization 2007,3(3):529–538.
Marino G, Xu HK: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006,318(1):43–52. 10.1016/j.jmaa.2005.05.028
Marino G, Xu HK: Explicit hierarchical fixed point approach to variational inequalities. preprint
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Moudafi A, Maingé P-E: Towards viscosity approximations of hierarchical fixed-point problems. Fixed Point Theory and Applications 2006, 2006:-10.
Salem ChOA: Approximation de points fixes d'une contraction, Ph.D. thesis. Université Montpellier, Cedex, France; 1998.
Tam NN, Yao J-C, Yen ND: Solution methods for pseudomonotone variational inequalities. Journal of Optimization Theory and Applications 2008,138(2):253–273. 10.1007/s10957-008-9376-4
Wong NC, Sahu DR, Yao J-C: Solving variational inequalities involving nonexpansive type mappings. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4732–4753. 10.1016/j.na.2007.11.025
Yao J-C: Variational inequalities with generalized monotone operators. Mathematics of Operations Research 1994,19(3):691–705. 10.1287/moor.19.3.691
Xu HK: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002,66(1):240–256. 10.1112/S0024610702003332
Xu HK: Another control condition in an iterative method for nonexpansive mappings. Bulletin of the Australian Mathematical Society 2002,65(1):109–113. 10.1017/S0004972700020116
Xu HK: Remarks on an iterative method for nonexpansive mappings. Communications on Applied Nonlinear Analysis 2003,10(1):67–75.
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Xu HK: Viscosity method for hierarchical fixed point approach to variational inequalities. Taiwanese Journal of Mathematics 2010.,14(2):
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, Stud. Comput. Math.. Volume 8. North-Holland, Amsterdam, The Netherlands; 2001:473–504.
Browder FE: Convergence of approximants to fixed points of nonexpansive non-linear mappings in Banach spaces. Archive for Rational Mechanics and Analysis 1967, 24: 82–90.
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Lions P-L: Approximation de points fixes de contractions. Comptes Rendus de l'Académie des Sciences de Paris, Série. A-B 1977,284(21):A1357-A1359.
Reich S: Strong convergence theorems for resolvents of accretive operators in Banach spaces. Journal of Mathematical Analysis and Applications 1980,75(1):287–292. 10.1016/0022-247X(80)90323-6
Reich S: Approximating fixed points of nonexpansive mappings. PanAmerican Mathematical Journal 1994,4(2):23–28.
Shioji N, Takahashi W: Strong convergence of approximated sequences for nonexpansive mappings in Banach spaces. Proceedings of the American Mathematical Society 1997,125(12):3641–3645. 10.1090/S0002-9939-97-04033-1
Wittmann R: Approximation of fixed points of nonexpansive mappings. Archiv der Mathematik 1992,58(5):486–491. 10.1007/BF01190119
Xu HK: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Acknowledgments
The authors are grateful to the anonymous referees for their comments and suggestions which improved the presentation of this paper. This paper is dedicated to Professor William Art Kirk for his significant contributions to fixed point theory. The first author was supported in part by a fund (Grant no. 2008ZG052) from Zhejiang Administration of Foreign Experts Affairs. The second author was supported in part by NSC 97-2628-M-110-003-MY3, and by DGES MTM2006-13997-C02-01.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, X., Xu, HK. Regularization and Iterative Methods for Monotone Variational Inequalities. Fixed Point Theory Appl 2010, 765206 (2009). https://doi.org/10.1155/2010/765206
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/765206
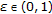 , let
, let 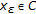 be the unique solution of the regularized VIP
be the unique solution of the regularized VIP