- Research Article
- Open access
- Published:
Robustness of Mann Type Algorithm with Perturbed Mapping for Nonexpansive Mappings in Banach Spaces
Fixed Point Theory and Applications volume 2010, Article number: 734181 (2010)
Abstract
The purpose of this paper is to study the robustness of Mann type algorithm in the sense that approximately perturbed mapping does not alter the convergence of Mann type algorithm. It is proven that Mann type algorithm with perturbed mapping  remains convergent in a Banach space setting where
remains convergent in a Banach space setting where  ,
,  a nonexpansive mapping,
a nonexpansive mapping,  ,
,  , errors and
, errors and  a strongly accretive and strictly pseudocontractive mapping.
a strongly accretive and strictly pseudocontractive mapping.
1. Introduction
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  , and
, and  a nonexpansive mapping (i.e.,
a nonexpansive mapping (i.e.,  for all
for all  ). We use
). We use  to denote the set of fixed points of
to denote the set of fixed points of  ; that is,
; that is,  . Throughout this paper it is assumed that
. Throughout this paper it is assumed that  . Construction of fixed points of nonlinear mappings is an important and active research area. In particular, iterative methods for finding fixed points of nonexpansive mappings have received vast investigation since these methods find applications in a variety of applied areas of variational inequality problems, equilibrium problems, inverse problems, partial differential equations, image recovery, and signal processing (see, e.g., [1–17]).
. Construction of fixed points of nonlinear mappings is an important and active research area. In particular, iterative methods for finding fixed points of nonexpansive mappings have received vast investigation since these methods find applications in a variety of applied areas of variational inequality problems, equilibrium problems, inverse problems, partial differential equations, image recovery, and signal processing (see, e.g., [1–17]).
In 1953, Mann [18] introduced an iterative algorithm which is now referred to as Mann's algorithm. Most of the literature deals with the special case of the general Mann's algorithm; that is, for an arbitrary initial guess  , the sequence
, the sequence  is generated by the recursive manner
is generated by the recursive manner

where  is a convex subset of a Banach space
is a convex subset of a Banach space  is a mapping and
is a mapping and  is a sequence in the interval
is a sequence in the interval  . It is well known that Mann's algorithm can be employed to approximate fixed points of nonexpansive mappings and zeros of (strongly) accretive mappings in Hilbert spaces and Banach spaces. Many convergence theorems have been announced and published by a large number of authors. A typical convergence result in connection with the Mann's algorithm is the following theorem proved by Ishikawa [19].
. It is well known that Mann's algorithm can be employed to approximate fixed points of nonexpansive mappings and zeros of (strongly) accretive mappings in Hilbert spaces and Banach spaces. Many convergence theorems have been announced and published by a large number of authors. A typical convergence result in connection with the Mann's algorithm is the following theorem proved by Ishikawa [19].
Theorem IS (see [19])
Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  and let
and let  be a nonexpansive mapping. Let
be a nonexpansive mapping. Let  be a real sequence satisfying the following control conditions:
be a real sequence satisfying the following control conditions:
(a) ;
;
(b) .
.
Let  be defined by (1.1) such that
be defined by (1.1) such that  for all
for all  . If
. If  is bounded then
is bounded then  as
as  .
.
The interest and importance of Theorem IS lie in the fact that strong or weak convergence of the sequence  can be achieved under certain appropriate assumptions imposed on the mapping
can be achieved under certain appropriate assumptions imposed on the mapping  , the domain
, the domain  or the space
or the space  . In an infinite-dimensional space
. In an infinite-dimensional space  , Mann's algorithm has only weak convergence, in general. In fact, it is known that if the sequence
, Mann's algorithm has only weak convergence, in general. In fact, it is known that if the sequence  is such that
is such that  , then Mann's algorithm converges weakly to a fixed point of
, then Mann's algorithm converges weakly to a fixed point of  provided that the underlying space
provided that the underlying space  is a Hilbert space or more general, a uniformly convex Banach space which has a Fréchet differentiable norm or satisfies Opial's property. See, for example, [20, 21].
is a Hilbert space or more general, a uniformly convex Banach space which has a Fréchet differentiable norm or satisfies Opial's property. See, for example, [20, 21].
The study of the robustness of Mann's algorithm is initiated by Combettes [22] where he considered a parallel projection method algorithm in signal synthesis (design and recovery) problems in a real Hilbert space  as follows:
as follows:

where for each  ,
,  is the (nearest point) projection of a signal
is the (nearest point) projection of a signal  onto a closed convex subset
onto a closed convex subset  of
of  [23] (
[23] ( is interpreted as the
is interpreted as the  th constraint set of the signals),
th constraint set of the signals),  is a sequence of relaxation parameters in
is a sequence of relaxation parameters in  are strictly positive weights such that
are strictly positive weights such that  , and
, and  stands for the error made in computing the projection onto
stands for the error made in computing the projection onto  at iteration
at iteration  . Then he proved the following robustness result of algorithm (1.2).
. Then he proved the following robustness result of algorithm (1.2).
Theorem 1.1 (see [22]).
Assume  . Assume also
. Assume also
(i)
(ii) .
.
Then the sequence  generated by (1.2) converges weakly to a point in
generated by (1.2) converges weakly to a point in  .
.
Define a mapping  by
by

and put

Since  is a projection, the mapping
is a projection, the mapping  is nonexpansive. Thus
is nonexpansive. Thus  and algorithm (1.2) can be rewritten as
and algorithm (1.2) can be rewritten as

where  is given by (1.3). Note that
is given by (1.3). Note that  can be written as
can be written as  and thus
and thus  is nonexpansive. Note also that
is nonexpansive. Note also that  . Furthermore, conditions (i) and (ii) in Theorem 1.1 can be stated as
. Furthermore, conditions (i) and (ii) in Theorem 1.1 can be stated as

 .
.
Very early, some authors had considered Mann iterations in the setting of uniformly convex Banach spaces and established strong and weak convergence results for Mann iterations; see, e.g., [24, 25]. Recently, Kim and Xu [26] studied the robustness of Mann's algorithm for nonexpansive mappings in Banach spaces and extended Combettes' robustness result (Theorem 1.1 above) for projections from Hilbert spaces to the setting of uniformly convex Banach spaces.
Theorem 1.2 (see [26, Theorem 3.3]).
Assume that  is a uniformly convex Banach space. Assume, in addition, that either
is a uniformly convex Banach space. Assume, in addition, that either  has the KK- property or
has the KK- property or  satisfies Opial's property. Let
satisfies Opial's property. Let  be a nonexpansive mapping such that
be a nonexpansive mapping such that  . Given an initial guess
. Given an initial guess  . Let
. Let  be generated by the following perturbed Mann's algorithm:
be generated by the following perturbed Mann's algorithm:

where  and
and  satisfy the following properties:
satisfy the following properties:
(i) ,
,
(ii) .
.
Then the sequence  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
Further, Kim and Xu [26] also extended the robustness to nonexpansive mappings which are defined on subsets of a Hilbert space and to accretive operators.
Theorem 1.3 (see [26, Theorem 4.1]).
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  and
and  a nonexpansive mapping with
a nonexpansive mapping with  . Let
. Let  be generated from an arbitrary
be generated from an arbitrary  via one of the following algorithms (1.7) and (1.7):
via one of the following algorithms (1.7) and (1.7):

where the sequences  and
and  are such that
are such that
(i) ,
,
(ii) .
.
Then  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
Theorem 1.4 (see [26, Theorem 5.1]).
Let  be a uniformly convex Banach space. Assume in addition that either
be a uniformly convex Banach space. Assume in addition that either  has the KK- property or
has the KK- property or  satisfies Opial's property. Let
satisfies Opial's property. Let  be an
be an  -accretive operator in
-accretive operator in  such that
such that  . Moreover, assume that
. Moreover, assume that  and
and  satisfy the following properties:
satisfy the following properties:
(i) ;
;
(ii) ;
;
(iii) , where
, where  and
and  are two constants;
are two constants;
(iv) .
.
Then the sequence  generated from an arbitrary
generated from an arbitrary  by
by

converges weakly to a point of  .
.
Let  be a real reflexive Banach space. Let
be a real reflexive Banach space. Let  be a nonexpansive mapping with
be a nonexpansive mapping with  . Assume that
. Assume that  is
is  -strongly accretive and
-strongly accretive and  -strictly pseudocontractive with
-strictly pseudocontractive with  where
where  . In this paper, inspired by Combettes' robustness result (Theorem 1.1 above) and Kim and Xu's robustness result (Theorem 1.2 above) we will consider the robustness of Mann type algorithm with perturbed mapping, which generates, from an arbitrary initial guess
. In this paper, inspired by Combettes' robustness result (Theorem 1.1 above) and Kim and Xu's robustness result (Theorem 1.2 above) we will consider the robustness of Mann type algorithm with perturbed mapping, which generates, from an arbitrary initial guess  , a sequence
, a sequence  by the recursive manner
by the recursive manner

where  and
and  are sequences in
are sequences in  and in
and in  , respectively, such that
, respectively, such that
(i) ;
;
(ii) ;
;
(iii) .
.
More precisely, we will prove under conditions (i)–(iii) the weak convergence of the algorithm (1.9) in a uniformly convex Banach space  which either has the KK- property or satisfies Opial's property. This theorem extends Kim and Xu's robustness result (Theorem 1.2 above) from Mann's algorithm (1.6) with errors to Mann type algorithm (1.9) with perturbed mapping
which either has the KK- property or satisfies Opial's property. This theorem extends Kim and Xu's robustness result (Theorem 1.2 above) from Mann's algorithm (1.6) with errors to Mann type algorithm (1.9) with perturbed mapping  . On the other hand, we also extend Kim and Xu's robustness results (Theorems 1.3 and 1.4 above) for nonexpansive mappings which are defined on subsets of a Hilbert space and accretive operators in a uniformly convex Banach space from Mann's algorithm with errors to Mann type algorithm with perturbed mapping.
. On the other hand, we also extend Kim and Xu's robustness results (Theorems 1.3 and 1.4 above) for nonexpansive mappings which are defined on subsets of a Hilbert space and accretive operators in a uniformly convex Banach space from Mann's algorithm with errors to Mann type algorithm with perturbed mapping.
Throughout this paper, we use the following notations:
(i) stands for weak convergence and
stands for weak convergence and  for strong convergence,
for strong convergence,
(ii) denotes the weak
denotes the weak  -limit set of
-limit set of  .
.
2. Preliminaries
Let  be a real Banach space. Recall that the norm of
be a real Banach space. Recall that the norm of  is said to be Fréchet differentiable if, for each
is said to be Fréchet differentiable if, for each  , the unit sphere of
, the unit sphere of  , the limit
, the limit

exists and is attained uniformly in  . In this case, we have
. In this case, we have

for all  , where
, where  is the normalized duality map from
is the normalized duality map from  to
to  defined by
defined by

 is the duality pairing between
is the duality pairing between  and
and  , and
, and  is a function defined on
is a function defined on  such that
such that  . Examples of Banach spaces which have a Fréchet differentiable norm include
. Examples of Banach spaces which have a Fréchet differentiable norm include  and
and  for
for  (these spaces are actually uniformly smooth).
(these spaces are actually uniformly smooth).
It is known that a Banach space  is Fréchet differentiable if and only if the duality map
is Fréchet differentiable if and only if the duality map  is single-valued and norm-to-norm continuous.
is single-valued and norm-to-norm continuous.
We need the concept of the KK-property. A Banach space  is said to have the KK-property (the Kadec-Klee property) if, for any sequence
is said to have the KK-property (the Kadec-Klee property) if, for any sequence  in
in  , the conditions
, the conditions  and
and  imply that
imply that  . It is known [27, Remark 3.2] that the dual space of a reflexive Banach space with a Fréchet differentiable norm has the KK-property.
. It is known [27, Remark 3.2] that the dual space of a reflexive Banach space with a Fréchet differentiable norm has the KK-property.
Recall now that  satisfies Opial's property [28] provided that, for each sequence
satisfies Opial's property [28] provided that, for each sequence  in
in  , the condition
, the condition  implies
implies

It is known [28] that each  enjoys this property, while
enjoys this property, while  does not unless
does not unless  . It is known [29] that any separable Banach space can be equivalently renormed so that it satisfies Opial's property.
. It is known [29] that any separable Banach space can be equivalently renormed so that it satisfies Opial's property.
Recall that a Banach space  is said to be uniformly convex if, for each
is said to be uniformly convex if, for each  , the modulus of convexity
, the modulus of convexity  of
of  defined by
defined by

is positive.
We need an inequality characterization of uniform convexity.
Lemma 2.1 (see [30]).
Given a number  . A real Banach space
. A real Banach space  is uniformly convex if and only if there exists a continuous strictly increasing function
is uniformly convex if and only if there exists a continuous strictly increasing function  , such that
, such that

for all  and
and  such that
such that  and
and  .
.
A mapping  with domain
with domain  and range
and range  in
in  is called
is called  -strongly accretive if for each
-strongly accretive if for each  ,
,

for some  .
.  is called
is called  -strictly pseudocontractive if for each
-strictly pseudocontractive if for each  ,
,

for some  . It is easy to see that (2.8) can be rewritten as
. It is easy to see that (2.8) can be rewritten as

The following proposition will be used frequently throughout this paper. For the sake of completeness, we include its proof.
Proposition 2.2.
Let  be a real Banach space and
be a real Banach space and  a mapping.
a mapping.
(i)If  is a
is a  -strictly pseudocontractive, then
-strictly pseudocontractive, then  is Lipschitz continuous with constant
is Lipschitz continuous with constant 
(ii)If  is
is  -strongly accretive and
-strongly accretive and  -strictly pseudocontractive with
-strictly pseudocontractive with  , then for each fixed
, then for each fixed  , the mapping
, the mapping  has the following property:
has the following property:

Proof.
-
(i)
From (2.9), we derive
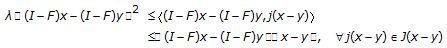 (2.11)
(2.11)
which implies that

Thus

and so  is Lipschitz continuous with constant
is Lipschitz continuous with constant  .
.
-
(ii)
From (2.8) and (2.9), we obtain

Since  , we have
, we have

Consequently, for each fixed  , we have
, we have

This shows that inequality (2.10) holds.
Proposition 2.3.
Let  be a uniformly convex Banach space and
be a uniformly convex Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  .
.
(i)Reference [31] (demiclosedness principle). If  is a nonexpansive mapping and if
is a nonexpansive mapping and if  is a sequence in
is a sequence in  such that
such that  and
and  , then
, then  .
.
(ii)Reference [32]. If  is also bounded, then there exists a continuous, strictly increasing, and convex function
is also bounded, then there exists a continuous, strictly increasing, and convex function  (depending only on the diameter of
(depending only on the diameter of  ) with
) with  and such that
and such that

for all  , and nonexpansive mappings
, and nonexpansive mappings  .
.
We also use the following elementary lemma.
Lemma 2.4 (see [33]).
Let  and
and  be sequences of nonnegative real numbers such that
be sequences of nonnegative real numbers such that  and
and  for all
for all  . Then
. Then  exists.
exists.
3. Robustness of Mann Type Algorithm with Perturbed Mapping
Let  be a real reflexive Banach space. Let
be a real reflexive Banach space. Let  be a nonexpansive mapping with
be a nonexpansive mapping with  . Assume that
. Assume that  is
is  -strongly accretive and
-strongly accretive and  -strictly pseudocontractive with
-strictly pseudocontractive with  . We now discuss the robustness of Mann type algorithm with perturbed mapping, which generates, from an initial guess
. We now discuss the robustness of Mann type algorithm with perturbed mapping, which generates, from an initial guess  , a sequence
, a sequence  as follows:
as follows:

where  and
and  are sequences in
are sequences in  and in
and in  , respectively, such that
, respectively, such that
(i) ;
;
(ii) ;
;
(iii) .
.
We remark that Mann type algorithm with perturbed mapping is based on Mann iteration method and steepest-descent method. Indeed, in algorithm (3.1), one iteration step " " is taken from Mann iteration method, and another iteration step "
" is taken from Mann iteration method, and another iteration step " " is taken from steepest-descent method.
" is taken from steepest-descent method.
We first discuss some properties of algorithm (3.1).
Lemma 3.1.
Let  be generated by algorithm (3.1) and let
be generated by algorithm (3.1) and let  Then
Then  exists.
exists.
Proof.
We have

The conclusion of the lemma is a consequence of Lemma 2.4.
Proposition 3.2.
Let  be a uniformly convex Banach space.
be a uniformly convex Banach space.
(i)For all  and
and  ,
,  exists.
exists.
(ii)If, in addition, the dual space  of
of  has the
has the  -property, then the weak
-property, then the weak  -limit set of
-limit set of  ,
,  , is a singleton.
, is a singleton.
Proof.
-
(i)
For integers
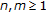 , define the mappings
, define the mappings  and
and 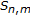 as follows:
as follows:

and  . It is easy to see that
. It is easy to see that  . First, let us show that
. First, let us show that  and
and  are nonexpansive. Indeed, for all
are nonexpansive. Indeed, for all  , using Proposition 2.2 no. (ii) we have
, using Proposition 2.2 no. (ii) we have

Thus  is nonexpansive (due to
is nonexpansive (due to  ) and so is
) and so is  .
.
Second, let us show that for each  ,
,

Indeed, whenever  , we have
, we have

This implies that inequality (3.5) holds for  . Assume that inequality (3.5) holds for some
. Assume that inequality (3.5) holds for some  . Consider the case of
. Consider the case of  . Observe that
. Observe that

This shows that inequality (3.5) holds for the case of  . Thus, by induction, we know that inequality (3.5) holds for all
. Thus, by induction, we know that inequality (3.5) holds for all  .
.
Now set

By Proposition 2.3 no. (ii) and noticing inequality (3.5) we deduce that

Therefore,

Since  exists and
exists and  and
and  are convergent, we conclude from (3.10) that
are convergent, we conclude from (3.10) that

Also, since, for all  ,
,

it follows from (3.11) and (3.12) that  exists.
exists.
-
(ii)
This is Lemma 3.2 of [27].
Now we can state and prove the main result of this section.
Theorem 3.3.
Assume that  is a uniformly convex Banach space. Assume, in addition, that either
is a uniformly convex Banach space. Assume, in addition, that either  has the
has the  -property or
-property or  satisfies Opial's property. Let
satisfies Opial's property. Let  be a nonexpansive mapping such that
be a nonexpansive mapping such that  and
and 
 -strongly accretive and
-strongly accretive and  -strictly pseudocontractive with
-strictly pseudocontractive with  . Given an initial guess
. Given an initial guess  . Let
. Let  be generated by the following Mann type algorithm with perturbed mapping
be generated by the following Mann type algorithm with perturbed mapping 

where  and
and  satisfy the following properties:
satisfy the following properties:
(i) ;
;
(ii) ;
;
(iii) .
.
Then the sequence  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
Proof.
Fix  and select a number
and select a number  large enough so that
large enough so that  for all
for all  . Let
. Let  satisfy
satisfy  for all
for all  . By Lemma 2.1, we have
. By Lemma 2.1, we have

It follows that

This implies that

In particular,  . Due to condition (i), we must have that
. Due to condition (i), we must have that  . Hence
. Hence

However, since

we have

and, by Lemma 2.4,  exists and hence, by (3.17),
exists and hence, by (3.17),

Notice that, by the demiclosedness principle of  , we obtain
, we obtain

Hence to prove that  converges weakly to a fixed point of
converges weakly to a fixed point of  , it suffices to show that
, it suffices to show that  is a singleton. We distinguish two cases. First assume that
is a singleton. We distinguish two cases. First assume that  has the KK-property. Then that
has the KK-property. Then that  is a singleton is guaranteed by Proposition 3.2 no. (ii).
is a singleton is guaranteed by Proposition 3.2 no. (ii).
Next assume that  satisfies Opial's property. Take
satisfies Opial's property. Take  and let
and let  and
and  be subsequences of
be subsequences of  such that
such that  and
and  , respectively. If
, respectively. If  , we reach the following contradiction:
, we reach the following contradiction:

This shows that  is a singleton. The proof is therefore complete.
is a singleton. The proof is therefore complete.
4. The Case Where Mappings Are Defined on Subsets
We observe that if the domain  is a proper closed convex subset
is a proper closed convex subset  of
of  , then the vectors
, then the vectors  and
and  may not belong to
may not belong to  . In this case the next iterate
. In this case the next iterate  may not be well defined by (3.13). In order to consider this situation, we will use the nearest projection
may not be well defined by (3.13). In order to consider this situation, we will use the nearest projection  and for the projection to be nonexpansive, we have to restrict our spaces to be Hilbert spaces.
and for the projection to be nonexpansive, we have to restrict our spaces to be Hilbert spaces.
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Given a closed convex subset
. Given a closed convex subset  of
of  . Recall that the (nearest point) projection
. Recall that the (nearest point) projection  from
from  onto
onto  assigns each point
assigns each point  with its (unique) nearest point in
with its (unique) nearest point in  which is denoted by
which is denoted by  . Namely,
. Namely,  is the unique point in
is the unique point in  with the property
with the property

Note that  is nonexpansive.
is nonexpansive.
Let  be a nonexpansive mapping with
be a nonexpansive mapping with  and
and 
 -strongly monotone and
-strongly monotone and  -strictly pseudocontractive with
-strictly pseudocontractive with  . Starting with
. Starting with  and after
and after  in
in  is defined, we have two ways to define the next iterate
is defined, we have two ways to define the next iterate  : either applying the projection
: either applying the projection  to the vectors
to the vectors  and
and  and defining
and defining  as the convex combination of
as the convex combination of  and
and  , or projecting a convex combination of
, or projecting a convex combination of  and
and  onto
onto  to define
to define  . More precisely, we define
. More precisely, we define  as follows:
as follows:

or

Theorem 4.1.
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  . Let
. Let  be a nonexpansive mapping with
be a nonexpansive mapping with  and
and 
 -strongly monotone and
-strongly monotone and  -strictly pseudocontractive with
-strictly pseudocontractive with  . Let
. Let  be generated by either (4.2) or (4.3) where the sequences
be generated by either (4.2) or (4.3) where the sequences  and
and  are such that
are such that
(i) ;
;
(ii) ;
;
(iii) .
.
Then  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
Proof.
Given  . Assume that
. Assume that  is generated by (4.2). Then
is generated by (4.2). Then

Hence  exists; in particular,
exists; in particular,  is bounded. Let
is bounded. Let  be a constant such that
be a constant such that  for all
for all  .
.
We compute

That is,

This implies that

In particular (noticing assumption (i)),

We also have

Moreover, noticing

we have

Similarly, if  is generated by algorithm (4.3), then relations (4.4)–(4.11) still hold.
is generated by algorithm (4.3), then relations (4.4)–(4.11) still hold.
It is now readily seen that (4.11) together with Lemma 2.4 implies that  exists, which together with (4.8) further implies that
exists, which together with (4.8) further implies that

Equation (4.12) implies that  , due to the demiclosedness principle. Finally, repeating the last part of the proof of Theorem 3.3 in the case of Opial's property, we see that
, due to the demiclosedness principle. Finally, repeating the last part of the proof of Theorem 3.3 in the case of Opial's property, we see that  converges weakly to a fixed point of
converges weakly to a fixed point of  . The proof is therefore complete.
. The proof is therefore complete.
Finally in this section, we consider the case of accretive operators. Recall that a multivalued operator  with domain
with domain  and range
and range  in a Banach space
in a Banach space  is said to be accretive if, for each
is said to be accretive if, for each  and
and  , there is
, there is  such that
such that

where  is the duality map from
is the duality map from  to the dual space
to the dual space  . An accretive operator
. An accretive operator  is
is  -accretive if
-accretive if  for all
for all  .
.
Denote by  the zero set of
the zero set of  ; that is,
; that is,

Throughout the rest of this paper it is always assumed that  is
is  -accretive and
-accretive and  is nonempty.
is nonempty.
Denote by  the resolvent of
the resolvent of  for
for  :
:

It is known that  is a nonexpansive mapping from
is a nonexpansive mapping from  to
to  which will be assumed convex (this is so if
which will be assumed convex (this is so if  is uniformly convex). It is also known that
is uniformly convex). It is also known that  for
for  .
.
Now consider the problem of finding a zero of an  -accretive operator
-accretive operator  in a Banach space
in a Banach space  ,
,

We will study the convergence of the following algorithm:

where  is a perturbed mapping, the initial guess
is a perturbed mapping, the initial guess  is arbitrary,
is arbitrary,  and
and  are two sequences in
are two sequences in  is a sequence of positive numbers, and
is a sequence of positive numbers, and  is an error sequence in
is an error sequence in  .
.
Theorem 4.2.
Let  be a uniformly convex Banach space. Assume in addition that either
be a uniformly convex Banach space. Assume in addition that either  has the
has the  -property or
-property or  satisfies Opial's property. Let
satisfies Opial's property. Let  be an
be an  -accretive operator in
-accretive operator in  such that
such that  and let
and let  be
be  -strongly accretive and
-strongly accretive and  -strictly pseudocontractive with
-strictly pseudocontractive with  . Moreover, assume that
. Moreover, assume that  and
and  satisfy the following properties:
satisfy the following properties:
(i) ;
;
(ii) ;
;
(iii) ;
;
(iv) , where
, where  and
and  are two constants;
are two constants;
(v) .
.
Then the sequence  generated by algorithm (4.17) converges weakly to a point of
generated by algorithm (4.17) converges weakly to a point of  .
.
Proof.
The proof is a refinement of that of Theorem 3.3 given in Section 3 and [34, Theorem 3.3] together with Proposition 3.2. So we only sketch it.
Let  . By (4.17), we have
. By (4.17), we have

By Lemma 2.4, we see that  exists.
exists.
With slight modifications of the proof of Theorem 3.3 (replacing  by
by  ), we can obtain that
), we can obtain that

Now noticing

and letting  for all
for all  , we deduce that
, we deduce that

By mimicking the proof of Theorem 3.3 in [34], we can show that, in the case of  ,
,

and in the case of  ,
,

where  is such that
is such that  for all
for all  . In either case we conclude from (4.22) and (4.23) that
. In either case we conclude from (4.22) and (4.23) that  satisfies
satisfies

where  fulfills
fulfills  . By Lemma 2.4, (4.24) implies that
. By Lemma 2.4, (4.24) implies that  (
( ) exists. This together with the assumption (iv) and (4.19) implies that
) exists. This together with the assumption (iv) and (4.19) implies that  . So, by Lemma 3.3 in [34], we have
. So, by Lemma 3.3 in [34], we have

By the demiclosedness principle, (4.25) ensures that  . Repeating the last part of the proof of Theorem 3.3, we conclude that
. Repeating the last part of the proof of Theorem 3.3, we conclude that  converges weakly to a point of
converges weakly to a point of  .
.
References
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Byrne C: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Problems 2004,20(1):103–120. 10.1088/0266-5611/20/1/006
Engl HW, Leitão A: A Mann iterative regularization method for elliptic Cauchy problems. Numerical Functional Analysis and Optimization 2001,22(7–8):861–884. 10.1081/NFA-100108313
Engl HW, Scherzer O: Convergence rates results for iterative methods for solving nonlinear ill-posed problems. In Surveys on Solution Methods for Inverse Problems. Springer, Vienna, Austria; 2000:7–34.
Magnanti TL, Perakis G: Solving variational inequality and fixed point problems by line searches and potential optimization. Mathematical Programming, Series A 2004,101(3):435–461. 10.1007/s10107-003-0476-5
Podilchuk CI, Mammone RJ: Image recovery by convex projections using a least-squares constraint. Journal of the Optical Society of America A 1990, 7: 517–521.
Sezan MI, Stark H: Applications of convex projection theory to image recovery in tomography and related areas. In Image Recovery: Theory and Application. Edited by: Stark H. Academic Press, Orlando, Fla, USA; 1987:415–462.
Tan K-K, Xu HK: Fixed point iteration processes for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1994,122(3):733–739. 10.1090/S0002-9939-1994-1203993-5
Yamada I, Ogura N: Adaptive projected subgradient method for asymptotic minimization of sequence of nonnegative convex functions. Numerical Functional Analysis and Optimization 2004,25(7–8):593–617.
Yamada I, Ogura N: Hybrid steepest descent method for variational inequality problem over the fixed point set of certain quasi-nonexpansive mappings. Numerical Functional Analysis and Optimization 2004,25(7–8):619–655.
Youla D: Mathematical theory of image restoration by the method of convex projections. In Image Recovery: Theory and Application. Edited by: Stark H. Academic Press, Orlando, Fla, USA; 1987:29–77.
Youla D: On deterministic convergence of iterations of related projection operators. Journal of Visual Communication and Image Representation 1990, 1: 12–20. 10.1016/1047-3203(90)90013-L
Ceng L-C, Ansari QH, Yao J-C: Mann-type steepest-descent and modified hybrid steepest-descent methods for variational inequalities in Banach spaces. Numerical Functional Analysis and Optimization 2008,29(9–10):987–1033. 10.1080/01630560802418391
Zeng L-C, Yao J-C: Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2006,10(5):1293–1303.
Ceng L-C, Yao J-C: Hybrid viscosity approximation schemes for equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Applied Mathematics and Computation 2008,198(2):729–741. 10.1016/j.amc.2007.09.011
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008,214(1):186–201. 10.1016/j.cam.2007.02.022
Ceng L-C, Schaible S, Yao J-C: Implicit iteration scheme with perturbed mapping for equilibrium problems and fixed point problems of finitely many nonexpansive mappings. Journal of Optimization Theory and Applications 2008,139(2):403–418. 10.1007/s10957-008-9361-y
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Ishikawa S: Fixed points and iteration of a nonexpansive mapping in a Banach space. Proceedings of the American Mathematical Society 1976,59(1):65–71. 10.1090/S0002-9939-1976-0412909-X
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1979,67(2):274–276. 10.1016/0022-247X(79)90024-6
Nevanlinna O, Reich S: Strong convergence of contraction semigroups and of iterative methods for accretive operators in Banach spaces. Israel Journal of Mathematics 1979,32(1):44–58. 10.1007/BF02761184
Combettes PL: On the numerical robustness of the parallel projection method in signal synthesis. IEEE Signal Processing Letters 2001,8(2):45–47. 10.1109/97.895371
Combettes PL: The convex feasibility problem in image recovery. In Advances in Imaging and Electron Physics. Volume 95. Edited by: Hawkes P. New York Academic, New York, NY, USA; 1996:155–270.
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1979, 67: 274–276. 10.1016/0022-247X(79)90024-6
Nevanlinna O, Reich S: Strong convergence of contraction semi-groups and of iterative methods for accretive operators in Banach spaces. Israel Journal of Mathematics 1979, 32: 44–58. 10.1007/BF02761184
Kim T-H, Xu H-K: Robustness of Mann's algorithm for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2007,327(2):1105–1115. 10.1016/j.jmaa.2006.05.009
García Falset J, Kaczor W, Kuczumow T, Reich S: Weak convergence theorems for asymptotically nonexpansive mappings and semigroups. Nonlinear Analysis: Theory, Methods & Applications 2001,43(3):377–401. 10.1016/S0362-546X(99)00200-X
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
van Dulst D: Equivalent norms and the fixed point property for nonexpansive mappings. The Journal of the London Mathematical Society. Second Series 1982,25(1):139–144. 10.1112/jlms/s2-25.1.139
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Browder FE: Convergence theorems for sequences of nonlinear operators in Banach spaces. Mathematische Zeitschrift 1967, 100: 201–225. 10.1007/BF01109805
Bruck RE: A simple proof of the mean ergodic theorem for nonlinear contractions in Banach spaces. Israel Journal of Mathematics 1979,32(2–3):107–116. 10.1007/BF02764907
Tan K-K, Xu HK: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. Journal of Mathematical Analysis and Applications 1993,178(2):301–308. 10.1006/jmaa.1993.1309
Marino G, Xu H-K: Convergence of generalized proximal point algorithms. Communications on Pure and Applied Analysis 2004,3(4):791–808.
Acknowledgments
This research was partially supported by Grant no. NSC 98-2923-E-110-003-MY3 and was also partially supported by the Leading Academic Discipline Project of Shanghai Normal University (DZL707), Innovation Program of Shanghai Municipal Education Commission Grant (09ZZ133), National Science Foundation of China (10771141), Ph.D. Program Foundation of Ministry of Education of China (20070270004), Science and Technology Commission of Shanghai Municipality Grant (075105118), and Shanghai Leading Academic Discipline Project (S30405).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ceng, L., Liou, Y. & Yao, J. Robustness of Mann Type Algorithm with Perturbed Mapping for Nonexpansive Mappings in Banach Spaces. Fixed Point Theory Appl 2010, 734181 (2010). https://doi.org/10.1155/2010/734181
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/734181
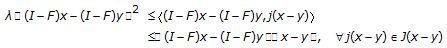
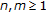 , define the mappings
, define the mappings  and
and 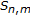 as follows:
as follows: