- Research Article
- Open access
- Published:
Common Fixed Points for Generalized 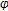 -Pair Mappings on Cone Metric Spaces
-Pair Mappings on Cone Metric Spaces
Fixed Point Theory and Applications volume 2010, Article number: 718340 (2010)
Abstract
We define the concept of generalized  -pair mappings and prove some common fixed point theorems for this type of mappings. Our results generalize some recent results.
-pair mappings and prove some common fixed point theorems for this type of mappings. Our results generalize some recent results.
1. Introduction
Huang and Zhang [1] recently introduced the concept of cone metric spaces and established some fixed point theorems for contractive mappings in these spaces. Afterwards, Rezapour and Hamlbarani [2] studied fixed point theorems of contractive type mappings by omitting the assumption of normality in cone metric spaces. Also, other authors proved the existence of points of coincidence, common fixed point, and coupled fixed point for mappings satisfying different contraction conditions in cone metric spaces (see [1–12]). In [6] Di Bari and Vetro introduced the concept of  -map and proved a main theorem generalizing some known results. We define the concept of generalized
-map and proved a main theorem generalizing some known results. We define the concept of generalized  -mappings and prove some results about common fixed points for such mappings. Our results generalize some results of Huang and Zhang [1], Di Bari and Vetro [6], and Abbas and Jungck [3]. First, we recall some standard notations and definitions in cone metric spaces.
-mappings and prove some results about common fixed points for such mappings. Our results generalize some results of Huang and Zhang [1], Di Bari and Vetro [6], and Abbas and Jungck [3]. First, we recall some standard notations and definitions in cone metric spaces.
Let  be a real Banach space and let
be a real Banach space and let  denote the zero element in
denote the zero element in  . A cone
. A cone  is a subset of
is a subset of  such that
such that
(i) is closed, nonempty, and
is closed, nonempty, and  ,
,
(ii)if  are nonnegative real numbers and
are nonnegative real numbers and  , then
, then  ,
,
(iii) .
.
For a given cone  , the partial ordering
, the partial ordering  with respect to
with respect to  is defined by
is defined by  if and only if
if and only if  . The notation
. The notation  will stand for
will stand for  but
but  . Also, we will use
. Also, we will use  to indicate that
to indicate that  where
where  denotes the interior of
denotes the interior of  . Using these notations, we have the following definition of a cone metric space.
. Using these notations, we have the following definition of a cone metric space.
Definition 1.1 (see [1]).
Let  be a nonempty set and let
be a nonempty set and let  be a real Banach space equipped with the partial ordering
be a real Banach space equipped with the partial ordering  with respect to the cone
with respect to the cone  . Suppose that the mapping
. Suppose that the mapping  satisfies the following conditions:
satisfies the following conditions:
 for all
for all  and
and  if and only if
if and only if  ,
,
 for all
for all  ,
,
 for all
for all  .
.
Then  is called a cone metric on
is called a cone metric on  , and
, and  is called a cone metric space.
is called a cone metric space.
The cone  is called normal if there exists a constant
is called normal if there exists a constant  such that for every
such that for every  if
if  then
then  . The least positive number satisfying this inequality is called the normal constant of
. The least positive number satisfying this inequality is called the normal constant of  . The cone
. The cone  is called regular if every increasing (decreasing) and bounded above (below) sequence is convergent in
is called regular if every increasing (decreasing) and bounded above (below) sequence is convergent in  . It is known that every regular cone is normal [1] (see also [2, Lemma
. It is known that every regular cone is normal [1] (see also [2, Lemma  ]).
]).
Definition 1.2 (see [1]).
Let  be a cone metric space, let
be a cone metric space, let  be a sequence in
be a sequence in  and let
and let  .
.
(i) is said to be Cauchy sequence if for every
is said to be Cauchy sequence if for every  with
with  there exists
there exists  such that for all
such that for all  ,
,  .
.
(ii) is said to be convergent to
is said to be convergent to  , denoted by
, denoted by  or
or  as
as  if for every
if for every  with
with  there exists
there exists  such that for all
such that for all  ,
,  .
.
(iii) is said to be complete if every Cauchy sequence in
is said to be complete if every Cauchy sequence in  is convergent in
is convergent in  .
.
(iv) is said to be sequentially compact if for every sequence
is said to be sequentially compact if for every sequence  in
in  there exists a subsequence
there exists a subsequence  of
of  such that
such that  is convergent in
is convergent in  .
.
Clearly, every sequentially compact cone metric space is complete (see [1–12]) for more related results about complete cone metric spaces). We also note that the relations  and
and 
 always hold true.
always hold true.
Definition 1.3 (see [13]).
Let  and
and  be self-mappings of a cone metric space
be self-mappings of a cone metric space  . One says that
. One says that  and
and  are compatible if
are compatible if  , whenever
, whenever  is a sequence in
is a sequence in  such that
such that  for some
for some  .
.
The concept of weakly compatible mappings is introduced as follows.
Definition 1.4 (see [13]).
The self-mappings  and
and  of a cone metric space
of a cone metric space  are said to be weakly compatible if they commute at their coincidence points, that is, if
are said to be weakly compatible if they commute at their coincidence points, that is, if  for some
for some  , then
, then  .
.
2. Main Results
In this section, we introduce the notation of generalized  -mapping and a contractive condition called generalized
-mapping and a contractive condition called generalized  -pair. We prove some results on common fixed points of these mappings on cone metric spaces.
-pair. We prove some results on common fixed points of these mappings on cone metric spaces.
Let  be a cone. A nondecreasing mapping
be a cone. A nondecreasing mapping  is called a
is called a  -mapping [6] if
-mapping [6] if
 and
and  for
for  ,
,
 for every
for every  ,
,
 for every
for every  .
.
Definition 2.1.
Let  be a cone and let
be a cone and let  be a sequence in
be a sequence in  . One says that
. One says that  if for every
if for every  with
with  there exists
there exists  such that
such that  for all
for all  .
.
For a nondecreasing mapping  we define the following conditions which will be used in the sequal:
we define the following conditions which will be used in the sequal:
 if and only if
if and only if  ,
,
for every  ,
,  if and only if
if and only if 
for every  ,
,  .
.
Definition 2.2.
The self-mappings  are called generalized
are called generalized  -pair if there exist a
-pair if there exist a  -mapping and a mapping
-mapping and a mapping  satisfying the conditions
satisfying the conditions  ,
,  and
and  such that
such that

for every  .
.
Now, we are in the position to state the following theorem.
Theorem 2.3.
Let  be a cone metric space and let
be a cone metric space and let  be a generalized
be a generalized  -pair. Suppose that
-pair. Suppose that  and
and  are weakly compatible with
are weakly compatible with  such that
such that  or
or  is complete. Then the self-mappings
is complete. Then the self-mappings  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Proof.
Let  and choose
and choose  such that
such that  . This can be done, since
. This can be done, since  . Continuing this process, after choosing
. Continuing this process, after choosing  , we choose
, we choose  such that
such that  . Since
. Since  and
and  are generalized
are generalized  -pair, by Definition 1.2, there exist a
-pair, by Definition 1.2, there exist a  -mapping and a mapping
-mapping and a mapping  satisfying the conditions
satisfying the conditions  and the inequality of (2.1). By (2.1), we deduce
and the inequality of (2.1). By (2.1), we deduce

Let  then, by
then, by  ,
,  . By
. By  ,
,

Therefore, one can find that  such that, for all
such that, for all  ,
,  . We show that
. We show that

for a fixed  and
and  . This holds when
. This holds when  . Now let (2.4) hold for some
. Now let (2.4) hold for some  , then we have
, then we have

Therefore, by induction and  we deduce that
we deduce that  is a Cauchy sequence. Suppose that
is a Cauchy sequence. Suppose that  is a complete subspace of
is a complete subspace of  , then there exists
, then there exists  such that
such that  and also
and also  (This holds also if
(This holds also if  is complete with
is complete with  ). Let
). Let  be such that
be such that  . We show that
. We show that  . By
. By  for
for  one can choose a natural number
one can choose a natural number  such that
such that  and
and  for all
for all  . Then,
. Then,

Thus,  for every
for every  . This implies that
. This implies that  and hence,
and hence,  . So applying
. So applying  we get
we get  which implies that
which implies that  , that is,
, that is,  is a point of coincidence of
is a point of coincidence of  and
and  . Now, we use the hypothesis that
. Now, we use the hypothesis that  and
and  are weakly compatible to deduce that
are weakly compatible to deduce that  is a common fixed point of
is a common fixed point of  and
and  . From
. From  , by compatibility of
, by compatibility of  and
and  , it follows that
, it follows that  . If
. If  , then we have
, then we have

which implies that  . So
. So  is a common fixed point of
is a common fixed point of  and
and  . The uniqueness of the common fixed point is clear.
. The uniqueness of the common fixed point is clear.
Example 2.4.
Let  and let
and let  be a normal cone. Let
be a normal cone. Let  with usual metric
with usual metric  . Define
. Define  by
by  and
and  , for all
, for all  . Also, define
. Also, define  by
by  and
and  , for all
, for all  . Then
. Then
(1) and
and  are weakly compatible,
are weakly compatible,
(2) ,
,
(3)we have  ,
,
(4) .
.
Example 2.5.
Let  and let
and let  be a normal cone. Let
be a normal cone. Let  with metric
with metric  . Define
. Define  by
by  and
and  , for all
, for all  . Also, define
. Also, define  by
by  and
and  , for all
, for all  . Then
. Then
(1) and
and  are weakly compatible,
are weakly compatible,
(2) ,
,
(3)we have  ,
,
(4) .
.
Example 2.6.
Let  and let
and let  be a normal cone. Let
be a normal cone. Let  with metric
with metric  . Define
. Define  by
by  and
and  , for all
, for all  . Also, define
. Also, define  by
by  and
and  , for all
, for all  . Then
. Then
(1) and
and  are weakly compatible,
are weakly compatible,
(2) ,
,
(3)we have  ,
,
(4) .
.
If we let the mapping  be the identity mapping in Theorem 2.3, then we obtain the following corollary.
be the identity mapping in Theorem 2.3, then we obtain the following corollary.
Corollary 2.7.
Let  be a cone metric space. Suppose that the mappings
be a cone metric space. Suppose that the mappings  satisfy
satisfy

for all  . If
. If  ,
,  and
and  are weakly compatible, and
are weakly compatible, and  or
or  is complete, then
is complete, then  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Remark 2.8.
Corollary 2.7 generalizes Theorem  in [6]. Also, if we choose the
in [6]. Also, if we choose the  -mapping defined by
-mapping defined by  , where
, where  is a constant, then Theorem 2.3 generalizes Theorem
is a constant, then Theorem 2.3 generalizes Theorem  in [3]. Furthermore, if we let
in [3]. Furthermore, if we let  be the identity map of
be the identity map of  , then we obtain Theorem
, then we obtain Theorem  in [1], that is, the extension of the Banach fixed point theorem for cone metric spaces.
in [1], that is, the extension of the Banach fixed point theorem for cone metric spaces.
If we replace the condition  with the following condition:
with the following condition:
there exists  such that
such that  for
for  and
and  , then we have the following theorems.
, then we have the following theorems.
Theorem 2.9.
Let  be a cone metric space and let
be a cone metric space and let  be self-mappings such that
be self-mappings such that

for all  where
where  is a nondecreasing mapping from
is a nondecreasing mapping from  into
into  satisfying the conditions
satisfying the conditions  ,
,  and
and  and
and  is a nondecreasing mapping satisfying the conditions
is a nondecreasing mapping satisfying the conditions  . Suppose that
. Suppose that  and
and  are weakly compatible,
are weakly compatible,  and
and  or
or  is complete. Then the mappings
is complete. Then the mappings  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Proof.
Let  be an arbitrary point in
be an arbitrary point in  . Choose a point
. Choose a point  such that
such that  . This can be done since
. This can be done since  . Continuing this process, after choosing
. Continuing this process, after choosing  with
with  , by (2.9) and
, by (2.9) and  we have
we have

Consequently,

where  . For
. For  we have
we have

Then  as
as  and hence, by
and hence, by  ,
,  is a Cauchy sequence. Suppose that
is a Cauchy sequence. Suppose that  is a complete subspace of
is a complete subspace of  , then there exists
, then there exists  such that
such that  and also
and also  (this holds if
(this holds if  is complete). Let
is complete). Let  be such that
be such that  . By
. By  , for a fixed
, for a fixed  and every
and every  there exists a natural number
there exists a natural number  such that
such that  and
and  for all
for all  . Hence,
. Hence,

which implies that

Thus,  for all
for all  . This implies that
. This implies that  and therefore,
and therefore,  . Since
. Since  and
and  are weakly compatible,
are weakly compatible,  . If
. If  , then
, then

which gives  and hence,
and hence,  . So
. So  is a common fixed point for
is a common fixed point for  and
and  . The uniqueness of common fixed point is clear.
. The uniqueness of common fixed point is clear.
If in Theorem 2.9 we let  be
be  and let the
and let the  -mapping be
-mapping be  , where
, where  is a constant, then we obtain the following corollary.
is a constant, then we obtain the following corollary.
Corollary 2.10.
Let  be a cone metric space and let
be a cone metric space and let  be self-mappings such that
be self-mappings such that

for all  , where
, where  is a constant. Suppose that
is a constant. Suppose that  and
and  are weakly compatible, the range of
are weakly compatible, the range of  contains the range of
contains the range of  and
and  or
or  is complete. Then the mappings
is complete. Then the mappings  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Remark 2.11.
Corollary 2.10 generalizes Theorem  of [3]. If in Corollary 2.10 we let
of [3]. If in Corollary 2.10 we let  be the identity map on
be the identity map on  , then we obtain Theorem
, then we obtain Theorem  of [1].
of [1].
Theorem 2.12.
Let  be a cone metric space and let
be a cone metric space and let  be self-mappings such that
be self-mappings such that

for all  . Suppose that
. Suppose that  and
and  are weakly compatible, the range of
are weakly compatible, the range of  contains the range of
contains the range of  and
and  or
or  is complete. Then the mappings
is complete. Then the mappings  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Proof.
Let  be an arbitrary point in
be an arbitrary point in  . Choose a point
. Choose a point  in
in  such that
such that  . This can be done since
. This can be done since  . Continuing this process having chosen
. Continuing this process having chosen  in
in  such that
such that  , we have
, we have

So,

where  . Now let
. Now let  with
with  . Then,
. Then,

Following an argument similar to that one given in Theorem 2.9, we obtain a unique common fixed point of  and
and  .
.
If in Theorem 2.12 we let  be the identity map on
be the identity map on  and let the
and let the  -map be
-map be  , where
, where  is a constant, then we obtain the following corollary.
is a constant, then we obtain the following corollary.
Corollary 2.13.
Let  be a cone metric space and let
be a cone metric space and let  be self-mappings such that
be self-mappings such that

for all  , where
, where  is a constant. Suppose that
is a constant. Suppose that  and
and  are weakly compatible, the range of
are weakly compatible, the range of  contains the range of
contains the range of  and
and  or
or  is complete. Then the mappings
is complete. Then the mappings  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Remark 2.14.
Corollary 2.13 generalizes Theorem  of [3] and if in Corollary 2.13 we let
of [3] and if in Corollary 2.13 we let  be the identity map on
be the identity map on  , then we obtain Theorem
, then we obtain Theorem  of [1].
of [1].
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Rezapour S, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. Journal of Mathematical Analysis and Applications 2008,341(1):416–420. 10.1016/j.jmaa.2007.09.070
Arshad M, Azam A, Vetro P: Some common fixed point results in cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-11.
Azam A, Arshad M, Beg I: Common fixed point theorems in cone metric spaces. Journal of Nonlinear Science and Its Applications 2009,2(4):204–213.
Di Bari C, Vetro P: -pairs and common fixed points in cone metric spaces. Rendiconti del Circolo Matematico di Palermo 2008,57(2):279–285. 10.1007/s12215-008-0020-9
Ilić D, Rakočević V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Ilić D, Rakočević V: Quasi-contraction on a cone metric space. Applied Mathematics Letters 2009,22(5):728–731. 10.1016/j.aml.2008.08.011
Jungck G, Radenović S, Radojević S, Rakočević V: Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-13.
Jleli M, Samet B: The Kannan's fixed point theorem in a cone rectangular metric space. Journal of Nonlinear Science and Its Applications 2009,2(3):161–167.
Sabetghadam F, Masiha HP, Sanatpour A: Some coupled fixed point theorems in cone metric spaces. Fixed Point Theory and Application 2009, 2009:-8.
Vetro P: Common fixed points in cone metric spaces. Rendiconti del Circolo Matematico di Palermo 2007,56(3):464–468. 10.1007/BF03032097
Jungck G: Compatible mappings and common fixed points. International Journal of Mathematics and Mathematical Sciences 1986,9(4):771–779. 10.1155/S0161171286000935
Acknowledgment
The authors would like to thank the referees for their valuable and useful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sabetghadam, F., Masiha, H. Common Fixed Points for Generalized 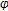 -Pair Mappings on Cone Metric Spaces.
Fixed Point Theory Appl 2010, 718340 (2010). https://doi.org/10.1155/2010/718340
-Pair Mappings on Cone Metric Spaces.
Fixed Point Theory Appl 2010, 718340 (2010). https://doi.org/10.1155/2010/718340
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/718340