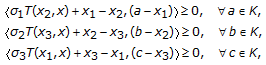- Research Article
- Open access
- Published:
A Hybrid Proximal Point Three-Step Algorithm for Nonlinear Set-Valued Quasi-Variational Inclusions System Involving 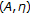 -Accretive Mappings
-Accretive Mappings
Fixed Point Theory and Applications volume 2010, Article number: 635382 (2010)
Abstract
The main purpose of this paper is to introduce and study a new class of generalized nonlinear set-valued quasi-variational inclusions system involving  -accretive mappings in Banach spaces. By using the resolvent operator due to Lan-Cho-Verma associated with
-accretive mappings in Banach spaces. By using the resolvent operator due to Lan-Cho-Verma associated with  -accretive mappings and the matrix analysis method, we prove the convergence of a new hybrid proximal point three-step iterative algorithm for this system of set-valued variational inclusions and an existence theorem of solutions for this kind of the variational inclusions system. The results presented in this paper generalize, improve, and unify some recent results in this field.
-accretive mappings and the matrix analysis method, we prove the convergence of a new hybrid proximal point three-step iterative algorithm for this system of set-valued variational inclusions and an existence theorem of solutions for this kind of the variational inclusions system. The results presented in this paper generalize, improve, and unify some recent results in this field.
1. Introduction
The variational inclusion, which was introduced and studied by Hassouni and Moudafi [1], is a useful and important extension of the variational inequality. It provides us with a unified, natural, novel, innovative, and general technique to study a wide class of problems arising in different branches of mathematical and engineering sciences. Various variational inclusions have been intensively studied in recent years. Ding and Luo [2], Verma [3, 4], Huang [5], Fang et al. [6], Fang and Huang [7], Fang et al. [8], Lan et al. [9], Zhang et al. [10] introduced the concepts of  -subdifferential operators, maximal
-subdifferential operators, maximal  -monotone operators,
-monotone operators,  -monotone operators,
-monotone operators,  -monotone operators,
-monotone operators,  -monotone operators,
-monotone operators,  -accretive mappings,
-accretive mappings,  -monotone operators, and defined resolvent operators associated with them, respectively. Moreover, by using the resolvent operator technique, many authors constructed some approximation algorithms for some nonlinear variational inclusions in Hilbert spaces or Banach spaces. Verma has developed a hybrid version of the Eckstein-Bertsekas [11] proximal point algorithm, introduced the algorithm based on the
-monotone operators, and defined resolvent operators associated with them, respectively. Moreover, by using the resolvent operator technique, many authors constructed some approximation algorithms for some nonlinear variational inclusions in Hilbert spaces or Banach spaces. Verma has developed a hybrid version of the Eckstein-Bertsekas [11] proximal point algorithm, introduced the algorithm based on the  -maximal monotonicity framework [12], and studied convergence of the algorithm. For the past few years, many existence results and iterative algorithms for various variational inequalities and variational inclusion problems have been studied. For details, please see [1–37] and the references therein.
-maximal monotonicity framework [12], and studied convergence of the algorithm. For the past few years, many existence results and iterative algorithms for various variational inequalities and variational inclusion problems have been studied. For details, please see [1–37] and the references therein.
On the other hand, some new and interesting problems for systems of variational inequalities were introduced and studied. Peng and Zhu [14], Cohen and Chaplais [15], Bianchi [16], and Ansari and Yao [17] considered a system of scalar variational inequalities. Ansari et al. [18] introduced and studied a system of vector equilibrium problems and a system of vector variational inequalities using a fixed point theorem. Allevi et al. [19] considered a system of generalized vector variational inequalities and established some existence results with relative pseudomonotonicity. Kassay and Kolumbán [20] introduced a system of variational inequalities and proved an existence theorem through the Ky Fan lemma. Kassay et al. [21] studied Minty and Stampacchia variational inequality systems with the help of the Kakutani-Fan-Glicksberg fixed point theorem. J. K. Kim and D. S. Kim [22] introduced a new system of generalized nonlinear quasi-variational inequalities and obtained some existence and uniqueness results on solutions for this system of generalized nonlinear quasi-variational inequalities in Hilbert spaces. Cho et al. [23] introduced and studied a new system of nonlinear variational inequalities in Hilbert spaces. They proved some existence and uniqueness theorems for solutions for the system of nonlinear variational inequalities. As generalizations of a system of variational inequalities, Agarwal et al. [24] introduced a system of generalized nonlinear mixed quasi-variational inclusions and investigated the sensitivity analysis of solutions for this system of generalized nonlinear mixed quasi-variational inclusions in Hilbert spaces. Kazmi and Bhat [25] introduced a system of nonlinear variational-like inclusions and gave an iterative algorithm for finding its approximate solution. Fang and Huang [26], Fang et al. [8] introduced and studied a new system of variational inclusions involving H-monotone operators and  -monotone operators, respectively. Yan et al. [27] introduced and studied a system of set-valued variational inclusions which is more general than the model in [3].
-monotone operators, respectively. Yan et al. [27] introduced and studied a system of set-valued variational inclusions which is more general than the model in [3].
Inspired and motivated by recent research work in this field, in this paper, a general set-valued quasi-variational inclusions system with  -accretive mappings is studied in Banach spaces, which includes many variational inclusions (inequalities) as special cases. By using the resolvent operator associated with
-accretive mappings is studied in Banach spaces, which includes many variational inclusions (inequalities) as special cases. By using the resolvent operator associated with  -accretive operator due to Lan, an existence theorem of solution for this class of variational inclusions is proved, and a new hybrid proximal point algorithm is established and suggested, and the convergence of iterative sequences generated by the algorithm is discussed in
-accretive operator due to Lan, an existence theorem of solution for this class of variational inclusions is proved, and a new hybrid proximal point algorithm is established and suggested, and the convergence of iterative sequences generated by the algorithm is discussed in  -uniformly smooth Banach spaces. The results presented in this paper generalize, and unify some recent results in this field.
-uniformly smooth Banach spaces. The results presented in this paper generalize, and unify some recent results in this field.
2. Preliminaries
Let  be a real Banach space with dual space
be a real Banach space with dual space  ,
,  be the dual pair between
be the dual pair between  and
and  ,
,  denote the family of all the nonempty subsets of
denote the family of all the nonempty subsets of  , and
, and  denote the family of all nonempty closed bounded subsets of
denote the family of all nonempty closed bounded subsets of  . The generalized duality mapping
. The generalized duality mapping  is defined by
is defined by

where  is a constant.
is a constant.
The modulus of smoothness of  is the function
is the function  defined by
defined by

A Banach space  is called uniformly smooth if
is called uniformly smooth if

 is called
is called  -uniformly smooth if there exists a constant
-uniformly smooth if there exists a constant  such that
such that

Remark 2.1.
In particular,  is the usual normalized duality mapping. It is known that,
is the usual normalized duality mapping. It is known that,  for all
for all  ,
,  is single-valued if
is single-valued if  is strictly convex [10], or
is strictly convex [10], or  is uniformly smooth (Hilbert space and
is uniformly smooth (Hilbert space and  space are
space are  uniformly Banach space), and if
uniformly Banach space), and if  , the Hilbert space, then
, the Hilbert space, then  becomes the identity mapping on
becomes the identity mapping on  . In what follows we always denote the single-valued generalized duality mapping by
. In what follows we always denote the single-valued generalized duality mapping by  in real uniformly smooth Banach space
in real uniformly smooth Banach space  unless otherwise states.
unless otherwise states.
Let us recall the following results and concepts.
Definition 2.2.
A single-valued mapping  is said to be
is said to be  -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

Definition 2.3.
A single-valued mapping  is said to be
is said to be
(i)accretive if

(ii)strictly accretive if  is accretive and
is accretive and  if and only if
if and only if  for all
for all  ;
;
(iii) -strongly
-strongly  -accretive if there exists a constant
-accretive if there exists a constant  such that
such that

(iv) -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

Definition 2.4.
A set-valued mapping  is said to be
is said to be
(i) -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

where  is the Hausdorff metric on
is the Hausdorff metric on 
(ii) -strongly
-strongly  -accretive
-accretive if there exists a constant
if there exists a constant  such that
such that

(iii) -relaxed cocoercive if there exist two constants
-relaxed cocoercive if there exist two constants  such that
such that

(iv) -strongly
-strongly  -accretive with respect to the first argument of the mapping
-accretive with respect to the first argument of the mapping  , if there exists a constant
, if there exists a constant  such that
such that

where  .
.
Definition 2.5.
Let  be a single-valued mapping and
be a single-valued mapping and  be a set-valued mapping
be a set-valued mapping  . For
. For  , a single-valued mapping
, a single-valued mapping  is said to be
is said to be
(i) -Lipschitz continuous if there exist three constants
-Lipschitz continuous if there exist three constants  such that
such that

(ii) -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first argument, if there exist constants
in the first argument, if there exist constants  such that
such that

In a similar way, we can define Lipschitz continuity and  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  of
of  in the second, or the three argument.
in the second, or the three argument.
Definition 2.6.
Let  and
and  be single-valued mappings. A set-valued mapping
be single-valued mappings. A set-valued mapping  is said to be
is said to be
-
(i)
accretive if
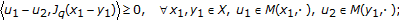 (215)
(215)
(ii) -accretive if
-accretive if

(iii) -relaxed
-relaxed  -accretive, if there exists a constant
-accretive, if there exists a constant  such that
such that

(iv) -accretive if
-accretive if  is accretive and
is accretive and  for all
for all  ;
;
(v) -accretive if
-accretive if  is
is  -relaxed
-relaxed  -accretive and
-accretive and  for every
for every  .
.
Based on [9], we can define the resolvent operator  as follows.
as follows.
Definition 2.7 (see [9]).
Let  be a single-valued mapping
be a single-valued mapping  be a strictly
be a strictly  -accretive single-valued mapping and
-accretive single-valued mapping and  be a (
be a ( )-accretive mapping. The resolvent operator
)-accretive mapping. The resolvent operator  is defined by
is defined by

where  is a constant.
is a constant.
Remark 2.8.
The  -accretive mappings are more general than
-accretive mappings are more general than  -monotone mappings,
-monotone mappings,  -accretive mappings,
-accretive mappings,  -monotone operators,
-monotone operators,  -subdifferential operators, and
-subdifferential operators, and  -accretive mappings in Banach space or Hilbert space, and the resolvent operators associated with
-accretive mappings in Banach space or Hilbert space, and the resolvent operators associated with  -accretive mappings include as special cases the corresponding resolvent operators associated with
-accretive mappings include as special cases the corresponding resolvent operators associated with  -monotone operators,
-monotone operators,  -accretive mappings,
-accretive mappings,  -accretive mappings,
-accretive mappings,  -monotone operators,
-monotone operators,  -subdifferential operators [5, 6, 11, 14, 15, 26, 27, 35–37].
-subdifferential operators [5, 6, 11, 14, 15, 26, 27, 35–37].
Lemma 2.9 (see [9]).
Let  be
be  -Lipschtiz continuous mapping,
-Lipschtiz continuous mapping,  be an
be an  -strongly
-strongly  -accretive mapping, and
-accretive mapping, and  be set-valued
be set-valued  -accretive mapping, respectively. Then the generalized resolvent operator
-accretive mapping, respectively. Then the generalized resolvent operator  is
is  -Lipschitz continuous, that is,
-Lipschitz continuous, that is,

where  ,
,  , and
, and  .
.
In the study of characteristic inequalities in  -uniformly smooth Banach spaces
-uniformly smooth Banach spaces  , Xu [29] proved the following result.
, Xu [29] proved the following result.
Lemma 2.10 (see [29]).
Let  be a real uniformly smooth Banach space. Then
be a real uniformly smooth Banach space. Then  is
is  -uniformly smooth if andonly if there exists a constant
-uniformly smooth if andonly if there exists a constant  such that for all
such that for all 

Theorem 2.11.
Let the function  where
where  and
and  , then
, then

Proof.
Let  , where
, where  ,
,  ,
,  ,
,  . Then
. Then  by the
by the  . We can obtain
. We can obtain

Let  , and
, and  , where
, where  . It follows that
. It follows that

This completes the proof.
Corollary 2.12.
Let  be real, for any real
be real, for any real  , if
, if  , then
, then

Proof.
The proof directly follows from the (i) in the Theorem 2.11.
Definition 2.13 (see [38]).
Let  is a real
is a real be a real matrix set, then the mappings
be a real matrix set, then the mappings

is called the  -norm, and
-norm, and  -norm, respectively.
-norm, respectively.
Obviously,  may be a Banach space on real field
may be a Banach space on real field  , which is called the real matrix-Banach space.
, which is called the real matrix-Banach space.
Definition 2.14 (see [38]).
Let  is a real
is a real be a real matrix-Banach Space with the matrix-norm
be a real matrix-Banach Space with the matrix-norm  (
( , or
, or  ). If
). If

then the matrix  is called the limit matrix of matrix sequence
is called the limit matrix of matrix sequence  , noted by
, noted by  , where
, where  is a real sequence,
is a real sequence,  ,
,  and
and  ,
,  .
.
Lemma 2.15 (see [38]).
 , if and only if
, if and only if

Hence, if  , then
, then 
In this paper, the matrix norm symbol  is noted by
is noted by  .
.
Definition 2.16.
Let  be real numbers, and
be real numbers, and  and
and  be two real vectors, then
be two real vectors, then  if and only if
if and only if  .
.
3. Quasi-Variational Inclusions System Problem and Hybrid Proximal Point Algorithm
Let  be a real
be a real  -uniformly smooth Banach space with dual space
-uniformly smooth Banach space with dual space  ,
,  be the dual pair between
be the dual pair between  and
and  ,
,  denote the family of all the nonempty subsets of
denote the family of all the nonempty subsets of  , and
, and  denote the family of all nonempty closed bounded subsets of
denote the family of all nonempty closed bounded subsets of  . The generalized duality mapping
. The generalized duality mapping  is defined by
is defined by

where  is a constant. Now, we consider the following generational nonlinear set-valued quasi-variational inclusions system problem with
is a constant. Now, we consider the following generational nonlinear set-valued quasi-variational inclusions system problem with  -accretive mappings (GNSVQVIS) problem.
-accretive mappings (GNSVQVIS) problem.
Let  ,
,  , and
, and  be single-valued mappings for
be single-valued mappings for  . Let
. Let  be a set-valued
be a set-valued  -accretive mapping and
-accretive mapping and  be set-valued mappings for
be set-valued mappings for  .
.
For any  , finding
, finding  such that
such that  ,
,  ,
,  ,
,  ,
,  , and
, and

where 
Remark 3.1.
Some special cases of problem (3.2) are as follows.
-
(i)
If
 ,
, 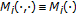 ,
, 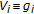 ,
,  ,
,  and
and 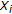 is a Hilbert space, then the problem (3.2) reduces to the problem associated with the system of variational inclusions with
is a Hilbert space, then the problem (3.2) reduces to the problem associated with the system of variational inclusions with 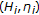 -monotone operators, which is finding
-monotone operators, which is finding  such that
such that  ,
, 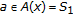 ,
, 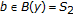 ,
, 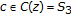 ,
,  ,
,  ,
, 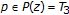 ,
,  ,
, 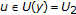 ,
, 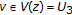 and
and 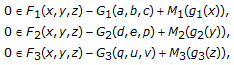 (33)
(33)
where 
Problem (3.3) contains the system of variational inclusions with  -monotone operators in Peng and Zhu [14], and the system of variational inclusions with
-monotone operators in Peng and Zhu [14], and the system of variational inclusions with  -monotone operators in [8] as special cases.
-monotone operators in [8] as special cases.
-
(ii)
If
 ,
, 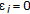 ,
,  (Hilbert space) and,
(Hilbert space) and, 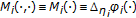 , where
, where  is a proper,
is a proper,  -subdifferentiable functional and
-subdifferentiable functional and 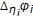 denotes the
denotes the 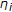 -subdifferential operator of
-subdifferential operator of 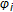 , then problem(3.3) changes to the problem associated with the following system of variational-like inequalities, which is finding
, then problem(3.3) changes to the problem associated with the following system of variational-like inequalities, which is finding 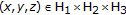 such that
such that 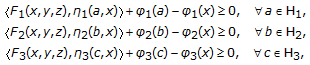 (34)
(34)
where 
-
(iii)
If
 ,
,  ,
, 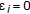 ,
, 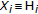 (Hilbert space) and
(Hilbert space) and 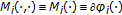 , where
, where 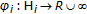 is a proper, convex, lower semicontinuous functional and
is a proper, convex, lower semicontinuous functional and  denotes the subdifferential operator of
denotes the subdifferential operator of 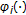 , then problem (3.3) changes to the problem associated with the following system of variational inequalities, which is finding
, then problem (3.3) changes to the problem associated with the following system of variational inequalities, which is finding 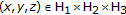 such that
such that 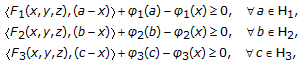 (35)
(35)
where 
-
(iv)
If
 ,
, 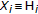 (Hilbert space), and
(Hilbert space), and 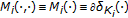 , where
, where 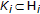 is a nonempty, closed, and convex subsets and
is a nonempty, closed, and convex subsets and 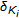 denotes the indicator of
denotes the indicator of  , then problem (3.5) reduces to the problem associated with the following system of variational inequalities, which is finding
, then problem (3.5) reduces to the problem associated with the following system of variational inequalities, which is finding  such that
such that 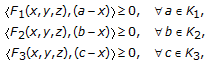 (36)
(36)
where 
-
(v)
If
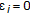 , and
, and 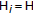 is a Hilbert space,
is a Hilbert space, 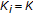 is a nonempty, closed and convex subset, for all
is a nonempty, closed and convex subset, for all 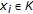 ,
,  , where
, where 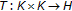 is a mapping on
is a mapping on 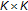 ,
, 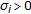 is a constant, then problem (3.6) changes to the following problem: find
is a constant, then problem (3.6) changes to the following problem: find  such that
such that 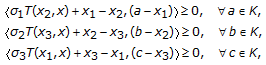 (37)
(37)
where 
Moreover, if  , problem (3.7) becomes the problem introduced and studied by Verma [31].
, problem (3.7) becomes the problem introduced and studied by Verma [31].
We can see that problem (3.2) includes a number of known classes of system of variational inequalities and variational inclusions as special cases (see, e.g., [2–9, 11–27, 29, 32–37]). It is worth noting that problems (3.2)–(3.7) are all new mathematical models.
Theorem 3.2.
Let  be a Banach space,
be a Banach space,  be
be  -Lipschtiz continuous mapping,
-Lipschtiz continuous mapping,  be an
be an  -strongly
-strongly  -accretive mapping, and
-accretive mapping, and  be a set-valued
be a set-valued  -accretive mapping for
-accretive mapping for  . Then the following statements are mutually equivalent.
. Then the following statements are mutually equivalent.
(i)An element  is a solution of problem (3.2),
is a solution of problem (3.2),  .
.
(ii)For  and
and  ,
,  ,
,  ,
,  , the following relations hold:
, the following relations hold:

where  is a constant and
is a constant and  , respectively.
, respectively.
Proof.
This directly follows from definition of  and the problem (3.2) for
and the problem (3.2) for  .
.
Algorithm 3.3.
Let  ,
, and
and  be three nonnegative sequences such that
be three nonnegative sequences such that

Step 1.
For arbitrarily chosen initial points  ,
,  ,
,  ,
,  ,
,  ,
,  , Set
, Set

where the  satisfies
satisfies

By using [39], we can choose suitable  ,
,  ,
,  and
and  such that
such that

for  .
.
Step 2.
The sequences  , and
, and  are generated by an iterative procedure:
are generated by an iterative procedure:


where

Thus, we can choose suitable  ,
,  ,
,  and
and  such that
such that

for  and
and  .
.
Remark 3.4.
If we choose suitable some operators  , and space
, and space  , then Algorithm 3.3 can be degenerated to a number of known algorithms for solving the system of variational inequalities and variational inclusions (see, e.g., [2–9, 11–27, 29, 31–35, 38, 39]).
, then Algorithm 3.3 can be degenerated to a number of known algorithms for solving the system of variational inequalities and variational inclusions (see, e.g., [2–9, 11–27, 29, 31–35, 38, 39]).
4. Existence and Convergence
In this section, we prove the existence of solutions for problem (3.2) and the convergence of iterative sequences generated by Algorithm 3.3.
Theorem 4.1.
Let  be a
be a  -uniformly smooth Banach space,
-uniformly smooth Banach space,  be a
be a  -Lipschtiz continuous mapping, and
-Lipschtiz continuous mapping, and  be a
be a  -strongly
-strongly  -accretive mapping and
-accretive mapping and  -Lipschitz continuous. Let
-Lipschitz continuous. Let  be a set-valued mappings of
be a set-valued mappings of  -Lipschitz continuous with constants
-Lipschitz continuous with constants  , and
, and  be
be  -relaxed cocoercive, respectively. Let
-relaxed cocoercive, respectively. Let  be Lipschitz continuous with constants
be Lipschitz continuous with constants  and
and  for all
for all  , and
, and  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first, second and third arguments, respectively. Let
in the first, second and third arguments, respectively. Let  be Lipschitz continuous with constants
be Lipschitz continuous with constants  and
and  for all
for all  . Let
. Let  ,
,  ,
,  be some set-valued mappings such that for each given
be some set-valued mappings such that for each given  ,
,  ,
,  ,
,  and
and  be an
be an  -accretive mapping, respectively. Suppose that
-accretive mapping, respectively. Suppose that  ,
,  and
and  are three nonnegative sequences with
are three nonnegative sequences with


where  is the same as in Lemma 2.10,
is the same as in Lemma 2.10,  , and
, and  . Then the problem (3.2) has a solution
. Then the problem (3.2) has a solution  .
.
Proof.
Let

for  . Then it follows from (3.13) that
. Then it follows from (3.13) that

Since  is
is  -Lipschitz continuous with constants
-Lipschitz continuous with constants  and
and  -relaxed cocoercive,
-relaxed cocoercive,

By (3.15), we have

Since  and
and  , by Lemma 2.9, we have
, by Lemma 2.9, we have

Since  is Lipschitz continuous with constants
is Lipschitz continuous with constants  , and
, and  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first arguments,
in the first arguments,  be Lipschitz continuous with constants
be Lipschitz continuous with constants  , respectively, Lemma 2.10, we have
, respectively, Lemma 2.10, we have

By (3.13), we know that  . Since
. Since  is Lipschitz continuous with constants
is Lipschitz continuous with constants  , and
, and  is
is  -Lipschitz continuous with constants
-Lipschitz continuous with constants  , respectively, combing (4.4)–(4.8) and using Corollary 2.12, we have
, respectively, combing (4.4)–(4.8) and using Corollary 2.12, we have

and so

For the sequences  , we have
, we have

Since  is
is  -Lipschitz continuous with constant
-Lipschitz continuous with constant  and
and  -relaxed cocoercive, we have
-relaxed cocoercive, we have

It follows from (3.15) that

Since  and
and  , by using Lemma 2.9, we obtain
, by using Lemma 2.9, we obtain

Since  is Lipschitz continuous with constants
is Lipschitz continuous with constants  , and
, and  -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first arguments,
in the first arguments,  is Lipschitz continuous with constants
is Lipschitz continuous with constants  , respectively, it follows from Lemma 2.10 that
, respectively, it follows from Lemma 2.10 that

By (3.13), we know that  . Since
. Since  is Lipschitz continuous with constants
is Lipschitz continuous with constants  , and
, and  is
is  -Lipschitz continuous with constants
-Lipschitz continuous with constants  , respectively, combing (4.11)–(4.20) and using Corollary 2.12, we have
, respectively, combing (4.11)–(4.20) and using Corollary 2.12, we have

and so

Using the same as the method, we can obtain

Let

Letting  , then combining (4.10),(4.17)–(4.19), we have
, then combining (4.10),(4.17)–(4.19), we have  , where
, where

which is called the iterative matrix for Hybrid proximal point three-step algorithm of nonlinear set-valued quasi-variational inclusions system involving  -Accretive mappings. Using (4.20),
-Accretive mappings. Using (4.20),  ,
,  ,
,  , we have
, we have

where  , and
, and

By using [38], we have

Letting

It follows from (4.22) and assumption condition (4.2) that  and hence there exists
and hence there exists  and
and  such that
such that  for all
for all  . Therefore, by (4.23), we have
. Therefore, by (4.23), we have

Without loss of generality we assume

By the property of the matrix norm [38], for  , we have
, we have

Hence, for any  and
and  , we have
, we have

It follows that  , as
, as  , and so that the
, and so that the  is a Cauchy sequence in
is a Cauchy sequence in  . Let
. Let  as
as  . By the Lipschitz continuity of
. By the Lipschitz continuity of  , we can obtain
, we can obtain

It follows that  ,
,  ,
,  , and
, and  are also Cauchy sequences in
are also Cauchy sequences in  . We can assume that
. We can assume that  ,
,  ,
,  , and
, and  , respectively. Noting that
, respectively. Noting that  , we have
, we have

Hence  and therefore
and therefore  . Similarly, we can prove that
. Similarly, we can prove that  ,
,  , and
, and  . By the Lipschitz continuity of
. By the Lipschitz continuity of  ,
,  ,
,  , and
, and  , we have
, we have

for  , where
, where  is a constant. Thus, by Theorem (3.3), we know that
is a constant. Thus, by Theorem (3.3), we know that  is solution of problem (3.2). This completes the proof.
is solution of problem (3.2). This completes the proof.
Corollary 4.2.
Let  be a
be a  -uniformly smooth Banach space,
-uniformly smooth Banach space,  be a
be a  -Lipschtiz continuous mapping, and
-Lipschtiz continuous mapping, and  be an
be an  -strongly
-strongly  -accretive mapping and
-accretive mapping and  -Lipschitz continuous. Let
-Lipschitz continuous. Let  be the same as in Theorem 4.1. If
be the same as in Theorem 4.1. If

where  is the same as in Lemma 2.10,
is the same as in Lemma 2.10,  , and
, and  . Then problem (3.2) has a solution
. Then problem (3.2) has a solution  .
.
Remark 4.3.
For a suitable choice of the mappings  , we can obtain several known results in [2–5, 9, 11–27, 29, 32–37] as special cases of Theorem 4.1 and Corollary 4.2.
, we can obtain several known results in [2–5, 9, 11–27, 29, 32–37] as special cases of Theorem 4.1 and Corollary 4.2.
References
Hassouni A, Moudafi A: A perturbed algorithm for variational inclusions. Journal of Mathematical Analysis and Applications 1994,185(3):706–712. 10.1006/jmaa.1994.1277
Ding XP, Luo CL: Perturbed proximal point algorithms for general quasi-variational-like inclusions. Journal of Computational and Applied Mathematics 2000,113(1–2):153–165. 10.1016/S0377-0427(99)00250-2
Verma RU: -monotonicity and applications to nonlinear variational inclusion problems. Journal of Applied Mathematics and Stochastic Analysis 2004, (2):193–195.
Verma RU: Projection methods, algorithms, and a new system of nonlinear variational inequalities. Computers & Mathematics with Applications 2001,41(7–8):1025–1031. 10.1016/S0898-1221(00)00336-9
Huang N-J: Nonlinear implicit quasi-variational inclusions involving generalized -accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425.
Fang YP, Cho YJ, Kin JK: -accretive operators and approximating solutions for systems of variational inclusions in Banach spaces. to appear in Applied Mathematics Letters
Fang Y-P, Huang N-J: -accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7
Fang Y-P, Huang N-J, Thompson HB: A new system of variational inclusions with -monotone operators in Hilbert spaces. Computers & Mathematics with Applications 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037
Lan H-Y, Cho YJ, Verma RU: Nonlinear relaxed cocoercive variational inclusions involving -accretive mappings in Banach spaces. Computers & Mathematics with Applications 2006,51(9–10):1529–1538. 10.1016/j.camwa.2005.11.036
Zhang Q-B, Ding X-P, Cheng C-Z: Resolvent operator technique for generalized implicit variational-like inclusion in Banach space. Journal of Mathematical Analysis and Applications 2010,361(2):283–292. 10.1016/j.jmaa.2006.01.090
Eckstein J, Bertsekas DP: On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming 1992,55(1–3):293–318.
Verma RU: A hybrid proximal point algorithm based on the -maximal monotonicity framework. Applied Mathematics Letters 2008,21(2):142–147. 10.1016/j.aml.2007.02.017
Shim SH, Kang SM, Huang NJ, Cho YJ: Perturbed iterative algorithms with errors for completely generalized strongly nonlinear implicit quasivariational inclusions. Journal of Inequalities and Applications 2000,5(4):381–395. 10.1155/S1025583400000205
Peng J-W, Zhu D-L: Three-step iterative algorithm for a system of set-valued variational inclusions with -monotone operators. Nonlinear Analysis: Theory, Methods & Applications 2008,68(1):139–153. 10.1016/j.na.2006.10.037
Cohen G, Chaplais F: Nested monotony for variational inequalities over product of spaces and convergence of iterative algorithms. Journal of Optimization Theory and Applications 1988,59(3):369–390. 10.1007/BF00940305
Bianchi M: Pseudo P-monotone operators and variational inequalities. Istituto di Econometria e Matematica per le Decisioni Economiche, Universita Cattolica del Sacro Cuore, Milan, Italy; 1993.
Ansari QH, Yao J-C: A fixed point theorem and its applications to a system of variational inequalities. Bulletin of the Australian Mathematical Society 1999,59(3):433–442. 10.1017/S0004972700033116
Ansari QH, Schaible S, Yao JC: System of vector equilibrium problems and its applications. Journal of Optimization Theory and Applications 2000,107(3):547–557. 10.1023/A:1026495115191
Allevi E, Gnudi A, Konnov IV: Generalized vector variational inequalities over product sets. Nonlinear Analysis: Theory, Methods & Applications 2001,47(1):573–582. 10.1016/S0362-546X(01)00202-4
Kassay G, Kolumbán J: System of multi-valued variational inequalities. Publicationes Mathematicae Debrecen 2000,56(1–2):185–195.
Kassay G, Kolumbán J, Páles Z: Factorization of Minty and Stampacchia variational inequality systems. European Journal of Operational Research 2002,143(2):377–389. 10.1016/S0377-2217(02)00290-4
Kim JK, Kim DS: A new system of generalized nonlinear mixed variational inequalities in Hilbert spaces. Journal of Convex Analysis 2004,11(1):235–243.
Cho YJ, Fang YP, Huang NJ, Hwang HJ: Algorithms for systems of nonlinear variational inequalities. Journal of the Korean Mathematical Society 2004,41(3):489–499.
Agarwal RP, Cho YJ, Huang NJ: Sensitivity analysis for strongly nonlinear quasi-variational inclusions. Applied Mathematics Letters 2000,13(6):19–24. 10.1016/S0893-9659(00)00048-3
Kazmi KR, Bhat MI: Iterative algorithm for a system of nonlinear variational-like inclusions. Computers& Mathematics with Applications 2004,48(12):1929–1935. 10.1016/j.camwa.2004.02.009
Fang YP, Huang NJ: -monotone operators and system of variational inclusions. Communications on Applied Nonlinear Analysis 2004,11(1):93–101.
Yan W-Y, Fang Y-P, Huang N-J: A new system of set-valued variational inclusions with -monotone operators. Mathematical Inequalities & Applications 2005,8(3):537–546.
Zou Y-Z, Huang N-J: -accretive operator with an application for solving variational inclusions in Banach spaces. Applied Mathematics and Computation 2008,204(2):809–816. 10.1016/j.amc.2008.07.024
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Zou Y-Z, Huang N-J: A new system of variational inclusions involving -accretive operator in Banach spaces. Applied Mathematics and Computation 2009,212(1):135–144. 10.1016/j.amc.2009.02.007
Verma RU: Generalized system for relaxed cocoercive variational inequalities and projection methods. Journal of Optimization Theory and Applications 2004,121(1):203–210.
Chang S-S, Cho YJ, Zhou H: Iterative Methods for Nonlinear Operator Equations in Banach Spaces. Nova Science, Huntington, NY, USA; 2002:xiv+459.
Weng X: Fixed point iteration for local strictly pseudo-contractive mapping. Proceedings of the American Mathematical Society 1991,113(3):727–731. 10.1090/S0002-9939-1991-1086345-8
Agarwal RP, Huang N-J, Tan M-Y: Sensitivity analysis for a new system of generalized nonlinear mixed quasi-variational inclusions. Applied Mathematics Letters 2004,17(3):345–352. 10.1016/S0893-9659(04)90073-0
Huang N-J, Fang Y-P: A new class of general variational inclusions involving maximal -monotone mappings. Publicationes Mathematicae Debrecen 2003,62(1–2):83–98.
Jin M-M: Perturbed algorithm and stability for strongly nonlinear quasi-variational inclusion involving -accretive operators. Mathematical Inequalities & Applications 2006,9(4):771–779.
Peng J, Yang X: On existence of a solution for the system of generalized vector quasi-equilibrium problems with upper semicontinuous set-valued maps. International Journal of Mathematics and Mathematical Sciences 2005, (15):2409–2420.
Horn RA, Johnson CR: Matrix Analysis. Cambridge University Press, Cambridge, UK; 1985:xiii+561.
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Acknowledgment
The authors acknowledge the support of the Educational Science Foundation of Chongqing, Chongqing (KJ091315).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, HG., Xu, A. & Jin, M. A Hybrid Proximal Point Three-Step Algorithm for Nonlinear Set-Valued Quasi-Variational Inclusions System Involving 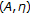 -Accretive Mappings.
Fixed Point Theory Appl 2010, 635382 (2010). https://doi.org/10.1155/2010/635382
-Accretive Mappings.
Fixed Point Theory Appl 2010, 635382 (2010). https://doi.org/10.1155/2010/635382
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/635382
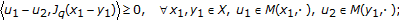
 ,
, 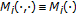 ,
, 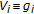 ,
,  ,
,  and
and 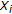 is a Hilbert space, then the problem (3.2) reduces to the problem associated with the system of variational inclusions with
is a Hilbert space, then the problem (3.2) reduces to the problem associated with the system of variational inclusions with 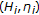 -monotone operators, which is finding
-monotone operators, which is finding  such that
such that  ,
, 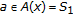 ,
, 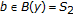 ,
, 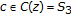 ,
,  ,
,  ,
, 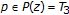 ,
,  ,
, 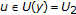 ,
, 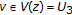 and
and 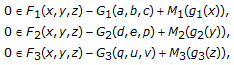
 ,
, 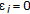 ,
,  (Hilbert space) and,
(Hilbert space) and, 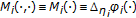 , where
, where  is a proper,
is a proper,  -subdifferentiable functional and
-subdifferentiable functional and 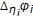 denotes the
denotes the 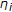 -subdifferential operator of
-subdifferential operator of 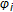 , then problem(3.3) changes to the problem associated with the following system of variational-like inequalities, which is finding
, then problem(3.3) changes to the problem associated with the following system of variational-like inequalities, which is finding 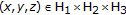 such that
such that 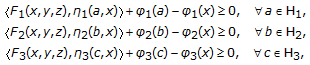
 ,
,  ,
, 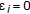 ,
, 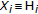 (Hilbert space) and
(Hilbert space) and 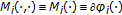 , where
, where 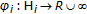 is a proper, convex, lower semicontinuous functional and
is a proper, convex, lower semicontinuous functional and  denotes the subdifferential operator of
denotes the subdifferential operator of 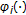 , then problem (3.3) changes to the problem associated with the following system of variational inequalities, which is finding
, then problem (3.3) changes to the problem associated with the following system of variational inequalities, which is finding 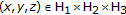 such that
such that 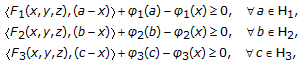
 ,
, 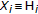 (Hilbert space), and
(Hilbert space), and 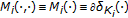 , where
, where 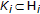 is a nonempty, closed, and convex subsets and
is a nonempty, closed, and convex subsets and 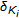 denotes the indicator of
denotes the indicator of  , then problem (3.5) reduces to the problem associated with the following system of variational inequalities, which is finding
, then problem (3.5) reduces to the problem associated with the following system of variational inequalities, which is finding  such that
such that 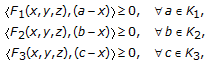
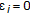 , and
, and 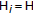 is a Hilbert space,
is a Hilbert space, 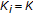 is a nonempty, closed and convex subset, for all
is a nonempty, closed and convex subset, for all 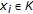 ,
,  , where
, where 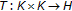 is a mapping on
is a mapping on 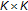 ,
, 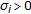 is a constant, then problem (3.6) changes to the following problem: find
is a constant, then problem (3.6) changes to the following problem: find  such that
such that