- Research Article
- Open access
- Published:
On Fixed Points of Maximalizing Mappings in Posets
Fixed Point Theory and Applications volume 2010, Article number: 634109 (2009)
Abstract
We use chain methods to prove fixed point results for maximalizing mappings in posets. Concrete examples are also presented.
1. Introduction
According to Bourbaki's fixed point theorem (cf. [1, 2]) a mapping  from a partially ordered set
from a partially ordered set  into itself has a fixed point if
into itself has a fixed point if  is extensive, that is,
is extensive, that is,  for all
for all  , and if every nonempty chain of
, and if every nonempty chain of  has the supremum in
has the supremum in  . In [3, Theorem
. In [3, Theorem  ] the existence of a fixed point is proved for a mapping
] the existence of a fixed point is proved for a mapping  which isascending, that is,
which isascending, that is,  implies
implies  . It is easy to verify that every extensive mapping is ascending. In [4] the existence of a fixed point of
. It is easy to verify that every extensive mapping is ascending. In [4] the existence of a fixed point of  is proved if
is proved if  for some
for some  , and if
, and if  issemi-increasing upward, that is,
issemi-increasing upward, that is,  whenever
whenever  and
and  . This property holds, for instance, if
. This property holds, for instance, if  is ascending orincreasing, that is,
is ascending orincreasing, that is,  whenever
whenever  .
.
In this paper we prove further generalizations to Bourbaki's fixed point theorem by assuming that a mapping  ismaximalizing, that is,
ismaximalizing, that is,  is a maximal element of
is a maximal element of  for all
for all  . Concrete examples of maximalizing mappings
. Concrete examples of maximalizing mappings  which have or do not have fixed points are presented. Chain methods introduced in [5, 6] are used in the proofs. These methods are also compared with three other chain methods.
which have or do not have fixed points are presented. Chain methods introduced in [5, 6] are used in the proofs. These methods are also compared with three other chain methods.
2. Preliminaries
A nonempty set  , equipped with a reflexive, antisymmetric, and transitive relation
, equipped with a reflexive, antisymmetric, and transitive relation  in
in  , is called a partially ordered set (poset). An element
, is called a partially ordered set (poset). An element  of a poset
of a poset  is called an upper bound of a subset
is called an upper bound of a subset  of
of  if
if  for each
for each  . If
. If  , we say that
, we say that  is thegreatest element of
is thegreatest element of  , and denote
, and denote  . A lower bound of
. A lower bound of  and the least element,
and the least element,  , of
, of  are defined similarly, replacing
are defined similarly, replacing  above by
above by  . If the set of all upper bounds of
. If the set of all upper bounds of  has the least element, we call it thesupremum of
has the least element, we call it thesupremum of and denote it by
and denote it by  . We say that
. We say that  is amaximal element of
is amaximal element of  if
if  , and if
, and if  and
and  imply that
imply that  . The infimum of
. The infimum of  ,
,  , and a minimal element of
, and a minimal element of  are defined similarly. A subset
are defined similarly. A subset  of
of  is called a chain if
is called a chain if  or
or  for all
for all  . We say that
. We say that  is well ordered if nonempty subsets of
is well ordered if nonempty subsets of  have least elements. Every well-ordered set is a chain.
have least elements. Every well-ordered set is a chain.
Let  be a nonempty poset. A basis to our considerations is the following chain method (cf. [6, Lemma
be a nonempty poset. A basis to our considerations is the following chain method (cf. [6, Lemma  ]).
]).
Lemma 2.1.
Given  and
and  , there exists a unique well-ordered chain
, there exists a unique well-ordered chain  in
in  , called a w-o chain of
, called a w-o chain of  -iterations, satisfying
-iterations, satisfying

If  exists in
exists in  , then
, then  , and
, and  .
.
The following result helps to analyze the w-o chain of  -iterations.
-iterations.
Lemma 2.2.
Let  and
and  be nonempty subsets of
be nonempty subsets of  . If
. If  and
and  exist, then the equation
exist, then the equation

is valid whenever either of its sides is defined.
Proof.
The sets  and
and  have same upper bounds, which implies the assertion.
have same upper bounds, which implies the assertion.
A subset  of a chain
of a chain  is called aninitial segment of
is called aninitial segment of  if
if  ,
,  and
and  imply
imply  . If
. If  is well ordered, then every element
is well ordered, then every element  of
of  which is not the possible maximum of
which is not the possible maximum of  has a successor:
has a successor:  , in
, in  . The next result gives a characterization of elements of the w-o chain of
. The next result gives a characterization of elements of the w-o chain of  -iterations.
-iterations.
Lemma 2.3.
Given  and
and  , let
, let  be the w-o chain of
be the w-o chain of  -iterations. Then the elements of
-iterations. Then the elements of  have the following properties.
have the following properties.
 .
.
An element  of
of  has a successor in
has a successor in  if and only if
if and only if  exists and
exists and  , and then
, and then  .
.
If  is an initial segment of
is an initial segment of  and
and  exists, then
exists, then  .
.
If  and
and  is not a successor, then
is not a successor, then  .
.
If  exists, then
exists, then  .
.
Proof.
-
(a)
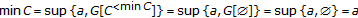 .
. -
(b)
Assume first that
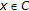 , and that
, and that 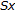 exists in
exists in  . Applying (2.1), Lemma 2.2, and the definition of
. Applying (2.1), Lemma 2.2, and the definition of 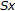 we obtain
we obtain

Moreover,  , by definition, whence
, by definition, whence  .
.
Assume next that  , that
, that  exists, and that
exists, and that  . The previous proof implies the following
. The previous proof implies the following
-
(i)
There is no element
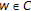 which satisfies
which satisfies 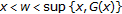 .
.
Then  , so that
, so that

Thus  by (2.1). This result and (i) imply that
by (2.1). This result and (i) imply that  .
.
-
(c)
Assume that
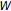 is an initial segment of
is an initial segment of  , and that
, and that 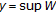 exists. If there is
exists. If there is 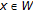 such that
such that  , then
, then 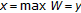 , so that
, so that  . Assume next that every element
. Assume next that every element  of
of 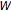 has the successor
has the successor 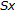 in
in 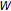 . Since
. Since  by (b), then
by (b), then 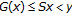 . This holds for all
. This holds for all  . Since
. Since 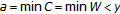 , then
, then 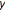 is an upper bound of
is an upper bound of  . If
. If  is an upper bound of
is an upper bound of 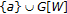 , then
, then  for every
for every 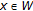 . Thus
. Thus  is an upper bound of
is an upper bound of 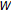 , whence
, whence 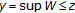 . But then
. But then 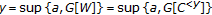 , so that
, so that 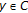 by (2.1).
by (2.1). -
(d)
Assume that
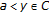 , and that
, and that 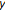 is not a successor of any element of
is not a successor of any element of  . Obviously,
. Obviously,  is an upper bound of
is an upper bound of 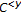 . Let
. Let  be an upper bound of
be an upper bound of 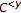 . If
. If 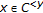 , then also
, then also 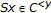 since
since 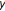 is not a successor. Because
is not a successor. Because 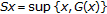 by (b), then
by (b), then  . This holds for every
. This holds for every  . Since also
. Since also  , then
, then  is an upper bound of
is an upper bound of 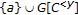 . Thus
. Thus 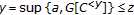 . This holds for every upper bound
. This holds for every upper bound  of
of  , whence
, whence 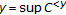 .
. -
(e)
If
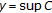 exists, then
exists, then 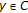 by (c) when
by (c) when 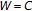 , whence
, whence 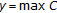 .
.
In the case when  we obtain the following result (cf. [7, Proposition
we obtain the following result (cf. [7, Proposition  ]).
]).
Lemma 2.4.
Given  and
and  , there exists a unique well-ordered chain
, there exists a unique well-ordered chain  in
in  , calleda w-o chain of
, calleda w-o chain of  -iterations of
-iterations of  , satisfying
, satisfying

If  , and if
, and if  exists, then
exists, then  , and
, and  .
.
Lemma 2.4 is in fact a special case of Lemma 2.1, since the assumption  implies that
implies that  equals to the w-o chain of
equals to the w-o chain of  -iterations. As for the use of
-iterations. As for the use of  in fixed point theory and in the theory of discontinuous differential and integral equations, see, for example, [8, 9] and the references therein.
in fixed point theory and in the theory of discontinuous differential and integral equations, see, for example, [8, 9] and the references therein.
3. Main Results
Let  be a nonempty poset. As an application of Lemma 2.1 we will prove our first existence result.
be a nonempty poset. As an application of Lemma 2.1 we will prove our first existence result.
Theorem 3.1.
A mapping  has a fixed point if
has a fixed point if  is maximalizing, that is,
is maximalizing, that is,  is a maximal element of
is a maximal element of  for all
for all  , and if
, and if  exists in
exists in  for some
for some  where
where  is the w-o chain of
is the w-o chain of  -iterations.
-iterations.
Proof.
If  is the w-o chain of
is the w-o chain of  -iterations, and if
-iterations, and if  exists in
exists in  , then
, then  and
and  by Lemma 2.1. Since
by Lemma 2.1. Since  is maximalizing, then
is maximalizing, then  , that is,
, that is,  is a fixed point of
is a fixed point of  .
.
The next result is a consequence of Theorem 3.1. and Lemma 2.3(e).
Proposition 3.2.
Assume that  is maximalizing. Given
is maximalizing. Given  , let
, let  be the w-o chain of
be the w-o chain of  -iterations. If
-iterations. If  exists, it is a fixed point of
exists, it is a fixed point of  if and only if
if and only if  exists.
exists.
Proof.
Assume that  exists. It follows from Lemma 2.3(e) that
exists. It follows from Lemma 2.3(e) that  . If
. If  is a fixed point of
is a fixed point of  , that is,
, that is,  , then
, then  , and
, and  .
.
Assume conversely that  exist. Applying (2.1) and Lemma 2.2 we obtain
exist. Applying (2.1) and Lemma 2.2 we obtain

Thus, by Theorem 3.1,  is a fixed point of
is a fixed point of  .
.
As a consequence of Proposition 3.2 we obtain the following result.
Corollary 3.3.
If nonempty chains of  have supremums, if
have supremums, if  is maximalizing, and if
is maximalizing, and if  exists for all
exists for all  , then for each
, then for each  the maximum of the w-o chain of
the maximum of the w-o chain of  -iterations exists and is a fixed point of
-iterations exists and is a fixed point of  .
.
Proof.
Let  be the w-o chain of
be the w-o chain of  -iterations. The given hypotheses imply that both
-iterations. The given hypotheses imply that both  and
and  exist. Thus the hypotheses of Proposition 3.2 are valid.
exist. Thus the hypotheses of Proposition 3.2 are valid.
The results of Lemma 2.3 are valid also when  is replaced by the w-o chain
is replaced by the w-o chain  of
of  -iterations of
-iterations of  . As a consequence of these results and Lemma 2.4 we obtain the following generalizations to Bourbaki's fixed point theorem.
. As a consequence of these results and Lemma 2.4 we obtain the following generalizations to Bourbaki's fixed point theorem.
Theorem 3.4.
Assume that  is maximalizing, and that
is maximalizing, and that  for some
for some  , and let
, and let  be the w-o chain of
be the w-o chain of  -iterations of
-iterations of  .
.
-
(a)
If
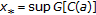 exists, then
exists, then 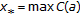 , and
, and 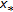 is a fixed point of
is a fixed point of  .
. -
(b)
If
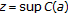 exists, it is a fixed point of
exists, it is a fixed point of 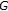 if and only if
if and only if 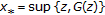 exists.
exists. -
(c)
If nonempty chains of
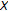 have supremums, and if
have supremums, and if 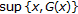 exists for all
exists for all  , then
, then 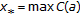 exists, and
exists, and 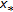 is a fixed point of
is a fixed point of 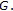
The previous results have obvious duals, which imply the following results.
Theorem 3.5.
A mapping  has a fixed point if
has a fixed point if  is minimalizing, that is,
is minimalizing, that is,  is a minimal element of
is a minimal element of  for all
for all  , and if
, and if  exists in
exists in  for some
for some  whenever
whenever  is a nonempty chain in
is a nonempty chain in  .
.
Theorem 3.6.
A minimalizing mapping  has a fixed point if
has a fixed point if  exists whenever
exists whenever  is a nonempty chain in
is a nonempty chain in  , and if
, and if  for some
for some  .
.
Proposition 3.7.
A minimalizing mapping  has a fixed point if every nonempty chain
has a fixed point if every nonempty chain  has the infimum in
has the infimum in  , and if
, and if  exists for all
exists for all  .
.
Remark 3.8.
The hypothesis that  is maximalizing can be weakened in Theorems 3.1 and 3.4 and in Proposition 3.2 to the form:
is maximalizing can be weakened in Theorems 3.1 and 3.4 and in Proposition 3.2 to the form:  is maximalizing, that is,
is maximalizing, that is,  is a maximal element of
is a maximal element of  .
.
4. Examples and Remarks
We will first present an example of a maximalizing mapping whose fixed point is obtained as the maximum of the w-o chain of  -iterations.
-iterations.
Example 4.1.
Let  be a closed disc
be a closed disc  , ordered coordinate-wise. Let
, ordered coordinate-wise. Let  denote the greatest integer
denote the greatest integer  when
when  . Define a function
. Define a function  by
by

It is easy to verify that  , and that
, and that  is maximalizing. To find a fixed point of
is maximalizing. To find a fixed point of  , choose
, choose  . It follows from Lemma 2.3(b) that the first elements of the w-o chain of
. It follows from Lemma 2.3(b) that the first elements of the w-o chain of  -iterations are successive approximations
-iterations are successive approximations

as long as  is defined. Denoting
is defined. Denoting  , these successive approximations can be rewritten in the form
, these successive approximations can be rewritten in the form

as long as  and
and  , and at least one of these inequalities is strict. Elementary calculations show that
, and at least one of these inequalities is strict. Elementary calculations show that  , for every
, for every  . Thus (4.3) can be rewritten as
. Thus (4.3) can be rewritten as

Since the function  is increasing
is increasing  , then
, then  for every
for every  . Thus (4.4) can be reduced to the form
. Thus (4.4) can be reduced to the form

The sequence  is strictly increasing, whence also
is strictly increasing, whence also  is strictly increasing by (4.5). Thus the set
is strictly increasing by (4.5). Thus the set  is an initial segment of
is an initial segment of  . Moreover,
. Moreover,  , and if
, and if  , then
, then  . Since
. Since  is bounded above by
is bounded above by  , then
, then  exists, and
exists, and  . Thus
. Thus  , and it belongs to
, and it belongs to  , whence
, whence  by Lemma 2.3(c). To determine
by Lemma 2.3(c). To determine  , notice that
, notice that  by (4.5). Thus
by (4.5). Thus  , or equivalently,
, or equivalently,  , so that
, so that  . Since
. Since  , then
, then  by Lemma 2.3(c). Because
by Lemma 2.3(c). Because  is a maximal element of
is a maximal element of  , then
, then  . Moreover,
. Moreover,  , so that
, so that  is a fixed point of
is a fixed point of  .
.
The first  elements of the w-o chain
elements of the w-o chain  of
of  -iterations can be estimated by the following Maple program (floor
-iterations can be estimated by the following Maple program (floor ):
):
 (1,1-floor(u) + floor(v)):
(1,1-floor(u) + floor(v)):  (floor
(floor )/2:
)/2:  :
:
for  to
to  do
do  (max
(max , evalf(max
, evalf(max );
);  end do;
end do;
For instance,  .
.
The verification of the following properties are left to the reader.
-
(i)
If
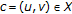 ,
, 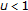 , and
, and 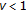 , then the elements of w-o chain
, then the elements of w-o chain  of
of  -iterations, after two first terms if
-iterations, after two first terms if  , are of the form
, are of the form 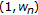 ,
, 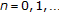 , where
, where 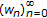 is increasing and converges to
is increasing and converges to 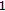 . Thus
. Thus  is the maximum of
is the maximum of  and a fixed point of
and a fixed point of 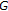 .
. -
(ii)
If
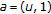 ,
, 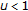 , or
, or 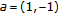 , then
, then 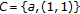 .
. -
(iii)
If
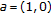 , then
, then 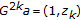 and
and 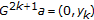 ,
,  , where the sequences
, where the sequences 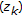 and
and  are bounded and increasing. The limit
are bounded and increasing. The limit  of
of 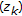 is the smaller real root of
is the smaller real root of 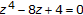 ;
; 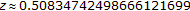 , and the limit
, and the limit 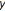 of
of  is
is 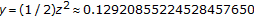 . Moreover
. Moreover 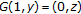 and
and 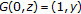 , whence no subsequence of the iteration
, whence no subsequence of the iteration  converges to a fixed point of
converges to a fixed point of 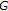 .
. -
(iv)
For any choice of
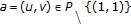 the iterations
the iterations 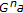 and
and 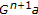 are not order related when
are not order related when 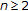 . The sequence
. The sequence  does not converge, and no subsequence of it converges to a fixed point of
does not converge, and no subsequence of it converges to a fixed point of 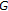 .
. -
(v)
Denote
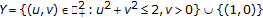 . The function
. The function  , defined by (4.1), satisfies
, defined by (4.1), satisfies  and is maximalizing. The maximum of the w-o chain of
and is maximalizing. The maximum of the w-o chain of 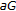 -iterations with
-iterations with 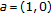 is
is 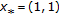 , and
, and 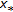 is a fixed point of
is a fixed point of 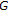 . If
. If  , then
, then  and
and 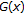 are not comparable.
are not comparable.
The following example shows that  need not to have a fixed point if either of the hypothesis of Theorem 3.1 is not valid.
need not to have a fixed point if either of the hypothesis of Theorem 3.1 is not valid.
Example 4.2.
Denote  and
and  , where
, where  and
and  are as in Example 4.1. Choose
are as in Example 4.1. Choose  , and let
, and let  be defined by (4.1).
be defined by (4.1).  is maximalizing, but
is maximalizing, but  has no fixed points, since
has no fixed points, since  and
and  . The last hypothesis of Theorem 3.1 is not satisfied.
. The last hypothesis of Theorem 3.1 is not satisfied.
Denoting  , then the set
, then the set  is a complete join lattice, that is, every nonempty subset of
is a complete join lattice, that is, every nonempty subset of  has the supremum in
has the supremum in  . Let
. Let  satisfy
satisfy  and
and  .
.  has no fixed points, but
has no fixed points, but  is not maximalizing, since
is not maximalizing, since  .
.
Example 4.3.
The components  ,
,  of the fixed point of
of the fixed point of  in Example 4.1 form also a solution of the system
in Example 4.1 form also a solution of the system

Moreover a Maple program introduced in Example 4.1 serves a method to estimate this solution. When  , the estimate is
, the estimate is  ,
,  .
.
Remark 4.4.
The standard "solve" and "fsolve" commands of Maple 12 do not give a solution or its approximation for the system of Example 4.3.
In Example 4.1 the mapping  is nonincreasing, nonextensive, nonascending, not semiincreasing upward, and noncontinuous.
is nonincreasing, nonextensive, nonascending, not semiincreasing upward, and noncontinuous.
Chain  is compared in [10] with three other chains which generalize the sequence of ordinary iterations
is compared in [10] with three other chains which generalize the sequence of ordinary iterations  , and which are used to prove fixed point results for
, and which are used to prove fixed point results for  . These chains are the generalized orbit
. These chains are the generalized orbit  defined in [10] (being identical with the set
defined in [10] (being identical with the set  defined in [11]), the smallest admissible set
defined in [11]), the smallest admissible set  containing
containing  (cf. [12–14]), and the smallest complete
(cf. [12–14]), and the smallest complete  -chain
-chain  containing
containing  (cf. [10, 15]). If
(cf. [10, 15]). If  is extensive, and if nonempty chains of
is extensive, and if nonempty chains of  have supremums, then
have supremums, then  , and
, and  is their cofinal subchain (cf. [10, Corollary
is their cofinal subchain (cf. [10, Corollary  ]). The common maximum
]). The common maximum  of these four chains is a fixed point of
of these four chains is a fixed point of  . This result implies Bourbaki's Fixed Point Theorem.
. This result implies Bourbaki's Fixed Point Theorem.
On the other hand, if the hypotheses of Theorem 3.4 hold and  , then
, then  and
and  are not necessarily comparable. The successor of such an
are not necessarily comparable. The successor of such an  in
in  is
is  by [14, Proposition
by [14, Proposition  ]. In such a case the chains
]. In such a case the chains  ,
,  and
and  attain neither
attain neither  nor any fixed point of
nor any fixed point of  . For instance when
. For instance when  in Example 4.1, then
in Example 4.1, then  , where
, where  is the w-o chain of
is the w-o chain of  -iterations. Since
-iterations. Since  , then
, then  does not exist,
does not exist,  (see [10]). Thus only
(see [10]). Thus only  attains a fixed point of
attains a fixed point of  as its maximum. As shown in Example 4.1, the consecutive elements of the iteration sequence
as its maximum. As shown in Example 4.1, the consecutive elements of the iteration sequence  are unordered, and their limits are not fixed points of
are unordered, and their limits are not fixed points of  . Hence, in these examples also finite combinations of chains
. Hence, in these examples also finite combinations of chains  used in [16, Theorem
used in [16, Theorem  ] to prove a fixed point result are insufficient to attain a fixed point of
] to prove a fixed point result are insufficient to attain a fixed point of  .
.
Neither the above-mentioned four chains nor their duals are available to find fixed points of  if
if  and
and  are unordered. For instance, they cannot be applied to prove Theorems 3.1 and 3.5 or Propositions 3.2 and 3.7.
are unordered. For instance, they cannot be applied to prove Theorems 3.1 and 3.5 or Propositions 3.2 and 3.7.
References
Bourbaki N: Eléments de Mathématique, I. Théorie des Ensembles, Fascicule de Résultats, Actualités Scientifiques et Industrielles, no. 846. Hermann, Paris, France; 1939.
Kirk WA: Fixed Point Theory: A Brief Survey, Notas de Matematicas, no. 108. Universidas de Los Andes, Mérida, Venezuela; 1990.
Klimeš J: A characterization of inductive posets. Archivum Mathematicum 1985,21(1):39–42.
Heikkilä S: Fixed point results for semi-increasing mappings. to appear in Nonlinear Studies
Heikkilä S: Monotone methods with applications to nonlinear analysis. In Proceedings of the 1st World Congress of Nonlinear Analysts, 1996, Tampa, Fla, USA. Volume 1. Walter de Gruyter; 2147–2158.
Heikkilä S: A method to solve discontinuous boundary value problems. Nonlinear Analysis 2001, 47: 2387–2394. 10.1016/S0362-546X(01)00362-5
Heikkilä S: On recursions, iterations and well-orderings. Nonlinear Times and Digest 1995,2(1):117–123.
Carl S, Heikkilä S: Nonlinear Differential Equations in Ordered Spaces. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2000.
Heikkilä S, Lakshmikantham V: Monotone Iterative Techniques for Discontinuous Nonlinear Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 181. Marcel Dekker, New York, NY, USA; 1994:xii+514.
Manka R: On generalized methods of successive approximations. to appear in Nonlinear Analysis
Abian S, Brown AB: A theorem on partially ordered sets, with applications to fixed point theorems. Canadian Journal of Mathematics 1961, 13: 78–82. 10.4153/CJM-1961-007-5
Büber T, Kirk WA: A constructive proof of a fixed point theorem of Soardi. Mathematica Japonica 1995,41(2):233–237.
Büber T, Kirk WA: Constructive aspects of fixed point theory for nonexpansive mappings. In Proceedings of the 1st World Congress of Nonlinear Analysts, 1996, Tampa, Fla, USA. Volume 1. Walter de Gruyter; 2115–2125.
Heikkilä S: On chain methods used in fixed point theory. Nonlinear Studies 1999,6(2):171–180.
Fuchssteiner B: Iterations and fixpoints. Pacific Journal of Mathematics 1977,68(1):73–80.
Baclawski K, Björner A: Fixed points in partially ordered sets. Advances in Mathematics 1979,31(3):263–287. 10.1016/0001-8708(79)90045-8
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Heikkilä, S. On Fixed Points of Maximalizing Mappings in Posets. Fixed Point Theory Appl 2010, 634109 (2009). https://doi.org/10.1155/2010/634109
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/634109
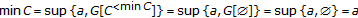 .
.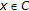 , and that
, and that 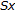 exists in
exists in  . Applying (2.1), Lemma 2.2, and the definition of
. Applying (2.1), Lemma 2.2, and the definition of 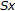 we obtain
we obtain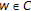 which satisfies
which satisfies 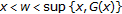 .
.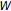 is an initial segment of
is an initial segment of  , and that
, and that 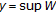 exists. If there is
exists. If there is 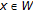 such that
such that  , then
, then 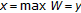 , so that
, so that  . Assume next that every element
. Assume next that every element  of
of 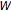 has the successor
has the successor 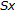 in
in 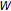 . Since
. Since  by (b), then
by (b), then 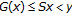 . This holds for all
. This holds for all  . Since
. Since 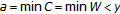 , then
, then 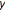 is an upper bound of
is an upper bound of  . If
. If  is an upper bound of
is an upper bound of 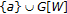 , then
, then  for every
for every 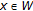 . Thus
. Thus  is an upper bound of
is an upper bound of 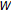 , whence
, whence 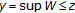 . But then
. But then 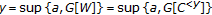 , so that
, so that 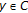 by (2.1).
by (2.1).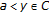 , and that
, and that 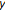 is not a successor of any element of
is not a successor of any element of  . Obviously,
. Obviously,  is an upper bound of
is an upper bound of 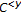 . Let
. Let  be an upper bound of
be an upper bound of 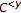 . If
. If 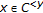 , then also
, then also 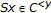 since
since 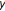 is not a successor. Because
is not a successor. Because 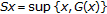 by (b), then
by (b), then  . This holds for every
. This holds for every  . Since also
. Since also  , then
, then  is an upper bound of
is an upper bound of 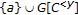 . Thus
. Thus 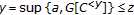 . This holds for every upper bound
. This holds for every upper bound  of
of  , whence
, whence 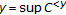 .
.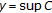 exists, then
exists, then 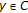 by (c) when
by (c) when 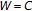 , whence
, whence 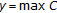 .
.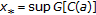 exists, then
exists, then 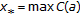 , and
, and 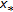 is a fixed point of
is a fixed point of  .
.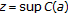 exists, it is a fixed point of
exists, it is a fixed point of 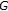 if and only if
if and only if 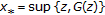 exists.
exists.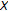 have supremums, and if
have supremums, and if 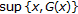 exists for all
exists for all  , then
, then 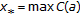 exists, and
exists, and 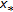 is a fixed point of
is a fixed point of 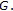
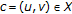 ,
, 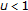 , and
, and 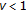 , then the elements of w-o chain
, then the elements of w-o chain  of
of  -iterations, after two first terms if
-iterations, after two first terms if  , are of the form
, are of the form 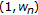 ,
, 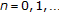 , where
, where 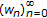 is increasing and converges to
is increasing and converges to 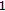 . Thus
. Thus  is the maximum of
is the maximum of  and a fixed point of
and a fixed point of 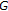 .
.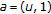 ,
, 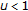 , or
, or 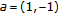 , then
, then 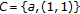 .
.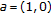 , then
, then 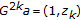 and
and 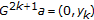 ,
,  , where the sequences
, where the sequences 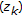 and
and  are bounded and increasing. The limit
are bounded and increasing. The limit  of
of 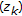 is the smaller real root of
is the smaller real root of 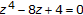 ;
; 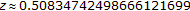 , and the limit
, and the limit 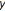 of
of  is
is 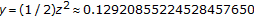 . Moreover
. Moreover 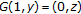 and
and 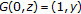 , whence no subsequence of the iteration
, whence no subsequence of the iteration  converges to a fixed point of
converges to a fixed point of 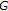 .
.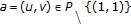 the iterations
the iterations 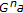 and
and 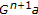 are not order related when
are not order related when 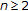 . The sequence
. The sequence  does not converge, and no subsequence of it converges to a fixed point of
does not converge, and no subsequence of it converges to a fixed point of 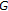 .
.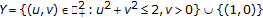 . The function
. The function  , defined by (4.1), satisfies
, defined by (4.1), satisfies  and is maximalizing. The maximum of the w-o chain of
and is maximalizing. The maximum of the w-o chain of 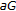 -iterations with
-iterations with 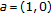 is
is 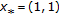 , and
, and 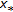 is a fixed point of
is a fixed point of 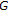 . If
. If  , then
, then  and
and 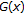 are not comparable.
are not comparable.