- Research Article
- Open access
- Published:
An Iterative Algorithm for Mixed Equilibrium Problems and Variational Inclusions Approach to Variational Inequalities
Fixed Point Theory and Applications volume 2010, Article number: 564361 (2010)
Abstract
We present an iterative algorithm for finding a common element  of the set of solutions of a mixed equilibrium problem and the set of a variational inclusion in a real Hilbert space. Furthermore, we prove that the proposed iterative algorithms strongly converge to
of the set of solutions of a mixed equilibrium problem and the set of a variational inclusion in a real Hilbert space. Furthermore, we prove that the proposed iterative algorithms strongly converge to  which solves some variational inequality.
which solves some variational inequality.
1. Introduction
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a nonlinear mapping, let
be a nonlinear mapping, let  be a function, and let
be a function, and let  be a bifunction of
be a bifunction of  into
into  . Now we consider the following mixed equilibrium problem:
. Now we consider the following mixed equilibrium problem:

The set of solution of problem (1.1) is denoted by EP.
If  , then the mixed equilibrium problem (1.1) becomes the following mixed equilibrium problem:
, then the mixed equilibrium problem (1.1) becomes the following mixed equilibrium problem:

which was considered by Ceng and Yao [1]. If  , then the mixed equilibrium problem (1.1) becomes the following equilibrium problem:
, then the mixed equilibrium problem (1.1) becomes the following equilibrium problem:

which was studied by S. Takahashi and W. Takahashi [2]. If  and
and  , then the mixed equilibrium problem (1.1) becomes the following equilibrium problem:
, then the mixed equilibrium problem (1.1) becomes the following equilibrium problem:

If  for all
for all  , the mixed equilibrium problem (1.1) becomes the following variational inequality problem:
, the mixed equilibrium problem (1.1) becomes the following variational inequality problem:

The mixed equilibrium problems include fixed point problems, optimization problems, variational inequality problems, Nash equilibrium problems, and the equilibrium problems as special cases; see, for example, [3–8]. Some methods have been proposed to solve the mixed equilibrium problem and the equilibrium problem. In 1997, Flaim and Antipen [4] introduced an iterative method of finding the best approximation to the initial data and proved a strong convergence theorem. Subsequently, S. Takahashi and W. Takahashi [9] introduced another iterative scheme for finding a common element of the set of solutions of the equilibrium problem (1.2) and the set of fixed point points of a nonexpansive mapping. Furthermore, Yao et al. [10] introduced some new iterative schemes for finding a common element of the set of solutions of the equilibrium problem (1.2) and the set of common fixed points of finitely (infinitely) nonexpansive mappings. Very recently, Ceng and Yao [1] considered a new iterative scheme for finding a common element of the set of solutions of the mixed equilibrium problem and the set of common fixed points of finitely many nonexpansive mappings. Peng and Yao [11] developed a CQ method. They obtained some strong convergence results for finding a common element of the set of solutions of the mixed equilibrium problem (1.1) and the set of the variational inequality and the set of fixed points of a nonexpansive mapping. Their results extend and improve the corresponding results in [1, 9, 12].
Recall that a mapping  is said to be
is said to be  -inverse strongly monotone if there exists a constant
-inverse strongly monotone if there exists a constant  such that
such that  for all
for all  . A mapping
. A mapping  is strongly positive on
is strongly positive on  if there exists a constant
if there exists a constant  such that
such that  .
.
Let  be a single-valued nonlinear mapping and let
be a single-valued nonlinear mapping and let  be a set-valued mapping. Now we concern the following variational inclusion, which is to find a point
be a set-valued mapping. Now we concern the following variational inclusion, which is to find a point  such that
such that

where  is the zero vector in
is the zero vector in  . The set of solutions of problem (1.6) is denoted by
. The set of solutions of problem (1.6) is denoted by  . If
. If  , then problem (1.6) becomes the generalized equation introduced by Robinson [13]. If
, then problem (1.6) becomes the generalized equation introduced by Robinson [13]. If  , then problem (1.6) becomes the inclusion problem introduced by Rockafellar [14]. It is known that (1.6) provides a convenient framework for the unified study of optimal solutions in many optimization related areas including mathematical programming, complementarity, variational inequalities, optimal control, mathematical economics, equilibria, and game theory. Also various types of variational inclusions problems have been extended and generalized. Recently, Zhang et al. [15] introduced a new iterative scheme for finding a common element of the set of solutions to the problem (1.6) and the set of fixed points of nonexpansive mappings in Hilbert spaces. Peng et al. [16] introduced another iterative scheme by the viscosity approximate method for finding a common element of the set of solutions of a variational inclusion with set-valued maximal monotone mapping and inverse strongly monotone mappings, the set of solutions of an equilibrium problem, and the set of fixed points of a nonexpansive mapping. For some related works, please see [1, 2, 9–11, 13–34] and the references therein.
, then problem (1.6) becomes the inclusion problem introduced by Rockafellar [14]. It is known that (1.6) provides a convenient framework for the unified study of optimal solutions in many optimization related areas including mathematical programming, complementarity, variational inequalities, optimal control, mathematical economics, equilibria, and game theory. Also various types of variational inclusions problems have been extended and generalized. Recently, Zhang et al. [15] introduced a new iterative scheme for finding a common element of the set of solutions to the problem (1.6) and the set of fixed points of nonexpansive mappings in Hilbert spaces. Peng et al. [16] introduced another iterative scheme by the viscosity approximate method for finding a common element of the set of solutions of a variational inclusion with set-valued maximal monotone mapping and inverse strongly monotone mappings, the set of solutions of an equilibrium problem, and the set of fixed points of a nonexpansive mapping. For some related works, please see [1, 2, 9–11, 13–34] and the references therein.
Inspired and motivated by the works in the literature, in this paper, we present an iterative algorithm for finding a common element  of the set of solutions of a mixed equilibrium problem and the set of a variational inclusion in a real Hilbert space. Furthermore, we prove that the proposed iterative algorithms strongly converge to
of the set of solutions of a mixed equilibrium problem and the set of a variational inclusion in a real Hilbert space. Furthermore, we prove that the proposed iterative algorithms strongly converge to  which solves some variational inequality.
which solves some variational inequality.
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Let
. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Then, for any
. Then, for any  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that

Such a  is called the metric projection of
is called the metric projection of  onto
onto  . We know that
. We know that  is nonexpansive. Further, for
is nonexpansive. Further, for  and
and  ,
,

A set-valued mapping  is called monotone if, for all
is called monotone if, for all  ,
,  and
and  imply
imply  . A monotone mapping
. A monotone mapping  is maximal if its graph
is maximal if its graph  is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping  is maximal if and only if, for
is maximal if and only if, for  ,
,  for every
for every  implies
implies  .
.
Let the set-valued mapping  be maximal monotone. We define the resolvent operator
be maximal monotone. We define the resolvent operator  associated with
associated with  and
and  as follows:
as follows:

where  is a positive number. It is worth mentioning that the resolvent operator
is a positive number. It is worth mentioning that the resolvent operator  is single-valued, nonexpansive, and 1-inverse strongly monotone and that a solution of problem (1.6) is a fixed point of the operator
is single-valued, nonexpansive, and 1-inverse strongly monotone and that a solution of problem (1.6) is a fixed point of the operator  for all
for all  , see, for instance, [25].
, see, for instance, [25].
Throughout this paper, we assume that a bifunction 
 and a convex function
and a convex function  satisfy the following conditions:
satisfy the following conditions:
(H1) for all
for all  ;
;
(H2) is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(H3)for each  ,
,  is weakly upper semicontinuous;
is weakly upper semicontinuous;
(H4)for each  ,
,  is convex and lower semicontinuous;
is convex and lower semicontinuous;
(H5)for each  and
and  , there exists a bounded subset
, there exists a bounded subset  and
and  such that for any
such that for any  ,
,

Lemma (see [11]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction and let
be a bifunction and let  be a proper lower semicontinuous and convex function. For
be a proper lower semicontinuous and convex function. For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

for all  . Assume that the conditions (H1)–(H5) hold. Then one has the following results:
. Assume that the conditions (H1)–(H5) hold. Then one has the following results:
(1)for each  ,
,  and
and  is single-valued;
is single-valued;
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,

(3) ;
;
(4) is closed and convex.
is closed and convex.
Lemma (see [24]).
Let  be a maximal monotone mapping and let
be a maximal monotone mapping and let  be a Lipschitz-continuous mapping. Then the mapping
be a Lipschitz-continuous mapping. Then the mapping  is maximal monotone.
is maximal monotone.
Lemma (see [34]).
Assume taht  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that  where
where  is a sequence in
is a sequence in  and
and  is a sequence such that
is a sequence such that
(1) ;
;
(2) or
or  .
.
Then  .
.
3. Main Results
In this section, we will prove our main result. First, we give some assumptions on the operators and the parameters. Subsequently, we introduce our iterative algorithm for finding a common element of the set of solutions of a mixed equilibrium problem and the set of a variational inclusion. Finally, we will show that the proposed algorithm has strong convergence.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a lower semicontinuous and convex function and let
be a lower semicontinuous and convex function and let  be a bifunction satisfying conditions (H1)–(H5). Let
be a bifunction satisfying conditions (H1)–(H5). Let  be a strongly positive bounded linear operator with coefficient
be a strongly positive bounded linear operator with coefficient  and let
and let  be a maximal monotone mapping. Let the mappings
be a maximal monotone mapping. Let the mappings  be
be  -inverse strongly monotone and
-inverse strongly monotone and  -inverse strongly monotone, respectively. Let
-inverse strongly monotone, respectively. Let  and
and  be two constants such that
be two constants such that  and
and  .
.
Now we introduce the following iteration algorithm.
Algorithm 3.1.
For given  arbitrarily, compute the sequences
arbitrarily, compute the sequences  and
and  as follows:
as follows:

where  is a real sequence in
is a real sequence in  .
.
Now we study the strong convergence of the algorithm (3.1).
Theorem 3.2.
Suppose that  . Assume the following conditions are satisfied:
. Assume the following conditions are satisfied:
(i) ;
;
(ii) ;
;
(iii) .
.
Then the sequence  generated by (3.1) converges strongly to
generated by (3.1) converges strongly to  which solves the following variational inequality:
which solves the following variational inequality:

Proof.
Take  . It is clear that
. It is clear that

We divide our proofs into the following five steps:
(1)the sequences  and
and  are bounded;
are bounded;
(2) ;
;
(3) ;
;
(4) ;
;
(5) .
.
Proof.
Since  is
is  -inverse strongly monotone and
-inverse strongly monotone and  is
is  -inverse strongly monotone, we have
-inverse strongly monotone, we have


It is clear that if  and
and  , then
, then  and
and  are all nonexpansive. Set
are all nonexpansive. Set  . It follows that
. It follows that

By Lemma 2.1, we have  for all
for all  . Then, we have
. Then, we have

Hence, we have

Since  is linear bounded self-adjoint operator on
is linear bounded self-adjoint operator on  , then
, then

Observe that

that is to say  is positive. It follows that
is positive. It follows that

From (3.1), we deduce that

Therefore,  is bounded. Hence,
is bounded. Hence,  ,
,  , and
, and  are all bounded.
are all bounded.
Proof.
From (3.1), we have

Note that

Substituting (3.14) into (3.13), we get

Notice that  This together with the last inequality and Lemma 2.3 implies that
This together with the last inequality and Lemma 2.3 implies that

Proof.
From (3.5) and (3.7), we get

By (3.1), we obtain

where  is some constant satisfying
is some constant satisfying  . From (3.17) and (3.18), we have
. From (3.17) and (3.18), we have

Thus,

which imply that

Proof.
Since  is firmly nonexpansive, we have
is firmly nonexpansive, we have

Hence, we have

Since  is 1-inverse strongly monotone, we have
is 1-inverse strongly monotone, we have

which implies that

Thus, by (3.23) and (3.25), we obtain

Substitute (3.26) into (3.18) to get

Then we derive

So, we have

Proof.
We note that  is a contraction. As a matter of fact,
is a contraction. As a matter of fact,

for all  . Hence
. Hence  has a unique fixed point, say
has a unique fixed point, say  . That is,
. That is,  . This implies that
. This implies that  for all
for all  . Next, we prove that
. Next, we prove that

First, we note that there exists a subsequence  of
of  such that
such that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  .
.
We next show that  . By
. By  , we know that
, we know that

It follows from (H2) that

Hence,

For  and
and  , let
, let  . From (3.35) we have
. From (3.35) we have

Since  , we have
, we have  . Further, from the inverse strongly monotonicity of
. Further, from the inverse strongly monotonicity of  , we have
, we have  . So, from (H4) and the weakly lower semicontinuity of
. So, from (H4) and the weakly lower semicontinuity of  ,
,  and
and  weakly, we have
weakly, we have

From (H1), (H4), and (3.37), we also have

and hence

Letting  , we have, for each
, we have, for each  ,
,

This implies that  .
.
Next, we show that  . In fact, since
. In fact, since  is
is  -inverse strongly monotone,
-inverse strongly monotone,  is Lipschitz continuous monotone mapping. It follows from Lemma 2.2 that
is Lipschitz continuous monotone mapping. It follows from Lemma 2.2 that  is maximal monotone. Let
is maximal monotone. Let  , that is,
, that is,  . Again since
. Again since  , we have
, we have  , that is,
, that is,  . By virtue of the maximal monotonicity of
. By virtue of the maximal monotonicity of  , we have
, we have

and so

It follows from  ,
,  and
and  that
that

It follows from the maximal monotonicity of  that
that  , that is,
, that is,  . Therefore,
. Therefore,  . It follows that
. It follows that

Proof.
First, we note that  ; then for all
; then for all  , we have
, we have  .
.
From (3.1), we have

that is,

where  and
and  . It is easy to see that
. It is easy to see that  and
and  . Hence, by Lemma 2.3, we conclude that the sequence
. Hence, by Lemma 2.3, we conclude that the sequence  converges strongly to
converges strongly to  . This completes the proof.
. This completes the proof.
References
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008,214(1):186–201. 10.1016/j.cam.2007.02.022
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2008,69(3):1025–1033. 10.1016/j.na.2008.02.042
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Flåm SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997,78(1):29–41.
Zeng L-C, Wu S-Y, Yao J-C: Generalized KKM theorem with applications to generalized minimax inequalities and generalized equilibrium problems. Taiwanese Journal of Mathematics 2006,10(6):1497–1514.
Chadli O, Wong NC, Yao JC: Equilibrium problems with applications to eigenvalue problems. Journal of Optimization Theory and Applications 2003,117(2):245–266. 10.1023/A:1023627606067
Chadli O, Schaible S, Yao JC: Regularized equilibrium problems with application to noncoercive hemivariational inequalities. Journal of Optimization Theory and Applications 2004,121(3):571–596.
Konnov IV, Schaible S, Yao JC: Combined relaxation method for mixed equilibrium problems. Journal of Optimization Theory and Applications 2005,126(2):309–322. 10.1007/s10957-005-4716-0
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Yao Y, Liou Y-C, Yao J-C: Convergence theorem for equilibrium problems and fixed point problems of infinite family of nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-12.
Peng J-W, Yao J-C: A new hybrid-extragradient method for generalized mixed equilibrium problems, fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2008,12(6):1401–1432.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Robinson SM: Generalized equations and their solutions. I. Basic theory. Mathematical Programming Study 1979, (10):128–141.
Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization 1976,14(5):877–898. 10.1137/0314056
Zhang S-S, Lee JHW, Chan CK: Algorithms of common solutions to quasi variational inclusion and fixed point problems. Applied Mathematics and Mechanics. English Edition 2008,29(5):571–581. 10.1007/s10483-008-0502-y
Peng J-W, Wang Y, Shyu DS, Yao J-C: Common solutions of an iterative scheme for variational inclusions, equilibrium problems, and fixed point problems. Journal of Inequalities and Applications 2008, 2008:-15.
Ding XP, Lin YC, Yao JC: Predictor-corrector algorithms for solving generalized mixed implicit quasi-equilibrium problems. Applied Mathematics and Mechanics 2006,27(9):1157–1164. 10.1007/s10483-006-0901-1
Plubtieng S, Punpaeng R: A general iterative method for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,336(1):455–469. 10.1016/j.jmaa.2007.02.044
Tada A, Takahashi W: Strong convergence theorem for an equilibrium problem and a nonexpansive mapping. In Nonlinear Analysis and Convex Analysis. Edited by: Takahashi W, Tanaka T. Yokohama Publishers, Yokohama, Japan; 2007:609–617.
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001,5(2):387–404.
Yao Y, Yao J-C: On modified iterative method for nonexpansive mappings and monotone mappings. Applied Mathematics and Computation 2007,186(2):1551–1558. 10.1016/j.amc.2006.08.062
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Adly S: Perturbed algorithms and sensitivity analysis for a general class of variational inclusions. Journal of Mathematical Analysis and Applications 1996,201(2):609–630. 10.1006/jmaa.1996.0277
Brézis H: Opérateurs Maximaux Monotones et Semi-Groupes de Contractions dans les Espaces de Hilbert, North-Holland Mathematics Studies, no. 5. North-Holland, Amsterdam, The Netherlands; 1973:vi+183.
Lemaire B: Which fixed point does the iteration method select? In Recent Advances in Optimization (Trier, 1996), Lecture Notes in Economics and Mathematical Systems. Volume 452. Springer, Berlin, Germany; 1997:154–167.
Yao Y, Liou Y-C: Weak and strong convergence of Krasnoselski-Mann iteration for hierarchical fixed point problems. Inverse Problems 2008,24(1):-8.
Yao Y, Liou Y-C, Yao J-C: An iterative algorithm for approximating convex minimization problem. Applied Mathematics and Computation 2007,188(1):648–656. 10.1016/j.amc.2006.10.039
Yao Y, Chen R, Yao J-C: Strong convergence and certain control conditions for modified Mann iteration. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1687–1693. 10.1016/j.na.2007.01.009
Ding XP: Perturbed Ishikawa type iterative algorithm for generalized quasivariational inclusions. Applied Mathematics and Computation 2003,141(2–3):359–373. 10.1016/S0096-3003(02)00261-8
Huang N-J: Mann and Ishikawa type perturbed iterative algorithms for generalized nonlinear implicit quasi-variational inclusions. Computers & Mathematics with Applications 1998,35(10):1–7. 10.1016/S0898-1221(98)00066-2
Fang Y-P, Huang N-J:
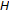 -monotone operator and resolvent operator technique for variational inclusions. Applied Mathematics and Computation 2003,145(2–3):795–803. 10.1016/S0096-3003(03)00275-3
-monotone operator and resolvent operator technique for variational inclusions. Applied Mathematics and Computation 2003,145(2–3):795–803. 10.1016/S0096-3003(03)00275-3Lin L-J: Variational inclusions problems with applications to Ekeland's variational principle, fixed point and optimization problems. Journal of Global Optimization 2007,39(4):509–527. 10.1007/s10898-007-9153-1
Verma RU: General system of
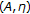 -monotone variational inclusion problems based on generalized hybrid iterative algorithm. Nonlinear Analysis: Hybrid Systems 2007,1(3):326–335. 10.1016/j.nahs.2006.07.002
-monotone variational inclusion problems based on generalized hybrid iterative algorithm. Nonlinear Analysis: Hybrid Systems 2007,1(3):326–335. 10.1016/j.nahs.2006.07.002Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Acknowledgment
The author was supported in part by NSC 98-2622-E-230-006-CC3 and NSC 98-2923-E-110-003-MY3.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liou, YC. An Iterative Algorithm for Mixed Equilibrium Problems and Variational Inclusions Approach to Variational Inequalities. Fixed Point Theory Appl 2010, 564361 (2010). https://doi.org/10.1155/2010/564361
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/564361
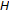 -monotone operator and resolvent operator technique for variational inclusions. Applied Mathematics and Computation 2003,145(2–3):795–803. 10.1016/S0096-3003(03)00275-3
-monotone operator and resolvent operator technique for variational inclusions. Applied Mathematics and Computation 2003,145(2–3):795–803. 10.1016/S0096-3003(03)00275-3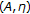 -monotone variational inclusion problems based on generalized hybrid iterative algorithm. Nonlinear Analysis: Hybrid Systems 2007,1(3):326–335. 10.1016/j.nahs.2006.07.002
-monotone variational inclusion problems based on generalized hybrid iterative algorithm. Nonlinear Analysis: Hybrid Systems 2007,1(3):326–335. 10.1016/j.nahs.2006.07.002