- Research Article
- Open access
- Published:
Halpern's Iteration in CAT(0) Spaces
Fixed Point Theory and Applications volume 2010, Article number: 471781 (2009)
Abstract
Motivated by Halpern's result, we prove strong convergence theorem of an iterative sequence in CAT(0) spaces. We apply our result to find a common fixed point of a family of nonexpansive mappings. A convergence theorem for nonself mappings is also discussed.
1. Introduction
Let  be a metric space and
be a metric space and  with
with  . A geodesic path from
. A geodesic path from  to
to  is an isometry
is an isometry  such that
such that  and
and  . The image of a geodesic path is called a geodesic segment. A metric space
. The image of a geodesic path is called a geodesic segment. A metric space  is a (uniquely) geodesic space if every two points of
is a (uniquely) geodesic space if every two points of  are joined by only one geodesic segment. A geodesic triangle
are joined by only one geodesic segment. A geodesic triangle in a geodesic space
in a geodesic space  consists of three points
consists of three points  of
of  and three geodesic segments joining each pair of vertices. A comparison triangle of a geodesic triangle
and three geodesic segments joining each pair of vertices. A comparison triangle of a geodesic triangle  is the triangle
is the triangle  in the Euclidean space
in the Euclidean space  such that
such that  for all
for all  .
.
A geodesic space  is a CAT(0) space if for each geodesic triangle
is a CAT(0) space if for each geodesic triangle  in
in  and its comparison triangle
and its comparison triangle  in
in  , the CAT(0) inequality
, the CAT(0) inequality

is satisfied by all  and
and  . The meaning of the CAT(0) inequality is that a geodesic triangle in
. The meaning of the CAT(0) inequality is that a geodesic triangle in  is at least thin as its comparison triangle in the Euclidean plane. A thorough discussion of these spaces and their important role in various branches of mathematics are given in [1, 2]. The complex Hilbert ball with the hyperbolic metric is an example of a CAT(0) space (see [3]).
is at least thin as its comparison triangle in the Euclidean plane. A thorough discussion of these spaces and their important role in various branches of mathematics are given in [1, 2]. The complex Hilbert ball with the hyperbolic metric is an example of a CAT(0) space (see [3]).
The concept of  -convergence introduced by Lim in 1976 was shown by Kirk and Panyanak [4] in CAT(0) spaces to be very similar to the weak convergence in Banach space setting. Several convergence theorems for finding a fixed point of a nonexpansive mapping have been established with respect to this type of convergence (e.g., see [5–7]). The purpose of this paper is to prove strong convergence of iterative schemes introduced by Halpern [8] in CAT(0) spaces. Our results are proved under weaker assumptions as were the case in previous papers and we do not use
-convergence introduced by Lim in 1976 was shown by Kirk and Panyanak [4] in CAT(0) spaces to be very similar to the weak convergence in Banach space setting. Several convergence theorems for finding a fixed point of a nonexpansive mapping have been established with respect to this type of convergence (e.g., see [5–7]). The purpose of this paper is to prove strong convergence of iterative schemes introduced by Halpern [8] in CAT(0) spaces. Our results are proved under weaker assumptions as were the case in previous papers and we do not use  -convergence. We apply our result to find a common fixed point of a countable family of nonexpansive mappings. A convergence theorem for nonself mappings is also discussed.
-convergence. We apply our result to find a common fixed point of a countable family of nonexpansive mappings. A convergence theorem for nonself mappings is also discussed.
In this paper, we write  for the the unique point
for the the unique point  in the geodesic segment joining from
in the geodesic segment joining from  to
to  such that
such that

We also denote by  the geodesic segment joining from
the geodesic segment joining from  to
to  , that is,
, that is,  . A subset
. A subset  of a CAT(0) space is convex if
of a CAT(0) space is convex if  for all
for all  . For elementary facts about CAT(0) spaces, we refer the readers to [1] (or, briefly in [5]).
. For elementary facts about CAT(0) spaces, we refer the readers to [1] (or, briefly in [5]).
The following lemma plays an important role in our paper.
Lemma 1.1.
A geodesic space  is a CAT(0) space if and only if the following inequality
is a CAT(0) space if and only if the following inequality

is satisfied by all  and all
and all  . In particular, if
. In particular, if  are points in a CAT(0) space and
are points in a CAT(0) space and  , then
, then

Recall that a continuous linear functional  on
on  , the Banach space of bounded real sequences, is called a Banach limit if
, the Banach space of bounded real sequences, is called a Banach limit if  and
and  for all
for all  .
.
Lemma 1.2 (see [9, Proposition  ]).
]).
Let  be such that
be such that  for all Banach limits
for all Banach limits  and
and  . Then
. Then  .
.
Lemma 1.3 (see [10, Lemma  ]).
]).
Let  be a sequence of nonnegative real numbers,
be a sequence of nonnegative real numbers,  a sequence of real numbers in
a sequence of real numbers in  with
with  ,
,  a sequence of nonnegative real numbers with
a sequence of nonnegative real numbers with  , and
, and  a sequence of real numbers with
a sequence of real numbers with  . Suppose that
. Suppose that

Then  .
.
2. Halpern's Iteration for a Single Mapping
Lemma 2.1.
Let  be a closed convex subset of a complete CAT(0) space
be a closed convex subset of a complete CAT(0) space  and let
and let  be a nonexpansive mapping. Let
be a nonexpansive mapping. Let  be fixed. For each
be fixed. For each  , the mapping
, the mapping  defined by
defined by

has a unique fixed point  , that is,
, that is,

Proof.
For  , we consider the triangle
, we consider the triangle  and its comparison triangle and we have the following:
and its comparison triangle and we have the following:

This implies that  is a contraction mapping and hence the conclusion follows.
is a contraction mapping and hence the conclusion follows.
The following result is proved by Kirk in [11, Theorem  ] under the boundedness assumption on
] under the boundedness assumption on  . We present here a new proof which is modified from Kirk's proof.
. We present here a new proof which is modified from Kirk's proof.
Lemma 2.2.
Let  ,
,  be as the preceding lemma. Then
be as the preceding lemma. Then  if and only if
if and only if  given by the formula (2.2) remains bounded as
given by the formula (2.2) remains bounded as  . In this case, the following statements hold:
. In this case, the following statements hold:
(1) converges to the unique fixed point
converges to the unique fixed point  of
of  which is nearest
which is nearest  ;
;
(2) for all Banach limits
for all Banach limits  and all bounded sequences
and all bounded sequences  with
with  .
.
Proof.
If  , then it is clear that
, then it is clear that  is bounded. Conversely, suppose that
is bounded. Conversely, suppose that  is bounded. Let
is bounded. Let  be any sequence in
be any sequence in  such that
such that  and define
and define  by
by

for all  . By the boundedness of
. By the boundedness of  , we have
, we have  . We choose a sequence
. We choose a sequence  in
in  such that
such that  . It follows from Lemma 1.1 that
. It follows from Lemma 1.1 that

Then, by the convexity of  ,
,

This implies that  is a Cauchy sequence in
is a Cauchy sequence in  and hence it converges to a point
and hence it converges to a point  . Suppose that
. Suppose that  is a point in
is a point in  satisfying
satisfying  . It follows then that
. It follows then that

and hence  . Moreover,
. Moreover,  is a fixed point of
is a fixed point of  . To see this, we consider
. To see this, we consider

and

This implies that  and hence
and hence  .
.
-
(1)
is proved in [12, Theorem
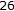 ]. In fact, it is shown that
]. In fact, it is shown that  is the nearest point of
is the nearest point of  to
to  . Finally, we prove (2). Suppose that
. Finally, we prove (2). Suppose that  is a sequence given by the formula (2.2), where
is a sequence given by the formula (2.2), where 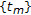 is a sequence in
is a sequence in 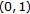 such that
such that  . We also assume that
. We also assume that  is the nearest point of
is the nearest point of 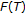 to
to  . By the first inequality in Lemma 1.1, we have
. By the first inequality in Lemma 1.1, we have

Let  be a Banach limit. Then
be a Banach limit. Then

This implies that

Letting  gives
gives

In particular,

Inspired by the results of Wittmann [13] and of Shioji and Takahashi [9], we use the iterative scheme introduced by Halpern to obtain a strong convergence theorem for a nonexpansive mapping in CAT(0) space setting. A part of the following theorem is proved in [14].
Theorem 2.3.
Let  be a closed convex subset of a complete CAT(0) space
be a closed convex subset of a complete CAT(0) space  and let
and let  be a nonexpansive mapping with a nonempty fixed point set
be a nonexpansive mapping with a nonempty fixed point set  . Suppose that
. Suppose that  are arbitrarily chosen and
are arbitrarily chosen and  is iteratively generated by
is iteratively generated by

where  is a sequence in
is a sequence in  satisfying
satisfying
(C1) ;
;
(C2) ;
;
(C3) or
or  .
.
Then  converges to
converges to  which is the nearest point of
which is the nearest point of  to
to  .
.
Proof.
We first show that the sequence  is bounded. Let
is bounded. Let  . Then
. Then

By induction, we have

for all  . This implies that
. This implies that  is bounded and so is the sequence
is bounded and so is the sequence  .
.
Next, we show that  . To see this, we consider the following:
. To see this, we consider the following:

By the conditions (C2) and (C3), we have

Consequently, by the condition (C1),

From Lemma 2.2, let  where
where  is given by the formula (2.2). Then
is given by the formula (2.2). Then  is the nearest point of
is the nearest point of  to
to  . We next consider the following:
. We next consider the following:

By Lemma 2.2, we have  for all Banach limits
for all Banach limits  . Moreover, since
. Moreover, since  ,
,

It follows from  and Lemma 1.2 that
and Lemma 1.2 that

Hence the conclusion follows by Lemma 1.3.
3. Halpern's Iteration for a Family of Mappings
3.1. Finitely Many Mappings
We use the "cyclic method" [15] and Bauschke's condition [16] to obtain the following strong convergence theorem for a finite family of nonexpansive mappings.
Theorem 3.1.
Let  be a complete CAT(0) space and
be a complete CAT(0) space and  a closed convex subset of
a closed convex subset of  . Let
. Let  be nonexpansive mappings with
be nonexpansive mappings with  and let
and let  be arbitrarily chosen. Define an iterative sequence
be arbitrarily chosen. Define an iterative sequence  by
by

where  is a sequence in
is a sequence in  satisfying
satisfying
(C1) ;
;
(C2) ;
;
(C3) or
or  .
.
Suppose, in addition, that

Then  converges to
converges to  which is nearest
which is nearest  .
.
Here the  function takes values in
function takes values in  .
.
Proof.
By [16, Theorem  ], we have
], we have

The proof line now follows from the proofs of Theorem 2.3 and [15, Theorem  ].
].
3.2. Countable Mappings
The following concept is introduced by Aoyama et al. [10]. Let  be a complete CAT(0) space and
be a complete CAT(0) space and  a subset of
a subset of  . Let
. Let  be a countable family of mappings from
be a countable family of mappings from  into itself. We say that a family
into itself. We say that a family  satisfies AKTT-condition if
satisfies AKTT-condition if

for each bounded subset of  of
of  .
.
If  is a closed subset and
is a closed subset and  satisfies AKTT-condition, then we can define
satisfies AKTT-condition, then we can define  such that
such that

In this case, we also say that  satisfies AKTT-condition.
satisfies AKTT-condition.
Theorem 3.2.
Let  be a complete CAT(0) space and
be a complete CAT(0) space and  a closed convex subset of
a closed convex subset of  . Let
. Let  be a countable family of nonexpansive mappings with
be a countable family of nonexpansive mappings with  . Suppose that
. Suppose that  are arbitrarily chosen and
are arbitrarily chosen and  is defined by
is defined by

where  is a sequence in
is a sequence in  satisfying
satisfying
(C1) ;
;
(C2) ;
;
(C3) or
or  .
.
Suppose, in addition, that
(M1) satisfies AKTT-condition;
satisfies AKTT-condition;
(M2) .
.
Then  converges to
converges to  which is nearest
which is nearest  .
.
Proof.
Since the proof of this theorem is very similar to that of Theorem 2.3, we present here only the sketch proof. First, we notice that both sequences  and
and  are bounded and
are bounded and

By conditions (C2), (C3), AKTT-condition, and Lemma 1.3, we have

Consequently,  and hence
and hence

Let  be the nearest point of
be the nearest point of  to
to  . As in the proof of Theorem 2.3, we have
. As in the proof of Theorem 2.3, we have  for all Banach limits
for all Banach limits  and
and  . We observe that
. We observe that

and this implies that

Therefore,  and hence
and hence  converges to
converges to  .
.
We next show how to generate a family of mappings from a given family of mappings to satisfy conditions (M1) and (M2) of the preceding theorem. The following is an analogue of Bruck's result [17] in CAT(0) space setting. The idea using here is from [10].
Theorem 3.3.
Let  be a complete CAT(0) space and
be a complete CAT(0) space and  a closed convex subset of
a closed convex subset of  . Suppose that
. Suppose that  is a countable family of nonexpansive mappings with
is a countable family of nonexpansive mappings with  . Then there exist a family of nonexpansive mappings
. Then there exist a family of nonexpansive mappings  and a nonexpansive mapping
and a nonexpansive mapping  such that
such that
(M1) satisfies AKTT-condition;
satisfies AKTT-condition;
(M2) .
.
Lemma 3.4.
Let  and
and  be as above. Suppose that
be as above. Suppose that  are nonexpansive mappings and
are nonexpansive mappings and  . Then, for any
. Then, for any  , the mapping
, the mapping  is nonexpansive and
is nonexpansive and  .
.
Proof.
To see that  is nonexpansive, we only apply the triangle inequality and two applications of the second inequality in Lemma 1.1. We next prove the latter. It is clear that
is nonexpansive, we only apply the triangle inequality and two applications of the second inequality in Lemma 1.1. We next prove the latter. It is clear that  . To see the reverse inclusion, let
. To see the reverse inclusion, let  and
and  . Then, by the first inequality of Lemma 1.1,
. Then, by the first inequality of Lemma 1.1,

This implies  . As
. As  , we have
, we have  , as desired.
, as desired.
Proof of Theorem 3.3.
We first define a family of mappings  by
by

By Lemma 3.4, each  is a nonexpansive mapping satisfying
is a nonexpansive mapping satisfying  . Notice that, for fixed
. Notice that, for fixed  ,
,

From the estimation above, we have

for each bounded subset  of
of  . In particular,
. In particular,  is a Cauchy sequence for each
is a Cauchy sequence for each  . We now define the nonexpansive mapping
. We now define the nonexpansive mapping  by
by

Finally, we prove that

The latter equality is clearly verified and  holds. On the other hand, let
holds. On the other hand, let  and
and  . We consider the following:
. We consider the following:

Then

Letting  yields
yields

Because  , we have
, we have  . Continuing this procedure we obtain that
. Continuing this procedure we obtain that  and hence
and hence  . This completes the proof.
. This completes the proof.
4. Nonself Mappings
From Bridson and Haefliger's book (page 176), the following result is proved.
Theorem 4.1.
Let  be a complete CAT(0) space and
be a complete CAT(0) space and  a closed convex subset of
a closed convex subset of  . Then the followings hold true.
. Then the followings hold true.
(i)For each  , there exists an element
, there exists an element  such that
such that

(ii) for all
for all  .
.
(iii)The mapping  is nonexpansive.
is nonexpansive.
The mapping  in the preceding theorem is called the metric projection from
in the preceding theorem is called the metric projection from onto
onto . From this, we have the following result.
. From this, we have the following result.
Theorem 4.2.
Let  be a complete CAT(0) space and
be a complete CAT(0) space and  a closed convex subset of
a closed convex subset of  . Let
. Let  be a nonself nonexpansive mapping with
be a nonself nonexpansive mapping with  and
and  the metric projection from
the metric projection from  onto
onto  . Then the mapping
. Then the mapping  is nonexpansive and
is nonexpansive and  .
.
Proof.
It follows from Theorem 4.1 that  is nonexpansive. To see the latter, it suffices to show that
is nonexpansive. To see the latter, it suffices to show that  . Let
. Let  and
and  . Since
. Since

we have  and this finishes the proof.
and this finishes the proof.
By the preceding theorem and Theorem 2.3, we obtain the following result.
Theorem 4.3.
Let  ,
,  ,
,  , and
, and  be as the same as Theorem 4.2. Suppose that
be as the same as Theorem 4.2. Suppose that  are arbitrarily chosen and the sequence
are arbitrarily chosen and the sequence  is defined by
is defined by

where  is a sequence in
is a sequence in  satisfying
satisfying
(C1) ;
;
(C2) ;
;
(C3) or
or  .
.
Then  converges to
converges to  which is nearest
which is nearest  .
.
References
Bridson MR, Haefliger A: Metric Spaces of Non-Positive Curvature, Grundlehren der Mathematischen Wissenschaften. Volume 319. Springer, Berlin, Germany; 1999:xxii+643.
Burago D, Burago Y, Ivanov S: A Course in Metric Geometry, Graduate Studies in Mathematics. Volume 33. American Mathematical Society, Providence, RI, USA; 2001:xiv+415.
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Monographs and Textbooks in Pure and Applied Mathematics. Volume 83. Marcel Dekker, New York, NY, USA; 1984:ix+170.
Kirk WA, Panyanak B: A concept of convergence in geodesic spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,68(12):3689–3696. 10.1016/j.na.2007.04.011
Dhompongsa S, Panyanak B: On -convergence theorems in CAT(0) spaces. Computers & Mathematics with Applications 2008,56(10):2572–2579. 10.1016/j.camwa.2008.05.036
Dhompongsa S, Fupinwong W, Kaewkhao A: Common fixed points of a nonexpansive semigroup and a convergence theorem for Mann iterations in geodesic metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(12):4268–4273. 10.1016/j.na.2008.09.012
Laokul T, Panyanak B: Approximating fixed points of nonexpansive mappings in CAT(0) spaces. International Journal of Mathematical Analysis 2009, 3: 1305–1315.
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Shioji N, Takahashi W: Strong convergence of approximated sequences for nonexpansive mappings in Banach spaces. Proceedings of the American Mathematical Society 1997,125(12):3641–3645. 10.1090/S0002-9939-97-04033-1
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007,67(8):2350–2360. 10.1016/j.na.2006.08.032
Kirk WA: Geodesic geometry and fixed point theory. In Seminar of Mathematical Analysis (Malaga/Seville, 2002/2003), Colección Abierta. Volume 64. University of Sevilla Secretary, Seville, Spain; 2003:195–225.
Kirk WA: Fixed point theorems in CAT(0) spaces and -trees. Fixed Point Theory and Applications 2004,2004(4):309–316.
Wittmann R: Approximation of fixed points of nonexpansive mappings. Archiv der Mathematik 1992,58(5):486–491. 10.1007/BF01190119
Aoyama K, Eshita K, Takahashi W: Iteration processes for nonexpansive mappings in convex metric spaces. In Nonlinear Analysis and Convex Analysis. Yokohama, Yokohama, Japan; 2007:31–39.
Bauschke HH: The approximation of fixed points of compositions of nonexpansive mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1996,202(1):150–159. 10.1006/jmaa.1996.0308
Suzuki T: Some notes on Bauschke's condition. Nonlinear Analysis: Theory, Methods & Applications 2007,67(7):2224–2231. 10.1016/j.na.2006.09.014
Bruck RE Jr.: Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Transactions of the American Mathematical Society 1973, 179: 251–262.
Acknowledgments
The author would like to thank the referee for the information that a part of Theorem 2.3 was proved in [14]. This work was supported by the Centre of Excellence in Mathematics, the Commission on Higher Education, Thailand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saejung, S. Halpern's Iteration in CAT(0) Spaces. Fixed Point Theory Appl 2010, 471781 (2009). https://doi.org/10.1155/2010/471781
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/471781
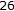 ]. In fact, it is shown that
]. In fact, it is shown that  is the nearest point of
is the nearest point of  to
to  . Finally, we prove (2). Suppose that
. Finally, we prove (2). Suppose that  is a sequence given by the formula (2.2), where
is a sequence given by the formula (2.2), where 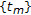 is a sequence in
is a sequence in 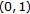 such that
such that  . We also assume that
. We also assume that  is the nearest point of
is the nearest point of 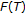 to
to  . By the first inequality in Lemma 1.1, we have
. By the first inequality in Lemma 1.1, we have