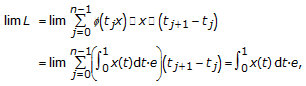- Research Article
- Open access
- Published:
A Counterexample on a Theorem by Khojasteh, Goodarzi, and Razani
Fixed Point Theory and Applications volume 2010, Article number: 470141 (2010)
Abstract
In the paper by Khojasteh et al. (2010), the authors tried to generalize Branciari's theorem, introducing the new integral type contraction mappings. In this note we give a counterexample on their main statement (Theorem 2.9). Also we give a comment explaining what the mistake in the proof is, and suggesting what conditions might be appropriate in generalizing fixed point results to cone spaces, where the cone is taken from the infinite dimensional space.
1. Introduction
In the paper [1], Branciari proved the following fixed point theorem with integral-type contraction condition.
Theorem 1.1.
Let  be a complete metric space,
be a complete metric space,  , and
, and  is a mapping such that for all
is a mapping such that for all  ,
,

where  is nonnegative measurable mapping, having finite integral on each compact subset of
is nonnegative measurable mapping, having finite integral on each compact subset of  such that for each
such that for each  ,
,  . Then
. Then  has a unique fixed point
has a unique fixed point  , such that for each
, such that for each  ,
,  .
.
There are many generalizations of fixed point results to the so-called cone metric spaces, introduced by several Russian authors in mid-20th. These spaces are re-introduced by Huang and Zhang [2]. In the same paper, the notion of convergent and Cauchy sequences are given.
Definition 1.2.
Let  be a Banach space. By
be a Banach space. By  we denote the zero element of
we denote the zero element of  . A subset
. A subset  of
of  is called a cone if
is called a cone if
(1) is closed, nonempty, and
is closed, nonempty, and  ;
;
(2) ,
,  , and
, and  imply
imply  ;
;
(3) .
.
Given a cone  , we define partial ordering
, we define partial ordering  on
on  with respect to
with respect to  by
by  if and only if
if and only if  . We will write
. We will write  to indicate that
to indicate that  and
and  , whereas
, whereas  will stand for
will stand for  (interior of
(interior of  ).
).
We say that  is a solid cone if and only if
is a solid cone if and only if  .
.
Let  be a solid cone in
be a solid cone in  and let
and let  be the corresponding partial ordering on
be the corresponding partial ordering on  with respect to
with respect to  . We say that
. We say that  is a normal cone if and only if there exists a real number
is a normal cone if and only if there exists a real number  such that
such that  implies
implies

for each  . The least positive
. The least positive  satisfying (1.2) is called the normal constant of
satisfying (1.2) is called the normal constant of  .
.
Definition 1.3.
Let  be a nonempty set. Suppose that a mapping
be a nonempty set. Suppose that a mapping  satisfies:
satisfies:
(1) for all
for all  and
and  if and only if
if and only if  ;
;
(2) for all
for all  ;
;
(3) for all
for all  .
.
Then,  is called a cone metric on
is called a cone metric on  , and
, and  is called a cone metric space.
is called a cone metric space.
Definition 1.4.
Let  be a solid cone metric space, let
be a solid cone metric space, let  , and let
, and let  be a sequence in
be a sequence in  . Then
. Then
(1) converges to
converges to  if for every
if for every  there exists a positive integer
there exists a positive integer  such that for all
such that for all 
 . We denote this by
. We denote this by  or
or  ;
;
(2) is a cone Cauchy sequences if for every
is a cone Cauchy sequences if for every  there exists a positive integer
there exists a positive integer  such that for all
such that for all 
 ;
;
(3) is a complete cone metric space if every Cauchy sequence is convergent.
is a complete cone metric space if every Cauchy sequence is convergent.
In the paper [3] Khojasteh et al. tried to generalize Branciari fixed point result to the cone metric spaces. They introduce the concept of integration along the interval  as a limit of Cauchy sums.
as a limit of Cauchy sums.
Definition 1.5 (see [3]).
Let  be a normal solid cone, and let
be a normal solid cone, and let  . We say that
. We say that  is integrable on
is integrable on  if and only if the following sums:
if and only if the following sums:

converge to the same element of  , where
, where  form a partition of
form a partition of  . Clearly,
. Clearly,  stands for
stands for  . This element is denoted by
. This element is denoted by

We say that  is subadditive if and only if for any
is subadditive if and only if for any  there holds
there holds

Using this concept, they stated the following statement (Theorem  in [3]).
in [3]).
Theorem 1.6 (see [3]).
Let  be a complete cone metric space and let
be a complete cone metric space and let  be a normal cone. Suppose that
be a normal cone. Suppose that  is a nonvanishing map which is subadditive cone integrable on each
is a nonvanishing map which is subadditive cone integrable on each  and such that for each
and such that for each  ,
,  . If
. If  is a map such that for all
is a map such that for all  ,
,

for some  , then
, then  has a unique fixed point in
has a unique fixed point in  .
.
However, the last statement is not true. This will be proved in the next section.
2. Constructing the Counterexample
Consider the Banach space

with the norm  , and the cone
, and the cone

It is obvious that  is a normal solid cone with normal constant equals to
is a normal solid cone with normal constant equals to  .
.
Consider the set

and the mapping  given by
given by

Proposition 2.1.
(a)
-
(b)
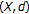 is a cone metric space.
is a cone metric space. -
(c)
A sequence
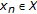 is convergent (in
is convergent (in 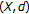 ) to
) to  if and only if
if and only if 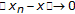 . Also
. Also 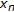 is Cauchy sequence (in
is Cauchy sequence (in 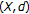 ) if and only if
) if and only if 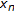 is a Cauchy sequence with respect to norm in
is a Cauchy sequence with respect to norm in 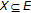 .
. -
(d)
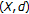 is a complete cone metric space.
is a complete cone metric space.
Proof.
-
(a)
and (b) obvious.
-
(c)
Let
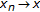 (in
(in 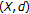 ), and let
), and let 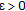 . Then, the function
. Then, the function  , and we have that for all
, and we have that for all 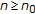 and for all
and for all 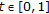 there holds
there holds 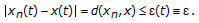 (2.5)
(2.5)
Let  , and let
, and let  . Then there exists
. Then there exists  such that for all
such that for all  ,
,  . Also for all
. Also for all  there holds
there holds

Hence,  implying
implying  .
.
The similar argument proves the second part of the statement concerning Cauchy sequences.
-
(d)
The set
 can be represented as
can be represented as 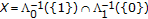 , where
, where  is the bounded linear functional given by
is the bounded linear functional given by 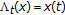 . Therefore,
. Therefore, 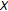 is a closed subset of
is a closed subset of 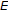 and hence complete in the norm. By part (c) of this proposition, it implies that
and hence complete in the norm. By part (c) of this proposition, it implies that 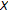 is a complete cone metric space.
is a complete cone metric space.
Let  denote the function identically equal to
denote the function identically equal to  . Consider the mapping
. Consider the mapping  given by
given by

for  and
and  .
.
Proposition 2.2.
(a) is integrable on every segment
is integrable on every segment  and
and  .
.
(b) is a nonvanishing subadditive function such that for all
is a nonvanishing subadditive function such that for all  there holds
there holds  .
.
Proof.
-
(a)
The integrability of
 on
on 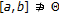 follows immediately from its continuity. Further, let
follows immediately from its continuity. Further, let 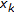 be a partition of
be a partition of 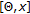 . Then
. Then  for some partition
for some partition  of
of 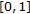 , and we have
, and we have 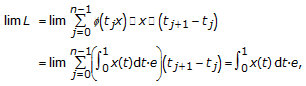 (2.8)
(2.8)
and similarly  .
.
-
(b)
Follows from the part (a).
Proposition 2.3.
Let the space  be defined by (2.1) and (2.3). Let
be defined by (2.1) and (2.3). Let  be given by
be given by  for
for  , and
, and  , otherwise, and let
, otherwise, and let  .
.
The space  together with the mappings
together with the mappings  and
and  satisfies all assumptions of Theorem 1.6. On the other hand,
satisfies all assumptions of Theorem 1.6. On the other hand,  has no fixed point.
has no fixed point.
Proof.
We only have to check the inequality (1.6). Note that for all  and all
and all  we have
we have  . Also, note that
. Also, note that  is a linear mapping, and
is a linear mapping, and  . Therefore
. Therefore  . Thus (1.6) becomes
. Thus (1.6) becomes

Taking into account Proposition 2.2, part (a), we have for all 

Putting  , we obtain
, we obtain

which completes the proof of the first statement.
On the other hand,  has no fixed point. Namely, if we suppose that
has no fixed point. Namely, if we suppose that  is a fixed point for
is a fixed point for  , it means that
, it means that  for all
for all  , and moreover
, and moreover  for all
for all  , and also for all
, and also for all  , by induction. By continuity of
, by induction. By continuity of  , it follows that
, it follows that  implying
implying  !
!
3. A Comment
The mistake in the proof of Theorem 1.6 given in [3] is in the following. The authors from  conclude that
conclude that  also, which is unjustifiable. The original Branciari's proof [1] deals with one-dimensional integral, and such conclusion is valid due to the implication
also, which is unjustifiable. The original Branciari's proof [1] deals with one-dimensional integral, and such conclusion is valid due to the implication

and the existence of the total ordering on  . However, in infinite dimensional case, such conclusion invokes continuity of the function inverse to
. However, in infinite dimensional case, such conclusion invokes continuity of the function inverse to  . Even for the linear mappings this is not always true, but only under additional assumption that initial mapping is bijective. This asserts the well known Banach open mapping theorem. In the absence of some generalization of the open mapping theorem to nonlinear case, it is necessary to include continuity of the inverse function in the assumptions, as it was done in [4].
. Even for the linear mappings this is not always true, but only under additional assumption that initial mapping is bijective. This asserts the well known Banach open mapping theorem. In the absence of some generalization of the open mapping theorem to nonlinear case, it is necessary to include continuity of the inverse function in the assumptions, as it was done in [4].
References
Branciari A: A fixed point theorem for mappings satisfying a general contractive condition of integral type. International Journal of Mathematics and Mathematical Sciences 2002,29(9):531–536. 10.1155/S0161171202007524
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Khojasteh F, Goodarzi Z, Razani A: Some fixed point theorems of integral type contraction in cone metric spaces. Fixed Point Theory and Applications 2010, Article ID 189684 2010:-13.
Sabetghadam F, Masiha HP: Common fixed points for generalized -pair mappings on cone metric spaces. Fixed Point Theory and Applications 2010, Article ID 718340 2010:-8.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Arandelović, I., Kečkić, D. A Counterexample on a Theorem by Khojasteh, Goodarzi, and Razani. Fixed Point Theory Appl 2010, 470141 (2010). https://doi.org/10.1155/2010/470141
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/470141
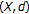 is a cone metric space.
is a cone metric space.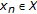 is convergent (in
is convergent (in 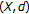 ) to
) to  if and only if
if and only if 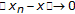 . Also
. Also 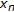 is Cauchy sequence (in
is Cauchy sequence (in 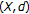 ) if and only if
) if and only if 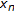 is a Cauchy sequence with respect to norm in
is a Cauchy sequence with respect to norm in 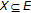 .
.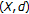 is a complete cone metric space.
is a complete cone metric space.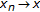 (in
(in 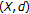 ), and let
), and let 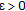 . Then, the function
. Then, the function  , and we have that for all
, and we have that for all 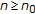 and for all
and for all 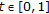 there holds
there holds 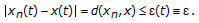
 can be represented as
can be represented as 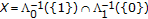 , where
, where  is the bounded linear functional given by
is the bounded linear functional given by 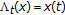 . Therefore,
. Therefore, 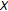 is a closed subset of
is a closed subset of 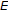 and hence complete in the norm. By part (c) of this proposition, it implies that
and hence complete in the norm. By part (c) of this proposition, it implies that 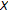 is a complete cone metric space.
is a complete cone metric space. on
on 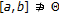 follows immediately from its continuity. Further, let
follows immediately from its continuity. Further, let 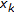 be a partition of
be a partition of 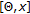 . Then
. Then  for some partition
for some partition  of
of 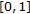 , and we have
, and we have