- Research Article
- Open access
- Published:
Fixed Point Theorems for Suzuki Generalized Nonexpansive Multivalued Mappings in Banach Spaces
Fixed Point Theory and Applications volume 2010, Article number: 457935 (2010)
Abstract
In the first part of this paper, we prove the existence of common fixed points for a commuting pair consisting of a single-valued and a multivalued mapping both satisfying the Suzuki condition in a uniformly convex Banach space. In this way, we generalize the result of Dhompongsa et al. (2006). In the second part of this paper, we prove a fixed point theorem for upper semicontinuous mappings satisfying the Suzuki condition in strictly  spaces; our result generalizes a recent result of Domínguez-Benavides et al. (2009).
spaces; our result generalizes a recent result of Domínguez-Benavides et al. (2009).
1. Introduction
A mapping  on a subset
on a subset  of a Banach space
of a Banach space  is said to be nonexpansive if
is said to be nonexpansive if

In 2008, Suzuki [1] introduced a condition which is weaker than nonexpansiveness. Suzuki's condition which was named by him the condition  reads as follows: a mapping
reads as follows: a mapping  is said to satisfy the condition
is said to satisfy the condition  on
on  if
if

He then proved some fixed point and convergence theorems for such mappings. We shall at times refer to this concept by saying that  is a generalized nonexpansive mapping in the sense of Suzuki. Very recently, the current authors used a modified Suzuki condition for multivalued mappings and proved a fixed point theorem for multivalued mappings satisfying this condition in uniformly convex Banach spaces (see [2]).
is a generalized nonexpansive mapping in the sense of Suzuki. Very recently, the current authors used a modified Suzuki condition for multivalued mappings and proved a fixed point theorem for multivalued mappings satisfying this condition in uniformly convex Banach spaces (see [2]).
In this paper, we first present a common fixed point theorem for commuting pairs consisting of a single-valued and a multivalued mapping both satisfying the Suzuki condition. This result extends a result of Dhompongsa et al. [3].
In the next part, we shall consider a recent result of Domínguez-Benavides et al. [4] on the existence of fixed points in an important class of spaces which are usually called strictly  spaces. These spaces contain all Lebesgue function spaces
spaces. These spaces contain all Lebesgue function spaces  for
for  . In this paper, we also generalize results of Domínguez-Benavides et al. [4] to upper semicontinuous mappings satisfying the Suzuki condition.
. In this paper, we also generalize results of Domínguez-Benavides et al. [4] to upper semicontinuous mappings satisfying the Suzuki condition.
2. Preliminaries
Given a mapping  on a subset
on a subset  of a Banach space
of a Banach space  , the set of its fixed points will be denoted by
, the set of its fixed points will be denoted by

We start by the following definition due to Suzuki.
Definition 2.1 (see [1]).
Let  be a mapping on a subset
be a mapping on a subset  of a Banach space
of a Banach space  . The mapping
. The mapping  is said to satisfy the Suzuki condition
is said to satisfy the Suzuki condition  if
if

As the following example shows, the Suzuki condition is weaker than nonexpansiveness. Therefore, it is natural to call these mappings as "generalized nonexpansive mappings". However, we shall at times refer to these mappings as those satisfying the condition  .
.
Example 2.2.
Let  be equipped with the usual metric
be equipped with the usual metric  , and let
, and let  . We put
. We put

The mapping  is continuous and satisfies the condition
is continuous and satisfies the condition  . However,
. However,  is not nonexpansive.
is not nonexpansive.
Lemma 2.3 (see [1, Lemma  ]).
]).
Let  be a mapping defined on a closed subset
be a mapping defined on a closed subset  of a Banach space
of a Banach space  . Assume that
. Assume that  satisfies the condition
satisfies the condition  . Then
. Then  is closed. Moreover, if
is closed. Moreover, if  is strictly convex and
is strictly convex and  is convex, then
is convex, then  is also convex.
is also convex.
Theorem 2.4 (see [5, Theorem  ]).
]).
Let  be a nonempty bounded closed convex subset of a uniformly convex Banach space
be a nonempty bounded closed convex subset of a uniformly convex Banach space  . Let
. Let  be a mapping satisfying the condition (
be a mapping satisfying the condition ( ). Then
). Then  has a fixed point.
has a fixed point.
Let  be a metric space. We denote by
be a metric space. We denote by  the collection of all nonempty closed bounded subsets of
the collection of all nonempty closed bounded subsets of  ; we also write
; we also write  to denote the collection of all nonempty compact convex subsets of
to denote the collection of all nonempty compact convex subsets of  . Let
. Let  be the Hausdorff metric with respect to
be the Hausdorff metric with respect to  , that is,
, that is,

for all  where
where 
Let  be a multivalued mapping. An element
be a multivalued mapping. An element  is said to be a fixed point of
is said to be a fixed point of  provided that
provided that 
Definition 2.5.
A multivalued mapping  is said to be nonexpansive provided that
is said to be nonexpansive provided that

Suzuki's condition can be modified to incorporate multivalued mappings. This was done by the current authors in [2]. We call these mappings generalized multivalued nonexpansive mappings in the sense of Suzuki or multivalued mappings satisfying the condition  . We now state Suzuki's condition for multivalued mappings as follows.
. We now state Suzuki's condition for multivalued mappings as follows.
Definition 2.6.
A multivalued mapping  is said to satisfy the condition
is said to satisfy the condition  provided that
provided that

Example 2.7.
Define a mapping  on
on  by
by

It is not difficult to see that  satisfies the Suzuki condition; however,
satisfies the Suzuki condition; however,  is not nonexpansive.
is not nonexpansive.
The following lemma, proved by Goebel and Kirk [6], plays an important role in the coming discussions.
Lemma 2.8.
Let  and
and  be two bounded sequences in a Banach space
be two bounded sequences in a Banach space  , and let
, and let  . If for every natural number
. If for every natural number  we have
we have  and
and  , then
, then  .
.
Definition 2.9.
A multivalued mapping  is said to be upper semicontinuous on
is said to be upper semicontinuous on  if
if  is open in
is open in  whenever
whenever  is open.
is open.
We recall that if  is single valued, then
is single valued, then  reduces to a continuous function.
reduces to a continuous function.
3. Fixed Points in Uniformly Convex Banach Spaces
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  . Assume that
. Assume that  is a bounded sequence in
is a bounded sequence in  . For each
. For each  , the asymptotic radius of
, the asymptotic radius of  at
at  is defined by
is defined by

Let

The number  is known as the asymptotic radius of
is known as the asymptotic radius of  relative to
relative to  . Similarly, the set
. Similarly, the set  is called the asymptotic center of
is called the asymptotic center of  relative to
relative to  . In the case that
. In the case that  is a reflexive Banach space and
is a reflexive Banach space and  is a nonempty closed convex bounded subset of
is a nonempty closed convex bounded subset of  , the set
, the set  is always a nonempty closed convex subset of
is always a nonempty closed convex subset of  . To see this, observe that by the definition of
. To see this, observe that by the definition of  , for each
, for each  , the set
, the set

is nonempty. It is not difficult to see that each  is closed and convex; hence
is closed and convex; hence

is closed and convex. Moreover, it follows from the weak compactness of  that
that  is nonempty. It is easy to see that if
is nonempty. It is easy to see that if  is uniformly convex and if
is uniformly convex and if  is a closed convex subset of
is a closed convex subset of  , then
, then  consists of exactly one point.
consists of exactly one point.
A bounded sequence  is said to be regular with respect to
is said to be regular with respect to  if for every subsequence
if for every subsequence  we have
we have

It is also known that if  is uniformly convex and if
is uniformly convex and if  is a nonempty closed convex subset of
is a nonempty closed convex subset of  , then for any
, then for any  , there exists a unique point
, there exists a unique point  such that
such that  .
.
The following lemma was proved by Goebel and Lim.
Let  be a bounded sequence in
be a bounded sequence in  and let
and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Then
. Then  has a subsequence which is regular relative to
has a subsequence which is regular relative to  .
.
Definition 3.2.
Let  be a nonempty closed convex bounded subset of a Banach space
be a nonempty closed convex bounded subset of a Banach space  , and let
, and let  and
and  be two mappings. Then
be two mappings. Then  and
and  are said to be commuting mappings if for every
are said to be commuting mappings if for every  such that
such that  and
and  , we have
, we have  .
.
Now the time is ripe to state and prove the main result of this section.
Theorem 3.3.
Let  be a nonempty closed convex bounded subset of a uniformly convex Banach space
be a nonempty closed convex bounded subset of a uniformly convex Banach space  . Let
. Let  be a single-valued mapping, and let
be a single-valued mapping, and let  be a multivalued mapping. If both
be a multivalued mapping. If both  and
and  satisfy the condition (
satisfy the condition ( ) and if
) and if  and
and  are commuting, then they have a common fixed point, that is, there exists a point
are commuting, then they have a common fixed point, that is, there exists a point  such that
such that  .
.
Proof.
By Theorem 2.4, the mapping  has a nonempty fixed point set
has a nonempty fixed point set  which is a closed convex subset of
which is a closed convex subset of  (by Lemma 2.3). We show that for
(by Lemma 2.3). We show that for  ,
,  . To see this, let
. To see this, let  ; since
; since  and
and  are commuting, we have
are commuting, we have  for each
for each  . Therefore,
. Therefore,  is invariant under
is invariant under  for each
for each  . Since
. Since  is a bounded closed convex subset of the uniformly convex Banach space
is a bounded closed convex subset of the uniformly convex Banach space  , we conclude that
, we conclude that  has a fixed point in
has a fixed point in  and therefore,
and therefore,  for
for 
Now we find an approximate fixed point sequence for  in
in  . Take
. Take  , since
, since  , therefore, we can choose
, therefore, we can choose  . Define
. Define

Since  is a convex set, we have
is a convex set, we have  . Let
. Let  be chosen in such a way that
be chosen in such a way that

We see that  Indeed, we have
Indeed, we have

Since  satisfies the condition
satisfies the condition  , we get
, we get

which contradicts the uniqueness of  as the unique nearest point of
as the unique nearest point of  (note that
(note that  ). Similarly, put
). Similarly, put  ; again we choose
; again we choose  in such a way that
in such a way that

By the same argument, we get  In this way, we will find a sequence
In this way, we will find a sequence  in
in  such that
such that  where
where  and
and

Therefore, for every natural number  we have
we have

from which it follows that

Our assumption now gives

hence

We now apply Lemma 2.8 to conclude that  where
where  . Moreover, by passing to a subsequence we may assume that
. Moreover, by passing to a subsequence we may assume that  is regular (see Lemma 3.1). Since
is regular (see Lemma 3.1). Since  is uniformly convex,
is uniformly convex,  is singleton, say
is singleton, say  (note that
(note that  . Let
. Let  . For each
. For each  , we choose
, we choose  such that
such that

On the other hand, there is a natural number  such that for every
such that for every  we have
we have  . This implies that
. This implies that

and hence from our assumption we obtain

Therefore,

Moreover,  for all natural numbers
for all natural numbers  Indeed, since
Indeed, since

we have

Since  and
and  , by the fact that the mappings
, by the fact that the mappings  and
and  are commuting, we obtain
are commuting, we obtain  . Now, by the uniqueness of
. Now, by the uniqueness of  as the nearest point to
as the nearest point to  , we get
, we get 
Since  is compact, the sequence
is compact, the sequence  has a convergent subsequence
has a convergent subsequence  with
with  . Because
. Because  for all
for all  , and
, and  is closed, we obtain
is closed, we obtain  . Note that
. Note that

and for  we have
we have  . This entails
. This entails

Since  is regular, this shows that
is regular, this shows that  . And hence
. And hence  .
.
As a consequence, we obtain the theorem already proved by Dhompongsa et al. (see [3, Theorem  ]).
]).
Corollary 3.4.
Let  be a nonempty closed convex bounded subset of a uniformly convex Banach space
be a nonempty closed convex bounded subset of a uniformly convex Banach space  ,
,  , and
, and  a single-valued and a multivalued nonexpansive mapping, respectively. Assume that
a single-valued and a multivalued nonexpansive mapping, respectively. Assume that  and
and  are commuting mappings. Then there exists a point
are commuting mappings. Then there exists a point  such that
such that  .
.
Corollary 3.5.
Let  be a nonempty bounded closed convex subset of a uniformly convex Banach space
be a nonempty bounded closed convex subset of a uniformly convex Banach space  , and let
, and let  be a multivalued mapping satisfying the Suzuki condition (C). Then
be a multivalued mapping satisfying the Suzuki condition (C). Then  has a fixed point.
has a fixed point.
Corollary 3.6.
Let  be a nonempty closed convex bounded subset of a uniformly convex Banach space
be a nonempty closed convex bounded subset of a uniformly convex Banach space  , and let
, and let  be a nonexpansive multivalued mapping. Then
be a nonexpansive multivalued mapping. Then  has a fixed point.
has a fixed point.
4. Strictly 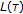 Spaces
Spaces
Definition 4.1.
Let  be a Banach space and let
be a Banach space and let  be a linear topology on
be a linear topology on  . We say that
. We say that  is a strictly
is a strictly  space if there exists a function
space if there exists a function  satisfying the following
satisfying the following
(i) is continuous;
is continuous;
(ii) is strictly increasing;
is strictly increasing;
(iii) , for every
, for every 
(iv) is strictly increasing;
is strictly increasing;
(v) , for every
, for every  and for every bounded and
and for every bounded and  -null sequence
-null sequence  , where
, where  is defined by
is defined by

In this case we also say that  satisfies the strict property
satisfies the strict property  with respect to
with respect to 
Example 4.2 (see [9]).
Let  be a positive
be a positive  -finite measure space. For every
-finite measure space. For every  , consider the Banach space
, consider the Banach space  with the usual norm. Let
with the usual norm. Let  be the topology of convergence locally in measure (clm). Then
be the topology of convergence locally in measure (clm). Then  endowed with the clm-topology satisfies the property
endowed with the clm-topology satisfies the property  with
with 
Definition 4.3.
Let  be a Banach space and let
be a Banach space and let  be a linear topology on
be a linear topology on  which is weaker than the norm topology. Let
which is weaker than the norm topology. Let  be a closed convex bounded subset of
be a closed convex bounded subset of  ; then for
; then for  we write
we write  We say that
We say that  has property (
has property ( ) if for every
) if for every  the set
the set  is a nonempty and norm-compact subset of
is a nonempty and norm-compact subset of  .
.
Theorem 4.4.
Let  be a strictly
be a strictly  Banach space and let
Banach space and let  be a nonempty closed convex bounded subset of
be a nonempty closed convex bounded subset of  satisfying the property
satisfying the property  . Suppose, in addition, that
. Suppose, in addition, that  is
is  -sequentially compact. If
-sequentially compact. If  satisfies the condition
satisfies the condition  , and if
, and if  is an upper semicontinuous mapping, then
is an upper semicontinuous mapping, then  has a fixed point.
has a fixed point.
Proof.
First, we find an approximate fixed point sequence. Choose  and
and  . Define
. Define

Let  be chosen in such a way that
be chosen in such a way that

Similarly, put  ; again we choose
; again we choose  in such a way that
in such a way that

In this way, we will find a sequence  in
in  such that
such that  , where
, where  and
and

Therefore, for every natural number  we have
we have

from which it follows that

Our assumption now gives

Hence

We now apply Lemma 2.8 to conclude that  where
where  . Since
. Since  is
is  -sequentially compact, by passing to a subsequence, we may assume that
-sequentially compact, by passing to a subsequence, we may assume that  is
is  -convergent to
-convergent to  Now we are going to show that
Now we are going to show that

Taking any  , by the compactness of
, by the compactness of  , we can find
, we can find  such that
such that  . On the other hand, there is a natural number
. On the other hand, there is a natural number  such that for every
such that for every  we have
we have  . This implies that
. This implies that

and hence from the assumption we obtain

Therefore,

Since  is compact, the sequence
is compact, the sequence  has a convergent subsequence
has a convergent subsequence  with
with  . It follows that
. It follows that

On the other hand, we have that  Since
Since  is strictly increasing, it follows that
is strictly increasing, it follows that  Hence
Hence  and so
and so  . Now we define the mapping
. Now we define the mapping

by  . From [10, Proposition
. From [10, Proposition  ], we know that the mapping
], we know that the mapping  is upper semicontinuous. Since
is upper semicontinuous. Since  is a compact convex set, we can apply the Kakutani-Bohnenblust-Karlin Theorem (see [11]) to obtain a fixed point for
is a compact convex set, we can apply the Kakutani-Bohnenblust-Karlin Theorem (see [11]) to obtain a fixed point for  and hence for
and hence for  .
.
Corollary 4.5.
Let  be a strictly
be a strictly  Banach space and let
Banach space and let  be a nonempty closed convex bounded subset of
be a nonempty closed convex bounded subset of  satisfying the property
satisfying the property  . Suppose, in addition, that
. Suppose, in addition, that  is
is  -sequentially compact. If
-sequentially compact. If  is a nonexpansive mapping, then
is a nonexpansive mapping, then  has a fixed point.
has a fixed point.
Corollary 4.6.
Let  be a strictly
be a strictly  Banach space and let
Banach space and let  be a nonempty closed convex and bounded subset of
be a nonempty closed convex and bounded subset of  satisfying the property
satisfying the property  . Suppose, in addition, that
. Suppose, in addition, that  is
is  -sequentially compact. If
-sequentially compact. If  is a continuous mapping satisfying the condition (C), then
is a continuous mapping satisfying the condition (C), then  has a fixed point.
has a fixed point.
Finally we mention that by Example 2.2, this corollary generalizes the recent result of Domínguez-Benavides et al. [4].
References
Suzuki T: Fixed point theorems and convergence theorems for some generalized nonexpansive mappings. Journal of Mathematical Analysis and Applications 2008,340(2):1088–1095. 10.1016/j.jmaa.2007.09.023
Abkar A, Eslamian M: A fixed point theorem for generalized nonexpansive multivalued mapping. to appear in Fixed Point Theory
Dhompongsa S, Kaewcharoen A, Kaewkhao A: The Domínguez-Lorenzo condition and multivalued nonexpansive mappings. Nonlinear Analysis. Theory, Methods & Applications 2006,64(5):958–970. 10.1016/j.na.2005.05.051
Domínguez-Benavides T, García-Falset J, Llorens-Fuster E, Lorenzo-Ramírez P: Fixed point properties and proximinality in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,71(5–6):1562–1571. 10.1016/j.na.2008.12.048
Dhompongsa S, Inthakon W, Kaewkhao A: Edelstein's method and fixed point theorems for some generalized nonexpansive mappings. Journal of Mathematical Analysis and Applications 2009,350(1):12–17. 10.1016/j.jmaa.2008.08.045
Goebel K, Kirk WA: Iteration processes for nonexpansive mappings. In Topological Methods in Nonlinear Functional Analysis. Volume 21. American Mathematical Society, Providence, RI, USA; 1983:115–123.
Goebel K: On a fixed point theorem for multivalued nonexpansive mappings. 1975, 29: 70–72.
Lim TC: A fixed point theorem for multivalued nonexpansive mappings in a uniformly convex Banach space. Bulletin of the American Mathematical Society 1974, 80: 1123–1126. 10.1090/S0002-9904-1974-13640-2
Domínguez-Benavides T, García-Falset J, Japón-Pineda MA: The -fixed point property for nonexpansive mappings. Abstract and Applied Analysis 1998,3(3–4):343–362. 10.1155/S1085337598000591
Hu S, Papageorgiou NS: Handbook of Multivalued Analysis, Mathematics and Its Applications. Volume 1. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:xvi+964.
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abkar, A., Eslamian, M. Fixed Point Theorems for Suzuki Generalized Nonexpansive Multivalued Mappings in Banach Spaces. Fixed Point Theory Appl 2010, 457935 (2010). https://doi.org/10.1155/2010/457935
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/457935
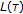 Spaces
Spaces