- Research Article
- Open access
- Published:
Existence Theorems for Generalized Distance on Complete Metric Spaces
Fixed Point Theory and Applications volume 2010, Article number: 397150 (2010)
Abstract
We first introduce the new concept of a distance called  -distance, which generalizes
-distance, which generalizes  -distance, Tataru's distance, and
-distance, Tataru's distance, and  -distance. Then we prove a new minimization theorem and a new fixed point theorem by using a
-distance. Then we prove a new minimization theorem and a new fixed point theorem by using a  -distance on a complete metric space. Our results extend and unify many known results due to Caristi, Ćirić, Ekeland, Kada-Suzuki-Takahashi, Kannan, Ume, and others.
-distance on a complete metric space. Our results extend and unify many known results due to Caristi, Ćirić, Ekeland, Kada-Suzuki-Takahashi, Kannan, Ume, and others.
1. Introduction
The Banach contraction principle [1], Ekeland's  -variational principle [2], and Caristi's fixed point theorem [3] are very useful tools in nonlinear analysis, control theory, economic theory, and global analysis. These theorems are extended by several authors in different directions.
-variational principle [2], and Caristi's fixed point theorem [3] are very useful tools in nonlinear analysis, control theory, economic theory, and global analysis. These theorems are extended by several authors in different directions.
Takahashi [4] proved the following minimization theorem. Let  be a complete metric space and let
be a complete metric space and let  be a proper lower semicontinuous function, bounded from below. Suppose that, for each
be a proper lower semicontinuous function, bounded from below. Suppose that, for each  with
with  there exists
there exists  such that
such that  and
and  Then there exists
Then there exists  such that
such that  Some authors [5–7] have generalized and extended this minimization theorem in complete metric spaces.
Some authors [5–7] have generalized and extended this minimization theorem in complete metric spaces.
In 1996, Kada et al. [5] introduced the concept of  -distance on a metric space as follows. Let
-distance on a metric space as follows. Let  be a metric space with metric
be a metric space with metric  . Then a function
. Then a function  is called a
is called a  -distance on
-distance on  if the followings are satisfied.
if the followings are satisfied.
(1) for any
for any  .
.
(2)For any  is lower semicontinuous.
is lower semicontinuous.
(3)For any  , there exists
, there exists  such that
such that  and
and  imply
imply 
They gave some examples of  -distance and improved Caristi's fixed point theorem [3], Ekeland's variational principle [2], and Takahashi's nonconvex minimization theorem [4]. The fixed point theorems with respect to a
-distance and improved Caristi's fixed point theorem [3], Ekeland's variational principle [2], and Takahashi's nonconvex minimization theorem [4]. The fixed point theorems with respect to a  -distance were proved in [8–12].
-distance were proved in [8–12].
Throughout this paper we denote by  the set of all positive integers, by
the set of all positive integers, by  the set of all real numbers, and by
the set of all real numbers, and by  the set of all nonnegative real numbers.
the set of all nonnegative real numbers.
Recently, Suzuki [6] introduced the concept of  -distance on a metric space, which generalizes Tataru's distance [13] as follows. Let
-distance on a metric space, which generalizes Tataru's distance [13] as follows. Let  be a metric space with metric
be a metric space with metric  .
.
Then a function  from
from  into
into  is called
is called  -distance on
-distance on  if there exists a function
if there exists a function  from
from  into
into  and the followings are satisfied:
and the followings are satisfied:
(τ1) for all
for all  ;
;
(τ2) and
and  for all
for all  and
and  , and
, and  is concave and continuous in its second variable;
is concave and continuous in its second variable;
(τ3) and
and  imply
imply  for all
for all  ;
;
(τ4) and
and  imply
imply  ;
;
(τ5) and
and  imply
imply  .
.
In this paper, we first introduce the new concept of a distance called  -distance, which generalizes
-distance, which generalizes  -distance, Tataru's distance, and
-distance, Tataru's distance, and  -distance. Then we prove a new minimization theorem and a new fixed point theorem by using
-distance. Then we prove a new minimization theorem and a new fixed point theorem by using  -distance on a complete metric space. Our results extend and unify many known results due to Caristi [3], Ćirić [14], Ekeland [2], Takahashi [4], Kada et al. [5], Kannan [15], Suzuki [6], and Ume [7, 12] and others.
-distance on a complete metric space. Our results extend and unify many known results due to Caristi [3], Ćirić [14], Ekeland [2], Takahashi [4], Kada et al. [5], Kannan [15], Suzuki [6], and Ume [7, 12] and others.
2. Preliminaries
Definition 2.1.
Let  be metric space with metric
be metric space with metric  . Then a function
. Then a function  from
from  into
into  is called
is called  -distance on
-distance on  if there exists a function
if there exists a function  from
from  into
into  such that
such that
(u1) for all
for all  ;
;
(u2) and
and  for all
for all  and
and  , and for any
, and for any  and for every
and for every  , there exists
, there exists  such that
such that  ,
,  ,
,  and
and  imply
imply

(u3)

imply

for all  ;
;
(u4)

imply

or

imply

(u)

imply

or

imply

Remark 2.2.
Suppose that  is a mapping satisfying (u2)
is a mapping satisfying (u2) (u5). Then there exists a mapping
(u5). Then there exists a mapping  from
from  into
into  such that
such that  is nondecreasing in its third and fourth variable, respectively, satisfying (u2)
is nondecreasing in its third and fourth variable, respectively, satisfying (u2) (u5)
(u5) , where (u2)
, where (u2) (u5)
(u5) stand for substituting
stand for substituting  for
for  in (u2)
in (u2) (u5), respectively.
(u5), respectively.
Proof.
Suppose that  is a mapping satisfying (u2)
is a mapping satisfying (u2) (u5). Define a function
(u5). Define a function  by
by

By (2.12), we have  and
and  for all
for all  and
and  . Also it follows from (2.12) that
. Also it follows from (2.12) that  is nondecreasing in its third and fourth variable, respectively.
is nondecreasing in its third and fourth variable, respectively.
We shall prove the following:

Suppose that (2.13) does not hold. Then

By virtue of (2.12) and (2.14), we have

Combining (u2) and (2.14), we have the following:

Due to (2.16), we get that

From (2.16) and (2.17), we obtain the following.



In terms of (2.19) and (2.20), we deduce that

In view of (2.21), we get that

On account of (2.20), we know the following:

Using (2.16), (2.18), (2.19), and (2.23), we have the following:

By (2.24), we have

By virtue of (2.15), (2.19), (2.20), (2.22), and (2.25), we have  which is a contradiction. Hence (u2)
which is a contradiction. Hence (u2) holds. From (2.12) and (u2)~(u5), it follows that (u3)
holds. From (2.12) and (u2)~(u5), it follows that (u3) ~(u5)
~(u5) are satisfied.
are satisfied.
Remark 2.3.
From Remark 2.2, we may assume that  is nondecreasing in its third and fourth variables, respectively, for a function
is nondecreasing in its third and fourth variables, respectively, for a function  satisfying (u2)
satisfying (u2) (u5).
(u5).
We give some examples of  -distance.
-distance.
Example 2.4.
Let  be the set of real numbers with the usual metric and let
be the set of real numbers with the usual metric and let  be defined by
be defined by  . Then
. Then  is a
is a  -distance on
-distance on  but not a
but not a  -distance on
-distance on  .
.
Proof.
Define  by
by  for all
for all  and
and  . Then
. Then  and
and  satisfy (u1)~(u5). But for an arbitrary function
satisfy (u1)~(u5). But for an arbitrary function  and for all sequences
and for all sequences  ,
,  and
and  of
of  such that
such that

since the limit of the sequence  and the limit of the sequence
and the limit of the sequence  do not depend on
do not depend on  and
and  , the limit of the sequence
, the limit of the sequence  may not be
may not be  . This does not satisfy (
. This does not satisfy ( 5). Hence
5). Hence  is not a
is not a  -distance on
-distance on  . Therefore
. Therefore  is a
is a  -distance on
-distance on  but not a
but not a  -distance on
-distance on  .
.
Example 2.5.
Let  be a
be a  -distance on a metric space
-distance on a metric space  . Then
. Then  is also a
is also a  -distance on
-distance on  .
.
Proof.
Since  is a
is a  -distance, there exists a function
-distance, there exists a function  satisfying (
satisfying ( 1)~(
1)~( 5). Define
5). Define  by
by

Then it is easy to see that  and
and  satisfy (u2)~(u5). Thus
satisfy (u2)~(u5). Thus  is a
is a  -distance on
-distance on  .
.
Example 2.6.
Let  be a normed space with norm
be a normed space with norm  . Then a function
. Then a function  defined by
defined by  for every
for every  is a
is a  -distance on
-distance on  but not a
but not a  -distance.
-distance.
Proof.
Let  be as in the proof of Example 2.4. Then it is clear that
be as in the proof of Example 2.4. Then it is clear that  satisfies
satisfies  and
and  satisfies (u2)~(u5) on
satisfies (u2)~(u5) on  but
but  does not satisfy
does not satisfy  . Thus
. Thus  is a
is a  -distance on
-distance on  but not a
but not a  -distance.
-distance.
Example 2.7.
Let  be a normed space with norm
be a normed space with norm  . Then a function
. Then a function  defined by
defined by  for every
for every  is a
is a  -distance on
-distance on  .
.
Proof.
Define  by
by  for all
for all  and
and  . Then
. Then  satisfies
satisfies  and
and  satisfies (u2)~(u5). Thus
satisfies (u2)~(u5). Thus  is a
is a  -distance on
-distance on  .
.
Example 2.8.
Let  be a
be a  -distance on a metric space
-distance on a metric space  and let
and let  be a positive real number. Then a function
be a positive real number. Then a function  from
from  into
into  defined by
defined by  for every
for every  is also a
is also a  -distance on
-distance on  .
.
Proof.
Since  is a
is a  -distance on
-distance on  , there exists a function
, there exists a function  satisfying (u2)
satisfying (u2) ~(u5)
~(u5) and
and  satisfies (u1). Define
satisfies (u1). Define  by
by  for all
for all  and
and  . Then it is clear that
. Then it is clear that  satisfies
satisfies  and
and  satisfies (u2)~(u5). Thus
satisfies (u2)~(u5). Thus  is a
is a  -distance on
-distance on  .
.
The following examples can be easily obtained from Remark 2.3.
Example 2.9.
Let  be a metric space with metric
be a metric space with metric  and let
and let  be a
be a  -distance on
-distance on  such that
such that  is a lower semicontinuous in its first variable. Then a function
is a lower semicontinuous in its first variable. Then a function  defined by
defined by  for all
for all  is a
is a  -distance on
-distance on  .
.
Example 2.10.
Let  be a metric space with metric
be a metric space with metric  . Let
. Let  be a
be a  -distance on
-distance on  and let
and let  be a function from
be a function from  into
into  . Then a function
. Then a function  defined by
defined by

is a  -distance on
-distance on  .
.
Remark 2.11.
It follows from Example 2.4 to Example 2.10 that  -distance is a proper extension of
-distance is a proper extension of  -distance.
-distance.
Definition 2.12.
Let  be a metric space with a metric
be a metric space with a metric  and let
and let  be a
be a  -distance on
-distance on  . Then a sequence
. Then a sequence  of
of  is called
is called  -Cauchy if there exists a function
-Cauchy if there exists a function  satisfying (u2)~(u5) and a sequence
satisfying (u2)~(u5) and a sequence  of
of  such that
such that

or

The following lemmas play an important role in proving our theorems.
Lemma 2.13.
Let  be a metric space with a metric
be a metric space with a metric  and let
and let  be a
be a  -distance on
-distance on  . If
. If  is a
is a  -Cauchy sequence, then
-Cauchy sequence, then  is a Cauchy sequence.
is a Cauchy sequence.
Proof.
By assumption, there exists a function  from
from  into
into  satisfying (u2)~(u5) and a sequence
satisfying (u2)~(u5) and a sequence  of
of  such that
such that

or

Then from (u5), we have  . This means that
. This means that  is a Cauchy sequence.
is a Cauchy sequence.
Lemma 2.14.
Let  be a metric space with a metric
be a metric space with a metric  and let
and let  be a
be a  -distance on
-distance on  .
.
(1)If sequences  and
and  of
of  satisfy
satisfy  and
and 
 for some
for some  , then
, then  .
.
(2)If  and
and  , then
, then  .
.
(3)Suppose that sequences  and
and  of
of  satisfy
satisfy  and
and  for some
for some  , then
, then  .
.
(4)If  and
and  , then
, then  .
.
Proof.
-
(1)
Let
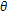 be a function from
be a function from 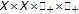 into
into 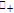 satisfying (u2)~(u5). From Remark 2.3 and hypotheses,
satisfying (u2)~(u5). From Remark 2.3 and hypotheses, 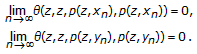 (2.33)
(2.33)
By (u5),  .
.
-
(2)
In (1), putting
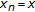 and
and  for all
for all  , (2) holds.
, (2) holds.
By method similar to (1) and (2), results of (3) and (4) follow.
Lemma 2.15.
Let  be a metric space with a metric
be a metric space with a metric  and let
and let  be a
be a  -distance on
-distance on  . Suppose that a sequence
. Suppose that a sequence  of
of  satisfies
satisfies

or

Then  is a
is a  -Cauchy sequence and
-Cauchy sequence and  is a Cauchy sequence.
is a Cauchy sequence.
Proof.
Since  is a
is a  -distance on
-distance on  , there exists a function
, there exists a function  satisfying (u2)
satisfying (u2) (u5). Suppose
(u5). Suppose  . Let
. Let  . Then we have
. Then we have  . Let
. Let  be an arbitrary subsequence of
be an arbitrary subsequence of  . By assumption and (u2), there exists a subsequence
. By assumption and (u2), there exists a subsequence  of
of  such that
such that

From (u4), we obtain

Since  is an arbitrary sequence of
is an arbitrary sequence of  ,
,  is also an arbitrary sequence of
is also an arbitrary sequence of  . Hence
. Hence

Therefore we get

This implies that  is a
is a  -Cauchy sequence. By Lemma 2.13,
-Cauchy sequence. By Lemma 2.13,  is a Cauchy sequence. Similarly, if
is a Cauchy sequence. Similarly, if  we can prove that
we can prove that  is also a Cauchy sequence.
is also a Cauchy sequence.
3. Minimization Theorems and Fixed Point Theorems
The following theorem is a generalization of Takahashi's minimization theorem [4].
Theorem 3.1.
Let  be a metric space with metric
be a metric space with metric  , let
, let  be a proper function which is bounded from below, and let
be a proper function which is bounded from below, and let  be a function such that, one has the following.
be a function such that, one has the following.
(i) for all
for all  .
.
(ii)For any sequence  in
in  satisfying
satisfying

there exists  such that
such that 

(iii) imply
imply  .
.
(iv)For every  with
with  , there exists
, there exists  such that
such that

where a function  is defined by
is defined by

for all  . Then, there exists
. Then, there exists  such that
such that

Proof.
Suppose  for all
for all  . For each
. For each  , let
, let

Then, by condition (iv) and (3.6),  is nonempty for each
is nonempty for each  . From condition (i) and (3.6), we obtain
. From condition (i) and (3.6), we obtain

For each  , let
, let

Choose  with
with  . Then, from (3.7) and (3.8), there exists a sequence
. Then, from (3.7) and (3.8), there exists a sequence  in
in  such that
such that

for all  .
.
From (3.6), (3.8) and (3.9), we have


By (3.10),  is a nonincreasing sequence of real numbers and so it converges. Therefore, from (3.11) there is some
is a nonincreasing sequence of real numbers and so it converges. Therefore, from (3.11) there is some  such that
such that

From condition (i) and (3.10), we get

for all  . From (3.12) and (3.13), we have
. From (3.12) and (3.13), we have

Thus, by condition (ii), (3.12), and (3.13), there exists  such that
such that



From (3.13), (3.16), and (3.17), we have

From (3.6), (3.8), and (3.18), it follows that

Taking the limit in inequality (3.19) when  tends to infinity, we have
tends to infinity, we have

From (3.12), (3.16), and (3.20), we have

On the other hand, by condition (iv) and (3.6), we have the following property:

From (3.7), (3.8), (3.19), and (3.22), we have

From (3.6), (3.12), (3.21), (3.22), (3.23), it follows that

From (3.21), (3.22), and (3.24), we have

By method similar to (3.22) (3.25),
(3.25),

From (3.25), (3.26), and condition (i), we obtain

From (3.25), (3.27), and condition (iii), we obtain

This is a contradiction from (3.26).
Corollary 3.2.
Let  be a complete metric space with metric
be a complete metric space with metric  , and let
, and let  be a proper lower semicontinuous function which is bounded from below. Assume that there exists a
be a proper lower semicontinuous function which is bounded from below. Assume that there exists a  -distance
-distance  on
on  such that for each
such that for each  with
with  , there exists
, there exists  with
with  and
and  . Then there exists
. Then there exists  such that
such that  .
.
Proof.
Let  be a mapping such that
be a mapping such that

for all  . It follows easily from Definition 2.12, Lemmas 2.13, 2.14, and 2.15, and (u3) that conditions of Corollary 3.2 satisfy all conditions of Theorem 3.1. Thus, we obtain result of Corollary 3.2.
. It follows easily from Definition 2.12, Lemmas 2.13, 2.14, and 2.15, and (u3) that conditions of Corollary 3.2 satisfy all conditions of Theorem 3.1. Thus, we obtain result of Corollary 3.2.
Remark 3.3.
Corollary 3.2 is a generalization of Kadaet al. [5, Theorem  ] and Suzuki [6, Theorem
] and Suzuki [6, Theorem  ].
].
From Lemmas 2.13, 2.14, and 2.15, we have the following fixed point theorem.
Theorem 3.4.
Let  be a complete metric space with metric
be a complete metric space with metric  , let
, let  be a
be a  -distance on
-distance on  and let
and let  be a selfmapping of
be a selfmapping of  . Suppose that there exists
. Suppose that there exists  such that
such that

for all  and
and

for every  with
with  . Then there exists
. Then there exists  such that
such that  and
and  . Moreover, if
. Moreover, if  , then
, then  ,
,  .
.
Proof.
By method similar to [12, Lemma  ], for every
], for every  ,
,

Define  by
by

for every  . By Example 2.10,
. By Example 2.10,  is a
is a  -distance on
-distance on  . Then we get
. Then we get

for all  . Thus we have
. Thus we have

for all  . Now we have
. Now we have

Thus

By Lemma 2.15,  is a
is a  -Cauchy and hence
-Cauchy and hence  is a Cauchy from Lemma 2.13. Since
is a Cauchy from Lemma 2.13. Since  is complete and
is complete and  is a
is a  -Cauchy, there exists
-Cauchy, there exists  such that
such that

Suppose  . Then, by hypothesis, we have
. Then, by hypothesis, we have

This is a contradiction. Therefore we have  . If
. If  , we have
, we have  and hence
and hence  . To prove unique fixed point of
. To prove unique fixed point of  , let
, let  and
and  . Then, by hypothesis, we have
. Then, by hypothesis, we have

Thus

By Lemma 2.14, we have  .
.
From Theorem 3.4, we have the following corollary which generalizes the results of Ćirić [14], Kannan [15], and Ume [12].
Corollary 3.5.
Let  be a complete metric space with metric
be a complete metric space with metric  , let
, let  be a
be a  -distance on
-distance on  and let
and let  be a selfmapping of
be a selfmapping of  . Suppose that there exists
. Suppose that there exists  such that
such that

for all  and
and

for every  with
with  . Then there exists
. Then there exists  such that
such that  and
and  . Moreover, if
. Moreover, if  , then
, then  and
and  .
.
Proof.
Since a  -distance is a
-distance is a  -distance, Corollary 3.5 follows from Theorem 3.4.
-distance, Corollary 3.5 follows from Theorem 3.4.
The following corollary is a generalization of Suzuki's fixed point theorem [6].
Corollary 3.6.
Let  and
and  be as in Corollary 3.5. Suppose that there exists
be as in Corollary 3.5. Suppose that there exists  such that
such that

for all  . Assume that if
. Assume that if

then  . Then there exists
. Then there exists  such that
such that  and
and  . Moreover, if
. Moreover, if  , then
, then  and
and  .
.
Proof.
Let  and
and  be as in Theorem 3.4. Then from Theorem 3.4 and hypotheses of Corollary 3.6, we have the following properties.
be as in Theorem 3.4. Then from Theorem 3.4 and hypotheses of Corollary 3.6, we have the following properties.
(1) is a Cauchy sequence.
is a Cauchy sequence.
(2)There exists  such that
such that  .
.
(3)One has

(4)There exists

(5)One has

By (1)~(5) and hypotheses, we have  . The remainders are same as Theorem 3.4.
. The remainders are same as Theorem 3.4.
The following theorem is a generalization of Caristi's fixed point theorem [3].
Theorem 3.7.
Let  be a metric space with metric
be a metric space with metric  , let
, let  be a proper function which is bounded from below, and let
be a proper function which is bounded from below, and let  be a function satisfying (i), (ii), and (iii) of Theorem 3.1. Let
be a function satisfying (i), (ii), and (iii) of Theorem 3.1. Let  be a selfmapping of
be a selfmapping of  such that
such that

where a function  is defined by
is defined by

for all  . Then, there exists
. Then, there exists  such that
such that

Proof.
Suppose  for all
for all  . Then, by Theorem 3.1, there exists
. Then, by Theorem 3.1, there exists  such that
such that

Since

we have

By hypothesis, we obtain

Hence

By conditions (i) and (iii) of Theorem 3.1, it follows that

This is a contradiction.
Corollary 3.8.
Let  be a complete metric space with metric
be a complete metric space with metric  and let
and let  be a proper lower semicontinuous function which is bounded from below. Let
be a proper lower semicontinuous function which is bounded from below. Let  be a
be a  -distance on
-distance on  . Suppose that
. Suppose that  is a selfmapping of
is a selfmapping of  such that
such that

for all  . Then there exists
. Then there exists  such that
such that

Proof.
Define  by
by

for all  . Then, by Definition 2.12 and Lemmas 2.13, 2.14, and 2.15, we can easily show that conditions of Corollary 3.8 satisfy all conditions of Theorem 3.7. Thus, Corollary 3.8 follows from Theorem 3.7.
. Then, by Definition 2.12 and Lemmas 2.13, 2.14, and 2.15, we can easily show that conditions of Corollary 3.8 satisfy all conditions of Theorem 3.7. Thus, Corollary 3.8 follows from Theorem 3.7.
Remark 3.9.
Since a  -distance and a
-distance and a  -distance are a
-distance are a  -distance, Corollary 3.8 is a generalization of Kada-Suzuki-Takahashi [5, Theorem
-distance, Corollary 3.8 is a generalization of Kada-Suzuki-Takahashi [5, Theorem  ] and Suzuki [6, Theorem
] and Suzuki [6, Theorem  ].
].
The following theorem is a generalization of Ekeland's  -variational principle [2].
-variational principle [2].
Theorem 3.10.
Let  be a complete metric space with metric
be a complete metric space with metric  , let
, let  be a proper lower semicontinuous function which is bounded from below, and let
be a proper lower semicontinuous function which is bounded from below, and let  be a function satisfying (i), (ii), and (iii) of Theorem 3.1. Then the following (1) and (2) hold.
be a function satisfying (i), (ii), and (iii) of Theorem 3.1. Then the following (1) and (2) hold.
(1)For each  with
with  , there exists
, there exists  such that
such that  and
and

for all  with
with  where a function
where a function  is defined by
is defined by

for all  .
.
(2)For each  and
and  with
with  , and
, and

there exists  such that
such that  ,
,

for all  with
with 
Proof.
( ) Let
) Let  be such that
be such that  , and let
, and let

Then, by hypotheses,  is nonempty and closed. Thus
is nonempty and closed. Thus  is a complete metric space. Hence we may prove that there exists an element
is a complete metric space. Hence we may prove that there exists an element  such that
such that  for all
for all  with
with  Suppose not. Then, for every
Suppose not. Then, for every  , there exists
, there exists  such that
such that  and
and  By Theorem 3.1, there exists
By Theorem 3.1, there exists  such that
such that

Again for  , there exists
, there exists  such that
such that  and
and

Hence we have  and
and  Similarly, there exists
Similarly, there exists  such that
such that  and
and

Thus we have  and
and  From conditions (i) and (iii) of Theorem 3.1, we obtain
From conditions (i) and (iii) of Theorem 3.1, we obtain

This is a contradiction. The proof of (1) is complete.
-
(2)
Let
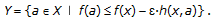 (3.70)
(3.70)
Then  is nonempty and closed. Hence
is nonempty and closed. Hence  is complete. As in the proof of (1), we have that there exists
is complete. As in the proof of (1), we have that there exists  such that
such that

for every  with
with  On the other hand, since
On the other hand, since  , we have
, we have

This completes the proof of (2).
Corollary 3.11.
Let  and
and  be as in Corollary 3.8. Then the following (1) and (2) hold.
be as in Corollary 3.8. Then the following (1) and (2) hold.
(1)For each  with
with  , there exists
, there exists  such that
such that  and
and

for all  with
with 
(2)For each  and
and  with
with  , and
, and

there exists  such that
such that  ,
,

for all  with
with 
Proof.
By method similar to Corollary 3.8, Corollary 3.11 follows from Theorem 3.10.
Remark 3.12.
Corollary 3.11 is a generalization of Suzuki [6, Theorem  ].
].
References
Banach S: Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundamenta Mathematicae 1992, 3: 133–181.
Ekeland I: Nonconvex minimization problems. Bulletin of the American Mathematical Society 1979,1(3):443–474. 10.1090/S0273-0979-1979-14595-6
Caristi J: Fixed point theorems for mappings satisfying inwardness conditions. Transactions of the American Mathematical Society 1976, 215: 241–251.
Takahashi W: Minimization theorems and fixed point theorems. In Nonlinear Analysis and Mathematical Economics. Volume 829. Edited by: Maruyama T. RIMS Kokyuroku; 1993:175–191.
Kada O, Suzuki T, Takahashi W: Nonconvex minimization theorems and fixed point theorems in complete metric spaces. Mathematica Japonica 1996,44(2):381–391.
Suzuki T: Generalized distance and existence theorems in complete metric spaces. Journal of Mathematical Analysis and Applications 2001,253(2):440–458. 10.1006/jmaa.2000.7151
Ume J-S: Some existence theorems generalizing fixed point theorems on complete metric spaces. Mathematica Japonica 1994,40(1):109–114.
Shioji N, Suzuki T, Takahashi W: Contractive mappings, Kannan mappings and metric completeness. Proceedings of the American Mathematical Society 1998,126(10):3117–3124. 10.1090/S0002-9939-98-04605-X
Suzuki T: Fixed point theorems in complete metric spaces. In Nonlinear Analysis and Convex Analysis. Volume 939. Edited by: Takahashi W. RIMS Kokyuroku; 1996:173–182.
Suzuki T: Several fixed point theorems in complete metric spaces. Yokohama Mathematical Journal 1997,44(1):61–72.
Suzuki T, Takahashi W: Fixed point theorems and characterizations of metric completeness. Topological Methods in Nonlinear Analysis 1996,8(2):371–382.
Ume J-S: Fixed point theorems related to Ćirić's contraction principle. Journal of Mathematical Analysis and Applications 1998,225(2):630–640. 10.1006/jmaa.1998.6030
Tataru D: Viscosity solutions of Hamilton-Jacobi equations with unbounded nonlinear terms. Journal of Mathematical Analysis and Applications 1992,163(2):345–392. 10.1016/0022-247X(92)90256-D
Ćirić LjB: A generalization of Banach's contraction principle. Proceedings of the American Mathematical Society 1974, 45: 267–273.
Kannan R: Some results on fixed points. II. The American Mathematical Monthly 1969, 76: 405–408. 10.2307/2316437
Acknowledgments
The author would like to thank the referees for useful comments and suggestions. This work was supported by the Korea Research Foundation (KRF) Grant funded by the Korea government (MEST) (2009-0073655).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ume, J. Existence Theorems for Generalized Distance on Complete Metric Spaces. Fixed Point Theory Appl 2010, 397150 (2010). https://doi.org/10.1155/2010/397150
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/397150
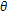 be a function from
be a function from 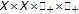 into
into 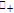 satisfying (u2)~(u5). From Remark 2.3 and hypotheses,
satisfying (u2)~(u5). From Remark 2.3 and hypotheses, 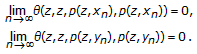
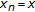 and
and  for all
for all  , (2) holds.
, (2) holds.