- Research Article
- Open access
- Published:
Strong Convergence Theorems of a New General Iterative Process with Meir-Keeler Contractions for a Countable Family of 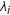 -Strict Pseudocontractions in
-Strict Pseudocontractions in 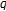 -Uniformly Smooth Banach Spaces
-Uniformly Smooth Banach Spaces
Fixed Point Theory and Applications volume 2010, Article number: 354202 (2010)
Abstract
We introduce a new iterative scheme with Meir-Keeler contractions for strict pseudocontractions in  -uniformly smooth Banach spaces. We also discuss the strong convergence theorems for the new iterative scheme in
-uniformly smooth Banach spaces. We also discuss the strong convergence theorems for the new iterative scheme in  -uniformly smooth Banach space. Our results improve and extend the corresponding results announced by many others.
-uniformly smooth Banach space. Our results improve and extend the corresponding results announced by many others.
1. Introduction
Throughout this paper, we denote by  and
and  a real Banach space and the dual space of
a real Banach space and the dual space of  , respectively. Let
, respectively. Let  be a subset of
be a subset of  , and lrt
, and lrt  be a non-self-mapping of
be a non-self-mapping of  . We use
. We use  to denote the set of fixed points of
to denote the set of fixed points of  .
.
The norm of a Banach space  is said to be Gâteaux differentiable if the limit
is said to be Gâteaux differentiable if the limit

exists for all  ,
,  on the unit sphere
on the unit sphere  . If, for each
. If, for each  , the limit (1.1) is uniformly attained for
, the limit (1.1) is uniformly attained for  , then the norm of
, then the norm of  is said to be uniformly Gâteaux differentiable. The norm of
is said to be uniformly Gâteaux differentiable. The norm of  is said to be Fréchet differentiable if, for each
is said to be Fréchet differentiable if, for each  , the limit (1.1) is attained uniformly for
, the limit (1.1) is attained uniformly for  . The norm of
. The norm of  is said to be uniformly Fréchet differentiable (or uniformly smooth) if the limit (1.1) is attained uniformly for
is said to be uniformly Fréchet differentiable (or uniformly smooth) if the limit (1.1) is attained uniformly for  .
.
Let  be the modulus of smoothness of
be the modulus of smoothness of  defined by
defined by

A Banach space  is said to be uniformly smooth if
is said to be uniformly smooth if  as
as  . Let
. Let  . A Banach space
. A Banach space  is said to be
is said to be  -uniformly smooth, if there exists a fixed constant
-uniformly smooth, if there exists a fixed constant  such that
such that  . It is well known that
. It is well known that  is uniformly smooth if and only if the norm of
is uniformly smooth if and only if the norm of  is uniformly Fréchet differentiable. If
is uniformly Fréchet differentiable. If  is
is  -uniformly smooth, then
-uniformly smooth, then  and
and  is uniformly smooth, and hence the norm of
is uniformly smooth, and hence the norm of  is uniformly Fréchet differentiable, in particular, the norm of
is uniformly Fréchet differentiable, in particular, the norm of  is Fréchet differentiable. Typical examples of both uniformly convex and uniformly smooth Banach spaces are
is Fréchet differentiable. Typical examples of both uniformly convex and uniformly smooth Banach spaces are  , where
, where  . More precisely,
. More precisely,  is
is  -uniformly smooth for every
-uniformly smooth for every  .
.
By a gauge we mean a continuous strictly increasing function  defined
defined  such that
such that  and
and  . We associate with a gauge
. We associate with a gauge  a (generally multivalued) duality map
a (generally multivalued) duality map  defined by
defined by

In particular, the duality mapping with gauge function  denoted by
denoted by  , is referred to the (generalized) duality mapping. The duality mapping with gauge function
, is referred to the (generalized) duality mapping. The duality mapping with gauge function  denoted by
denoted by  , is referred to the normalized duality mapping. Browder [1] initiated the study
, is referred to the normalized duality mapping. Browder [1] initiated the study  . Set for
. Set for 

Then it is known that  is the subdifferential of the convex function
is the subdifferential of the convex function  at
at  . It is well known that if
. It is well known that if  is smooth, then
is smooth, then  is single valued, which is denoted by
is single valued, which is denoted by  .
.
The duality mapping  is said to be weakly sequentially continuous if the duality mapping
is said to be weakly sequentially continuous if the duality mapping  is single valued and for any
is single valued and for any  with
with  ,
,  . Every
. Every  space has a weakly sequentially continuous duality map with the gauge
space has a weakly sequentially continuous duality map with the gauge  . Gossez and Lami Dozo [2] proved that a space with a weakly continuous duality mapping satisfies Opial's condition. Conversely, if a space satisfies Opial's condition and has a uniformly Gâteaux differentiable norm, then it has a weakly continuous duality mapping. We already know that in
. Gossez and Lami Dozo [2] proved that a space with a weakly continuous duality mapping satisfies Opial's condition. Conversely, if a space satisfies Opial's condition and has a uniformly Gâteaux differentiable norm, then it has a weakly continuous duality mapping. We already know that in  -uniformly smooth Banach space, there exists a constant
-uniformly smooth Banach space, there exists a constant  such that
such that

for all  .
.
Recall that a mapping  is said to be nonexpansive, if
is said to be nonexpansive, if

 is said to be a
is said to be a  -strict pseudocontraction in the terminology of Browder and Petryshyn [3], if there exists a constant
-strict pseudocontraction in the terminology of Browder and Petryshyn [3], if there exists a constant  such that
such that

for every  ,
,  , and
, and  for some
for some  . It is clear that (1.7) is equivalent to the following:
. It is clear that (1.7) is equivalent to the following:

The following famous theorem is referred to as the Banach contraction principle.
Theorem 1.1 (Banach [4]).
Let  be a complete metric space and let
be a complete metric space and let  be a contraction on
be a contraction on  , that is, there exists
, that is, there exists  such that
such that  for all
for all  . Then
. Then  has a unique fixed point.
has a unique fixed point.
Theorem 1.2 (Meir and Keeler [5]).
Let  be a complete metric space and let
be a complete metric space and let  be a Meir-Keeler contraction (MKC, for short) on
be a Meir-Keeler contraction (MKC, for short) on  , that is, for every
, that is, for every  , there exists
, there exists  such that
such that  implies
implies  for all
for all  . Then
. Then  has a unique fixed point.
has a unique fixed point.
This theorem is one of generalizations of Theorem 1.1, because contractions are Meir-Keeler contractions.
In a smooth Banach space, we define an operator  is strongly positive if there exists a constant
is strongly positive if there exists a constant  with the property
with the property

where  is the identity mapping and
is the identity mapping and  is the normalized duality mapping.
is the normalized duality mapping.
Attempts to modify the normal Mann's iteration method for nonexpansive mappings and  -strictly pseudocontractions so that strong convergence is guaranteed have recently been made; see, for example, [6–11] and the references therein.
-strictly pseudocontractions so that strong convergence is guaranteed have recently been made; see, for example, [6–11] and the references therein.
Kim and Xu [6] introduced the following iteration process:

where  is a nonexpansive mapping of
is a nonexpansive mapping of  into itself
into itself  is a given point. They proved the sequence
is a given point. They proved the sequence  defined by (1.10) converges strongly to a fixed point of
defined by (1.10) converges strongly to a fixed point of  , provided the control sequences
, provided the control sequences  and
and  satisfy appropriate conditions.
satisfy appropriate conditions.
Hu and Cai [12] introduced the following iteration process:

where  is non-self-
is non-self- -strictly pseudocontraction,
-strictly pseudocontraction,  is a contraction and
is a contraction and  is a strong positive linear bounded operator in Banach space. They have proved, under certain appropriate assumptions on the sequences
is a strong positive linear bounded operator in Banach space. They have proved, under certain appropriate assumptions on the sequences  , and
, and  , that
, that  defined by (1.11) converges strongly to a common fixed point of a finite family of
defined by (1.11) converges strongly to a common fixed point of a finite family of  -strictly pseudocontractions, which solves some variational inequality.
-strictly pseudocontractions, which solves some variational inequality.
Question 1.
Can Theorem 3.1 of Zhou [8], Theorem 2.2 of Hu and Cai [12] and so on be extended from finite  -strictly pseudocontraction to infinite
-strictly pseudocontraction to infinite  -strictly pseudocontraction?
-strictly pseudocontraction?
Question 2.
We know that the Meir-Keeler contraction (MKC, for short) is more general than the contraction. What happens if the contraction is replaced by the Meir-Keeler contraction?
The purpose of this paper is to give the affirmative answers to these questions mentioned above. In this paper we study a general iterative scheme as follows:

where  is non-self
is non-self  -strictly pseudocontraction,
-strictly pseudocontraction,  is a MKC contraction and
is a MKC contraction and  is a strong positive linear bounded operator in Banach space. Under certain appropriate assumptions on the sequences
is a strong positive linear bounded operator in Banach space. Under certain appropriate assumptions on the sequences  ,
,  ,
,  , and
, and  , that
, that  defined by (1.12) converges strongly to a common fixed point of an infinite family of
defined by (1.12) converges strongly to a common fixed point of an infinite family of  -strictly pseudocontractions, which solves some variational inequality.
-strictly pseudocontractions, which solves some variational inequality.
2. Preliminaries
In order to prove our main results, we need the following lemmas.
Lemma 2.1 (see [13]).
Let  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and
and  be a sequence in
be a sequence in  which satisfies the following condition:
which satisfies the following condition:  . Suppose that
. Suppose that  for all
for all  and
and  . Then,
. Then,  .
.
Lemma 2.2 (see Xu [14]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that  , where
, where  is a sequence in (0, 1) and
is a sequence in (0, 1) and  is a sequence in
is a sequence in  such that
such that
(i) ,
,
(ii) or
or  .
.
Then  .
.
Lemma 2.3 (see [15] demiclosedness principle).
Let  be a nonempty closed convex subset of a reflexive Banach space
be a nonempty closed convex subset of a reflexive Banach space  which satisfies Opial's condition, and suppose
which satisfies Opial's condition, and suppose  is nonexpansive. Then the mapping
is nonexpansive. Then the mapping  is demiclosed at zero, that is,
is demiclosed at zero, that is,  ,
,  implies
implies  .
.
Lemma 2.4 (see [16, Lemmas 3.1, 3.3]).
Let  be real smooth and strictly convex Banach space, and
be real smooth and strictly convex Banach space, and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  which is also a sunny nonexpansive retraction of
which is also a sunny nonexpansive retraction of  . Assume that
. Assume that  is a nonexpansive mapping and
is a nonexpansive mapping and  is a sunny nonexpansive retraction of
is a sunny nonexpansive retraction of  onto
onto  , then
, then  .
.
Lemma 2.5 (see [17, Lemma 2.2]).
Let  be a nonempty convex subset of a real
be a nonempty convex subset of a real  -uniformly smooth Banach space
-uniformly smooth Banach space  and
and  be a
be a  -strict pseudocontraction. For
-strict pseudocontraction. For  , we define
, we define  . Then, as
. Then, as  ,
,  ,
,  is nonexpansive such that
is nonexpansive such that  .
.
Lemma 2.6 (see [12, Remark 2.6]).
When  is non-self-mapping, the Lemma 2.5 also holds.
is non-self-mapping, the Lemma 2.5 also holds.
Lemma 2.7 (see [12, Lemma 2.8]).
Assume that  is a strongly positive linear bounded operator on a smooth Banach space
is a strongly positive linear bounded operator on a smooth Banach space  with coefficient
with coefficient  and
and  . Then,
. Then,

Lemma 2.8 (see [18, Lemma 2.3]).
Let  be an MKC on a convex subset
be an MKC on a convex subset  of a Banach space
of a Banach space  . Then for each
. Then for each  , there exists
, there exists  such that
such that

Lemma 2.9.
Let  be a closed convex subset of a reflexive Banach space
be a closed convex subset of a reflexive Banach space  which admits a weakly sequentially continuous duality mapping
which admits a weakly sequentially continuous duality mapping  from
from  to
to  . Let
. Let  be a nonexpansive mapping with
be a nonexpansive mapping with  and
and  be a MKC,
be a MKC,  is strongly positive linear bounded operator with coefficient
is strongly positive linear bounded operator with coefficient  . Assume that
. Assume that  . Then the sequence
. Then the sequence  define by
define by  converges strongly as
converges strongly as  to a fixed point
to a fixed point  of
of  which solves the variational inequality:
which solves the variational inequality:

Proof.
The definition of  is well definition. Indeed, from the definition of MKC, we can see MKC is also a nonexpansive mapping. Consider a mapping
is well definition. Indeed, from the definition of MKC, we can see MKC is also a nonexpansive mapping. Consider a mapping  on
on  defined by
defined by

It is easy to see that  is a contraction. Indeed, by Lemma 2.8, we have
is a contraction. Indeed, by Lemma 2.8, we have

Hence,  has a unique fixed point, denoted by
has a unique fixed point, denoted by  , which uniquely solves the fixed point equation
, which uniquely solves the fixed point equation

We next show the uniqueness of a solution of the variational inequality (2.3). Suppose both  and
and  are solutions to (2.3), not lost generality, we may assume there is a number
are solutions to (2.3), not lost generality, we may assume there is a number  such that
such that  . Then by Lemma 2.8, there is a number
. Then by Lemma 2.8, there is a number  such that
such that  . From (2.3), we know
. From (2.3), we know

Adding up (2.7) gets

Noticing that

Therefore  and the uniqueness is proved. Below, we use
and the uniqueness is proved. Below, we use  to denote the unique solution of (2.3).
to denote the unique solution of (2.3).
We observe that  is bounded. Indeed, we may assume, with no loss of generality,
is bounded. Indeed, we may assume, with no loss of generality,  , for all
, for all  , fixed
, fixed  , for each
, for each  .
.
Case 1 ( ).
).
In this case, we can see easily that  is bounded.
is bounded.
Case 2 ( ).
).
In this case, by Lemmas 2.7 and 2.8, there is a number  such that
such that

therefore,  . This implies the
. This implies the  is bounded.
is bounded.
To prove that  as
as  .
.
Since  is bounded and
is bounded and  is reflexive, there exists a subsequence
is reflexive, there exists a subsequence  of
of  such that
such that  . By
. By  . We have
. We have  , as
, as  . Since
. Since  satisfies Opial's condition, it follows from Lemma 2.3 that
satisfies Opial's condition, it follows from Lemma 2.3 that  . We claim
. We claim

By contradiction, there is a number  and a subsequence
and a subsequence  of
of  such that
such that  . From Lemma 2.8, there is a number
. From Lemma 2.8, there is a number  such that
such that  , we write
, we write

to derive that

It follows that

Therefore,

Using that the duality map  is single valued and weakly sequentially continuous from
is single valued and weakly sequentially continuous from  to
to  , by (2.15), we get that
, by (2.15), we get that  . It is a contradiction. Hence, we have
. It is a contradiction. Hence, we have  .
.
We next prove that  solves the variational inequality (2.3). Since
solves the variational inequality (2.3). Since

we derive that

Notice

It follows that, for  ,
,

Now replacing  in (2.19) with
in (2.19) with  and letting
and letting  , noticing
, noticing  for
for  , we obtain
, we obtain  . That is,
. That is,  is a solution of (2.3); Hence
is a solution of (2.3); Hence  by uniqueness. In a summary, we have shown that each cluster point of
by uniqueness. In a summary, we have shown that each cluster point of  (at
(at  ) equals
) equals  , therefore,
, therefore,  as
as  .
.
Lemma 2.10 . (see, e.g., Mitrinović [19, page 63]).
Let  . Then the following inequality holds:
. Then the following inequality holds:

for arbitrary positive real numbers  ,
,  .
.
Lemma 2.11.
Let  be a
be a  -uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping
-uniformly smooth Banach space which admits a weakly sequentially continuous duality mapping  from
from  to
to  and
and  be a nonempty convex subset of
be a nonempty convex subset of  . Assume that
. Assume that  is a countable family of
is a countable family of  -strict pseudocontraction for some
-strict pseudocontraction for some  and
and  such that
such that  . Assume that
. Assume that  is a positive sequence such that
is a positive sequence such that  . Then
. Then  is a
is a  -strict pseudocontraction with
-strict pseudocontraction with  and
and  .
.
Proof.
Let

and  . Then,
. Then,  is a
is a  -strict pseudocontraction with
-strict pseudocontraction with  . Indeed, we can firstly see the case of
. Indeed, we can firstly see the case of  .
.

which shows that  is a
is a  -strict pseudocontraction with
-strict pseudocontraction with  . By the same way, our proof method easily carries over to the general finite case.
. By the same way, our proof method easily carries over to the general finite case.
Next, we prove the infinite case. From the definition of  -strict pseudocontraction, we know
-strict pseudocontraction, we know

Hence, we can get

Taking  , from (2.24), we have
, from (2.24), we have

Consquently, for all  , if
, if  ,
,  and
and  , then
, then  strongly converges. Let
strongly converges. Let

we have

Hence,

So, we get  is
is  -strict pseudocontraction.
-strict pseudocontraction.
Finally, we show  . Suppose that
. Suppose that  , it is sufficient to show that
, it is sufficient to show that  . Indeed, for
. Indeed, for  , we have
, we have

where  . Hence,
. Hence,  for each
for each  , this means that
, this means that  .
.
3. Main Results
Lemma 3.1.
Let  be a real
be a real  -uniformly smooth, strictly convex Banach space and
-uniformly smooth, strictly convex Banach space and  be a closed convex subset of
be a closed convex subset of  such that
such that  . Let
. Let  be also a sunny nonexpansive retraction of
be also a sunny nonexpansive retraction of  . Let
. Let  be a MKC. Let
be a MKC. Let  be a strongly positive linear bounded operator with the coefficient
be a strongly positive linear bounded operator with the coefficient  such that
such that  and
and  be
be  -strictly pseudo-contractive non-self-mapping such that
-strictly pseudo-contractive non-self-mapping such that  . Let
. Let  . Let
. Let  be a sequence of
be a sequence of  generated by (1.12) with the sequences
generated by (1.12) with the sequences  ,
, and
and  in
in  , assume for each
, assume for each  ,
,  be an infinity sequence of positive number such that
be an infinity sequence of positive number such that  for all
for all  and
and  . The following control conditions are satisfied
. The following control conditions are satisfied
(i) ,
,
(ii) ,
,  for some
for some  and for all
and for all  ,
,
(iii) ,
,  ,
,
(iv) .
.
Then,  .
.
Proof.
Write, for each  ,
,  . By Lemma 2.11, each
. By Lemma 2.11, each  is a
is a  -strict pseudocontraction on
-strict pseudocontraction on  and
and  for all
for all  and the algorithm (1.12) can be rewritten as
and the algorithm (1.12) can be rewritten as

The rest of the proof will now be split into two parts.
Step 1.
First, we show that sequences  and
and  are bounded. Define a mapping
are bounded. Define a mapping

Then, from the control condition (ii), Lemmas 2.5 and 2.6, we obtain  is nonexpansive. Taking a point
is nonexpansive. Taking a point  , by Lemma 2.4, we can get
, by Lemma 2.4, we can get  . Hence, we have
. Hence, we have

From definition of MKC and Lemma 2.8, for each  there is a number
there is a number  , if
, if  then
then  ; If
; If  then
then  . It follow (3.1)
. It follow (3.1)

By induction, we have

which gives that the sequence  is bounded, so are
is bounded, so are  and
and  .
.
Step 2.
In this part, we shall claim that  , as
, as  . From (3.1), we get
. From (3.1), we get

Define

where

It follows that

which yields that

Next, we estimate  . Notice that
. Notice that

Substituting (3.11) into (3.10), we have

Hence, we have

Observing conditions (i), (iii), (iv), and the boundedness of  ,
,  ,
,  ,
,  ,
,  it follows that
it follows that

Thus by Lemma 2.1, we have  .
.
From (3.7), we have

Therefore,

Theorem 3.2.
Let  be a real
be a real  -uniformly smooth, strictly convex Banach space which admits a weakly sequentially continuous duality mapping
-uniformly smooth, strictly convex Banach space which admits a weakly sequentially continuous duality mapping  from
from  to
to  and
and  be a closed convex subset of
be a closed convex subset of  which be also a sunny nonexpansive retraction of
which be also a sunny nonexpansive retraction of  such that
such that  . Let
. Let  be a MKC. Let
be a MKC. Let  be a strongly positive linear bounded operator with the coefficient
be a strongly positive linear bounded operator with the coefficient  such that
such that  and
and  be
be  -strictly pseudo-contractive non-self-mapping such that
-strictly pseudo-contractive non-self-mapping such that  . Let
. Let  . Let
. Let  be a sequence of
be a sequence of  generated by (1.12) with the sequences
generated by (1.12) with the sequences  ,
, and
and  in
in  , assume for each
, assume for each  ,
,  for all
for all  and
and  for all
for all  . They satisfy the conditions (i), (ii), (iii), (iv) of Lemma 3.1 and (v)
. They satisfy the conditions (i), (ii), (iii), (iv) of Lemma 3.1 and (v)  and
and  . Then
. Then  converges strongly to
converges strongly to  , which also solves the following variational inequality
, which also solves the following variational inequality

Proof.
From (3.1), we obtain

So  , which together with the condition (i), (iv) and Lemma 3.1 implies
, which together with the condition (i), (iv) and Lemma 3.1 implies

Define  , then
, then  is a
is a  -strict pseudocontraction such that
-strict pseudocontraction such that  by Lemma 2.11, furthermore
by Lemma 2.11, furthermore  as
as  for all
for all  . Defines
. Defines  by
by

Then,  is nonexpansive with
is nonexpansive with  by Lemma 2.5. It follows from Lemma 2.4 that
by Lemma 2.5. It follows from Lemma 2.4 that  . Notice that
. Notice that

which combines with (3.19) yielding that

Next, we show that

where  with
with  being the fixed point of the contraction
being the fixed point of the contraction

To see this, we take a subsequence  of
of  such that
such that

We may also assume that  . Note that
. Note that  in virtue of Lemma 2.3 and (3.22). It follow from the Lemma 2.9 and
in virtue of Lemma 2.3 and (3.22). It follow from the Lemma 2.9 and  is weak weakly sequentially continuous duality mapping that
is weak weakly sequentially continuous duality mapping that

Hence, we have

Finally, We show  . By contradiction, there is a number
. By contradiction, there is a number  such that
such that

Case 1.
Fixed  (
( ), if for some
), if for some  such that
such that  , and for the other
, and for the other  such that
such that  .
.
Let

From (3.23), we know  . Hence, there is a number
. Hence, there is a number  , when
, when  , we have
, we have  . We extract a number
. We extract a number  stastifying
stastifying  , then we estimate
, then we estimate  .
.

which implies that

Hence, we have

In the same way, we can get

It contradict the  .
.
Case 2.
Fixed  (
( ), if
), if  for all
for all  , from Lemma 2.8, there is a number
, from Lemma 2.8, there is a number  ,
,  such that
such that

It follow (3.1) that

which implies that

Apply Lemma 2.2 to (3.36) to conclude  as
as  . It contradict the
. It contradict the  . This completes the proof.
. This completes the proof.
Corollary 3.3.
Let  be a closed convex subset of a Hilbert space
be a closed convex subset of a Hilbert space  such that
such that  and
and  with the coefficient
with the coefficient  . Let
. Let  be a strongly positive linear bounded operator with the coefficient
be a strongly positive linear bounded operator with the coefficient  such that
such that  and
and  be
be  -strictly pseudo-contractive non-self-mapping such that
-strictly pseudo-contractive non-self-mapping such that  . Let
. Let  . Let
. Let  be a sequence of
be a sequence of  generated by (1.12) with the sequences
generated by (1.12) with the sequences  ,
,  , and
, and  in
in  , assume for each
, assume for each  ,
,  for all
for all  and
and  for all
for all  . They satisfy the conditions (i), (ii), (iii), (iv) of Lemma 3.1 and (v)
. They satisfy the conditions (i), (ii), (iii), (iv) of Lemma 3.1 and (v)  ,
,  and
and  . Then
. Then  converges strongly to
converges strongly to  , which also solves the following variational inequality
, which also solves the following variational inequality

Remark 3.4.
We conclude the paper with the following observations.
(i)Theorem 3.2 improve and extends Theorem 3.1 of Zhang and Su [17], Theorem 1 of Yao et al. [11], and Theorem 2.2 of Cai and Hu [12]. Corollary 3.3 also improve and extend Theorem 2.1 of Choa et al. [20], Theorem 2.1 of Jung [21], Theorem 2.1 of Qin et al. [22] and includes those results as special cases. Especially, Our results extends above results form contractions to more general Meir-Keeler contraction (MKC, for short). Our iterative scheme studied in present paper can be viewed as a refinement and modification of the iterative methods in [12, 13, 17, 22]. On the other hand, our iterative schemes concern an infinite countable family of  -strict pseudocontractions mappings, in this respect, they can be viewed as an another improvement.
-strict pseudocontractions mappings, in this respect, they can be viewed as an another improvement.
(ii)The advantage of the results in this paper is that less restrictions on the parameters  ,
,  ,
,  and
and  are imposed. Our results unify many recent results including the results in [12, 17, 22].
are imposed. Our results unify many recent results including the results in [12, 17, 22].
(iii)It is worth noting that we obtained two strong convergence results concerning an infinite countable family of  -strict pseudocontractions mappings. Our result is new and the proofs are simple and different from those in [11, 12, 17, 19–25].
-strict pseudocontractions mappings. Our result is new and the proofs are simple and different from those in [11, 12, 17, 19–25].
References
Browder FE: Convergence theorems for sequences of nonlinear operators in Banach spaces. Mathematische Zeitschrift 1967, 100: 201–225. 10.1007/BF01109805
Gossez J-P, Lami Dozo E: Some geometric properties related to the fixed point theory for nonexpansive mappings. Pacific Journal of Mathematics 1972, 40: 565–573.
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Banach S: Surles ope'rations dans les ensembles abstraits et leur application aux e'quations inte'grales. Fundamenta Mathematicae 1922, 3: 133–181.
Meir A, Keeler E: A theorem on contraction mappings. Journal of Mathematical Analysis and Applications 1969, 28: 326–329. 10.1016/0022-247X(69)90031-6
Kim T-H, Xu H-K: Strong convergence of modified Mann iterations. Nonlinear Analysis. Theory, Methods & Applications 2005,61(1–2):51–60. 10.1016/j.na.2004.11.011
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. Journal of Mathematical Analysis and Applications 2003,279(2):372–379. 10.1016/S0022-247X(02)00458-4
Zhou H: Convergence theorems of fixed points for κ -strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis, Theory, Methods and Applications 2008,69(2):456–462. 10.1016/j.na.2007.05.032
Qin X, Su Y: Approximation of a zero point of accretive operator in Banach spaces. Journal of Mathematical Analysis and Applications 2007,329(1):415–424. 10.1016/j.jmaa.2006.06.067
Marino G, Xu Hong-Kun: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,329(1):336–346. 10.1016/j.jmaa.2006.06.055
Yao Y, Chen R, Yao J-C: Strong convergence and certain control conditions for modified Mann iteration. Nonlinear Analysis, Theory, Methods and Applications 2008,68(6):1687–1693. 10.1016/j.na.2007.01.009
Cai G, Hu CS: Strong convergence theorems of a general iterative process for a finite family of -strict pseudo-contractions in -uniformly smooth Banach spaces. Computers & Mathematics with Applications 2010,59(1):149–160. 10.1016/j.camwa.2009.07.068
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Jung JS: Iterative approaches to common fixed points of nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2005,302(2):509–520. 10.1016/j.jmaa.2004.08.022
Matsushita S-Y, Takahashi W: Strong convergence theorems for nonexpansive nonself-mappings without boundary conditions. Nonlinear Analysis. Theory, Methods & Applications 2008,68(2):412–419. 10.1016/j.na.2006.11.007
Zhang H, Su Y: Strong convergence theorems for strict pseudo-contractions in -uniformly smooth Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,70(9):3236–3242. 10.1016/j.na.2008.04.030
Suzuki T: Moudafi's viscosity approximations with Meir-Keeler contractions. Journal of Mathematical Analysis and Applications 2007,325(1):342–352. 10.1016/j.jmaa.2006.01.080
Mitrinović DS: Analytic Inequalities. Springer, New York, NY, USA; 1970:xii+400.
Cho YJ, Kang SM, Qin X: Some results on -strictly pseudo-contractive mappings in Hilbert spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,70(5):1956–1964. 10.1016/j.na.2008.02.094
Jung JS: Strong convergence of iterative methods for -strictly pseudo-contractive mappings in Hilbert spaces. Applied Mathematics and Computation 2010,215(10):3746–3753. 10.1016/j.amc.2009.11.015
Qin X, Shang M, Kang SM: Strong convergence theorems of modified Mann iterative process for strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,70(3):1257–1264. 10.1016/j.na.2008.02.009
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006,318(1):43–52. 10.1016/j.jmaa.2005.05.028
Zhou H: Convergence theorems of fixed points for Lipschitz pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2008,343(1):546–556. 10.1016/j.jmaa.2008.01.045
Acknowledgments
The authors are extremely grateful to the referee and the editor for their useful comments and suggestions which helped to improve this paper. This work was supported by the National Science Foundation of China under Grant (no. 10771175).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Song, Y., Hu, C. Strong Convergence Theorems of a New General Iterative Process with Meir-Keeler Contractions for a Countable Family of 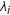 -Strict Pseudocontractions in
-Strict Pseudocontractions in 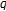 -Uniformly Smooth Banach Spaces.
Fixed Point Theory Appl 2010, 354202 (2010). https://doi.org/10.1155/2010/354202
-Uniformly Smooth Banach Spaces.
Fixed Point Theory Appl 2010, 354202 (2010). https://doi.org/10.1155/2010/354202
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/354202