- Research Article
- Open access
- Published:
Properties  and
and 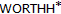 ,
,  Embeddings in Banach Spaces with 1-Unconditional Basis and
Embeddings in Banach Spaces with 1-Unconditional Basis and 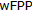
Fixed Point Theory and Applications volume 2010, Article number: 342691 (2009)
Abstract
We will use García-Falset and Lloréns Fuster's paper on the AMC-property to prove that a Banach space  that
that  embeds in a subspace
embeds in a subspace  of a Banach space
of a Banach space  with a 1-unconditional basis has the property AMC and thus the weak fixed point property. We will apply this to some results by Cowell and Kalton to prove that every reflexive real Banach space with the property
with a 1-unconditional basis has the property AMC and thus the weak fixed point property. We will apply this to some results by Cowell and Kalton to prove that every reflexive real Banach space with the property  and its dual have the
and its dual have the  and that a real Banach space
and that a real Banach space  such that
such that  is
is  sequentially compact and
sequentially compact and  has
has  has the
has the  .
.
1. Introduction
In 1988 Sims [1] introduced the notion of weak orthogonality  and asked whether spaces with WORTH have the weak fixed point property
and asked whether spaces with WORTH have the weak fixed point property  . Since then several partial answers have been given. For instance, in 1993 García-Falset [2] proved that if
. Since then several partial answers have been given. For instance, in 1993 García-Falset [2] proved that if  is uniformly nonsquare and has WORTH then it has the
is uniformly nonsquare and has WORTH then it has the  , although Mazcuñán Navarro in her doctoral dissertation [3] showed that uniform nonsquareness is enough. In this work she also showed that WORTH plus 2-UNC implies the
, although Mazcuñán Navarro in her doctoral dissertation [3] showed that uniform nonsquareness is enough. In this work she also showed that WORTH plus 2-UNC implies the  In both of these cases the space
In both of these cases the space  turns out to be reflexive. In 1994 Sims [4] himself proved that WORTH plus
turns out to be reflexive. In 1994 Sims [4] himself proved that WORTH plus  -inquadrate in every direction for some
-inquadrate in every direction for some  implies the
implies the  and in 2003 Dalby [5] showed that if
and in 2003 Dalby [5] showed that if  has
has  and is
and is  -inquadrate in every direction for some
-inquadrate in every direction for some  , then
, then  has the
has the  .
.
Recently in 2008 Cowell and Kalton [6] studied properties  and
and  in a Banach space
in a Banach space  , where
, where  coincides with WORTH if
coincides with WORTH if  is separable and
is separable and  in
in  coincides with
coincides with  in
in  if
if  is a separable Banach space. Among other things they proved that a real Banach space with
is a separable Banach space. Among other things they proved that a real Banach space with  embeds almost isometrically in a space with a shrinking 1-unconditional basis and observed that
embeds almost isometrically in a space with a shrinking 1-unconditional basis and observed that  and
and  are equivalent if
are equivalent if  is reflexive.
is reflexive.
We proved, using property AMC shown by García-Falset and Lloréns Fuster [7] to imply the  , that spaces that
, that spaces that  embed in a space with a 1-unconditional basis have the
embed in a space with a 1-unconditional basis have the  Combining this with Cowell and Kalton's results we were able to show that a reflexive real Banach space with WORTH and its dual both have
Combining this with Cowell and Kalton's results we were able to show that a reflexive real Banach space with WORTH and its dual both have  , giving a partial answer to Sims' question. We also showed that a separable space
, giving a partial answer to Sims' question. We also showed that a separable space  such that
such that  has
has  and
and  is
is  sequentially compact has the
sequentially compact has the  .
.
2. Notations and Definitions
Let  be a real Banach space and
be a real Banach space and  a closed nonempty bounded convex subset of
a closed nonempty bounded convex subset of  .
.
Definition 2.1.
If  , we define
, we define

If  the set of quasi-midpoints of
the set of quasi-midpoints of  and
and  in
in  is given by
is given by

Definition 2.2.
 is the quotient space
is the quotient space  endowed with the norm
endowed with the norm  where
where  is the equivalence class of
is the equivalence class of  in
in  , which we also will denote by
, which we also will denote by  . For
. For  we will also denote by
we will also denote by  the equivalence class
the equivalence class  in
in  . If
. If  is as above, let
is as above, let  . If
. If  is a Banach space and
is a Banach space and  for
for  we define
we define  ,
,  by
by

If  for
for  we denote
we denote  by
by  .
.
It is known that  is also closed bounded and convex in
is also closed bounded and convex in  and that
and that  .
.
Definition 2.3.
Let  be the set of strictly increasing sequences of natural numbers and
be the set of strictly increasing sequences of natural numbers and  a nonempty bounded convex subset of a Banach space
a nonempty bounded convex subset of a Banach space  . A sequence
. A sequence  in
in  is called equilateral in
is called equilateral in  , if for every
, if for every  such that
such that  for every
for every  , the following equality holds in
, the following equality holds in  . If
. If  and
and  , then
, then

where  .
.
It is easy to see that if  is equilateral in
is equilateral in  , and
, and  are as above, then
are as above, then

Now we define the property which interests us in this paper, it was given by García-Falset and Lloréns Fuster in 1990 [7].
Definition 2.4.
A bounded closed convex subset  of a Banach space
of a Banach space  with
with  has the AMC property, if for every weakly null sequence
has the AMC property, if for every weakly null sequence  which is equilateral in
which is equilateral in  , there exist
, there exist  ,
,  ,
,  with
with  for every
for every  , such that the set
, such that the set

is nonempty and  .
.  is said to have AMC if every weakly compact nonempty subset
is said to have AMC if every weakly compact nonempty subset  of
of  with
with  has the AMC property.
has the AMC property.
3. Embeddings into Spaces with 1-Unconditional Basis and the wFPP
Lin in [8] showed that if  has an unconditional basis
has an unconditional basis  with unconditional constant
with unconditional constant  , then
, then  has the
has the  . García-Falset and Lloréns Fuster proved that in fact under these conditions
. García-Falset and Lloréns Fuster proved that in fact under these conditions  has the AMC property which in turn implies the
has the AMC property which in turn implies the  . We will follow the proof of this closely to establish the next theorem.
. We will follow the proof of this closely to establish the next theorem.
Theorem 3.1.
Let  be a Banach space and suppose that there exists a Banach space
be a Banach space and suppose that there exists a Banach space  with a
with a  -unconditional basis
-unconditional basis  and a subspace
and a subspace  of
of  such that
such that  where
where  . Then
. Then  has AMC and thus the
has AMC and thus the  .
.
Proof.
Let  be an isomorphism with
be an isomorphism with  and
and  . Let
. Let  be a nonempty weakly compact convex subset of
be a nonempty weakly compact convex subset of  with
with  and
and  . We will show that
. We will show that  has the AMC property.
has the AMC property.
Let  be a weakly null equilateral sequence in
be a weakly null equilateral sequence in  and let
and let  . Then
. Then  is weakly compact and
is weakly compact and  is weakly null in
is weakly null in  . Hence there exists a sequence
. Hence there exists a sequence  and projections with respect to the basis
and projections with respect to the basis  in
in  with
with
(a) where
where  ,
,
(b) for all
for all  ,
,
(c) .
.
Let  be given by
be given by  . Then clearly
. Then clearly  for every
for every  . Let
. Let  be given by
be given by  and
and  and let
and let  be
be  . Recall that we will write
. Recall that we will write  instead of
instead of  . By (a), (b), and (c) and since
. By (a), (b), and (c) and since  is equilateral we have that
is equilateral we have that
(1) ,
,  and
and  ,
,
(2) ,
,  ,
,
(3) ,
,  ,
,
(4)for all  ,
,  .
.
Therefore, since  is
is  -unconditional
-unconditional

Thus  . Since by hypothesis
. Since by hypothesis  , we obtain that
, we obtain that  if
if  and
and  . Next we will show that
. Next we will show that  .
.
To this effect let  . Define
. Define  and
and  . Then for every
. Then for every 

By the unconditionality of  and since by (4) we have that
and since by (4) we have that  ,
,

Therefore

Now let  be such that
be such that  . Such an element exists since
. Such an element exists since  . Recalling that
. Recalling that  , we obtain that
, we obtain that

Using again that  , we get
, we get

or equivalently

On the other hand, since by (2)  , we have
, we have

Similarly

By (3.8) and (3.9), and (3.5) we obtain

Hence

Finally, from (3.7) and (3.11) we have  and
and

Therefore, if  we conclude that
we conclude that  and thus
and thus  has the AMC property.
has the AMC property.
Remark 3.2.
It is evident that if the space  has a
has a  unconditional basis, if
unconditional basis, if  is small enough, the above result remains true for some
is small enough, the above result remains true for some  .
.
4. Some Consequences
There has always been the conjecture that a space with property WORTH has the  . We show here that this is correct as long as
. We show here that this is correct as long as  is reflexive. We also show that property
is reflexive. We also show that property  in
in  implies the
implies the  in Banach spaces
in Banach spaces  so that
so that  is
is  sequentially compact and that WORTH together with WABS implies the
sequentially compact and that WORTH together with WABS implies the  as well. All these results are consequences of some theorems by Cowell and Kalton [6]. First we need to recall some definitions.
as well. All these results are consequences of some theorems by Cowell and Kalton [6]. First we need to recall some definitions.
Definition 4.1.
A Banach space  has the WORTH property if for every weakly null sequence
has the WORTH property if for every weakly null sequence  and every
and every  , the following equality holds:
, the following equality holds:

This definition was given by Sims in [1]. The next definition was stated by Dalby [5].
Definition 4.2.
A Banach space  has the
has the  property if for every weak
property if for every weak null sequence
null sequence  and every
and every  , the following equality holds:
, the following equality holds:

If  is separable and
is separable and  has
has  , this coincides with the property
, this coincides with the property  defined in [6].
defined in [6].
Definition 4.3.
A Banach space  has the Weak Alternating Banach-Saks (WABS) property if every bounded sequence
has the Weak Alternating Banach-Saks (WABS) property if every bounded sequence  in
in  has a convex block sequence
has a convex block sequence  such that
such that

Cowell and Kalton in [6] proved the following three results.
Theorem 4.4.
If  is a separable real Banach space, then
is a separable real Banach space, then  has the property
has the property  if and only if for any
if and only if for any  there is a Banach space
there is a Banach space  with a shrinking
with a shrinking  -unconditional basis and a subspace
-unconditional basis and a subspace  of
of  such that
such that  .
.
Dalby [5] observed that property  in a space
in a space  implies property WORTH in
implies property WORTH in  and it follows that if
and it follows that if  is reflexive, then both properties are equivalent. From this and another theorem we are not going to mention here, Cowell and Kalton obtained the next theorem.
is reflexive, then both properties are equivalent. From this and another theorem we are not going to mention here, Cowell and Kalton obtained the next theorem.
Theorem 4.5.
If  is a separable real reflexive space, then
is a separable real reflexive space, then  has property WORTH if and only if for any
has property WORTH if and only if for any  there is a reflexive Banach space
there is a reflexive Banach space  with a
with a  -unconditional basis and a subspace
-unconditional basis and a subspace  of
of  such that
such that  .
.
The third result we are going to use is as follows.
Theorem 4.6.
If  is a separable real Banach space, then
is a separable real Banach space, then  has both the properties
has both the properties  and WABS if and only if for any
and WABS if and only if for any  there is a Banach space
there is a Banach space  with a shrinking
with a shrinking  -unconditional basis and a subspace
-unconditional basis and a subspace  of
of  such that
such that  .
.
From this and our previous work it follows directly the following:
Theorem 4.7.
If  is a real separable space such that either
is a real separable space such that either
(I) has property
has property  ,
,
(II) is reflexive and has property WORTH, or
is reflexive and has property WORTH, or
(III) has both the properties WORTH and WABS,
has both the properties WORTH and WABS,
then  has the property AMC and thus the
has the property AMC and thus the  .
.
It is known that reflexivity implies WABS, and thus (II) implies (III), but we want to include (II) in order to deduce the next corollary. Properties  and WABS are inherited by subspaces, and if
and WABS are inherited by subspaces, and if  has property
has property  and
and  is
is  sequentially compact, then the dual of any subspace of
sequentially compact, then the dual of any subspace of  also has this property. Hence we have the following result.
also has this property. Hence we have the following result.
Corollary 4.8.
Let  be a real Banach space.
be a real Banach space.
(1)If  is reflexive and has property
is reflexive and has property  , then
, then  and
and  both have the
both have the  .
.
(2)If  has properties WORTH and WABS, then
has properties WORTH and WABS, then  has the
has the  .
.
(3)If  has
has  and
and  is
is  sequentially compact, then
sequentially compact, then  has the
has the  .
.
Proof.
If  is a Banach space that satisfies (1), (2), or (3), every separable subspace has the
is a Banach space that satisfies (1), (2), or (3), every separable subspace has the  and hence, since the
and hence, since the  is separably determined,
is separably determined,  has the
has the  . If
. If  is separable and reflexive and has property
is separable and reflexive and has property  , then it has property
, then it has property  as well and this implies by definition that
as well and this implies by definition that  also has property
also has property  . Therefore both have the
. Therefore both have the  and hence the result follows for nonseparable reflexive spaces.
and hence the result follows for nonseparable reflexive spaces.
References
Sims B: Orthogonality and fixed points of nonexpansive maps. In Workshop/Miniconference on Functional Analysis and Optimization (Canberra, 1988), Proceedings of the Centre for Mathematical Analysis, Australian National University. Volume 20. The Australian National University, Canberra, Australia; 1988:178–186.
García-Falset J: The fixed point property in Banach spaces whose characteristic of uniform convexity is less than 2. Journal of the Australian Mathematical Society. Series A 1993,54(2):169–173. 10.1017/S1446788700037095
Mazcuñán Navarro EM: Geometría de los espacios de Banach en teoría métrica del punto fijo, Tesis doctoral. Universitat de Valencia, Valencia, Spain; 2003.
Sims B: A class of spaces with weak normal structure. Bulletin of the Australian Mathematical Society 1994,49(3):523–528. 10.1017/S0004972700016634
Dalby T: The effect of the dual on a Banach space and the weak fixed point property. Bulletin of the Australian Mathematical Society 2003,67(2):177–185. 10.1017/S0004972700033657
Cowell SR, Kalton NJ: Asymptotic unconditionality. http://arxiv.org/abs/0809.2294
García-Falset J, Lloréns Fuster E: A geometric property of Banach spaces related to the fixed point property. Journal of Mathematical Analysis and Applications 1993,172(1):39–52. 10.1006/jmaa.1993.1005
Lin P-K: Unconditional bases and fixed points of nonexpansive mappings. Pacific Journal of Mathematics 1985,116(1):69–76.
Acknowledgment
This work is partially supported by SEP-CONACYT Grant 102380. It is dedicated to W. A. Kirk.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fetter, H., Gamboa de Buen, B. Properties  and
and 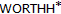 ,
,  Embeddings in Banach Spaces with 1-Unconditional Basis and
Embeddings in Banach Spaces with 1-Unconditional Basis and 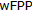 .
Fixed Point Theory Appl 2010, 342691 (2009). https://doi.org/10.1155/2010/342691
.
Fixed Point Theory Appl 2010, 342691 (2009). https://doi.org/10.1155/2010/342691
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/342691