- Research Article
- Open access
- Published:
Convergence Theorems for the Unique Common Fixed Point of a Pair of Asymptotically Nonexpansive Mappings in Generalized Convex Metric Space
Fixed Point Theory and Applications volume 2010, Article number: 281890 (2010)
Abstract
Let  be a generalized convex metric space, and let
be a generalized convex metric space, and let  ,
,  be a pair of asymptotically nonexpansive mappings. In this paper, we will consider an Ishikawa type iteration process with errors to approximate the unique common fixed point of
be a pair of asymptotically nonexpansive mappings. In this paper, we will consider an Ishikawa type iteration process with errors to approximate the unique common fixed point of  and
and  .
.
1. Introduction and Preliminaries
Let  be a metric space,
be a metric space,  a pair of asymptotically nonexpansive mappings if there exists
a pair of asymptotically nonexpansive mappings if there exists  such that
such that

for all  ,
,  .
.
Bose [1] first defined a pair of mean nonexpansive mappings in Banach space, that is,

(let  in (*)), and then they proved several convergence theorems for commom fixed points of mean nonexpansive mappings. Gu and Li [2] also studied the same problem; they considered the Ishikawa iteration process to approximate the common fixed point of mean nonexpansive mappings in uniformly convex Banach space. Takahashi [3] first introduced a notion of convex metric space, which is more general space, and each linear normed space is a special example of the space. Late on, Ciric et al.[4] proved the convergence of an Ishikawa type iteration process to approximate the common fixed point of a pair of mappings (under condition (B), which is also a special example of (*)) in convex metric space. Very recently, Wang and Liu [5] give some sufficiency and necessary conditions for an Ishikawa type iteration process with errors to approximate a common fixed point of two mappings in generalized convex metric space.
in (*)), and then they proved several convergence theorems for commom fixed points of mean nonexpansive mappings. Gu and Li [2] also studied the same problem; they considered the Ishikawa iteration process to approximate the common fixed point of mean nonexpansive mappings in uniformly convex Banach space. Takahashi [3] first introduced a notion of convex metric space, which is more general space, and each linear normed space is a special example of the space. Late on, Ciric et al.[4] proved the convergence of an Ishikawa type iteration process to approximate the common fixed point of a pair of mappings (under condition (B), which is also a special example of (*)) in convex metric space. Very recently, Wang and Liu [5] give some sufficiency and necessary conditions for an Ishikawa type iteration process with errors to approximate a common fixed point of two mappings in generalized convex metric space.
Inspired and motivated by the above facts,we will consider the Ishikawa type iteration process with errors, which converges to the unique common fixed point of the pair of asymptotically nonexpansive mappings in generalized convex metric space. Our results extend and improve the corresponding results in [1–6].
First of all, we will need the following definitions and conclusions.
Definition 1.1 (see [3]).
Let  be a metric space, and
be a metric space, and  . A mapping
. A mapping  is said to be convex structure on
is said to be convex structure on  , if for any
, if for any  and
and  , the following inequality holds:
, the following inequality holds:

If  is a metric space with a convex structure
is a metric space with a convex structure  , then
, then  is called a convex metric space. Moreover, a nonempty subset
is called a convex metric space. Moreover, a nonempty subset  of
of  is said to be convex if
is said to be convex if  , for all
, for all  .
.
Definition 1.2 (see [6]).
Let  be a metric space,
be a metric space,  , and
, and  real sequences in
real sequences in  with
with  . A mapping
. A mapping  is said to be convex structure on
is said to be convex structure on  , if for any
, if for any  and
and  , the following inequality holds:
, the following inequality holds:

If  is a metric space with a convex structure
is a metric space with a convex structure  , then
, then  is called a generalized convex metric space. Moreover, a nonempty subset
is called a generalized convex metric space. Moreover, a nonempty subset  of
of  is said to be convex if
is said to be convex if  , for all
, for all  .
.
Remark 1.3.
It is easy to see that every generalized convex metric space is a convex metric space (let  ).
).
Definition 1.4.
Let  be a generalized convex metric space with a convex structure
be a generalized convex metric space with a convex structure  , and
, and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be a pair of asymptotically nonexpansive mappings, and
be a pair of asymptotically nonexpansive mappings, and  six sequences in
six sequences in  with
with  for any given
for any given  , define a sequence
, define a sequence  as follows:
as follows:

where  are two sequences in
are two sequences in  satisfying the following condition. If for any nonnegative integers
satisfying the following condition. If for any nonnegative integers  ,
,  , then
, then

where  ,
,

then  is called the Ishikawa type iteration process with errors of a pair of asymptotically nonexpansive mappings S and T.
is called the Ishikawa type iteration process with errors of a pair of asymptotically nonexpansive mappings S and T.
Remark 1.5.
Note that the iteration processes considered in [1, 2, 4, 6] can be obtained from the above process as special cases by suitably choosing the space, the mappings, and the parameters.
Theorem 1.6 (see [5]).
Let  be a nonempty closed convex subset of complete convex metric space
be a nonempty closed convex subset of complete convex metric space  , and
, and  uniformly quasi-Lipschitzian mappings with
uniformly quasi-Lipschitzian mappings with  and
and  , and
, and  (
( ). Suppose that
). Suppose that  is the Ishikawa type iteration process with errors defined by (1.4),
is the Ishikawa type iteration process with errors defined by (1.4),  satisfy (**), and
satisfy (**), and  are six sequences in
are six sequences in  satisfying
satisfying

then  converge to a fixed point of
converge to a fixed point of  and
and  if and only if
if and only if  where
where  .
.
Remark 1.7.
Let  . A mapping
. A mapping  is called uniformly quasi-Lipshitzian if there exists
is called uniformly quasi-Lipshitzian if there exists  such that
such that

for all  ,
,  .
.
2. Main Results
Now, we will prove the strong convergence of the iteration scheme (1.4) to the unique common fixed point of a pair of asymptotically nonexpansive mappings  and
and  in complete generalized convex metric spaces.
in complete generalized convex metric spaces.
Theorem 2.1.
Let  be a nonempty closed convex subset of complete generalized convex metric space
be a nonempty closed convex subset of complete generalized convex metric space  , and
, and  a pair of asymptotically nonexpansive mappings with
a pair of asymptotically nonexpansive mappings with  , and
, and  . Suppose
. Suppose  as in (1.4),
as in (1.4),  satisfy (**), and
satisfy (**), and  are six sequences in
are six sequences in  satisfying
satisfying

then  converge to the unique common fixed point of
converge to the unique common fixed point of  and
and  if and only if
if and only if  where
where  .
.
Proof.
The necessity of conditions is obvious. Thus, we will only prove the sufficiency.
Let  , for all
, for all  ,
,

implies

which yield (using the fact that  and
and  )
)

where  . Similarly, we also have
. Similarly, we also have  .
.
By Remark 1.7, we get that  and
and  are two uniformly quasi-Lipschitzian mappings (with
are two uniformly quasi-Lipschitzian mappings (with  ). Therefore, from Theorem 1.6, we know that
). Therefore, from Theorem 1.6, we know that  converges to a common fixed point of
converges to a common fixed point of  and
and  .
.
Finally, we prove the uniqueness. Let  ,
,  , then, by (*), we have
, then, by (*), we have

Since  , we obtain
, we obtain  . This completes the proof.
. This completes the proof.
Remark 2.2.
-
(i)
We consider a sufficient and necessary condition for the Ishikawa type iteration process with errors in complete generalized convex metric space; our mappings are the more general mappings (a pair of asymptotically nonexpansive mappings), so our result extend and generalize the corresponding results in [1–4, 6].
-
(ii)
Since
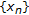 converges to the unique fixed point of
converges to the unique fixed point of  and
and  , we have improved Theorem 1.6 in [5].
, we have improved Theorem 1.6 in [5].
Corollary 2.3.
Let  be a nonempty closed convex subset of Banach space
be a nonempty closed convex subset of Banach space  ,
,  a pair of asymptotically nonexpansive mappings, that is,
a pair of asymptotically nonexpansive mappings, that is,

with  , and
, and  . For any given
. For any given  ,
,  is an Ishikawa type iteration process with errors defined by
is an Ishikawa type iteration process with errors defined by

where  are two bounded sequences and
are two bounded sequences and  are six sequences in
are six sequences in  satisfying
satisfying

Then,  converges to the unique common fixed point of
converges to the unique common fixed point of  and
and  if and only if
if and only if  , where
, where  .
.
Proof.
From the proof of Theorem 2.1, we have

where  . Hence,
. Hence,  and
and  are two uniformly quasi-Lipschitzian mappings in Banach space. Since Theorem 1.6 also holds in Banach spaces, we can prove that there exists a
are two uniformly quasi-Lipschitzian mappings in Banach space. Since Theorem 1.6 also holds in Banach spaces, we can prove that there exists a  such that
such that  . The proof of uniqueness is the same to that of Theorem 2.1. Therefore,
. The proof of uniqueness is the same to that of Theorem 2.1. Therefore,  converges to the unique common fixed point of
converges to the unique common fixed point of  and
and  .
.
Corollary 2.4.
Let  be a nonempty closed convex subset of Banach space
be a nonempty closed convex subset of Banach space  ,
,  a pair of asymptotically nonexpansive mappings, that is,
a pair of asymptotically nonexpansive mappings, that is,

with  , and
, and  . For any given
. For any given  ,
,  an Ishikawa type iteration process defined by
an Ishikawa type iteration process defined by

where  are two sequences in
are two sequences in  satisfying
satisfying  Then,
Then,  converges to the unique common fixed point of
converges to the unique common fixed point of  and
and  if and only if
if and only if  , where
, where  .
.
Proof.
Let  and
and  . The result can be deduced immediately from Corollary 2.3. This completes the proof.
. The result can be deduced immediately from Corollary 2.3. This completes the proof.
References
Bose SC: Common fixed points of mappings in a uniformly convex Banach space. Journal of the London Mathematical Society 1978,18(1):151–156. 10.1112/jlms/s2-18.1.151
Gu Z, Li Y: Approximation methods for common fixed points of mean nonexpansive mapping in Banach spaces. Fixed Point Theory and Applications 2008, 2008:-7.
Takahashi W: A convexity in metric space and nonexpansive mappings. I. Kodai Mathematical Seminar Reports 1970, 22: 142–149. 10.2996/kmj/1138846111
Ciric LB, Ume JS, Khan MS: On the convergence of the Ishikawa iterates to a common fixed point of two mappings. Archivum Mathematicum 2003,39(2):123–127.
Wang C, Liu LW: Convergence theorems for fixed points of uniformly quasi-Lipschitzian mappings in convex metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):2067–2071. 10.1016/j.na.2008.02.106
Tian Y-X: Convergence of an Ishikawa type iterative scheme for asymptotically quasi-nonexpansive mappings. Computers & Mathematics with Applications 2005,49(11–12):1905–1912. 10.1016/j.camwa.2004.05.017
Acknowledgments
The authors would like to thank the referee and the editor for their careful reading of the manuscript and their many valuable comments and suggestions. The research was supported by the Natural Science Foundation of China (no. 70432001) and Shanghai Leading Academic Discipline Project (B210).
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, C., Li, J. & Zhu, D. Convergence Theorems for the Unique Common Fixed Point of a Pair of Asymptotically Nonexpansive Mappings in Generalized Convex Metric Space. Fixed Point Theory Appl 2010, 281890 (2010). https://doi.org/10.1155/2010/281890
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/281890
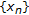 converges to the unique fixed point of
converges to the unique fixed point of  and
and  , we have improved Theorem 1.6 in [
, we have improved Theorem 1.6 in [