- Research Article
- Open access
- Published:
The Szlenk Index and the Fixed Point Property under Renorming
Fixed Point Theory and Applications volume 2010, Article number: 268270 (2010)
Abstract
Assume that  is a Banach space such that its Szlenk index
is a Banach space such that its Szlenk index  is less than or equal to the first infinite ordinal
is less than or equal to the first infinite ordinal  . We prove that
. We prove that  can be renormed in such a way that
can be renormed in such a way that  with the resultant norm satisfies
with the resultant norm satisfies  , where
, where  is the García-Falset coefficient. This leads us to prove that if
is the García-Falset coefficient. This leads us to prove that if  is a Banach space which can be continuously embedded in a Banach space
is a Banach space which can be continuously embedded in a Banach space  with
with  , then,
, then,  can be renormed to satisfy the w-FPP. This result can be applied to Banach spaces which can be embedded in
can be renormed to satisfy the w-FPP. This result can be applied to Banach spaces which can be embedded in  , where
, where  is a scattered compact topological space such that
is a scattered compact topological space such that  . Furthermore, for a Banach space
. Furthermore, for a Banach space  , we consider a distance in the space
, we consider a distance in the space  of all norms in
of all norms in  which are equivalent to
which are equivalent to  (for which
(for which  becomes a Baire space). If
becomes a Baire space). If  , we show that for almost all norms (in the sense of porosity) in
, we show that for almost all norms (in the sense of porosity) in  ,
,  satisfies the w-FPP. For general reflexive spaces (independently of the Szlenk index), we prove another strong generic result in the sense of Baire category.
satisfies the w-FPP. For general reflexive spaces (independently of the Szlenk index), we prove another strong generic result in the sense of Baire category.
1. Introduction
Assume that  is a Banach space. The most common aim of the Renorming Theory is to find an equivalent norm which satisfies (or which does not satisfy) certain specific properties. A detailed account of this topic can be found in the monographs [1–3]. This paper focuses on the Renorming Theory in connection with the Fixed Point Theory. It is usually said that a Banach space
is a Banach space. The most common aim of the Renorming Theory is to find an equivalent norm which satisfies (or which does not satisfy) certain specific properties. A detailed account of this topic can be found in the monographs [1–3]. This paper focuses on the Renorming Theory in connection with the Fixed Point Theory. It is usually said that a Banach space  satisfies the weak Fixed Point Property (w-FPP) if for every convex weakly compact subset
satisfies the weak Fixed Point Property (w-FPP) if for every convex weakly compact subset  of
of  , each nonexpansive mapping
, each nonexpansive mapping  has a fixed point. Many geometrical properties of
has a fixed point. Many geometrical properties of  (uniform convexity, uniform smoothness, uniform convexity in every direction, uniform non-squareness, normal structure, etc.) are known to imply the w-FPP (see, e.g., [4–6] and references therein). However, no characterization of the w-FPP in terms of these properties is known. Therefore, we can regard the w-FPP as an intrinsic property of a Banach space. Since the w-FPP is not preserved under isomorphisms, a very natural question in Renorming Theory and Fixed Point Theory would be the following: let
(uniform convexity, uniform smoothness, uniform convexity in every direction, uniform non-squareness, normal structure, etc.) are known to imply the w-FPP (see, e.g., [4–6] and references therein). However, no characterization of the w-FPP in terms of these properties is known. Therefore, we can regard the w-FPP as an intrinsic property of a Banach space. Since the w-FPP is not preserved under isomorphisms, a very natural question in Renorming Theory and Fixed Point Theory would be the following: let  be a Banach space. Is it possible to renorm
be a Banach space. Is it possible to renorm  so that the resultant space has the w-FPP? This is not generally the case. Indeed, Partington [7, 8] has proved that every renorming of
so that the resultant space has the w-FPP? This is not generally the case. Indeed, Partington [7, 8] has proved that every renorming of  for an uncountable set
for an uncountable set  and any renorming of
and any renorming of  contains an isometric copy of
contains an isometric copy of  and, consequently, it fails the w-FPP (due to Alspach example [9]). Thus, it would be interesting to identify some classes of Banach spaces which can be renormed to satisfy the w-FPP. For instance, Day et al. [10] have proved that every separable Banach space has a UCED renorming. Since uniform convexity in every direction implies normal structure and this property implies the w-FPP (see, e.g., [4]), we obtain that any separable Banach space can be renormed to satisfy the w-FPP. These arguments do not work for nonseparable spaces because, as mentioned above, there are some Banach spaces which cannot be renormed to satisfy the w-FPP. (In fact, in [10], it is shown that
and, consequently, it fails the w-FPP (due to Alspach example [9]). Thus, it would be interesting to identify some classes of Banach spaces which can be renormed to satisfy the w-FPP. For instance, Day et al. [10] have proved that every separable Banach space has a UCED renorming. Since uniform convexity in every direction implies normal structure and this property implies the w-FPP (see, e.g., [4]), we obtain that any separable Banach space can be renormed to satisfy the w-FPP. These arguments do not work for nonseparable spaces because, as mentioned above, there are some Banach spaces which cannot be renormed to satisfy the w-FPP. (In fact, in [10], it is shown that  has no UCED renorming if
has no UCED renorming if  is uncountable). Since in [11] an example is given of a reflexive Banach spaces which does not admit any UCED renorming, the following question, which appears in [12, Open Question VI] and [1, Problem VII.3] and which remained unanswered for a long time, seems to be very natural: can any reflexive Banach space be renormed to satisfy the (w)-FPP? In [13] it is shown that this is indeed the case. Actually, the following result is proved in [13]: assume that
is uncountable). Since in [11] an example is given of a reflexive Banach spaces which does not admit any UCED renorming, the following question, which appears in [12, Open Question VI] and [1, Problem VII.3] and which remained unanswered for a long time, seems to be very natural: can any reflexive Banach space be renormed to satisfy the (w)-FPP? In [13] it is shown that this is indeed the case. Actually, the following result is proved in [13]: assume that  is a Banach space such that there exists a bounded one-one linear operator from
is a Banach space such that there exists a bounded one-one linear operator from  into
into  . Then,
. Then,  has an equivalent norm which satisfies the w-FPP. This embedding property is satisfied by a very general class of Banach spaces, for instance subspaces of a space with Markushevich basis, as WCG spaces (and so separable and reflexive spaces), dual of separable spaces as
has an equivalent norm which satisfies the w-FPP. This embedding property is satisfied by a very general class of Banach spaces, for instance subspaces of a space with Markushevich basis, as WCG spaces (and so separable and reflexive spaces), dual of separable spaces as  , and so forth.
, and so forth.
The proof of the result in [13] is strongly based upon some specific properties of the space  , specially the equality
, specially the equality  , where
, where  is García-Falset's coefficient [14]. It must be noted that any Banach space
is García-Falset's coefficient [14]. It must be noted that any Banach space  such that
such that  satisfies the w-FPP (see [15]). Thus, it would be natural to extend the above result to any Banach space which can be embedded in more general Banach spaces than
satisfies the w-FPP (see [15]). Thus, it would be natural to extend the above result to any Banach space which can be embedded in more general Banach spaces than  , but still satisfying
, but still satisfying  . In [16] we prove this extension in the following sense: assume that
. In [16] we prove this extension in the following sense: assume that  is a Banach space such that
is a Banach space such that  , where
, where  is García-Falset's coefficient, and
is García-Falset's coefficient, and  is a Banach space which can be continuously embedded in
is a Banach space which can be continuously embedded in  . Then,
. Then,  can be renormed to satisfy the w-FPP.
can be renormed to satisfy the w-FPP.
In this paper we will use the Szlenk index to show a wide class of Banach spaces  which can be renormed to satisfy
which can be renormed to satisfy  . The Szlenk index
. The Szlenk index  [17] is an ordinal number which was introduced to prove that there is no separable reflexive Banach space universal for the class of all separable reflexive Banach spaces. Later, this index has been used in various areas of the geometry of Banach spaces (see [18] for a survey about it). Recently, Raja [19] has proved that if
[17] is an ordinal number which was introduced to prove that there is no separable reflexive Banach space universal for the class of all separable reflexive Banach spaces. Later, this index has been used in various areas of the geometry of Banach spaces (see [18] for a survey about it). Recently, Raja [19] has proved that if  is an Asplund space and
is an Asplund space and  , then there is an equivalent norm on
, then there is an equivalent norm on  such that the dual norm on
such that the dual norm on  is UKK*. We will show in this paper that this fact leads us to prove
is UKK*. We will show in this paper that this fact leads us to prove  when
when  is endowed with this norm.
is endowed with this norm.
On the other hand, if we endow  with the discrete topology and denote by
with the discrete topology and denote by  the one-point compactification of
the one-point compactification of  , then
, then  is isometrically contained in
is isometrically contained in  , where
, where  is a topological compact space which satisfies
is a topological compact space which satisfies  . Thus, if a Banach space can be continuously embedded in
. Thus, if a Banach space can be continuously embedded in  then, it can also be embedded in
then, it can also be embedded in  , where
, where  is a scattered compact topological space such that
is a scattered compact topological space such that  . Since
. Since  satisfies the w-FPP [20] when
satisfies the w-FPP [20] when  is a scattered compact topological space
is a scattered compact topological space  such that
such that  , another natural question would be the following: assume that
, another natural question would be the following: assume that  is a Banach space which can be continuously embedded in
is a Banach space which can be continuously embedded in  for some
for some  as above. Can
as above. Can  be renormed to satisfy the w-FPP? Using the results about the Szlenk index and the main result in [16], we can prove that this is indeed the case. Nominally, since
be renormed to satisfy the w-FPP? Using the results about the Szlenk index and the main result in [16], we can prove that this is indeed the case. Nominally, since  if (and only if)
if (and only if)  is as above, we obtain the following: let
is as above, we obtain the following: let  be the space of real continuous functions defined on a scattered compact topological space
be the space of real continuous functions defined on a scattered compact topological space  such that
such that  . Then, it can be renormed in such a way that
. Then, it can be renormed in such a way that  (where
(where  is the new norm) and the dual norm is UKK*. In order to better understand the relevance of this result, note that in the metrizable case, if
is the new norm) and the dual norm is UKK*. In order to better understand the relevance of this result, note that in the metrizable case, if  , then
, then  is isomorphic to
is isomorphic to  and, consequently, there exists an equivalent norm
and, consequently, there exists an equivalent norm  such that
such that  . From this result and the main result in [16], we can easily deduce that if a Banach space can be continuously embedded in
. From this result and the main result in [16], we can easily deduce that if a Banach space can be continuously embedded in  ,
,  as above, then it can be renormed to satisfy the w-FPP. (In [16] the same result for
as above, then it can be renormed to satisfy the w-FPP. (In [16] the same result for  was obtained by a direct and very technical method). This is a strict improvement of the result in [13], because, as proved in [21], when
was obtained by a direct and very technical method). This is a strict improvement of the result in [13], because, as proved in [21], when  is a Ciesielski-Pol's compact, then
is a Ciesielski-Pol's compact, then  , but
, but  cannot be continuously embedded in
cannot be continuously embedded in  for any set
for any set  .
.
In the last section, for a Banach space  , we consider a metric in the space
, we consider a metric in the space  of all norms in
of all norms in  which are equivalent to
which are equivalent to  , and note that
, and note that  becomes a Baire space for the corresponding metric topology. If
becomes a Baire space for the corresponding metric topology. If  , we show that for almost all norms (in the sense of porosity) in
, we show that for almost all norms (in the sense of porosity) in  ,
,  satisfies the w-FPP. We finish with another strong generic result in the sense of Baire category for general reflexive spaces (without any assumption on the Szlenk index).
satisfies the w-FPP. We finish with another strong generic result in the sense of Baire category for general reflexive spaces (without any assumption on the Szlenk index).
2. Szlenk Index and Fixed Points
We start reminding some definition and stating the previous results which we will use.
Definition 2.1.
Let  be a topological space and
be a topological space and  a subset of
a subset of  . The set
. The set  is said to be perfect if it is closed and has no isolated point, that is,
is said to be perfect if it is closed and has no isolated point, that is,  is equal to the set of its own accumulation points. The space
is equal to the set of its own accumulation points. The space  is said to be scattered if it contains no perfect nonvoid subset.
is said to be scattered if it contains no perfect nonvoid subset.
If  is a subset of a topological space
is a subset of a topological space  , the derived set of
, the derived set of  is the set
is the set  of all accumulation points of
of all accumulation points of  . If
. If  is an ordinal number, we define the
is an ordinal number, we define the  th-derived set by transfinite induction:
th-derived set by transfinite induction:

where  is a limit ordinal.
is a limit ordinal.
Let us recall the definition of García-Falset's coefficient.
Definition 2.2 (see [14]).
Let  be a Banach space. The coefficient
be a Banach space. The coefficient  is defined by
is defined by

Theorem 2.3 (see [15]).
Let  be a Banach space such that
be a Banach space such that  . Then,
. Then,  satisfies the w-FPP.
satisfies the w-FPP.
Theorem 2.4 (see [16]).
Let  be a Banach space such that
be a Banach space such that  . Assume that
. Assume that  is another Banach space, such that there exists a continuous one-to-one mapping
is another Banach space, such that there exists a continuous one-to-one mapping  . Then,
. Then,  can be renormed to satisfy the w-FPP.
can be renormed to satisfy the w-FPP.
Definition 2.5.
Let  be a Banach space with dual
be a Banach space with dual  . We say that the dual norm is UKK* if for every
. We say that the dual norm is UKK* if for every  there is
there is  such that every
such that every  with
with  has a weak* open neighborhood
has a weak* open neighborhood  with diam
with diam  .
.
We remind the definition of the Szlenk index. Following the survey [18], we consider a more general definition than that in [17]. However, both definitions are identical for separable spaces which do not contain  .
.
Definition 2.6.
Let  be a Banach space and
be a Banach space and  its dual. For any bounded subset
its dual. For any bounded subset  , we define a Szlenk derivation by
, we define a Szlenk derivation by  : for every w*-neighborhood
: for every w*-neighborhood  of
of  , diam
, diam  . By iteration, the sets
. By iteration, the sets  are defined for any ordinal number
are defined for any ordinal number  , taking intersection in the case of limit ordinals. The indices
, taking intersection in the case of limit ordinals. The indices  are ordinal numbers defined as
are ordinal numbers defined as

if such an ordinal exists. Otherwise, we write  . Finally the Szlenk index is defined by
. Finally the Szlenk index is defined by  .
.
Remark 2.7.
It is known (see [18, Theorem 2] or [1, Theorem 5.2]) that  if and only if
if and only if  is an Asplund space. Since our results apply for Banach spaces satisfying
is an Asplund space. Since our results apply for Banach spaces satisfying  , from now on, we will only consider Asplund spaces.
, from now on, we will only consider Asplund spaces.
Theorem 2.8 (see [19]).
Let  be an Asplund space with
be an Asplund space with  . Then, there is an equivalent norm on
. Then, there is an equivalent norm on  such that the dual norm on
such that the dual norm on  is UKK*.
is UKK*.
Let  be a compact topological space. It is known (see, e.g., [1, Lemma 8.3]) that
be a compact topological space. It is known (see, e.g., [1, Lemma 8.3]) that  is an Asplund space if and only if
is an Asplund space if and only if  is scattered. For special scattered sets, we have a more precise result.
is scattered. For special scattered sets, we have a more precise result.
Theorem 2.9 (see [18, Theorem 24]).
Let  be a scattered compact space. The following assertions are equivalent:
be a scattered compact space. The following assertions are equivalent:
(i) ,
,
(ii) .
.
We will use the equivalent definition of the UKK* property given by the following lemma.
Lemma 2.10.
Assume that  is a Banach space. Then the dual norm is UKK* if and only if for every
is a Banach space. Then the dual norm is UKK* if and only if for every  , there exists
, there exists  such that if
such that if  is a net in the unit ball of
is a net in the unit ball of  convergent to
convergent to  in the weak* topology such that
in the weak* topology such that  , then
, then  .
.
Proof.
Assume that the above condition is satisfied and let  . Suppose that diam
. Suppose that diam  for every open neighborhood of
for every open neighborhood of  in the weak*-topology. We can choose
in the weak*-topology. We can choose  such that
such that  . Then,
. Then,  is a net in
is a net in  convergent to
convergent to  in the weak*-topology. Taking a subnet
in the weak*-topology. Taking a subnet  of
of  such that
such that  exists, we obtain
exists, we obtain  . Conversely, assume that the dual norm is UKK*. Let
. Conversely, assume that the dual norm is UKK*. Let  be a net in
be a net in  convergent to
convergent to  in the weak*-topology such that
in the weak*-topology such that  . Let
. Let  be an open neighborhood of
be an open neighborhood of  in the weak*-topology. There exist
in the weak*-topology. There exist  such that for every
such that for every  we have
we have  and
and  . Thus diam
. Thus diam  , which implies
, which implies  .
.
Remark 2.11.
Note that the above notion implies the sequential-UKK* condition, that is, the dual norm is (sequentially)-UKK* if for every  , there exists
, there exists  such that if
such that if  is a sequence in the unit ball of
is a sequence in the unit ball of  convergent to
convergent to  in the weak* topology such that
in the weak* topology such that  , then
, then  . Both conditions are equivalent if either
. Both conditions are equivalent if either  is separable (and, consequently, the weak*-topology restricted to bounded subsets of
is separable (and, consequently, the weak*-topology restricted to bounded subsets of  is metrizable) or
is metrizable) or  is reflexive (due to the angelicity of weak compact sets).
is reflexive (due to the angelicity of weak compact sets).
Theorem 2.12.
Let  be an Asplund space with
be an Asplund space with  . Then, there is an equivalent norm
. Then, there is an equivalent norm  on
on  such that
such that  and, hence,
and, hence,  satisfies the w-FPP.
satisfies the w-FPP.
Proof.
By Theorem 2.8, there exists an equivalent norm on  , such that the dual norm satisfies the UKK* property. We follow an argument inspired on that in the proof of Proposition III.11 in [15]. Assume that
, such that the dual norm satisfies the UKK* property. We follow an argument inspired on that in the proof of Proposition III.11 in [15]. Assume that  is a weakly null sequence in
is a weakly null sequence in  and
and  . For every
. For every  , choose
, choose  such that
such that  . Taking a subsequence, if necessary, we can assume that
. Taking a subsequence, if necessary, we can assume that  does exist. Let
does exist. Let  be a subnet of
be a subnet of  which is weak*-convergent to
which is weak*-convergent to  and such that
and such that  exists. Assume
exists. Assume  and choose an arbitrary
and choose an arbitrary  . Since
. Since  is a weakly null net, there exists
is a weakly null net, there exists  such that
such that  ,
,  and
and  for every
for every  . Thus, we have
. Thus, we have

which implies that  . If
. If  , from Lemma 2.10 we have that
, from Lemma 2.10 we have that  . Since
. Since

we have

Thus, 
Remark 2.13 s.
-
(1)
Following an argument as in the proof of Proposition III.11 in [15], we can also obtain the condition
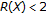 under the following more general assumption which is usually denoted as w-UKK* property: there exist
under the following more general assumption which is usually denoted as w-UKK* property: there exist 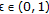 and
and  such that if
such that if 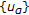 is a net in the unit ball of
is a net in the unit ball of 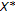 convergent to
convergent to  in the weak*-topology and such that
in the weak*-topology and such that 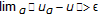 , then
, then 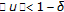 . However, this condition does not yield to an improvement of the above theorem, because if
. However, this condition does not yield to an improvement of the above theorem, because if  satisfies the w-UKK* property, there is a renorming of
satisfies the w-UKK* property, there is a renorming of  such that the dual norm satisfies the UKK* property. Indeed, it is easy to check that the w-UKK* property implies that the Szlenk index
such that the dual norm satisfies the UKK* property. Indeed, it is easy to check that the w-UKK* property implies that the Szlenk index  is finite for some
is finite for some  . Since the function
. Since the function 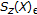 is submultiplicative [18, Proposition 4], we have that
is submultiplicative [18, Proposition 4], we have that  and thus
and thus 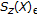 is finite for every positive
is finite for every positive  . Thus, the existence of an equivalent norm in
. Thus, the existence of an equivalent norm in  such that the dual norm satisfies the UKK* property is a consequence of Theorem 2.8.
such that the dual norm satisfies the UKK* property is a consequence of Theorem 2.8. -
(2)
We can also deduce some fixed point properties for the dual norm. First of all, we should mention that if
 is an Asplund space, then
is an Asplund space, then 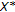 can be continuously embedded in
can be continuously embedded in  for some set
for some set  [22]. Thus, by the main result in [13],
[22]. Thus, by the main result in [13],  has an equivalent (in general non-dual) norm which satisfies the w-FPP. On the other hand, we know (see [23, Corollary 5.10]) that property UKK* implies that the coefficient
has an equivalent (in general non-dual) norm which satisfies the w-FPP. On the other hand, we know (see [23, Corollary 5.10]) that property UKK* implies that the coefficient 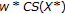 is greater than 1, where
is greater than 1, where 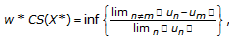 (2.7)
(2.7)
and the infimum is taken over all weak*-null sequences  in
in  such that both limits exist and
such that both limits exist and  . This condition implies that every separable weak*-compact subset of
. This condition implies that every separable weak*-compact subset of  has normal structure (see [24, Theorem 2] or [23, Proposition 5.3]). Thus,
has normal structure (see [24, Theorem 2] or [23, Proposition 5.3]). Thus,  admits a dual equivalent norm such that if
admits a dual equivalent norm such that if  is a nonexpansive mapping defined from a separable weak*-compact convex subset
is a nonexpansive mapping defined from a separable weak*-compact convex subset  of
of  into
into  , then
, then  has a fixed point (see [24, Theorem 1]). If
has a fixed point (see [24, Theorem 1]). If  is reflexive, the separability assumption can be removed, because the condition
is reflexive, the separability assumption can be removed, because the condition  implies normal structure for weakly compact subsets of
implies normal structure for weakly compact subsets of  and we recover the first mentioned renorming result (now, for a dual norm because any equivalent norm is a dual norm in a reflexive space [25]). However, in this case we obtain a stronger result because we have an equivalent norm in
and we recover the first mentioned renorming result (now, for a dual norm because any equivalent norm is a dual norm in a reflexive space [25]). However, in this case we obtain a stronger result because we have an equivalent norm in  such that
such that  endowed with the new norm satisfies the w-FPP and
endowed with the new norm satisfies the w-FPP and  endowed with the dual norm satisfies the w-FPP either (Theorem 3.4 in the last section will show a different way to prove a stronger result). Also in the reflexive case, since
endowed with the dual norm satisfies the w-FPP either (Theorem 3.4 in the last section will show a different way to prove a stronger result). Also in the reflexive case, since  is nearly uniform convex, we can also assure that
is nearly uniform convex, we can also assure that  satisfies the w-FPP for nonexpansive multivalued mappings (with compact convex values) (see, e.g., [26]).
satisfies the w-FPP for nonexpansive multivalued mappings (with compact convex values) (see, e.g., [26]).
Theorem 2.12 jointly with [16, Theorem 2.5] yields to the main result in this paper.
Theorem 2.14.
Let  be a Banach space with
be a Banach space with  . Assume that
. Assume that  is another Banach space, such that there exists a continuous one-to-one mapping
is another Banach space, such that there exists a continuous one-to-one mapping  . Then,
. Then,  can be renormed to satisfy the w-FPP.
can be renormed to satisfy the w-FPP.
Assume that  is an uncountable set. We can consider that
is an uncountable set. We can consider that  is endowed with the discrete topology. Let
is endowed with the discrete topology. Let  be the one-point compactification of
be the one-point compactification of  . Then,
. Then,  is isomorphic to
is isomorphic to  by defining
by defining  by
by  . Thus any space which can be continuously embedded in
. Thus any space which can be continuously embedded in  , can be also embedded in
, can be also embedded in  , where
, where  . From Theorems 2.9 and 2.14, we obtain the following result which strictly improves the main result in [13], because as mentioned in the introduction and proved in [21], there exists a compact set (Ciesielski-Pol's compact), such that
. From Theorems 2.9 and 2.14, we obtain the following result which strictly improves the main result in [13], because as mentioned in the introduction and proved in [21], there exists a compact set (Ciesielski-Pol's compact), such that  , but
, but  cannot be continuously embedded in
cannot be continuously embedded in  for any set
for any set  . The same result is proved in [16] using a direct but very technical argument.
. The same result is proved in [16] using a direct but very technical argument.
Corollary 2.15.
Let  be a Banach space which can be continuously embedded in
be a Banach space which can be continuously embedded in  for some compact set
for some compact set  such that
such that  . Then,
. Then,  can be renormed to satisfy the w-FPP.
can be renormed to satisfy the w-FPP.
3. Genericity of the w-FPP and Szlenk Index
Following the approach in [27], for a Banach space  , with closed unit ball
, with closed unit ball  , we denote by
, we denote by  the Baire space of all equivalent norms with the metric
the Baire space of all equivalent norms with the metric  .
.
In a Baire space, we can regard first category sets as negligible sets. However, we can also consider a deeper notion of negligible set. We should remember that a set  in a topological space
in a topological space  is nowhere dense if its closure has empty interior. If
is nowhere dense if its closure has empty interior. If  is a metric space, this fact means that for every
is a metric space, this fact means that for every  and
and  , there exists
, there exists  and
and  such that
such that  . A more strict condition is the following.
. A more strict condition is the following.
Definition 3.1.
Let  be a metric space. A subset
be a metric space. A subset  of
of  is said to be porous if there exist
is said to be porous if there exist  and
and  such that for every
such that for every  and
and  , there exists
, there exists  such that
such that  . A subset
. A subset  of
of  is called
is called  -
- if
if  is the union of a countable family of porous sets.
is the union of a countable family of porous sets.
Porous and  -porous set can be considered "small" in
-porous set can be considered "small" in  . In particular a
. In particular a  -porous set is obviously of Baire first category and, for
-porous set is obviously of Baire first category and, for  , a
, a  -porous set is a null set with respect to the Lebesgue measure.
-porous set is a null set with respect to the Lebesgue measure.
In [28, Theorem 14], it is proved that if  is a Banach space such that
is a Banach space such that  , then there exists a
, then there exists a  -porous set
-porous set  such that if
such that if  the space
the space  satisfies the w-FPP. From this and Theorem 2.12, we easily obtain the following generic result.
satisfies the w-FPP. From this and Theorem 2.12, we easily obtain the following generic result.
Corollary 3.2.
Assume that  is a Banach space with
is a Banach space with  and
and  is the set of all norms in
is the set of all norms in  which are equivalent to the original norm with the metric
which are equivalent to the original norm with the metric  . Then, there exists a
. Then, there exists a  -porous set
-porous set  such that if
such that if  the space
the space  satisfies the w-FPP.
satisfies the w-FPP.
In particular, we obtain the following generic result, which can be regarded as an improvement of the result in [20] about the w-FPP in  .
.
Corollary 3.3.
Assume that  and
and  is the set of all norms in
is the set of all norms in  which are equivalent to the supremum norm with the metric
which are equivalent to the supremum norm with the metric  . Then, there exists a
. Then, there exists a  -porous set
-porous set  such that if
such that if  , the space
, the space  satisfies the w-FPP.
satisfies the w-FPP.
For general reflexive spaces (independently of the Szlenk index), we can use the main result in [29] to prove a strong generic result in the sense of the Remarks 2.13. If  is a norm in a Banach space
is a norm in a Banach space  , we will denote by
, we will denote by  the dual norm on the dual space
the dual norm on the dual space  and by
and by  the Baire space of all equivalent norms to
the Baire space of all equivalent norms to  with the metric
with the metric  .
.
Theorem 3.4.
Let  be a reflexive space. There exists a residual subset
be a reflexive space. There exists a residual subset  of
of  (i.e.,
(i.e.,  is of Baire fist category) such that for every
is of Baire fist category) such that for every  , the spaces
, the spaces  and (
and ( satisfy both the w-FPP.
satisfy both the w-FPP.
Proof.
By [29, Corollary 2.5], there exist a residual subset  of
of  and another residual subset
and another residual subset  in
in  such that if
such that if  and
and  , the spaces
, the spaces  and
and  satisfy the w-FPP. We claim that the mapping
satisfy the w-FPP. We claim that the mapping  defined by
defined by  is an homeomorphism from
is an homeomorphism from  onto
onto  . Indeed, this mapping is clearly one-one. Moreover,
. Indeed, this mapping is clearly one-one. Moreover,  is onto because any equivalent norm in a reflexive space is a dual norm [25]. It is enough to prove that
is onto because any equivalent norm in a reflexive space is a dual norm [25]. It is enough to prove that  is continuous because
is continuous because  is similar to
is similar to  . Fixed
. Fixed  and
and  . Denote by
. Denote by  the positive number
the positive number  . Assume that
. Assume that  . Note that
. Note that  for every
for every  . Furthermore,
. Furthermore,  implies
implies

and, analogously,  implies
implies

Assume that  and
and  . We have
. We have

Thus  . Analogously,
. Analogously,  which implies
which implies  for every
for every  in the unit ball of
in the unit ball of  , that is,
, that is,  . Finally, defining
. Finally, defining  , we conclude the proof.
, we conclude the proof.
Remark 3.5.
We do not know if a porous version of the above theorem does hold. In fact, we do not know either if Corollary 2.5 in [29] holds in the sense of porosity. Furthermore, the mapping  defined in the proof of Theorem 3.4 is a homeomorphism, but it is not uniformly continuous. Indeed, the sequence of norms in
defined in the proof of Theorem 3.4 is a homeomorphism, but it is not uniformly continuous. Indeed, the sequence of norms in  , defined by
, defined by  , is a Cauchy sequence, but the dual sequence
, is a Cauchy sequence, but the dual sequence  is not. Thus, the
is not. Thus, the  -porosity of
-porosity of  does not, in general, imply the
does not, in general, imply the  -porosity of
-porosity of  .
.
References
Deville R, Godefroy G, Zizler V: Smoothness and Renormings in Banach Spaces, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 64. Longman Scientific & Technical, Harlow, UK; 1993:xii+376.
Godefroy G: Renormings of Banach spaces. In Handbook of the Geometry of Banach Spaces. Volume 1. North-Holland, Amsterdam, The Netherlands; 2001:781–835.
Fabian M, Habala P, Hájek P, Montesinos Santalucía V, Pelant J, Zizler V: Functional Analysis and Infinite-dimensional Geometry, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC. Volume 8. Springer, New York, NY, USA; 2001:x+451.
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Takahashi W: Nonlinear Functional Analysis, Fixed Point Theory and Its Application. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Ayerbe Toledano JM, Domínguez Benavides T, López Acedo G: Measures of Noncompactness in Metric Fixed Point Theory, Operator Theory: Advances and Applications. Volume 99. Birkhäuser, Basel, Switzerland; 1997:viii+211.
Partington JR: Equivalent norms on spaces of bounded functions. Israel Journal of Mathematics 1980,35(3):205–209. 10.1007/BF02761190
Partington JR: Subspaces of certain Banach sequence spaces. The Bulletin of the London Mathematical Society 1981,13(2):163–166.
Alspach DE: A fixed point free nonexpansive map. Proceedings of the American Mathematical Society 1981,82(3):423–424. 10.1090/S0002-9939-1981-0612733-0
Day MM, James RC, Swaminathan S: Normed linear spaces that are uniformly convex in every direction. Canadian Journal of Mathematics 1971,23(6):1051–1059.
Kutzarova DN, Troyanski SL: Reflexive Banach spaces without equivalent norms which are uniformly convex or uniformly differentiable in every direction. Studia Mathematica 1982,72(1):91–95.
Kirk WA: Some questions in metric fixed point theory. In Recent Advances on Metric Fixed Point Theory (Seville, 1995), Ciencias. Volume 48. Universidad de Sevilla, Seville, Spain; 1996:73–97.
Domínguez Benavides T: A renorming of some nonseparable Banach spaces with the fixed point property. Journal of Mathematical Analysis and Applications 2009,350(2):525–530. 10.1016/j.jmaa.2008.02.049
García-Falset J: Stability and fixed points for nonexpansive mappings. Houston Journal of Mathematics 1994,20(3):495–506.
García Falset J: The fixed point property in Banach spaces with the NUS-property. Journal of Mathematical Analysis and Applications 1997,215(2):532–542. 10.1006/jmaa.1997.5657
Domínguez Benavides T, Phothi S: The fixed point property under renorming in some classes of Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2010,72(3–4):1409–1416. 10.1016/j.na.2009.08.024
Szlenk W: The non-existence of a separable reflexive Banach space universal for all separable reflexive Banach spaces. Studia Mathematica 1968, 30: 53–61.
Lancien G: A survey on the Szlenk index and some of its applications. RACSAM. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas 2006,100(1–2):209–235.
Raja M: On weak∗ uniformly Kadec-Klee renormings.
Domínguez Benavides T, Japón Pineda MA: Fixed points of nonexpansive mappings in spaces of continuous functions. Proceedings of the American Mathematical Society 2005,133(10):3037–3046. 10.1090/S0002-9939-05-08149-9
Godefroy G, Pelant J, Whitfield JHM, Zizler V: Banach space properties of Ciesielski-Pol's
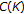 space. Proceedings of the American Mathematical Society 1988,103(4):1087–1093.
space. Proceedings of the American Mathematical Society 1988,103(4):1087–1093.Fabian M, Godefroy G: The dual of every Asplund space admits a projectional resolution of the identity. Mathematische Annalen 1982, 258: 349–351. 10.1007/BF01450688
Prus S: Geometrical background of metric fixed point theory. In Handbook of Metric Fixed Point Theory. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:93–132.
Domínguez Benavides T, García Falset J, Japón Pineda MA: The -fixed point property for nonexpansive mappings. Abstract and Applied Analysis 1998,3(3–4):343–362. 10.1155/S1085337598000591
Williams JP: A "metric" characterization of reflexivity. Proceedings of the American Mathematical Society 1967, 18: 163–165.
Domínguez Benavides T, Gavira B: The fixed point property for multivalued nonexpansive mappings. Journal of Mathematical Analysis and Applications 2007,328(2):1471–1483. 10.1016/j.jmaa.2006.06.059
Fabian M, Zajiček L, Zizler V: On residuality of the set of rotunds norms on a Banach space. Studia Mathematica 1988,91(2):141–151.
Domínguez Benavides T, Phothi S: Porosity of the Fixed Point Property under Renorming, Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2008.
Domínguez Benavides T, Phothi S: Genericity of the fixed point property for reflexive spaces under renormings. to appear in Contemporary Mathematics
Acknowledgments
The author is very grateful to M. Fabian for some valuable comments. The author is partially supported by DGES, Grant BFM2006-13997-C02-01 and Junta de Andalucía, Grant FQM-127. This work is dedicated to W. Takahashi acknowledging his wide and deep legacy in Fixed Point Theory.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Benavides, T. The Szlenk Index and the Fixed Point Property under Renorming. Fixed Point Theory Appl 2010, 268270 (2010). https://doi.org/10.1155/2010/268270
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/268270
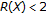 under the following more general assumption which is usually denoted as w-UKK* property: there exist
under the following more general assumption which is usually denoted as w-UKK* property: there exist 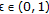 and
and  such that if
such that if 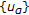 is a net in the unit ball of
is a net in the unit ball of 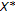 convergent to
convergent to  in the weak*-topology and such that
in the weak*-topology and such that 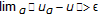 , then
, then 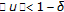 . However, this condition does not yield to an improvement of the above theorem, because if
. However, this condition does not yield to an improvement of the above theorem, because if  satisfies the w-UKK* property, there is a renorming of
satisfies the w-UKK* property, there is a renorming of  such that the dual norm satisfies the UKK* property. Indeed, it is easy to check that the w-UKK* property implies that the Szlenk index
such that the dual norm satisfies the UKK* property. Indeed, it is easy to check that the w-UKK* property implies that the Szlenk index  is finite for some
is finite for some  . Since the function
. Since the function 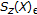 is submultiplicative [
is submultiplicative [ and thus
and thus 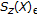 is finite for every positive
is finite for every positive  . Thus, the existence of an equivalent norm in
. Thus, the existence of an equivalent norm in  such that the dual norm satisfies the UKK* property is a consequence of Theorem 2.8.
such that the dual norm satisfies the UKK* property is a consequence of Theorem 2.8. is an Asplund space, then
is an Asplund space, then 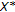 can be continuously embedded in
can be continuously embedded in  for some set
for some set  [
[ has an equivalent (in general non-dual) norm which satisfies the w-FPP. On the other hand, we know (see [
has an equivalent (in general non-dual) norm which satisfies the w-FPP. On the other hand, we know (see [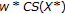 is greater than 1, where
is greater than 1, where 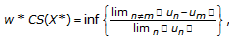
 space. Proceedings of the American Mathematical Society 1988,103(4):1087–1093.
space. Proceedings of the American Mathematical Society 1988,103(4):1087–1093.