- Research Article
- Open access
- Published:
Strong and Weak Convergence of the Modified Proximal Point Algorithms in Hilbert Space
Fixed Point Theory and Applications volume 2010, Article number: 240450 (2010)
Abstract
For a monotone operator  , we shall show weak convergence of Rockafellar's proximal point algorithm to some zero of
, we shall show weak convergence of Rockafellar's proximal point algorithm to some zero of  and strong convergence of the perturbed version of Rockafellar's to
and strong convergence of the perturbed version of Rockafellar's to  under some relaxed conditions, where
under some relaxed conditions, where  is the metric projection from
is the metric projection from  onto
onto  . Moreover, our proof techniques are simpler than some existed results.
. Moreover, our proof techniques are simpler than some existed results.
1. Introduction
Throughout this paper, let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  , and let
, and let  be on identity operator in
be on identity operator in  . We shall denote by
. We shall denote by  the set of all positive integers, by
the set of all positive integers, by  the set of all zeros of
the set of all zeros of  , that is,
, that is,  and by
and by  the set of all fixed points of
the set of all fixed points of  , that is,
, that is,  . When
. When  is a sequence in
is a sequence in  , then
, then  (resp.,
(resp.,  ,
,  ) will denote strong (resp., weak, weak
) will denote strong (resp., weak, weak ) convergence of the sequence
) convergence of the sequence  to
to  .
.
Let  be an operator with domain
be an operator with domain  and range
and range  in
in  . Recall that
. Recall that  is said to be monotone if
is said to be monotone if

A monotone operator  is said to be maximal monotone if
is said to be maximal monotone if  is monotone and
is monotone and  for all
for all  .
.
In fact, theory of monotone operator is very important in nonlinear analysis and is connected with theory of differential equations. It is well known (see [1]) that many physically significant problems can be modeled by the initial-value problems of the form

where  is a monotone operator in an appropriate space. Typical examples where such evolution equations occur can be found in the heat and wave equations or Schrodinger equations. On the other hand, a variety of problems, including convex programming and variational inequalities, can be formulated as finding a zero of monotone operators. Then the problem of finding a solution
is a monotone operator in an appropriate space. Typical examples where such evolution equations occur can be found in the heat and wave equations or Schrodinger equations. On the other hand, a variety of problems, including convex programming and variational inequalities, can be formulated as finding a zero of monotone operators. Then the problem of finding a solution  with
with  has been investigated by many researchers; see, for example, Bruck [2], Rockafellar [3], Brézis and Lions [4], Reich [5, 6], Nevanlinna and Reich [7], Bruck and Reich [8], Jung and Takahashi [9], Khang [10], Minty [11], Xu [12], and others. Some of them dealt with the weak convergence of (1.4) and others proved strong convergence theorems by imposing strong assumptions on
has been investigated by many researchers; see, for example, Bruck [2], Rockafellar [3], Brézis and Lions [4], Reich [5, 6], Nevanlinna and Reich [7], Bruck and Reich [8], Jung and Takahashi [9], Khang [10], Minty [11], Xu [12], and others. Some of them dealt with the weak convergence of (1.4) and others proved strong convergence theorems by imposing strong assumptions on  .
.
One popular method of solving  is the proximal point algorithm of Rockafellar [3] which is recognized as a powerful and successful algorithm in finding a zero of monotone operators. Starting from any initial guess
is the proximal point algorithm of Rockafellar [3] which is recognized as a powerful and successful algorithm in finding a zero of monotone operators. Starting from any initial guess  , this proximal point algorithm generates a sequence
, this proximal point algorithm generates a sequence  given by
given by

where  for all
for all  is the resolvent of
is the resolvent of  on the space
on the space  . Rockafellar's [3] proved the weak convergence of his algorithm (1.3) provided that the regularization sequence
. Rockafellar's [3] proved the weak convergence of his algorithm (1.3) provided that the regularization sequence  remains bounded away from zero and the error sequence
remains bounded away from zero and the error sequence  satisfies the condition
satisfies the condition  . G
. G ler's example [13] however shows that in an infinite-dimensional Hilbert space, Rochafellar's algorithm (1.3) has only weak convergence. Recently several authors proposed modifications of Rochafellar's proximal point algorithm (1.3) to have strong convergence. For examples, Solodov and Svaiter [14] and Kamimura and Takahashi [15] studied a modified proximal point algorithm by an additional projection at each step of iteration. Lehdili and Moudafi [16] obtained the convergence of the sequence
ler's example [13] however shows that in an infinite-dimensional Hilbert space, Rochafellar's algorithm (1.3) has only weak convergence. Recently several authors proposed modifications of Rochafellar's proximal point algorithm (1.3) to have strong convergence. For examples, Solodov and Svaiter [14] and Kamimura and Takahashi [15] studied a modified proximal point algorithm by an additional projection at each step of iteration. Lehdili and Moudafi [16] obtained the convergence of the sequence  generated by the algorithm
generated by the algorithm

where  is viewed as a Tikhonov regularization of
is viewed as a Tikhonov regularization of  . Using the technique of variational distance, Lehdili and Moudafi [16] were able to prove convergence theorems for the algorithm (1.4) and its perturbed version, under certain conditions imposed upon the sequences
. Using the technique of variational distance, Lehdili and Moudafi [16] were able to prove convergence theorems for the algorithm (1.4) and its perturbed version, under certain conditions imposed upon the sequences  and
and  . For a maximal monotone operator
. For a maximal monotone operator  , Xu [12] and Song and Yang [17] used the technique of nonexpansive mappings to get convergence theorems for
, Xu [12] and Song and Yang [17] used the technique of nonexpansive mappings to get convergence theorems for  defined by the perturbed version of the algorithm (1.4):
defined by the perturbed version of the algorithm (1.4):

In this paper, under more relaxed conditions on the sequences  and
and  , we shall show that the sequence
, we shall show that the sequence  generated by (1.5) converges strongly to
generated by (1.5) converges strongly to  (where
(where  is the metric projection from
is the metric projection from  onto
onto  ) and the sequence
) and the sequence  generated by (1.3) weakly converges to some
generated by (1.3) weakly converges to some  . Moreover, our proof techniques are simpler than those of Lehdili and Moudafi [16], Xu [12], and Song and Yang [17].
. Moreover, our proof techniques are simpler than those of Lehdili and Moudafi [16], Xu [12], and Song and Yang [17].
2. Preliminaries and Basic Results
Let  be a monotone operator with
be a monotone operator with  . We use
. We use  and
and  to denote the resolvent and Yosida's approximation of
to denote the resolvent and Yosida's approximation of  , respectively. Namely,
, respectively. Namely,

For  and
and  , the following is well known. For more details, see [18, Pages 369–400] or [3, 19].
, the following is well known. For more details, see [18, Pages 369–400] or [3, 19].
(i) for all
for all  ;
;
(ii) for all
for all  ;
;
(iii) is a single-valued nonexpansive mapping for each
is a single-valued nonexpansive mapping for each  (i.e.,
(i.e.,  for all
for all  );
);
(iv) is closed and convex;
is closed and convex;
-
(v)
(The Resolvent Identity) For
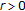 and
and 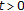 and
and 
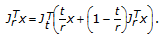 (2.2)
(2.2)
In the rest of this paper, it is always assumed that  is nonempty so that the metric projection
is nonempty so that the metric projection  from
from  onto
onto  is well defined. It is known that
is well defined. It is known that  is nonexpansive and characterized by the inequality: given
is nonexpansive and characterized by the inequality: given  and
and  ; then
; then  if and only if
if and only if

In order to facilitate our investigation in the next section we list a useful lemma.
Lemma 2.1 (see Xu [20, Lemma  ]).
]).
Let  be a sequence of nonnegative real numbers satisfying the property:
be a sequence of nonnegative real numbers satisfying the property:

where  ,
,  , and
, and  satisfy the conditions (i)
satisfy the conditions (i)  (ii) either
(ii) either  or
or  (iii)
(iii)  for all
for all  and
and  Then
Then  converges to zero as
converges to zero as  .
.
3. Strongly Convergence Theorems
Let  be a monotone operator on a Hilbert space
be a monotone operator on a Hilbert space  . Then
. Then  is a single-valued nonexpansive mapping from
is a single-valued nonexpansive mapping from  to
to  . When
. When  is a nonempty closed convex subset of
is a nonempty closed convex subset of  such that
such that  for all
for all  (here
(here  is closure of
is closure of  ), then we have
), then we have  for
for  and all
and all  , and hence the following iteration is well defined
, and hence the following iteration is well defined

Next we will show strong convergence of  defined by (3.1) to find a zero of
defined by (3.1) to find a zero of  . For reaching this objective, we always assume
. For reaching this objective, we always assume  in the sequel.
in the sequel.
Theorem 3.1.
Let  be a monotone operator on a Hilbert space
be a monotone operator on a Hilbert space  with
with  . Assume that
. Assume that  is a nonempty closed convex subset of
is a nonempty closed convex subset of  such that
such that  for all
for all  and for an anchor point
and for an anchor point  and an initial value
and an initial value  ,
,  is iteratively defined by (3.1). If
is iteratively defined by (3.1). If  and
and  satisfy
satisfy
(i)
(ii)
(iii)
then the sequence  converges strongly to
converges strongly to  , where
, where  is the metric projection from
is the metric projection from  onto
onto  .
.
Proof.
The proof consists of the following steps:
Step 1.
The sequence  is bounded. Let
is bounded. Let  , then
, then  and for some
and for some  , we have
, we have

So, the sequences  ,
,  , and
, and  are bounded.
are bounded.
Step 2.
 for each
for each  . Since
. Since

we have

Step 3.
 Indeed, we can take a subsequence
Indeed, we can take a subsequence  of
of  such that
such that

We may assume that  by the reflexivity of
by the reflexivity of  and the boundedness of
and the boundedness of  . Then
. Then  . In fact, since
. In fact, since

then, for some constant  , we have
, we have

Thus,

Take  on two sides of the above equation by means of (3.4), we must have
on two sides of the above equation by means of (3.4), we must have  . So,
. So,  . Hence, noting the projection inequality (2.3), we obtain
. Hence, noting the projection inequality (2.3), we obtain

Step 4.
 . Indeed,
. Indeed,

Therefore,

where  So, an application of Lemma 2.1 onto (3.11) yields the desired result.
So, an application of Lemma 2.1 onto (3.11) yields the desired result.
Theorem 3.2.
Let  be as Theorem 3.1, the condition (iii)
be as Theorem 3.1, the condition (iii)  is replaced by the following condition:
is replaced by the following condition:

Then the sequence  converges strongly to
converges strongly to  , where
, where  is the metric projection from
is the metric projection from  onto
onto  .
.
Proof.
From the proof of Theorem 3.1, we can observe that Steps 1, 3 and 4 still hold. So we only need show to Step 2:  for each
for each  .
.
We first estimate  From the resolvent identity (2.2), we have
From the resolvent identity (2.2), we have

Therefore, for a constant  with
with  ,
,

It follows from Lemma 2.1 that

As  then
then

Since  , then there exists
, then there exists  and a positive integer
and a positive integer  such that for all
such that for all  ,
,  . Thus for each
. Thus for each  , we also have
, we also have

we have 
Corollary 3.3.
Let  be as Theorem 3.1 or 3.2. Suppose that
be as Theorem 3.1 or 3.2. Suppose that  is a maximal monotone operator on
is a maximal monotone operator on  and for
and for  ,
,  is defined by (3.1). Then the sequence
is defined by (3.1). Then the sequence  converges strongly to
converges strongly to  , where
, where  is the metric projection from
is the metric projection from  onto
onto  .
.
Proof.
Since  is a maximal monotone, then
is a maximal monotone, then  is monotone and satisfies the condition
is monotone and satisfies the condition  for all
for all  . Putting
. Putting  , the desired result is reached.
, the desired result is reached.
Corollary 3.4.
Let  be as Theorem 3.1 or 3.2. Suppose that
be as Theorem 3.1 or 3.2. Suppose that  is a monotone operator on
is a monotone operator on  satisfying the condition
satisfying the condition  for all
for all  and for
and for  ,
,  is defined by (3.1). If
is defined by (3.1). If  is convex, then the sequence
is convex, then the sequence  converges strongly to
converges strongly to  , where
, where  is the metric projection from
is the metric projection from  onto
onto  .
.
Proof.
Taking  , following Theorem 3.1 or 3.2, we easily obtain the desired result.
, following Theorem 3.1 or 3.2, we easily obtain the desired result.
4. Weakly Convergence Theorems
For a monotone operator  , if
, if  for all
for all  and
and  , then the iteration
, then the iteration  (
( ) is well defined. Next we will show weak convergence of
) is well defined. Next we will show weak convergence of  under some assumptions.
under some assumptions.
Theorem 4.1.
Let  be a monotone operator on a Hilbert space
be a monotone operator on a Hilbert space  with
with  . Assume that
. Assume that  for all
for all  and for an initial value
and for an initial value  , iteratively define
, iteratively define

If  satisfies
satisfies

then the sequence  converges weakly to some
converges weakly to some  .
.
Proof.
Take  , we have
, we have

Therefore,  is nonincreasing and bounded below, and hence the limit
is nonincreasing and bounded below, and hence the limit  exists for each
exists for each  . Further,
. Further,  is bounded. So we have
is bounded. So we have

Hence,

As  is weakly sequentially compact by the reflexivity of
is weakly sequentially compact by the reflexivity of  , and hence we may assume that there exists a subsequence
, and hence we may assume that there exists a subsequence  of
of  such that
such that  . Using the proof technique of Step 3 in Theorem 3.1, we must have that
. Using the proof technique of Step 3 in Theorem 3.1, we must have that  .
.
Now we prove that  converges weakly to
converges weakly to  . Supposed that there exists another subsequence
. Supposed that there exists another subsequence  of
of  which weakly converges to some
which weakly converges to some  . We also have
. We also have  . Because
. Because  exists for each
exists for each  and
and

thus,

Similarly, we also have

Adding up the above two equations, we must have  . So,
. So,  .
.
In a summary, we have proved that the set  is weakly sequentially compact and each cluster point in the weak topology equals to
is weakly sequentially compact and each cluster point in the weak topology equals to  . Hence,
. Hence,  converges weakly to
converges weakly to  . The proof is complete.
. The proof is complete.
Theorem 4.2.
Let  be a maximal monotone operator on a Hilbert space
be a maximal monotone operator on a Hilbert space  with
with  . For an initial value
. For an initial value  , iteratively define
, iteratively define

If  and
and  satisfy
satisfy

then the sequence  converges weakly to some
converges weakly to some  .
.
Proof.
Take  and
and  , we have
, we have

It follows from Liu [21, Lemma  ] that the limit
] that the limit  exists for each
exists for each  and hence both
and hence both  and
and  are bounded. So we have
are bounded. So we have

Hence,

The remainder of the proof is the same as Theorem 4.1; we omit it.
References
Zeidler E: Nonlinear Functional Analysis and Its Applications, Part II: Monotone Operators. Springer, Berlin, Germany; 1985.
Bruck RE Jr.: A strongly convergent iterative solution of
 for a maximal monotone operator in Hilbert space. Journal of Mathematical Analysis and Applications 1974, 48: 114–126. 10.1016/0022-247X(74)90219-4
for a maximal monotone operator in Hilbert space. Journal of Mathematical Analysis and Applications 1974, 48: 114–126. 10.1016/0022-247X(74)90219-4Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization 1976,14(5):877–898. 10.1137/0314056
Brézis H, Lions P-L: Produits infinis de résolvantes. Israel Journal of Mathematics 1978,29(4):329–345. 10.1007/BF02761171
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1979,67(2):274–276. 10.1016/0022-247X(79)90024-6
Reich S: Strong convergence theorems for resolvents of accretive operators in Banach spaces. Journal of Mathematical Analysis and Applications 1980,75(1):287–292. 10.1016/0022-247X(80)90323-6
Nevanlinna O, Reich S: Strong convergence of contraction semigroups and of iterative methods for accretive operators in Banach spaces. Israel Journal of Mathematics 1979,32(1):44–58. 10.1007/BF02761184
Bruck RE, Reich S: A general convergence principle in nonlinear functional analysis. Nonlinear Analysis: Theory, Methods & Applications 1980,4(5):939–950. 10.1016/0362-546X(80)90006-1
Jung JS, Takahashi W: Dual convergence theorems for the infinite products of resolvents in Banach spaces. Kodai Mathematical Journal 1991,14(3):358–365. 10.2996/kmj/1138039461
Khang DB: On a class of accretive operators. Analysis 1990,10(1):1–16.
Minty GJ: On the monotonicity of the gradient of a convex function. Pacific Journal of Mathematics 1964, 14: 243–247.
Xu H-K: A regularization method for the proximal point algorithm. Journal of Global Optimization 2006,36(1):115–125. 10.1007/s10898-006-9002-7
Güler O: On the convergence of the proximal point algorithm for convex minimization. SIAM Journal on Control and Optimization 1991,29(2):403–419. 10.1137/0329022
Solodov MV, Svaiter BF: Forcing strong convergence of proximal point iterations in a Hilbert space. Mathematical Programming. Series A 2000,87(1):189–202.
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM Journal on Optimization 2002,13(3):938–945. 10.1137/S105262340139611X
Lehdili N, Moudafi A: Combining the proximal algorithm and Tikhonov regularization. Optimization 1996,37(3):239–252. 10.1080/02331939608844217
Song Y, Yang C: A note on a paper "A regularization method for the proximal point algorithm". Journal of Global Optimization 2009,43(1):171–174. 10.1007/s10898-008-9279-9
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics (New York). John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Takahashi W: Nonlinear Functional Analysis—Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Xu H-K: Strong convergence of an iterative method for nonexpansive and accretive operators. Journal of Mathematical Analysis and Applications 2006,314(2):631–643. 10.1016/j.jmaa.2005.04.082
Liu Q: Iterative sequences for asymptotically quasi-nonexpansive mappings with error member. Journal of Mathematical Analysis and Applications 2001,259(1):18–24. 10.1006/jmaa.2000.7353
Acknowledgments
The authors are grateful to the anonymous referee for his/her valuable suggestions which helps to improve this manuscript. This work is supported by Youth Science Foundation of Henan Normal University(2008qk02) and by Natural Science Research Projects (Basic Research Project) of Education Department of Henan Province (2009B110011, 2009B110001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chai, X., Li, B. & Song, Y. Strong and Weak Convergence of the Modified Proximal Point Algorithms in Hilbert Space. Fixed Point Theory Appl 2010, 240450 (2010). https://doi.org/10.1155/2010/240450
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/240450
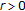 and
and 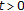 and
and 
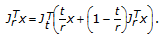
 for a maximal monotone operator in Hilbert space. Journal of Mathematical Analysis and Applications 1974, 48: 114–126. 10.1016/0022-247X(74)90219-4
for a maximal monotone operator in Hilbert space. Journal of Mathematical Analysis and Applications 1974, 48: 114–126. 10.1016/0022-247X(74)90219-4