- Research Article
- Open access
- Published:
Generalizations of the Nash Equilibrium Theorem in the KKM Theory
Fixed Point Theory and Applications volume 2010, Article number: 234706 (2010)
Abstract
The partial KKM principle for an abstract convex space is an abstract form of the classical KKM theorem. In this paper, we derive generalized forms of the Ky Fan minimax inequality, the von Neumann-Sion minimax theorem, the von Neumann-Fan intersection theorem, the Fan-type analytic alternative, and the Nash equilibrium theorem for abstract convex spaces satisfying the partial KKM principle. These results are compared with previously known cases for  -convex spaces. Consequently, our results unify and generalize most of previously known particular cases of the same nature. Finally, we add some detailed historical remarks on related topics.
-convex spaces. Consequently, our results unify and generalize most of previously known particular cases of the same nature. Finally, we add some detailed historical remarks on related topics.
1. Introduction
In 1928, John von Neumann found his celebrated minimax theorem [1] and, in 1937, his intersection lemma [2], which was intended to establish easily his minimax theorem and his theorem on optimal balanced growth paths. In 1941, Kakutani [3] obtained a fixed point theorem for multimaps, from which von Neumann's minimax theorem and intersection lemma were easily deduced.
In 1950, John Nash [4, 5] established his celebrated equilibrium theorem by applying the Brouwer or the Kakutani fixed point theorem. In 1952, Fan [6] and Glicksberg [7] extended Kakutani's theorem to locally convex Hausdorff topological vector spaces, and Fan generalized the von Neumann intersection lemma by applying his own fixed point theorem. In 1972, Himmelberg [8] obtained two generalizations of Fan's fixed point theorem [6] and applied them to generalize the von Neumann minimax theorem by following Kakutani's method in [3].
In 1961, Ky Fan [9] obtained his KKM lemma and, in 1964 [10], applied it to another intersection theorem for a finite family of sets having convex sections. This was applied in 1966 [11] to a proof of the Nash equilibrium theorem. This is the origin of the application of the KKM theory to the Nash theorem. In 1969, Ma [12] extended Fan's intersection theorem [10] to infinite families and applied it to an analytic formulation of Fan type and to the Nash theorem for arbitrary families.
Note that all of the above results are mainly concerned with convex subsets of topological vector spaces; see Granas [13]. Later, many authors tried to generalize them to various types of abstract convex spaces. The present author also extended them in our previous works [14–28] in various directions. In fact, the author had developed theory of generalized convex spaces (simply,  -convex spaces) related to the KKM theory and analytical fixed point theory. In the framework of
-convex spaces) related to the KKM theory and analytical fixed point theory. In the framework of  -convex spaces, we obtained some minimax theorems and the Nash equilibrium theorems in our previous works [17, 18, 21, 22], based on coincidence theorems or intersection theorems for finite families of sets, and in [22], based on continuous selection theorems for the Fan-Browder maps.
-convex spaces, we obtained some minimax theorems and the Nash equilibrium theorems in our previous works [17, 18, 21, 22], based on coincidence theorems or intersection theorems for finite families of sets, and in [22], based on continuous selection theorems for the Fan-Browder maps.
In our recent works [24–26], we studied the foundations of the KKM theory on abstract convex spaces. The partial KKM principle for an abstract convex space is an abstract form of the classical KKM theorem. A KKM space is an abstract convex space satisfying the partial KKM principle and its "open" version. We noticed that many important results in the KKM theory are closely related to KKM spaces or spaces satisfying the partial KKM principle. Moreover, a number of such results are equivalent to each other.
On the other hand, some other authors studied particular types of KKM spaces and deduced some Nash-type equilibrium theorem from the corresponding partial KKM principle, for example, [17, 21, 29–33], explicitly, and many more in the literature, implicitly. Therefore, in order to avoid unnecessary repetitions for each particular type of KKM spaces, it would be necessary to state clearly them for spaces satisfying the partial KKM principle. This was simply done in [27].
In this paper, we study several stages of such developments from the KKM principle to the Nash theorem and related results within the frame of the KKM theory of abstract convex spaces. In fact, we clearly show that a sequence of statements from the partial KKM principle to the Nash equilibria can be obtained for any space satisfying the partial KKM principle. This unifies previously known several proper examples of such sequences for particular types of KKM spaces. More precisely, our aim in this paper is to obtain generalized forms of the KKM space versions of known results due to von Neumann, Sion, Nash, Fan, Ma, and many followers. These results are mainly obtained by  fixed point method,
fixed point method,  continuous selection method, or
continuous selection method, or  the KKM method. In this paper, we follow method
the KKM method. In this paper, we follow method  and will compare our results to corresponding ones already obtained by method
and will compare our results to corresponding ones already obtained by method 
In Section 2, we state basic facts and examples of abstract convex spaces in our previous works [24–26]. Section 3 deals with a characterization of the partial KKM principle and shows that such principle is equivalent to the generalized Fan-Browder fixed point theorem. In Section 4, we deduce a general Fan-type minimax inequality from the partial KKM principle. Section 5 deals with various von Neumann-Sion-type minimax theorems for abstract convex spaces.
In Section 6, a collective fixed point theorem is deduced as a generalization of the Fan-Browder fixed point theorem. Section 7 deals with the Fan-type intersection theorems for sets with convex sections in product abstract convex spaces satisfying the partial KKM principle. In Section 8, we deduce a Fan-type analytic alternative and its consequences. Section 9 is devoted to various generalizations of the Nash equilibrium theorem and their consequences. Finally, in Section 10, some known results related to the Nash theorem and historical remarks are added.
This paper is a revised and extended version of [22, 27] and a supplement to [24–26], where some other topics on abstract convex spaces can be found.
2. Abstract Convex Spaces and the KKM Spaces
Multimaps are also called simply maps. Let  denote the set of all nonempty finite subsets of a set
denote the set of all nonempty finite subsets of a set  . Recall the following in [24–26].
. Recall the following in [24–26].
Definition 2.1.
An abstract convex space consists of a topological space
consists of a topological space  , a nonempty set
, a nonempty set  , and a multimap
, and a multimap  with nonempty values
with nonempty values  for
for  .
.
For any  , the
, the  -convex hull of
-convex hull of  is denoted and defined by
is denoted and defined by

A subset  of
of  is called a
is called a  -convex subset of
-convex subset of  relative to
relative to  if for any
if for any  we have that
we have that  , that is,
, that is,  .
.
When  , the space is denoted by
, the space is denoted by  . In such case, a subset
. In such case, a subset  of
of  is said to be
is said to be  -convex if
-convex if  ; in other words,
; in other words,  is
is  -convex relative to
-convex relative to  . In case
. In case  , let
, let  .
.
Example 2.2.
The following are known examples of abstract convex spaces.
-
(1)
A triple
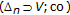 is given for the original KKM theorem [34], where
is given for the original KKM theorem [34], where 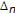 is the standard
is the standard  -simplex,
-simplex,  is the set of its vertices
is the set of its vertices  , and co:
, and co:  is the convex hull operation.
is the convex hull operation. -
(2)
A triple
 is given, where
is given, where 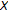 and
and 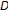 are subsets of a t.v.s.
are subsets of a t.v.s. 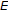 such that co
such that co  and
and  co. Fan's celebrated KKM lemma [9] is for
co. Fan's celebrated KKM lemma [9] is for 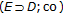 .
. -
(3)
A convex space
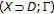 is a triple where
is a triple where 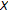 is a subset of a vector space such that co
is a subset of a vector space such that co 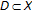 , and each
, and each  is the convex hull of
is the convex hull of 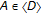 equipped with the Euclidean topology. This concept generalizes the one due to Lassonde for
equipped with the Euclidean topology. This concept generalizes the one due to Lassonde for 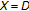 ; see [35]. However he obtained several KKM-type theorems w.r.t.
; see [35]. However he obtained several KKM-type theorems w.r.t. 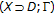 .
. -
(4)
A triple
 is called an
is called an 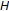 -space if
-space if  is a topological space and
is a topological space and 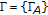 is a family of contractible (or, more generally,
is a family of contractible (or, more generally,  -connected) subsets of
-connected) subsets of 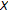 indexed by
indexed by  such that
such that 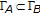 whenever
whenever  . If
. If  , then
, then  is called a
is called a  -space by Horvath [36, 37].
-space by Horvath [36, 37]. -
(5)
Hyperconvex metric spaces due to Aronszajn and Panitchpakdi are particular cases of
 -spaces; see [37].
-spaces; see [37]. -
(6)
Hyperbolic spaces due to Reich and Shafrir [38] are also particular cases of
 -spaces. This class of metric spaces contains all normed vector spaces, all Hadamard manifolds, the Hilbert ball with the hyperbolic metric, and others. Note that an arbitrary product of hyperbolic spaces is also hyperbolic.
-spaces. This class of metric spaces contains all normed vector spaces, all Hadamard manifolds, the Hilbert ball with the hyperbolic metric, and others. Note that an arbitrary product of hyperbolic spaces is also hyperbolic. -
(7)
Any topological semilattice
 with path-connected interval is introduced by Horvath and Llinares [39].
with path-connected interval is introduced by Horvath and Llinares [39]. -
(8)
A generalized convex space or a
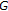 -convex space
-convex space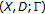 due to Park is an abstract convex space such that for each
due to Park is an abstract convex space such that for each 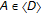 with the cardinality
with the cardinality 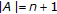 there exists a continuous function
there exists a continuous function 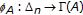 such that
such that 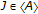 implies that
implies that  .
.
Here,  is the face of
is the face of  corresponding to
corresponding to  , that is, if
, that is, if 
 and
and  , then
, then  .
.
For details, see references of [17, 21, 22, 40–42].
-
(9)
A
 -space
-space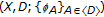 consists of a topological space
consists of a topological space 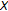 , a nonempty set
, a nonempty set 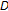 , and a family of continuous functions
, and a family of continuous functions  (that is, singular
(that is, singular  -simplexes) for
-simplexes) for 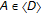 with
with 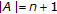 . Every
. Every  -space can be made into a
-space can be made into a  -convex space; see [43]. Recently
-convex space; see [43]. Recently  -spaces are called
-spaces are called  -spaces in [44] and
-spaces in [44] and 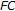 -spaces [43] or simplicial spaces [45] when
-spaces [43] or simplicial spaces [45] when  .
. -
(10)
Suppose that
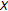 is a closed convex subset of a complete
is a closed convex subset of a complete  -tree
-tree 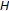 , and for each
, and for each  ,
, 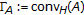 , where
, where 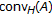 is the intersection of all closed convex subsets of
is the intersection of all closed convex subsets of 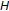 that contain
that contain  ; see Kirk and Panyanak [46]. Then
; see Kirk and Panyanak [46]. Then 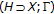 is an abstract convex space.
is an abstract convex space. -
(11)
A topological space
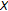 with a convexity in the sense of Horvath [47] is another example.
with a convexity in the sense of Horvath [47] is another example. -
(12)
A
 -space due to Briec and Horvath [30] is an abstract convex space.
-space due to Briec and Horvath [30] is an abstract convex space.
Note that each of (2)–(12) has a large number of concrete examples and that all examples (1)–(9) are  -convex spaces.
-convex spaces.
Definition 2.3.
Let  be an abstract convex space. If a multimap
be an abstract convex space. If a multimap  satisfies
satisfies

then  is called a KKM map.
is called a KKM map.
Definition 2.4.
Thepartial KKM principle for an abstract convex space  is the statement that, for any closed-valued KKM map
is the statement that, for any closed-valued KKM map  , the family
, the family  has the finite intersection property. The KKM principle is the statement that the same property also holds for any open-valued KKM map.
has the finite intersection property. The KKM principle is the statement that the same property also holds for any open-valued KKM map.
An abstract convex space is called a KKM space if it satisfies the KKM principle.
In our recent works [24–26], we studied the foundations of the KKM theory on abstract convex spaces and noticed that many important results therein are related to the partial KKM principle.
Example 2.5.
We give examples of KKM spaces as follows.
-
(1)
Every
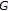 -convex space is a KKM space [18].
-convex space is a KKM space [18]. -
(2)
A connected linearly ordered space
 can be made into a KKM space [26].
can be made into a KKM space [26]. -
(3)
The extended long line
 is a KKM space
is a KKM space 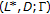 with the ordinal space
with the ordinal space  ; see [26]. But
; see [26]. But  is not a
is not a 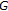 -convex space.
-convex space. -
(4)
For a closed convex subset
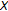 of a complete
of a complete  -tree
-tree 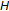 , and
, and 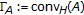 for each
for each 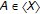 , the triple
, the triple  satisfies the partial KKM principle; see [46]. Later we found that
satisfies the partial KKM principle; see [46]. Later we found that 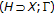 is a KKM space [48].
is a KKM space [48]. -
(5)
Horvath's convex space
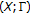 with the weak Van de Vel property is a KKM space, where
with the weak Van de Vel property is a KKM space, where 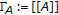 for each
for each 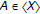 ; see [47, 48].
; see [47, 48]. -
(6)
A
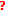 -space due to Briec and Horvath [30] is a KKM space.
-space due to Briec and Horvath [30] is a KKM space.
Now we have the following diagram for triples  :
:

It is not known yet whether there is a space satisfying the partial KKM principle that is not a KKM space.
3. The KKM Principle and the Fan-Browder Map
Let  be an abstract convex space.
be an abstract convex space.
Recall the following equivalent form of [26, Theorem 8.2].
Theorem 3.1.
Suppose that  satisfies the partial KKM principle and a map
satisfies the partial KKM principle and a map  satisfies the following.
satisfies the following.
 is closed valued.
is closed valued.
 is a KKM map (i.e.,
is a KKM map (i.e.,  for all
for all  ).
).
There exists a nonempty compact subset  of
of  such that one of the following holds:
such that one of the following holds:
(i) ,
,
(ii) for some
for some  ,
,
(iii)for each  , there exists a compact
, there exists a compact  -convex subset
-convex subset  of
of  relative to some
relative to some  such that
such that  and
and

Then 
Remark 3.2.
Conditions (i)–(iii) in  are called compactness conditions or coercivity conditions. In this paper, we mainly adopt simply (i), that is,
are called compactness conditions or coercivity conditions. In this paper, we mainly adopt simply (i), that is,  is compact. However, most of results can be reformulated to the ones adopting (ii) or (iii).
is compact. However, most of results can be reformulated to the ones adopting (ii) or (iii).
Definition 3.3.
For a topological space  and an abstract convex space
and an abstract convex space  , a multimap
, a multimap  is called a
is called a  -map or a Fan-Browder map provided that there exists a multimap
-map or a Fan-Browder map provided that there exists a multimap  satisfying the follwing:
satisfying the follwing:
(a)for each  (i.e.,
(i.e.,  implies that
implies that  ),
),
(b) Int
Int  for some
for some  .
.
Here, Int denotes the interior with respect to  and, for each
and, for each  ,
,  .
.
There are several equivalent formulations of the partial KKM principle; see [26]. For example, it is equivalent to the Fan-Browder-type fixed point theorem as follows.
Theorem 3.4 (see [26]).
An abstract convex space  satisfies the partial KKM principle if and only if any
satisfies the partial KKM principle if and only if any  -map
-map  has a fixed point
has a fixed point  , that is,
, that is,  .
.
The following is known.
Lemma 3.5.
Let  be any family of abstract convex spaces. Let
be any family of abstract convex spaces. Let  be equipped with the product topology and
be equipped with the product topology and  . For each
. For each  , let
, let  be the projection. For each
be the projection. For each  , define
, define  . Then
. Then  is an abstract convex space.
is an abstract convex space.
Let  be a family of
be a family of  -convex spaces. Then
-convex spaces. Then  is a
is a  -convex space.
-convex space.
It is not known yet whether this holds for KKM spaces.
From now on, for simplicity, we are mainly concerned with compact abstract convex spaces  satisfying the partial KKM principle. For example, any compact
satisfying the partial KKM principle. For example, any compact  -convex space, any compact
-convex space, any compact  -space, or any compact convex space is such a space.
-space, or any compact convex space is such a space.
4. The Fan-Type Minimax Inequalities
Recall that an extended real-valued function  , where
, where  is a topological space, is lower [resp., upper] semicontinuous (l.s.c.) (resp., u.s.c.) if
is a topological space, is lower [resp., upper] semicontinuous (l.s.c.) (resp., u.s.c.) if  (resp.,
(resp.,  ) is open for each
) is open for each  .
.
For an abstract convex space  , an extended real-valued function
, an extended real-valued function  is said to be quasiconcave (resp., quasiconvex) if
is said to be quasiconcave (resp., quasiconvex) if  (resp.,
(resp.,  ) is
) is  -convex for each
-convex for each  .
.
From the partial KKM principle we can deduce a very general version of the Ky Fan minimax inequality as follows.
Theorem 4.1.
Let  be an abstract convex space satisfying the partial KKM principle,
be an abstract convex space satisfying the partial KKM principle,  extended real functions, and
extended real functions, and  such that
such that
(3.1)for each  ,
,  is closed,
is closed,
(3.2)for each  ,
,  ,
,
(3.3)the compactness condition (1.3) holds for  .
.
Then either (i) there exists a  such that
such that  for all
for all  or (ii) there exists an
or (ii) there exists an  such that
such that 
Proof.
Let  be a map defined by
be a map defined by  for
for  . Then each
. Then each  is closed by (3.1).
is closed by (3.1).
Ca (i):
(i):  is a KKM map.
is a KKM map.
By Theorem 3.1, we have  . Hence, there exists a
. Hence, there exists a  such that
such that  for all
for all  , that is,
, that is,  for all
for all  .
.
Ca (ii):
(ii):  is not a KKM map.
is not a KKM map.
Then there exists  such that
such that  . Hence there exists an
. Hence there exists an  such that
such that  for each
for each  , or equivalently
, or equivalently  for each
for each  . Since
. Since  contains
contains  , by
, by  we have
we have  and hence,
and hence,  .
.
Corollary 4.2.
Under the hypothesis of Theorem 4.1, let  Then
Then

Example 4.3.
 For a compact convex subset
For a compact convex subset  of a t.v.s. and
of a t.v.s. and  , if
, if  is quasiconcave, then (3.2) holds; and if
is quasiconcave, then (3.2) holds; and if  is l.s.c., then (3.1) holds. Therefore, Corollary 4.2 generalizes the Ky Fan minimax inequality [49].
is l.s.c., then (3.1) holds. Therefore, Corollary 4.2 generalizes the Ky Fan minimax inequality [49].
 For a convex space
For a convex space  and
and  , Corollary 4.2 reduces to Cho et al. [50, Theorem 9].
, Corollary 4.2 reduces to Cho et al. [50, Theorem 9].
 There is a very large number of generalizations of the Fan minimax inequality for convex spaces,
There is a very large number of generalizations of the Fan minimax inequality for convex spaces,  -spaces,
-spaces,  -convex spaces, and others. These would be particular forms of Corollary 4.2. For example, see Park [18, Theorem 11], where
-convex spaces, and others. These would be particular forms of Corollary 4.2. For example, see Park [18, Theorem 11], where  is a
is a  -convex space.
-convex space.
 Some particular versions of Corollary 4.2 were given in [27].
Some particular versions of Corollary 4.2 were given in [27].
5. The von Neumann-Sion-Type Minimax Theorems
Let  and
and  be abstract convex spaces. For their product, as in the Lemma 3.5 we can define
be abstract convex spaces. For their product, as in the Lemma 3.5 we can define  for
for  .
.
Theorem 5.1.
Let  be the product abstract convex space, and let
be the product abstract convex space, and let  be four functions, then
be four functions, then

Suppose that
 for each
for each  ,
,
for each  and
and  ,
,  is
is  -convex; for each
-convex; for each  and
and  ,
,  is
is  -convex,
-convex,
for each  , there exists a finite set
, there exists a finite set  such that
such that

for each  , there exists a finite set
, there exists a finite set  such that
such that

If  satisfies the partial KKM principle, then
satisfies the partial KKM principle, then

Proof.
Suppose that there exists a real  such that
such that

For the abstract convex space

define two maps  by
by


for  and
and  , respectively. Then each
, respectively. Then each  is nonempty and
is nonempty and  -convex and
-convex and  is covered by a finite number of open sets
is covered by a finite number of open sets  's. Moreover,
's. Moreover,

This implies that  for all
for all  . Then
. Then  is a
is a  -map. Therefore, by Theorem 3.4, we have
-map. Therefore, by Theorem 3.4, we have  such that
such that  . Therefore,
. Therefore,  , a contradiction.
, a contradiction.
Example 5.2.
For convex spaces  ,
,  and
and  , Theorem 5.1 reduces to that by Cho et al. [50, Theorem 8].
, Theorem 5.1 reduces to that by Cho et al. [50, Theorem 8].
Corollary 5.3.
Let  and
and  be compact abstract convex spaces, let
be compact abstract convex spaces, let  be the product abstract convex space, and let
be the product abstract convex space, and let  be functions satisfying the following:
be functions satisfying the following:
(1) for each
for each  ,
,
(2)for each  is l.s.c. and
is l.s.c. and  is quasiconvex on
is quasiconvex on 
(3)for each  is quasiconcave and
is quasiconcave and  is u.s.c. on
is u.s.c. on  .
.
If  satisfies the partial KKM principle, then
satisfies the partial KKM principle, then

Proof.
Note that  is l.s.c. on
is l.s.c. on  and
and  is u.s.c. on
is u.s.c. on  . Therefore, both sides of the inequality exist. Then all the requirements of Theorem 5.1 are satisfied.
. Therefore, both sides of the inequality exist. Then all the requirements of Theorem 5.1 are satisfied.
Example 5.4.
-
(1)
Particular or slightly different versions of Corollary 5.3 are obtained by Liu [51], Granas [13, Théorèmes 3.1 et 3.2], and Shih and Tan [52, Theorem 4] for convex subsets of t.v.s.
-
(2)
For
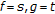 , Corollary 5.3 reduces to [27, Theorem 3].
, Corollary 5.3 reduces to [27, Theorem 3].
For the case  , Corollary 5.3 reduces to the following.
, Corollary 5.3 reduces to the following.
Corollary 5.5 (see [27]).
Let  and
and  be compact abstract convex spaces and let
be compact abstract convex spaces and let  be an extended real function such that
be an extended real function such that
(1)for each  is l.s.c. and quasiconvex on
is l.s.c. and quasiconvex on  ,
,
(2)for each  is u.s.c. and quasiconcave on
is u.s.c. and quasiconcave on  .
.
If  satisfies the partial KKM principle, then
satisfies the partial KKM principle, then
(i) has a saddle point
has a saddle point  ,
,
(ii)one has

Example 5.6.
We list historically well-known particular forms of Corollary 5.5 in chronological order as follows.
(1)von Neumann [1], Kakutani [3].  and
and  are compact convex subsets of Euclidean spaces and
are compact convex subsets of Euclidean spaces and  is continuous.
is continuous.
(2)Nikaidô [53]. Euclidean spaces above are replaced by Hausdorff topological vector spaces, and  is continuous in each variable.
is continuous in each variable.
(3)Sion [54].  and
and  are compact convex subsets of topological vector spaces in Corollary 5.5.
are compact convex subsets of topological vector spaces in Corollary 5.5.
(4)Komiya [55, Theorem 3].  and
and  are compact convex spaces in the sense of Komiya.
are compact convex spaces in the sense of Komiya.
(5)Horvath [36, Proposition 5.2].  and
and  are
are  -spaces with
-spaces with  being compact and without assuming the compactness of
being compact and without assuming the compactness of  .
.
In these two examples, Hausdorffness of  is assumed since they used the partition of unity argument.
is assumed since they used the partition of unity argument.
(6)Bielawski [29, Theorem (4.13)].  and
and  are compact spaces having certain simplicial convexities.
are compact spaces having certain simplicial convexities.
(7)Park [17, Theorem 5].  and
and  are
are  -convex spaces.
-convex spaces.
In 1999, we deduced the following von Neumann–Sion type minimax theorem for  -convex spaces based on a continuous selection theorem:
-convex spaces based on a continuous selection theorem:
Theorem 5.7 (see [17]).
Let  and
and  be
be  -convex spaces,
-convex spaces,  Hausdorff compact,
Hausdorff compact,  an extended real function, and
an extended real function, and  . Suppose that
. Suppose that
(5.1) is l.s.c. on
is l.s.c. on  and
and  is
is  -convex for each
-convex for each  and
and  ,
,
(5.2) is u.s.c. on
is u.s.c. on  and
and  is
is  -convex for each
-convex for each  and
and  . Then
. Then

Example 5.8.
6. Collective Fixed Point Theorems
We have the following collective fixed point theorem.
Theorem 6.1.
Let  be a finite family of compact abstract convex spaces such that
be a finite family of compact abstract convex spaces such that  satisfies the partial KKM principle, and for each
satisfies the partial KKM principle, and for each  is a
is a  -map. Then there exists a point
-map. Then there exists a point  such that
such that  that is,
that is,  for each
for each  .
.
Proof.
Let  be the companion map corresponding to the
be the companion map corresponding to the  -map
-map  . Define
. Define  by
by

We show that  is a
is a  -map with the companion map
-map with the companion map  . In fact, we have
. In fact, we have

where  . Since each
. Since each  is open, we have
is open, we have
(a)for each  ,
,  is open.
is open.
Note that

and hence,

Therefore, we have
(b)for each  implies that
implies that  .
.
Moreover, let  . Since
. Since  is the companion map corresponding to the
is the companion map corresponding to the  -map
-map  , for each
, for each  , there exists
, there exists  such that
such that

where  Since
Since  is compact, we have
is compact, we have
(c) for some
for some  .
.
Since  satisfies the partial KKM principle, by Theorem 3.4, the
satisfies the partial KKM principle, by Theorem 3.4, the  -map
-map  has a fixed point.
has a fixed point.
Example 6.2.
-
(1)
If
 ,
, 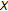 is a convex space, and
is a convex space, and  , then Theorem 6.1 reduces to the well-known Fan-Browder fixed point theorem; see Park [56].
, then Theorem 6.1 reduces to the well-known Fan-Browder fixed point theorem; see Park [56]. -
(2)
For the case
 , Theorem 6.1 for a convex space
, Theorem 6.1 for a convex space 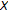 was obtained by Ben-El-Mechaiekh et al. [69, Theorem 1] and Simons [57, Theorem 4.3]. This was extended by many authors; see Park [56].
was obtained by Ben-El-Mechaiekh et al. [69, Theorem 1] and Simons [57, Theorem 4.3]. This was extended by many authors; see Park [56].
We have already the following collective fixed point theorem for arbitrary family of  -convex spaces.
-convex spaces.
Theorem 6.3 (see [40]).
Let  be a family of compact Hausdorff
be a family of compact Hausdorff  -convex spaces,
-convex spaces,  , and for each
, and for each  let
let  be a
be a  -map. Then there exists a point
-map. Then there exists a point  such that
such that  that is,
that is,  for each
for each  .
.
Example 6.4.
In case when  are all
are all  -spaces, Theorem 6.3 reduces to Tarafdar [58, Theorem 2.3]. This is applied to sets with
-spaces, Theorem 6.3 reduces to Tarafdar [58, Theorem 2.3]. This is applied to sets with  -convex sections [58, Theorem 3.1] and to existence of equilibrium point of an abstract economy [58, Theorem 4.1 and Corollary 4.1]. These results also can be extended to
-convex sections [58, Theorem 3.1] and to existence of equilibrium point of an abstract economy [58, Theorem 4.1 and Corollary 4.1]. These results also can be extended to  -convex spaces and we will not repeat then here.
-convex spaces and we will not repeat then here.
Remark 6.5.
Each of Theorems 6.1, 7.1, 8.1, 9.1, and 9.4, respectively, in this paper is based on the KKM method and concerns with finite families of abstract convex spaces such that their product satisfies the partial KKM principle. Each of them has a corresponding Theorems 6.3, 7.3, 8.3, 9.2 and 9.6, respectively, based on continuous selection method for infinite families of Hausdorff  -convex spaces. Note that for finite families the Hausdorffness is redundant in these corresponding theorems.
-convex spaces. Note that for finite families the Hausdorffness is redundant in these corresponding theorems.
7. Intersection Theorems for Sets with Convex Sections
In our previous work [17], from a  -convex space version of the Fan-Browder fixed point theorem, we deduced a Fan-type intersection theorem for
-convex space version of the Fan-Browder fixed point theorem, we deduced a Fan-type intersection theorem for  subsets of a cartesian product of
subsets of a cartesian product of  compact
compact  -convex spaces. This was applied to obtain a von Neumann-sion-type minimax theorem and a Nash-type equilibrium theorem for
-convex spaces. This was applied to obtain a von Neumann-sion-type minimax theorem and a Nash-type equilibrium theorem for  -convex spaces.
-convex spaces.
In the present section, we generalize the abovementioned intersection theorem to product abstract convex spaces satisfying the partial KKM principle.
The collective fixed point theorem in Section 6 can be reformulated to a generalization of various Fan-type intersection theorems for sets with convex sections as follows.
Let  be a family of sets, and let
be a family of sets, and let  be fixed. Let
be fixed. Let

If  and
and  , then let
, then let  denote the
denote the  th coordinate of
th coordinate of  . If
. If  and
and  , then let
, then let  be defined as follows: its
be defined as follows: its  th coordinate is
th coordinate is  and for
and for  the
the  th coordinate is
th coordinate is  . Therefore, any
. Therefore, any  can be expressed as
can be expressed as  for any
for any  , where
, where  denotes the projection of
denotes the projection of  in
in  .
.
Theorem 7.1.
Let  be a finite family of compact abstract convex spaces such that
be a finite family of compact abstract convex spaces such that  satisfies the partial KKM principle and, for each
satisfies the partial KKM principle and, for each  , let
, let  and
and  be subsets of
be subsets of  satisfying the following.
satisfying the following.
 For each
For each  .
.
 For each
For each  is open in
is open in  .
.
Then  .
.
Proof.
We apply Theorem 6.1 with multimaps  given by
given by  and
and  for each
for each  . Then for each
. Then for each  we have the following.
we have the following.
(a)For each  , we have
, we have  .
.
(b)For each  , we have
, we have

Hence,

Note that  is open in
is open in  and that
and that  is a
is a  -map. Therefore, by Theorem 6.1, there exists
-map. Therefore, by Theorem 6.1, there exists  such that
such that  for all
for all  . Hence
. Hence  .
.
Example 7.2.
For convex spaces  , particular forms of Theorem 7.1 have appeared as follows:
, particular forms of Theorem 7.1 have appeared as follows:
Fan [10, Théeorème 1].  for all
for all  .
.
Fan [11, Theorem  ].
].  and
and  for
for  .
.
From these results, Fan [11] deduced an analytic formulation, fixed point theorems, extension theorems of monotone sets, and extension theorems for invariant vector subspaces.
For particular types of  -convex spaces, Theorem 7.1 was known as follows.
-convex spaces, Theorem 7.1 was known as follows.
Bielawski [29, Proposition  and Theorem
and Theorem  ].
].  have the finitely local convexity.
have the finitely local convexity.
Kirk et al. [32, Theorem 5.2].  are hyperconvex metric spaces.
are hyperconvex metric spaces.
Park [17, Theorem 4], [18, Theorem 19]. In [17], from a  -convex space version of the Fan-Browder fixed point theorem, we deduced a Fan-type intersection theorem for
-convex space version of the Fan-Browder fixed point theorem, we deduced a Fan-type intersection theorem for  subsets of a cartesian product of
subsets of a cartesian product of  compact
compact  -convex spaces. This was applied to obtain a von Neumann-Sion-type minimax theorem and a Nash-type equilibrium theorem for
-convex spaces. This was applied to obtain a von Neumann-Sion-type minimax theorem and a Nash-type equilibrium theorem for  -convex spaces.
-convex spaces.
Park [27, Theorem 4]. We gave a different proof.
In [22], a collective fixed point theorem was reformulated to a generalization of various Fan-type intersection theorems for arbitrary number of sets with convex sections as follows.
Theorem 7.3 (see [22]).
Let  be a family of Hausdorff compact
be a family of Hausdorff compact  -convex spaces and, for each
-convex spaces and, for each  , let
, let  and
and  be subsets of
be subsets of  satisfying the following.
satisfying the following.
 For each
For each 
 For each
For each  is open in
is open in  .
.
Then  .
.
Example 7.4.
For convex subsets  of topological vector spaces, particular forms of Theorem 7.3 have appeared as follows.
of topological vector spaces, particular forms of Theorem 7.3 have appeared as follows.
Ma [12, Theorem 2]. The case  for all
for all  with a different proof is given.
with a different proof is given.
Chang [59, Theorem 4.2] obtained Theorem 7.3 with a different proof. The author also obtained a noncompact version of Theorem 7.3 as in [59, Theorem 4.3].
Park [19, Theorem 4.2].  are convex spaces.
are convex spaces.
Note that if  is finite in Theorem 7.3, the Hausdorffness is redundant by Theorem 7.1.
is finite in Theorem 7.3, the Hausdorffness is redundant by Theorem 7.1.
8. The Fan-Type Analytic Alternatives
From the intersection Theorem 7.1, we can deduce the following equivalent form of a generalized Fan-type minimax inequality or analytic alternative. Our method is based on that of Fan [9, 10] and Ma [12].
Theorem 8.1.
Let  be a finite family of compact abstract convex spaces such that
be a finite family of compact abstract convex spaces such that  satisfies the partial KKM principle and, for each
satisfies the partial KKM principle and, for each  , let
, let  be real functions satisfying
be real functions satisfying
 for each
for each 
for each  is quasiconcave on
is quasiconcave on 
for each  is l.s.c. on
is l.s.c. on  .
.
Let  be a family of real numbers. Then either
be a family of real numbers. Then either
(a)there exist an  and an
and an  such that
such that

or (b)there exists an  such that
such that

Proof.
Suppose that (a) does not hold, that is, for any  and any
and any  , there exists an
, there exists an  such that
such that  . Let
. Let

for each  . Then
. Then
(1)for each 
(2)for each  ,
,  is
is  -convex,
-convex,
(3)for each  ,
,  is open in
is open in  .
.
Therefore, by Theorem 7.1, there exists an  . This is equivalent to (b).
. This is equivalent to (b).
Example 8.2.
Fan [9, Théorème 2], [10, Theorem 3].  are convex subsets of t.v.s., and
are convex subsets of t.v.s., and  for all
for all  . From this, fan [9, 10] deduced Sion's minimax theorem [54], the Tychonoff fixed point theorem, solutions to systems of convex inequalities, extremum problems for matrices, and a theorem of Hardy-Littlewood-Pólya.
. From this, fan [9, 10] deduced Sion's minimax theorem [54], the Tychonoff fixed point theorem, solutions to systems of convex inequalities, extremum problems for matrices, and a theorem of Hardy-Littlewood-Pólya.
From the intersection Theorem 7.3, we can deduce the following equivalent form of a generalized Fan-type minimax inequality or analytic alternative.
Theorem 8.3 (see [22]).
Let  be a family of compact Hausdorff
be a family of compact Hausdorff  -convex spaces and, for each
-convex spaces and, for each  , let
, let  be real functions as in Theorem 8.1. Then the conclusion of Theorem 8.1 holds.
be real functions as in Theorem 8.1. Then the conclusion of Theorem 8.1 holds.
Example 8.4.
-
(1)
Ma [12, Theorem 3].
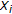 are convex subsets of t.v.s. and
are convex subsets of t.v.s. and  for all
for all 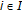 .
. -
(2)
Park [19, Theorem 8.1].
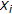 are convex spaces.
are convex spaces.
Remark 8.5.
-
(1)
We obtained Theorem 8.1 from Theorem 7.1. As was pointed out by Fan [9] for his case, we can deduce Theorem 7.1 from Theorem 8.1 by considering the characteristic functions of the sets
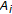 and
and  .
. -
(2)
The conclusion of Theorems 8.1 and 8.3 can be stated as follows

then (b) holds; see Fan [9, 10].
-
(3)
For
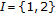 , Theorems 8.1 and 8.3 imply the Fan minimax inequality.
, Theorems 8.1 and 8.3 imply the Fan minimax inequality.
9. The Nash-Type Equilibrium Theorems
From Theorem 8.1, we obtain the following form of the Nash-Fan-type equilibrium theorems in [27] with different proofs.
Theorem 9.1.
Let  be a finite family of compact abstract convex spaces such that
be a finite family of compact abstract convex spaces such that  satisfies the partial KKM principle and, for each
satisfies the partial KKM principle and, for each  , let
, let  be real functions such that
be real functions such that
(9.0) for each
for each 
(9.1) for each  ,
,  is quasiconcave on
is quasiconcave on 
(9.2) for each  ,
,  is u.s.c. on
is u.s.c. on 
(9.3) for each  ,
,  is l.s.c. on
is l.s.c. on  .
.
Then there exists a point  such that
such that

Proof.
Since each  is compact, by
is compact, by  for any
for any  ,
,  exists for all
exists for all  and all
and all  . Hence Theorem 8.1(a) does not hold. Then by Theorem 8.1(b), there exists an
. Hence Theorem 8.1(a) does not hold. Then by Theorem 8.1(b), there exists an  such that
such that  for all
for all  . Since
. Since  is arbitrary, the conclusion follows.
is arbitrary, the conclusion follows.
This is not comparable to the following generalized Nash-Ma type theorem:
Theorem 9.2 (see [22]).
Let  be a family of compact Hausdorff
be a family of compact Hausdorff  -convex spaces and, for each
-convex spaces and, for each  , let
, let  be real functions satisfying (9.0)–(9.3). Then there exists a point
be real functions satisfying (9.0)–(9.3). Then there exists a point  such that
such that

Example 9.3.
Park [19, Theorem 8.2].  are convex spaces.
are convex spaces.
From Theorem 9.1 for  , we obtain the following form of the Nash-Fan-type equilibrium theorem for abstract convex spaces.
, we obtain the following form of the Nash-Fan-type equilibrium theorem for abstract convex spaces.
Theorem 9.4.
Let  be a finite family of compact abstract convex spaces such that
be a finite family of compact abstract convex spaces such that  satisfies the partial KKM principle and, for each
satisfies the partial KKM principle and, for each  , let
, let  be a function such that
be a function such that
(10.1) for each  ,
,  is quasiconcave on
is quasiconcave on 
(10.2) for each  ,
,  is u.s.c. on
is u.s.c. on 
(10.3) for each  ,
,  is l.s.c. on
is l.s.c. on  .
.
Then there exists a point  such that
such that

Example 9.5.
For continuous functions  , a number of particular forms of Theorem 9.4 have appeared for convex subsets
, a number of particular forms of Theorem 9.4 have appeared for convex subsets  of Hausdorff topological vector spaces as follows:
of Hausdorff topological vector spaces as follows:
(1)Nash [5, Theorem 1] where  are subsets of Euclidean spaces,
are subsets of Euclidean spaces,
(2)Nikaido and Isoda [60, Theorem 3.2],
(3)Fan [10, Theorem 4],
(4)Tan et al. [61, Theorem 2.1].
For particular types of  -convex spaces
-convex spaces  and continuous functions
and continuous functions  , particular forms of Theorem 9.4 have appeared as follows.
, particular forms of Theorem 9.4 have appeared as follows.
(5)Bielawski [29, Theorem 4.16].  have the finitely local convexity.
have the finitely local convexity.
(6)Kirk et al. [32, Theorem  ].
].  are hyperconvex metric spaces.
are hyperconvex metric spaces.
(7)Park [17, Theorem 6.1], [18, Theorem  ].
].  are
are  -convex spaces.
-convex spaces.
(8)Park [21, Theorem 4.7]. A variant of Theorem 9.4 is under the hypothesis that  is a compact
is a compact  -convex space and
-convex space and  are continuous functions.
are continuous functions.
(9)González et al. [31]. Each  is a compact, sequentially compact
is a compact, sequentially compact  -space and each
-space and each  is continuous as in 8.
is continuous as in 8.
(10)Briec and Horvath [30, Theorem  ]. Each
]. Each  is a compact
is a compact  -convex set and each
-convex set and each  is continuous as in 8.
is continuous as in 8.
From Theorem 9.2, we obtain the following generalization of the Nash-Ma-type equilibrium theorem for  -convex spaces.
-convex spaces.
Theorem 9.6 (see [22]).
Let  be a family of compact Hausdorff
be a family of compact Hausdorff  -convex spaces and, for each
-convex spaces and, for each  , let
, let  be a function satisfying conditions (
be a function satisfying conditions ( )–(
)–( ). Then there exists a point
). Then there exists a point  such that
such that

Example 9.7.
For continuous functions  and for convex subsets
and for convex subsets  of Hausdorff topological vector spaces, Theorem 9.6 was due to Ma [12, Theorem 4].
of Hausdorff topological vector spaces, Theorem 9.6 was due to Ma [12, Theorem 4].
The point  in the conclusion of Theorems 9.4 or 9.6 is called a Nash equilibrium. This concept is a natural extension of the local maxima and the saddle point as follows.
in the conclusion of Theorems 9.4 or 9.6 is called a Nash equilibrium. This concept is a natural extension of the local maxima and the saddle point as follows.
In case  is a singleton, we obtain the following.
is a singleton, we obtain the following.
Corollary 9.8.
Let  be a closed bounded convex subset of a reflexive Banach space
be a closed bounded convex subset of a reflexive Banach space  and
and  a quasiconcave u.s.c. function. Then
a quasiconcave u.s.c. function. Then  attains its maximum on
attains its maximum on  , that is, there exists an
, that is, there exists an  such that
such that  for all
for all  .
.
Proof.
Let  be equipped with the weak topology. Then, by the Hahn-Banach theorem,
be equipped with the weak topology. Then, by the Hahn-Banach theorem,  is still u.s.c. because
is still u.s.c. because  is quasiconcave, and
is quasiconcave, and  is still closed. Being bounded,
is still closed. Being bounded,  is contained in some closed ball which is weakly compact. Since any closed subset of a compact set is compact,
is contained in some closed ball which is weakly compact. Since any closed subset of a compact set is compact,  is (weakly) compact. Now, by Theorem 9.4 for a single family, we have the conclusion.
is (weakly) compact. Now, by Theorem 9.4 for a single family, we have the conclusion.
Corollary 9.8 is due to Mazur and Schauder in 1936. Some generalized forms of Corollary 9.8 were known by Park et al. [62, 63].
For  , Theorem 9.4 reduces to Corollary 5.5 as follows.
, Theorem 9.4 reduces to Corollary 5.5 as follows.
Proof of Corollary 5.5 from Theorem 9.4.
Let  and
and  . Then all of the requirements of Theorem 9.4 are satisfied. Therefore, by Theorem 9.4, there exists a point
. Then all of the requirements of Theorem 9.4 are satisfied. Therefore, by Theorem 9.4, there exists a point  such that
such that

Therefore, we have


Hence

Therefore

This implies that

On the other hand, we have trivially

and hence

Therefore, we have the conclusion.
10. Historical Remarks on Related Results
-
(I)
As we have seen in Sections 1–3, we have three methods in our subject as follows:
-
(1)
fixed point method—applications of the Kakutani theorem and its various generalizations (e.g., acyclic-valued multimaps, admissible maps, or better admissible maps in the sense of Park); see [3–8, 10, 12, 14–16, 19, 20, 23, 28, 42, 53, 64–68] and others,
-
(2)
continuous selection method—applications of the fact that Fan-Browder-type maps have continuous selections under certain assumptions like Hausdorffness and compactness of relevant spaces; see [17, 22, 36, 39, 40, 58, 69, 70] and others,
-
(3)
the KKM method—as for the Sion theorem, direct applications of the KKM theorem, or its equivalents like the Fan-Browder fixed point theorem for which we do not need the Hausdorffness; see [9, 11, 17, 21, 24–27, 30, 31, 33, 35–37, 39, 43, 45, 47–50, 54, 55, 57, 59, 71, 72] and others.
For Case (1), we will study it elsewhere and, in this paper, we are mainly concerned with Cases  and
and 
-
(II)
An upper semicontinuous (u.s.c.) multimap with nonempty compact convex values is called a Kakutani map. The Fan-Glicksberg theorem was extended by Himmelberg [8] in 1972 for compact Kakutani maps instead of assuming compactness of domains. In 1990, Lassonde [67] extended the Himmelberg theorem to multimaps factorizable by Kakutani maps through convex sets in Hausdorff topological vector spaces. Moreover, Lassonde applied his theorem to game theory and obtained a von Neumann-type intersection theorem for finite number of sets and a Nash-type equilibrium theorem comparable to Debreu's social equilibrium existence theorem [66].
Fixed point theorems extending the Kakutani theorem can be applied to particular forms of results in this paper. Since such extended theorems usually assume Hausdorffness and certain (abstract) local convexity of the related space, their applicability is restrictive.
-
(III)
In 1946, the Kakutani theorem was extended for acyclic maps by Eilenberg and Montgomery [73]. This result was applied by Debreu [66] to the social equilibrium existence theorem and related results.
-
(IV)
Since 1996 [72], many authors have published some results of the present paper for hyperconvex metric spaces. For example, Kirk et al. in 2000 [32] established the KKM theorem, its equivalent formulations, fixed point theorems, and the Nash theorem for hyperconvex metric spaces. However, already in 1993, Horvath [37] found that hyperconvex metric spaces are a particular type of
 -spaces.
-spaces. -
(V)
In 1998 [16], an acyclic version of the social equilibrium existence theorem of Debreu is obtained. This is applied to deduce acyclic versions of theorems on saddle points, minimax theorems, and the following Nash equilibrium theorem.
Corollary 10.1 (see [16]).
Let  be a family of acyclic polyhedra,
be a family of acyclic polyhedra,  , and for each
, and for each  ,
,  a continuous function such that
a continuous function such that
(0)for each  and each
and each  , the set
, the set

is empty or acyclic.
Then there exists a point  such that
such that

-
(VI)
In the present paper, for abstract convex spaces, we notice that the partial KKM principle
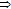 the Fan-Browder fixed point theorem
the Fan-Browder fixed point theorem  the Nash equilibrium theorem, with or without additional intermediate steps. This procedure can be called "from the KKM principle to the Nash equilibria" (simply, "K to N"); see [27].
the Nash equilibrium theorem, with or without additional intermediate steps. This procedure can be called "from the KKM principle to the Nash equilibria" (simply, "K to N"); see [27].
In 1999 [17], we obtained a "K to N" for  -convex spaces. These results extended and unified a number of known results for particular types of
-convex spaces. These results extended and unified a number of known results for particular types of  -convex spaces; see also [18–21, 42]. Therefore, the procedure also holds for Lassonde type-convex spaces, Horvath's
-convex spaces; see also [18–21, 42]. Therefore, the procedure also holds for Lassonde type-convex spaces, Horvath's  -space, hyperconvex metric spaces, and others.
-space, hyperconvex metric spaces, and others.
-
(VII)
In 2000 [20] and 2002 [23], we applied our fixed point theorem for compact compositions of acyclic maps on admissible (in the sense of Klee) convex subsets of a t.v.s. to obtain a cyclic coincidence theorem for acyclic maps, generalized von Neumann-type intersection theorems, the Nash type equilibrium theorems, and the von Neumann minimax theorem.
The following examples are generalized forms of quasi equilibrium theorem or social equilibrium existence theorems which directly imply generalizations of the Nash-Ma-type equilibrium existence theorem.
Theorem 10.2 (see [20]).
Let  be a family of convex sets, each in a t.v.s.
be a family of convex sets, each in a t.v.s.  ,
,  a nonempty compact subset of
a nonempty compact subset of  ,
,  a closed map, and
a closed map, and  u.s.c. functions for each
u.s.c. functions for each  .
.
Suppose that, for each  ,
,
(i) for each
for each  ,
,
(ii)the function  defined on
defined on  by
by

is l.s.c., and
(iii)for each  , the set
, the set

is acyclic.
If  is admissible in
is admissible in  , then there exists an
, then there exists an  such that, for each
such that, for each  ,
,

Theorem 10.3 (see [23]).
Let  be a topological space and let
be a topological space and let  be a family of convex sets, each in a t.v.s.
be a family of convex sets, each in a t.v.s.  . For each
. For each  , let
, let  be a closed map with compact values, and
be a closed map with compact values, and  u.s.c. real-valued functions.
u.s.c. real-valued functions.
Suppose that, for each  ,
,
(i) for each
for each  ,
,
(ii)the function  defined by
defined by

is l.s.c., and
(iii)for each  , the set
, the set

is acyclic.
If  is admissible in
is admissible in  and if all the maps
and if all the maps  are compact except possibly
are compact except possibly  and
and  is u.s.c., then there exists an equilibrium point
is u.s.c., then there exists an equilibrium point  , that is,
, that is,

The following are particular results of ours for  -convex spaces or KKM spaces.
-convex spaces or KKM spaces.
-
(VIII)
In 2001 [22], we obtained generalized forms of the von Neumann-Sion-type minimax theorem, the Fan-Ma intersection theorem, the Fan-Ma type analytic alternative, and the Nash-Ma-equilibrium theorem for
 -convex spaces. In [22], all
-convex spaces. In [22], all  -convex spaces were assumed to be Hausdorff because the results are based on a selection theorem in [40], where Hausdorffness was indispensable.
-convex spaces were assumed to be Hausdorff because the results are based on a selection theorem in [40], where Hausdorffness was indispensable.
As we have seen already in Theorems 7.3, 8.3, 9.2, and 9.6, results following the selection theorem in [40] hold for arbitrary family of Hausdorff  -convex spaces. But corresponding results following the partial KKM principle hold for finite families of abstract convex spaces. At present, we have no way to unify these three cases, namely,
-convex spaces. But corresponding results following the partial KKM principle hold for finite families of abstract convex spaces. At present, we have no way to unify these three cases, namely,  fixed point method,
fixed point method,  selection method, and
selection method, and  KKM method.
KKM method.
-
(IX)
In 2001, for any topological semilattice
 with path-connected interval introduced by Horvath and Llinares [39], the KKM theorem, the Fan-Browder theorem, and the Nash theorem are shown by Luo [33]. Note that such semilattice is known to be a
with path-connected interval introduced by Horvath and Llinares [39], the KKM theorem, the Fan-Browder theorem, and the Nash theorem are shown by Luo [33]. Note that such semilattice is known to be a  -convex space.
-convex space. -
(X)
Cain and González [71] considered relationship among some subclasses of the class of
 -convex spaces and introduced a subclass of the so-called
-convex spaces and introduced a subclass of the so-called  -spaces. In 2007, González et al. [31] repeated to show that
-spaces. In 2007, González et al. [31] repeated to show that  -convex spaces and
-convex spaces and  -spaces satisfy the partial KKM principle. They added that
-spaces satisfy the partial KKM principle. They added that  -spaces satisfy the properties of the Fan type minimax inequality, Fan-Browder-type fixed point, and the Nash-type equilibrium. All of such results are already known for more general
-spaces satisfy the properties of the Fan type minimax inequality, Fan-Browder-type fixed point, and the Nash-type equilibrium. All of such results are already known for more general  -convex spaces.
-convex spaces. -
(XI)
In 2008, Kulpa and Szymanski [45] introduced a series of theorems called Infimum Principles in simplicial spaces. As for applications, they derive fixed point theorems due to Schauder, Tychnoff, Kakutani, and Fan-Browder: minimax theorems, the Nash equilibrium theorem, the Gale-Nikaido-Debreu theorem, and the Ky Fan minimax inequality. Their study is based on and utilizes the techniques of simplicial structure and the Fan-Browder map. Recall that for any abstract convex spaces satisfying abstract KKM principle we can deduce such classical theorems without using any Infimum Principles. Moreover, we note that the newly defined
 -spaces in [45] are particular types of abstract convex spaces satisfying the abstract KKM principle.
-spaces in [45] are particular types of abstract convex spaces satisfying the abstract KKM principle. -
(XII)
In 2008, for
 -spaces, Briec and Horvath [30] showed that some theorems mentioned in this paper hold, that is, Fan-Browder fixed point theorem, Himmelberg-type (in fact, Browder-type and Kakutani-type) fixed point theorems, Fan type minimax inequality, existence of Nash equilibria, and others. Note that
-spaces, Briec and Horvath [30] showed that some theorems mentioned in this paper hold, that is, Fan-Browder fixed point theorem, Himmelberg-type (in fact, Browder-type and Kakutani-type) fixed point theorems, Fan type minimax inequality, existence of Nash equilibria, and others. Note that 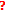 -spaces are KKM spaces [30, Corollary 2.2], and their authors depend the Pelegs type multiple KKM theorem.
-spaces are KKM spaces [30, Corollary 2.2], and their authors depend the Pelegs type multiple KKM theorem. -
(XIII)
Finally, recall that there are several hundred published works on the KKM theory and we can cover only a part of them. For more historical background for the related fixed point theory and for more involved or related results in this paper, see the references [24–27, 41, 43, 48] and the literature therein.
References
von Neumann J: Zur theorie der gesellschaftsspiele. Mathematische Annalen 1928,100(1):295–320. 10.1007/BF01448847
von Neumann J: Über ein ökonomisches Gleichungssystem und eine Verallgemeinerung des Brouwerschen Fixpunktsatzes. Ergebnisse eines Mathematischen Kolloquiums 1937, 8: 73–83.
Kakutani S: A generalization of Brouwer's fixed point theorem. Duke Mathematical Journal 1941, 8: 457–459. 10.1215/S0012-7094-41-00838-4
Nash JF Jr.: Equilibrium points in -person games. Proceedings of the National Academy of Sciences of the United States of America 1950, 36: 48–49. 10.1073/pnas.36.1.48
Nash J: Non-cooperative games. Annals of Mathematics 1951, 54: 286–295. 10.2307/1969529
Fan K: Fixed-point and minimax theorems in locally convex topological linear spaces. Proceedings of the National Academy of Sciences of the United States of America 1952, 38: 121–126. 10.1073/pnas.38.2.121
Glicksberg IL: A further generalization of the Kakutani fixed theorem, with application to Nash equilibrium points. Proceedings of the American Mathematical Society 1952, 3: 170–174.
Himmelberg CJ: Fixed points of compact multifunctions. Journal of Mathematical Analysis and Applications 1972, 38: 205–207. 10.1016/0022-247X(72)90128-X
Fan K: A generalization of Tychonoff's fixed point theorem. Mathematische Annalen 1961, 142: 305–310. 10.1007/BF01353421
Fan K: Sur un théorème minimax. Comptes Rendus des Séances de l'Académie des Sciences. Série I 1964, 259: 3925–3928.
Fan K: Applications of a theorem concerning sets with convex sections. Mathematische Annalen 1966, 163: 189–203. 10.1007/BF02052284
Ma T: On sets with convex sections. Journal of Mathematical Analysis and Applications 1969, 27: 413–416. 10.1016/0022-247X(69)90058-4
Granas A: Sur quelques méthodes topologiques én analyse convexe. In Méthodes Topologiques en Analyse Convexe. Volume 110. Presses Université de Montréal, Montreal, Canada; 1990:11–77.
Idzik A, Park S: Leray-Schauder type theorems and equilibrium existence theorems. In Differential Inclusions and Optimal Control, Lecture Notes in Nonlinear Analysis. Volume 2. University in Toruń, Toruń, Poland; 1998:191–197.
Park S: Applications of the Idzik fixed point theorem. Nonlinear Functional Analysis and Its Applications 1996, 1: 21–56.
Park S: Remarks on a social equilibrium existence theorem of G. Debreu. Applied Mathematics Letters 1998,11(5):51–54. 10.1016/S0893-9659(98)00079-2
Park S: Minimax theorems and the Nash equilibria on generalized convex spaces. In NLA98: Convex Analysis and Chaos, Josai Mathematical Monographs. Volume 1. Josai University, Sakado, Japan; 1999:33–45.
Park S: Elements of the KKM theory for generalized convex spaces. The Korean Journal of Computational & Applied Mathematics 2000,7(1):1–28.
Park S: Fixed points, intersection theorems, variational inequalities, and equilibrium theorems. International Journal of Mathematics and Mathematical Sciences 2000,24(2):73–93. 10.1155/S0161171200002593
Park S: Acyclic versions of the von Neumann and Nash equilibrium theorems. Journal of Computational and Applied Mathematics 2000,113(1–2):83–91. 10.1016/S0377-0427(99)00246-0
Park S: New topological versions of the Fan-Browder fixed point theorem. Nonlinear Analysis: Theory, Methods & Applications 2001,47(1):595–606. 10.1016/S0362-546X(01)00204-8
Park S: Generalizations of the Nash equilibrium theorem on generalized convex spaces. Journal of the Korean Mathematical Society 2001,38(4):697–709.
Park S: Remarks on acyclic versions of generalized von Neumann and Nash equilibrium theorems. Applied Mathematics Letters 2002,15(5):641–647. 10.1016/S0893-9659(02)80018-0
Park S: Elements of the KKM theory on abstract convex spaces. Journal of the Korean Mathematical Society 2008,45(1):1–27.
Park S: Equilibrium existence theorems in KKM spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4352–5364. 10.1016/j.na.2007.10.058
Park S: New foundations of the KKM theory. Journal of Nonlinear and Convex Analysis 2008,9(3):331–350.
Park S: From the KKM principle to the Nash equilibria. International Journal of Mathematics and Statistics 2010,6(S10):77–88.
Park S, Park JA: The Idzik type quasivariational inequalities and noncompact optimization problems. Colloquium Mathematicum 1996,71(2):287–295.
Bielawski R: Simplicial convexity and its applications. Journal of Mathematical Analysis and Applications 1987,127(1):155–171. 10.1016/0022-247X(87)90148-X
Briec W, Horvath C: Nash points, Ky Fan inequality and equilibria of abstract economies in Max-Plus and -convexity. Journal of Mathematical Analysis and Applications 2008,341(1):188–199. 10.1016/j.jmaa.2007.09.056
González L, Kilmer S, Rebaza J: From a KKM theorem to Nash equilibria in -spaces. Topology and Its Applications 2007,155(3):165–170. 10.1016/j.topol.2007.10.003
Kirk WA, Sims B, Yuan GX-Z: The Knaster-Kuratowski and Mazurkiewicz theory in hyperconvex metric spaces and some of its applications. Nonlinear Analysis: Theory, Methods & Applications 2000,39(5):611–627. 10.1016/S0362-546X(98)00225-9
Luo Q: KKM and Nash equilibria type theorems in topological ordered spaces. Journal of Mathematical Analysis and Applications 2001,264(2):262–269. 10.1006/jmaa.2001.7624
Knaster B, Kuratowski K, Mazurkiewicz S: Ein beweis des fixpunktsatzes für n-dimensionale simplexe. Fundamenta Mathematicae 1929, 14: 132–137.
Lassonde M: On the use of KKM multifunctions in fixed point theory and related topics. Journal of Mathematical Analysis and Applications 1983,97(1):151–201. 10.1016/0022-247X(83)90244-5
Horvath CD: Contractibility and generalized convexity. Journal of Mathematical Analysis and Applications 1991,156(2):341–357. 10.1016/0022-247X(91)90402-L
Horvath CD: Extension and selection theorems in topological spaces with a generalized convexity structure. Toulouse Annales Faculté des Sciences 1993,2(2):253–269. 10.5802/afst.766
Reich S, Shafrir I: Nonexpansive iterations in hyperbolic spaces. Nonlinear Analysis: Theory, Methods & Applications 1990,15(6):537–558. 10.1016/0362-546X(90)90058-O
Horvath CD, Llinares Ciscar JV: Maximal elements and fixed points for binary relations on topological ordered spaces. Journal of Mathematical Economics 1996,25(3):291–306. 10.1016/0304-4068(95)00732-6
Park S: Continuous selection theorems in generalized convex spaces. Numerical Functional Analysis and Optimization 1999,20(5–6):567–583. 10.1080/01630569908816911
Park S: Ninety years of the Brouwer fixed point theorem. Vietnam Journal of Mathematics 1999,27(3):187–222.
Park S: Fixed points of better admissible maps on generalized convex spaces. Journal of the Korean Mathematical Society 2000,37(6):885–899.
Park S: Generalized convex spaces, -spaces, and -spaces. Journal of Global Optimization 2009,45(2):203–210. 10.1007/s10898-008-9363-1
Khanh PQ, Quan NH, Yao J-C: Generalized KKM-type theorems in GFC-spaces and applications. Nonlinear Analysis: Theory, Methods & Applications 2009,71(3–4):1227–1234. 10.1016/j.na.2008.11.055
Kulpa W, Szymanski A: Applications of general infimum principles to fixed-point theory and game theory. Set-Valued Analysis 2008,16(4):375–398. 10.1007/s11228-007-0055-7
Kirk WA, Panyanak B: Best approximation in -trees. Numerical Functional Analysis and Optimization 2007,28(5–6):681–690. 10.1080/01630560701348517
Horvath CD: Topological convexities, selections and fixed points. Topology and Its Applications 2008,155(8):830–850. 10.1016/j.topol.2007.01.024
Park S: Remarks on the partial KKM principle. Nonlinear Analysis Forum 2009, 14: 51–62.
Fan K: A minimax inequality and applications. In Inequalities, III. Edited by: Shisha O. Academic Press, New York, NY, USA; 1972:103–113.
Cho YJ, Kim JK, Lee BY: Remarks on KKM maps and applications. The Journal of Advanced Research in Applied Mathematics 2009,1(1):1–8.
Liu FC: A note on the von Neumann-Sion minimax principle. Bulletin of the Institute of Mathematics. Academia Sinica 1978,6(2, part 2):517–524.
Shih MH, Tan K-K: Noncompact sets with convex sections. II. Journal of Mathematical Analysis and Applications 1986,120(1):264–270. 10.1016/0022-247X(86)90214-3
Nikaidô H: On von Neumann's minimax theorem. Pacific Journal of Mathematics 1954, 4: 65–72.
Sion M: On general minimax theorems. Pacific Journal of Mathematics 1958, 8: 171–176.
Komiya H: Convexity on a topological space. Fundamenta Mathematicae 1981,111(2):107–113.
Park S: Foundations of the KKM theory via coincidences of composites of upper semicontinuous maps. Journal of the Korean Mathematical Society 1994,31(3):493–519.
Simons S: Two-function minimax theorems and variational inequalities for functions on compact and noncompact sets, with some comments on fixed-point theorems. In Nonlinear Functional Analysis and Its Applications, Part 2, Proceedings of Symposia in Pure Mathematics. Volume 45. American Mathematical Society, Providence, RI, USA; 1986:377–392.
Tarafdar E: Fixed point theorems in -spaces and equilibrium points of abstract economies. Journal of Australian Mathematical Society 1992,53(2):252–260. 10.1017/S1446788700035825
Chang SY: A generalization of KKM principle and its applications. Soochow Journal of Mathematics 1989,15(1):7–17.
Nikaidô H, Isoda K: Note on non-cooperative convex games. Pacific Journal of Mathematics 1955, 5: 807–815.
Tan K-K, Yu J, Yuan X-Z: Existence theorems of Nash equilibria for non-cooperative -person games. International Journal of Game Theory 1995,24(3):217–222. 10.1007/BF01243152
Park S: Variational inequalities and extremal principles. Journal of the Korean Mathematical Society 1991,28(1):45–56.
Park S, Kim SK: On generalized extremal principles. Bulletin of the Korean Mathematical Society 1990,27(1):49–52.
Bohnenblust HF, Karlin S: On a theorem of Ville. In Contributions to the Theory of Games, Annals of Mathematics Studies, no. 24. Princeton University Press, Princeton, NJ, USA; 1950:155–160.
Dantzig GB: Constructive proof of the min-max theorem. Pacific Journal of Mathematics 1956, 6: 25–33.
Debreu G: A social equilibrium existence theorem. Proceedings of the National Academy of Sciences of the United States of America 1952, 38: 886–893. 10.1073/pnas.38.10.886
Lassonde M: Fixed points for Kakutani factorizable multifunctions. Journal of Mathematical Analysis and Applications 1990,152(1):46–60. 10.1016/0022-247X(90)90092-T
Torres-Martínez JP: Fixed points as Nash equilibria. Fixed Point Theory and Applications 2006, 2006:-4.
Ben-El-Mechaiekh H, Deguire P, Granas A: Une alternative non linéaire en analyse convexe et applications. Comptes Rendus des Séances de l'Académie des Sciences. Série I 1982,295(3):257–259.
Browder FE: The fixed point theory of multi-valued mappings in topological vector spaces. Mathematische Annalen 1968, 177: 283–301. 10.1007/BF01350721
Cain GL Jr., González L: The Knaster-Kuratowski-Mazurkiewicz theorem and abstract convexities. Journal of Mathematical Analysis and Applications 2008,338(1):563–571. 10.1016/j.jmaa.2007.05.050
Khamsi MA: KKM and Ky Fan theorems in hyperconvex metric spaces. Journal of Mathematical Analysis and Applications 1996,204(1):298–306. 10.1006/jmaa.1996.0438
Eilenberg S, Montgomery D: Fixed point theorems for multi-valued transformations. American Journal of Mathematics 1946, 68: 214–222. 10.2307/2371832
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, S. Generalizations of the Nash Equilibrium Theorem in the KKM Theory. Fixed Point Theory Appl 2010, 234706 (2010). https://doi.org/10.1155/2010/234706
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/234706
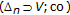 is given for the original KKM theorem [
is given for the original KKM theorem [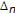 is the standard
is the standard  -simplex,
-simplex,  is the set of its vertices
is the set of its vertices  , and co:
, and co:  is the convex hull operation.
is the convex hull operation. is given, where
is given, where 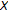 and
and 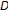 are subsets of a t.v.s.
are subsets of a t.v.s. 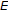 such that co
such that co  and
and  co. Fan's celebrated KKM lemma [
co. Fan's celebrated KKM lemma [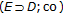 .
.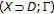 is a triple where
is a triple where 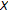 is a subset of a vector space such that co
is a subset of a vector space such that co 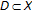 , and each
, and each  is the convex hull of
is the convex hull of 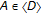 equipped with the Euclidean topology. This concept generalizes the one due to Lassonde for
equipped with the Euclidean topology. This concept generalizes the one due to Lassonde for 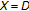 ; see [
; see [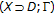 .
. is called an
is called an 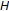 -space if
-space if  is a topological space and
is a topological space and 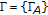 is a family of contractible (or, more generally,
is a family of contractible (or, more generally,  -connected) subsets of
-connected) subsets of 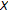 indexed by
indexed by  such that
such that 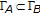 whenever
whenever  . If
. If  , then
, then  is called a
is called a  -space by Horvath [
-space by Horvath [ -spaces; see [
-spaces; see [ -spaces. This class of metric spaces contains all normed vector spaces, all Hadamard manifolds, the Hilbert ball with the hyperbolic metric, and others. Note that an arbitrary product of hyperbolic spaces is also hyperbolic.
-spaces. This class of metric spaces contains all normed vector spaces, all Hadamard manifolds, the Hilbert ball with the hyperbolic metric, and others. Note that an arbitrary product of hyperbolic spaces is also hyperbolic.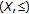 with path-connected interval is introduced by Horvath and Llinares [
with path-connected interval is introduced by Horvath and Llinares [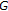 -convex space
-convex space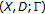 due to Park is an abstract convex space such that for each
due to Park is an abstract convex space such that for each 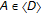 with the cardinality
with the cardinality 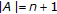 there exists a continuous function
there exists a continuous function 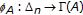 such that
such that 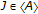 implies that
implies that  .
. -space
-space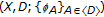 consists of a topological space
consists of a topological space 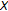 , a nonempty set
, a nonempty set 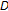 , and a family of continuous functions
, and a family of continuous functions  (that is, singular
(that is, singular  -simplexes) for
-simplexes) for 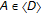 with
with 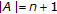 . Every
. Every  -space can be made into a
-space can be made into a  -convex space; see [
-convex space; see [ -spaces are called
-spaces are called 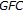 -spaces in [
-spaces in [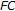 -spaces [
-spaces [ .
. is a closed convex subset of a complete
is a closed convex subset of a complete  -tree
-tree 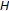 , and for each
, and for each  ,
, 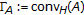 , where
, where 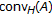 is the intersection of all closed convex subsets of
is the intersection of all closed convex subsets of 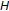 that contain
that contain  ; see Kirk and Panyanak [
; see Kirk and Panyanak [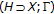 is an abstract convex space.
is an abstract convex space. with a convexity in the sense of Horvath [
with a convexity in the sense of Horvath [ -space due to Briec and Horvath [
-space due to Briec and Horvath [ -convex space is a KKM space [
-convex space is a KKM space [ can be made into a KKM space [
can be made into a KKM space [ is a KKM space
is a KKM space  with the ordinal space
with the ordinal space  ; see [
; see [ is not a
is not a  -convex space.
-convex space. of a complete
of a complete  -tree
-tree 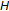 , and
, and 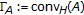 for each
for each 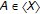 , the triple
, the triple  satisfies the partial KKM principle; see [
satisfies the partial KKM principle; see [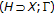 is a KKM space [
is a KKM space [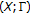 with the weak Van de Vel property is a KKM space, where
with the weak Van de Vel property is a KKM space, where 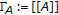 for each
for each 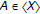 ; see [
; see [ -space due to Briec and Horvath [
-space due to Briec and Horvath [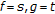 , Corollary 5.3 reduces to [
, Corollary 5.3 reduces to [ and
and  are compact convex spaces in the sense of Komiya.
are compact convex spaces in the sense of Komiya. ,
, 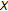 is a convex space, and
is a convex space, and  , then Theorem 6.1 reduces to the well-known Fan-Browder fixed point theorem; see Park [
, then Theorem 6.1 reduces to the well-known Fan-Browder fixed point theorem; see Park [ , Theorem 6.1 for a convex space
, Theorem 6.1 for a convex space 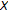 was obtained by Ben-El-Mechaiekh et al. [
was obtained by Ben-El-Mechaiekh et al. [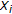 are convex subsets of t.v.s. and
are convex subsets of t.v.s. and  for all
for all 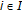 .
.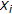 are convex spaces.
are convex spaces.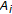 and
and  .
.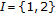 , Theorems 8.1 and 8.3 imply the Fan minimax inequality.
, Theorems 8.1 and 8.3 imply the Fan minimax inequality. -spaces.
-spaces. the Fan-Browder fixed point theorem
the Fan-Browder fixed point theorem  the Nash equilibrium theorem, with or without additional intermediate steps. This procedure can be called "from the KKM principle to the Nash equilibria" (simply, "K to N"); see [
the Nash equilibrium theorem, with or without additional intermediate steps. This procedure can be called "from the KKM principle to the Nash equilibria" (simply, "K to N"); see [ -convex spaces. In [
-convex spaces. In [ -convex spaces were assumed to be Hausdorff because the results are based on a selection theorem in [
-convex spaces were assumed to be Hausdorff because the results are based on a selection theorem in [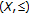 with path-connected interval introduced by Horvath and Llinares [
with path-connected interval introduced by Horvath and Llinares [ -convex space.
-convex space. -convex spaces and introduced a subclass of the so-called
-convex spaces and introduced a subclass of the so-called  -spaces. In 2007, González et al. [
-spaces. In 2007, González et al. [ -convex spaces and
-convex spaces and  -spaces satisfy the partial KKM principle. They added that
-spaces satisfy the partial KKM principle. They added that  -spaces satisfy the properties of the Fan type minimax inequality, Fan-Browder-type fixed point, and the Nash-type equilibrium. All of such results are already known for more general
-spaces satisfy the properties of the Fan type minimax inequality, Fan-Browder-type fixed point, and the Nash-type equilibrium. All of such results are already known for more general  -convex spaces.
-convex spaces. -spaces in [
-spaces in [ -spaces, Briec and Horvath [
-spaces, Briec and Horvath [ -spaces are KKM spaces [
-spaces are KKM spaces [