- Research Article
- Open access
- Published:
Nonlinear Contractive Conditions for Coupled Cone Fixed Point Theorems
Fixed Point Theory and Applications volume 2010, Article number: 190606 (2010)
Abstract
We establish some new coupled fixed point theorems for various types of nonlinear contractive maps in the setting of quasiordered cone metric spaces which not only obtain several coupled fixed point theorems announced by many authors but also generalize them under weaker assumptions.
1. Introduction
The existence of fixed point in partially ordered sets has been studied and investigated recently in [1–13] and references therein. Since the various contractive conditions are important in metric fixed point theory, there is a trend to weaken the requirement on contractions. Nieto and Rodríguez-López in [8, 10] used Tarski's theorem to show the existence of solutions for fuzzy equations and fuzzy differential equations, respectively. The existence of solutions for matrix equations or ordinary differential equations by applying fixed point theorems are presented in [2, 6, 9, 11, 12]. In [3, 13], the authors proved some fixed point theorems for a mixed monotone mapping in a metric space endowed with partial order and applied their results to problems of existence and uniqueness of solutions for some boundary value problems.
In 2006, Bhaskar and Lakshmikantham [2] first proved the following interesting coupled fixed point theorem in partially ordered metric spaces.
Theorem BL. (Bhaskar and Lakshmikantham).
Let  be a partially ordered set and
be a partially ordered set and  a metric on
a metric on  such that
such that  is a complete metric space. Let
is a complete metric space. Let  be a continuous mapping having the mixed monotone property on
be a continuous mapping having the mixed monotone property on  . Assume that there exists a
. Assume that there exists a 
 with
with

If there exist  such that
such that  and
and  , then, there exist
, then, there exist  , such that
, such that  and
and  .
.
Let  be a topological vector space (t.v.s. for short) with its zero vector
be a topological vector space (t.v.s. for short) with its zero vector  . A nonempty subset
. A nonempty subset  of
of  is called a convex cone if
is called a convex cone if  and
and  for
for  . A convex cone
. A convex cone  is said to be
is said to be  if
if  . For a given proper, pointed, and convex cone
. For a given proper, pointed, and convex cone  in
in  , we can define a partial ordering
, we can define a partial ordering  with respect to
with respect to  by
by

 will stand for
will stand for  and
and  while
while  will stand for
will stand for  , where
, where  denotes the interior of
denotes the interior of  .
.
In the following, unless otherwise specified, we always assume that  is a locally convex Hausdorff t.v.s. with its zero vector
is a locally convex Hausdorff t.v.s. with its zero vector  ,
,  a proper, closed, convex, and pointed cone in
a proper, closed, convex, and pointed cone in  with
with  ,
,  a partial ordering with respect to
a partial ordering with respect to  , and
, and  .
.
Very recently, Du [14] first introduced the concepts of  -cone metric and
-cone metric and  -cone metric space to improve and extend the concept of cone metric space in the sense of Huang and Zhang [15].
-cone metric space to improve and extend the concept of cone metric space in the sense of Huang and Zhang [15].
Definition 1.1 . (see [14]).
Let  be a nonempty set. A vector-valued function
be a nonempty set. A vector-valued function  is said to be a
is said to be a  -cone metric if the following conditions hold:
-cone metric if the following conditions hold:
(C1) for all
for all 
 and
and  if and only if
if and only if  ;
;
(C2) for all
for all 
 ;
;
(C3) for all
for all  .
.
The pair  is then called a
is then called a  -cone metric space.
-cone metric space.
Definition 1.2 . (see [14]).
Let  be a
be a  -cone metric space,
-cone metric space,  , and
, and  a sequence in
a sequence in  .
.
(i) is said to
is said to  -cone converge to
-cone converge to if for every
if for every  with
with  there exists a natural number
there exists a natural number  such that
such that  for all
for all  . We denote this by cone-
. We denote this by cone- or
or  as
as  and call
and call  the
the  -cone limit of
-cone limit of  .
.
(ii) is said to be a
is said to be a  -cone Cauchy sequence if for every
-cone Cauchy sequence if for every  with
with  there is a natural number
there is a natural number  such that
such that  for all
for all  ,
,  .
.
(iii) is said to be
is said to be  -cone complete if every
-cone complete if every  -cone Cauchy sequence in
-cone Cauchy sequence in  is
is  -cone convergent in
-cone convergent in  .
.
In [14], the author proved the following important results.
Theorem 1.3 . (see [14]).
Let  be a
be a  -cone metric space. Then
-cone metric space. Then  defined by
defined by  is a metric, where
is a metric, where  is defined by
is defined by

Theorem 1.4 . (see [14]).
Let  be a
be a  -cone metric space,
-cone metric space,  , and
, and  a sequence in
a sequence in  . Then the following statements hold:
. Then the following statements hold:
(a)if  -cone converges to
-cone converges to  (i.e.,
(i.e.,  as
as  , then
, then  as
as  (i.e.,
(i.e.,  as
as  ;
;
(b)if  is a
is a  -cone Cauchy sequence in
-cone Cauchy sequence in  , then
, then  is a Cauchy sequence (in usual sense) in
is a Cauchy sequence (in usual sense) in  .
.
In this paper, we establish some new coupled fixed point theorems for various types of nonlinear contractive maps in the setting of quasiordered cone metric spaces. Our results generalize and improve some results in [2, 4, 9, 11] and references therein.
2. Preliminaries
Let  be a nonempty set and "
be a nonempty set and " " a quasiorder (preorder or pseudoorder, i.e., a reflexive and transitive relation) on
" a quasiorder (preorder or pseudoorder, i.e., a reflexive and transitive relation) on  . Then
. Then  is called a quasiordered set. A sequence
is called a quasiordered set. A sequence  is called
is called  -nondecreasing (resp.,
-nondecreasing (resp.,  -nonincreasing) if
-nonincreasing) if  (resp.,
(resp.,  ) for each
) for each  . In this paper, we endow the product space
. In this paper, we endow the product space  with the following quasiorder
with the following quasiorder  :
:

Recall that the nonlinear scalarization function  is defined by
is defined by

Theorem 2.1 . (see [14, 16, 17]).
For each  and
and  , the following statements are satisfied:
, the following statements are satisfied:
(i)

 ;
;
(ii)

 ;
;
(iii)

 ;
;
(iv)

 ;
;
(v) is positively homogeneous and continuous on
is positively homogeneous and continuous on  ;
;
(vi)if  , then
, then  ;
;
(vii) for all
for all  .
.
Remark 2.2.
-
(a)
Clearly,
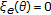 .
. -
(b)
The reverse statement of (vi) in Theorem 2.1 (i.e.,
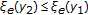
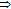
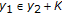 ) does not hold in general. For example, let
) does not hold in general. For example, let  , and
, and 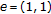 . Then
. Then 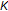 is a proper, closed, convex, and pointed cone in
is a proper, closed, convex, and pointed cone in  with
with  and
and  . For
. For 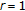 , it is easy to see that
, it is easy to see that 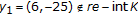 , and
, and 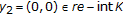 . By applying (iii) and (iv) of Theorem 2.1, we have
. By applying (iii) and (iv) of Theorem 2.1, we have 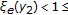
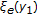 but indeed
but indeed 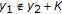 .
.
For any  -cone metric space
-cone metric space  , we can define the map
, we can define the map  by
by

It is obvious that  is also a
is also a  -cone metric on
-cone metric on  , and if
, and if  and
and  as
as  , then
, then  (i.e.,
(i.e.,  TVS-cone converges to
TVS-cone converges to  .
.
By Theorem 1.3, we know that  is a metric on
is a metric on  . Hence the function
. Hence the function  :
:  , defined by
, defined by

is a metric on  .
.
A map  is said to be
is said to be  -continuous at
-continuous at  if any sequence
if any sequence  with
with  implies that
implies that  .
.  is said to be
is said to be  -continuous on
-continuous on  if
if  is continuous at every point of
is continuous at every point of  .
.
Definition 2.3 . (see [2, 4]).
Let  be a quasiordered set and
be a quasiordered set and  a map. one says that
a map. one says that  has the mixed monotone property on
has the mixed monotone property on  if
if  is monotone nondecreasing in
is monotone nondecreasing in  and is monotone nonincreasing in
and is monotone nonincreasing in  , that is, for any
, that is, for any  ,
,  ,
,

Definition 2.4 . (see [2, 4]).
Let  be a nonempty set and
be a nonempty set and  a map. One calls an element
a map. One calls an element  a coupled fixed point of
a coupled fixed point of  if
if

Definition 2.5.
Let  be a
be a  -cone metric space with a quasi-order
-cone metric space with a quasi-order  (
( for short). A nonempty subset
for short). A nonempty subset  of
of  is said to be
is said to be
(i) -cone sequentially
-cone sequentially -
- if every
if every  -nondecreasing
-nondecreasing  -cone Cauchy sequence in
-cone Cauchy sequence in  converges,
converges,
(ii) -cone sequentially
-cone sequentially -
- if every
if every  -nonincreasing
-nonincreasing  -cone Cauchy sequence in
-cone Cauchy sequence in  converges,
converges,
(iii) -cone sequentially
-cone sequentially -
- if it is both
if it is both  -cone sequentially
-cone sequentially  -complete and
-complete and  -cone sequentially
-cone sequentially  -
- .
.
Definition 2.6 . (see [4, 18]).
A function 
 is said to be a
is said to be a  -
- if it satisfies Mizoguchi-Takahashi's condition (i.e.,
if it satisfies Mizoguchi-Takahashi's condition (i.e.,  for all
for all  ).
).
Clearly, if  is a nondecreasing function, then
is a nondecreasing function, then  is a
is a  -function. Notice that
-function. Notice that 
 is a
is a  -function if and only if for each
-function if and only if for each  there exist
there exist  and
and  such that
such that  for all
for all  ; for more detail, see [4, Remark
; for more detail, see [4, Remark  (iii)].
(iii)].
Very recently, Du and Wu [5] introduced and studied the concept of functions of contractive factor.
Definition 2.7 . (see [5]).
One says that  is a function of contractive factor if for any strictly decreasing sequence
is a function of contractive factor if for any strictly decreasing sequence  in
in  , one has
, one has

The following result tells us the relationship between  -functions and functions of contractive factor.
-functions and functions of contractive factor.
Theorem 2.8.
Any  -function is a function of contractive factor.
-function is a function of contractive factor.
Proof.
Let  be a
be a  -function, and let
-function, and let  be a strictly decreasing sequence in
be a strictly decreasing sequence in  . Then
. Then  exists. Since
exists. Since  is a
is a  -function, there exist
-function, there exist  and
and  such that
such that  for all
for all  . On the other hand, there exists
. On the other hand, there exists  , such that
, such that

for all  with
with  . Hence
. Hence  for all
for all  . Let
. Let

Then  for all
for all  , and hence
, and hence  . Therefore
. Therefore  is a function of contractive factor.
is a function of contractive factor.
3. Coupled Fixed Point Theorems for Various Types of Nonlinear Contractive Maps
Definition 3.1.
One says that 
 is a function of strong contractive factor if for any strictly decreasing sequence
is a function of strong contractive factor if for any strictly decreasing sequence  in
in  , one has
, one has

It is quite obvious that if  is a function of strong contractive factor, then
is a function of strong contractive factor, then  is a function of contractive factor but the reverse is not always true.
is a function of contractive factor but the reverse is not always true.
The following results are crucial to our proofs in this paper.
Lemma 3.2.
A function of strong contractive factor can be structured by a function of contractive factor.
Proof.
Let  be a function of contractive factor. Define
be a function of contractive factor. Define  ,
,  . We claim that
. We claim that  is a function of strong contractive factor. Clearly,
is a function of strong contractive factor. Clearly,  for all
for all  . Let
. Let  be a strictly decreasing sequence in
be a strictly decreasing sequence in  . Since
. Since  is a function of contractive factor,
is a function of contractive factor,  . Thus it follows that
. Thus it follows that

Hence  is a function of strong contractive factor.
is a function of strong contractive factor.
Lemma 3.3.
Let  be a t.v.s.,
be a t.v.s.,  a convex cone with
a convex cone with  in
in  , and
, and  . Then the following statements hold.
. Then the following statements hold.
(i)If  and
and  , then
, then  ;
;
(ii)If  and
and  , then
, then  ;
;
(iii)If  and
and  , then
, then  .
.
Proof.
To see (i), since the set  is open in
is open in  and
and  is a convex cone, we have
is a convex cone, we have

Since  and
and  , it follows that
, it follows that

which means that  . The proofs of conclusions (ii) and(iii) are similar to (i).
. The proofs of conclusions (ii) and(iii) are similar to (i).
Lemma 3.4 (see [4]).
Let  be a quasiordered set and
be a quasiordered set and  a multivalued map having the mixed monotone property on
a multivalued map having the mixed monotone property on  . Let
. Let  . Define two sequences
. Define two sequences  and
and  by
by

for each  . If
. If  and
and  , then
, then  is
is  -nondecreasing and
-nondecreasing and  is
is  -nonincreasing.
-nonincreasing.
In this section, we first present the following new coupled fixed point theorem for functions of contractive factor in quasiordered cone metric spaces which is one of the main results of this paper.
Theorem 3.5.
Let  be a
be a  -cone sequentially
-cone sequentially  -complete metric space,
-complete metric space,  a map having the mixed monotone property on
a map having the mixed monotone property on  , and
, and  . Assume that there exists a function of contractive factor
. Assume that there exists a function of contractive factor 

 such that for any
such that for any  with
with  ,
,

and there exist  such that
such that  and
and  . Define the iterative sequence
. Define the iterative sequence  in
in  by
by  and
and  for
for  . Then the following statements hold.
. Then the following statements hold.
(a)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(b)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space, where
is a complete metric space, where 
 for any
for any  . Moreover, if
. Moreover, if  is
is  -continuous on
-continuous on  , then
, then  -cone converges to a coupled fixed point in
-cone converges to a coupled fixed point in  of
of  .
.
Proof.
Since  is a locally convex Hausdorff t.v.s. with its zero vector
is a locally convex Hausdorff t.v.s. with its zero vector  , let
, let  denote the topology of
denote the topology of  and let
and let  be the base at
be the base at  consisting of all absolutely convex neighborhood of
consisting of all absolutely convex neighborhood of  . Let
. Let

Then  is a family of seminorms on
is a family of seminorms on  . For each
. For each  , let
, let

and let

Then  is a base at
is a base at  , and the topology
, and the topology  generated by
generated by  is the weakest topology for
is the weakest topology for  such that all seminorms in
such that all seminorms in  are continuous and
are continuous and  . Moreover, given any neighborhood
. Moreover, given any neighborhood  of
of  , there exists
, there exists  such that
such that  (see, e.g., [19, Theorem
(see, e.g., [19, Theorem  in II.12, Page 113]).
in II.12, Page 113]).
By Lemma 3.2, we can define a function of strong contractive factor  by
by  . Then
. Then  for all
for all  . For any
. For any  , let
, let  and
and  . Then, by Lemma 3.4,
. Then, by Lemma 3.4,  is
is  -nondecreasing and
-nondecreasing and  is
is  -nonincreasing. So
-nonincreasing. So  and
and  for each
for each  . By (3.6), we obtain
. By (3.6), we obtain


By (3.10) and Theorem 2.1,

Similarly, by (3.11) and Theorem 2.1, we also have

Combining (3.12) and (3.13), we get

For each  , let
, let  . Then
. Then  . By induction, we can obtain the following. For each
. By induction, we can obtain the following. For each  ,
,





Since  for all
for all  , the sequence
, the sequence  is strictly decreasing in
is strictly decreasing in  from (3.19). Since
from (3.19). Since  is a function of strong contractive factor, we have
is a function of strong contractive factor, we have

So  for all
for all  . We want to prove that
. We want to prove that  is a
is a  -nondecreasing
-nondecreasing  -cone Cauchy sequence and
-cone Cauchy sequence and  is a
is a  -nonincreasing
-nonincreasing  -cone Cauchy sequence in
-cone Cauchy sequence in  . For each
. For each  , by (3.15), we have
, by (3.15), we have

Similarly, by (3.16), we obtain

From (3.21) and (3.22), we get

Hence it follows from (3.21), (3.22), and (3.23) that

Therefore, for  with
with  , we have
, we have


Given  with
with  (i.e.,
(i.e.,  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that  . Therefore, there exists
. Therefore, there exists  with
with  such that
such that  , where
, where

for some  and
and  ,
,  . Let
. Let

If  , since each
, since each  is a seminorm, we have
is a seminorm, we have  and
and

for all  and all
and all  . If
. If  , since
, since 
 ,
,  , and hence there exists
, and hence there exists  such that
such that  for all
for all  . So, for each
. So, for each  and any
and any  , we obtain
, we obtain

Therefore for any  ,
,  for all
for all  , and hence
, and hence  . So we obtain
. So we obtain

or

for all  . For
. For  with
with  , by (3.25), (3.26), (3.32), and Lemma 3.3, we obtain
, by (3.25), (3.26), (3.32), and Lemma 3.3, we obtain

Hence  is a
is a  -nondecreasing
-nondecreasing  -cone Cauchy sequence and
-cone Cauchy sequence and  is a
is a  -nonincreasing
-nonincreasing  -cone Cauchy sequence in
-cone Cauchy sequence in  . By the
. By the  -cone sequential
-cone sequential  -completeness of
-completeness of  , there exist
, there exist  such that
such that 
 -cone converges to
-cone converges to  and
and  -cone converges to
-cone converges to  . Therefore
. Therefore  -cone converges to
-cone converges to  .
.
On the other hand, applying Theorem 1.4, we have the following:




Since  for all
for all  , by (3.36) and (3.37), we have
, by (3.36) and (3.37), we have  as
as  . Let
. Let  ,
,  , and
, and  . Then
. Then  ,
,  , and
, and  are also complete metric spaces. Hence conclusion (a) holds.
are also complete metric spaces. Hence conclusion (a) holds.
Finally, in order to complete the proof of conclusion (b), we need to verify that  is a coupled fixed point of
is a coupled fixed point of  . Let
. Let  be given. Since
be given. Since  is
is  -continuous on
-continuous on  and
and  ,
,  is
is  -continuous at
-continuous at  . So there exists
. So there exists  such that
such that

whenever  with
with  . Since
. Since  and
and  as
as  , for
, for  there exists
there exists  such that
such that

So, for each  with
with  , by (3.39),
, by (3.39),

and hence we have from (3.38) that

Therefore

Since  is arbitrary,
is arbitrary,  or
or  . Similarly, we can also prove that
. Similarly, we can also prove that  . So
. So  is a coupled fixed point of
is a coupled fixed point of  . The proof is finished.
. The proof is finished.
The following conclusions are immediate from Theorems 2.8 and 3.5.
Theorem 3.6.
Let  be a
be a  -cone sequentially
-cone sequentially  -complete metric space,
-complete metric space,  a map having the mixed monotone property on
a map having the mixed monotone property on  , and
, and  . Assume that there exists a
. Assume that there exists a  -function
-function  such that for any
such that for any  with
with  ,
,

and there exist  such that
such that  and
and  . Define the iterative sequence
. Define the iterative sequence  in
in  by
by  and
and  for
for  . Then the following statements hold.
. Then the following statements hold.
(a)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(b)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space. Moreover, if
is a complete metric space. Moreover, if  is
is  -continuous on
-continuous on  , then
, then  -cone converges to a coupled fixed point in
-cone converges to a coupled fixed point in  of
of  .
.
Theorem 3.7.
Let  be a
be a  -cone sequentially
-cone sequentially  -complete metric space,
-complete metric space,  a map having the mixed monotone property on
a map having the mixed monotone property on  , and
, and  . Assume that there exists a nonnegative number
. Assume that there exists a nonnegative number  such that for any
such that for any  with
with  ,
,

and there exist  such that
such that  and
and  . Define the iterative sequence
. Define the iterative sequence  in
in  by
by  and
and  for
for  . Then the following statements hold.
. Then the following statements hold.
(a)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(b)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space. Moreover, if
is a complete metric space. Moreover, if  is
is  -continuous on
-continuous on  , then
, then  -cone converges to a coupled fixed point in
-cone converges to a coupled fixed point in  of
of  .
.
Remark 3.8.
-
(a)
Theorems 3.5 and 3.6 all generalize and improve [4, Theorem
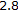 ] and some results in [2, 9, 11].
] and some results in [2, 9, 11]. -
(b)
Theorems 3.5–3.7 all generalize Bhaskar-Lakshmikantham's coupled fixed points theorem (i.e., Theorem BL).
Finally, we focus our research on  -cone metric spaces.
-cone metric spaces.
Theorem 3.9.
Let  be a
be a  -cone complete metric space,
-cone complete metric space,  a map, and
a map, and  . Assume that there exists a function of contractive factor
. Assume that there exists a function of contractive factor  such that for any
such that for any 

Let  . Define the iterative sequence
. Define the iterative sequence  in
in  by
by  and
and  for
for  . Then the following statements hold.
. Then the following statements hold.
(a)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(b)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(c) has a unique coupled fixed point in
has a unique coupled fixed point in  . Moreover,
. Moreover,  -cone converges to the coupled fixed point of
-cone converges to the coupled fixed point of  .
.
Proof.
For any  , by (3.45) and Theorem 2.1, we obtain
, by (3.45) and Theorem 2.1, we obtain

From (3.46), we know that  is
is  -continuous on
-continuous on  . Following the same argument as in the proof of Theorem 3.5, we can prove that conclusions (a) and (b) hold and there exists
. Following the same argument as in the proof of Theorem 3.5, we can prove that conclusions (a) and (b) hold and there exists  , such that
, such that  -cone converges to
-cone converges to  and
and  is a coupled fixed point of
is a coupled fixed point of  . To complete the proof, it suffices to show the uniqueness of the coupled fixed point of
. To complete the proof, it suffices to show the uniqueness of the coupled fixed point of  . On the contrary, suppose that there exists
. On the contrary, suppose that there exists  , such that
, such that  and
and  . By (3.46), we have
. By (3.46), we have

So, it follows from (3.47) that

which leads to a contradiction. The proof is completed.
The following results are immediate from Theorem 3.9.
Theorem 3.10.
Let  be a
be a  -cone complete metric space,
-cone complete metric space,  a map, and
a map, and  . Assume that there exists a
. Assume that there exists a  -function
-function  such that for any
such that for any  ,
,

Let  . Define the iterative sequence
. Define the iterative sequence  in
in  by
by  and
and  for
for  . Then the following statements hold.
. Then the following statements hold.
(a)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(b)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
(c) has a unique coupled fixed point in
has a unique coupled fixed point in  . Moreover,
. Moreover,  -cone converges to the coupled fixed point of
-cone converges to the coupled fixed point of  .
.
Theorem 3.11.
Let  be a
be a  -cone complete metric space and
-cone complete metric space and  a map. Assume that there exists a nonnegative number
a map. Assume that there exists a nonnegative number  such that for any
such that for any  ,
,

Let  . Define the iterative sequence
. Define the iterative sequence  in
in  by
by  and
and  for
for  . Then the following statements hold.
. Then the following statements hold.
(a)There exists a nonempty subset  of
of  , such that
, such that  is a complete metric space.
is a complete metric space.
-
(b)
There exists a nonempty subset
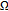 of
of 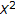 , such that
, such that 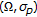 is a complete metric space.
is a complete metric space.
(c) has a unique coupled fixed point in
has a unique coupled fixed point in  . Moreover,
. Moreover,  -cone converges to the coupled fixed point of
-cone converges to the coupled fixed point of  .
.
Remark 3.12.
References
Agarwal RP, El-Gebeily MA, O'Regan D: Generalized contractions in partially ordered metric spaces. Applicable Analysis 2008,87(1):109–116. 10.1080/00036810701556151
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Analysis: Theory, Methods & Applications 2006,65(7):1379–1393. 10.1016/j.na.2005.10.017
Burgić D, Kalabušić S, Kulenović MRS: Global attractivity results for mixed-monotone mappings in partially ordered complete metric spaces. Fixed Point Theory and Applications 2009, 2009:-17.
Du W-S: Coupled fixed point theorems for nonlinear contractions satisfied Mizoguchi-Takahashi's condition in quasiordered metric spaces. Fixed Point Theory and Applications 2010, 2010:-9.
Du W-S, Wu H-C: Fixed point theorems for vectorial elements. submitted
Harjani J, Sadarangani K: Fixed point theorems for weakly contractive mappings in partially ordered sets. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):3403–3410. 10.1016/j.na.2009.01.240
Lakshmikantham V, Ćirić L: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(12):4341–4349. 10.1016/j.na.2008.09.020
Nieto JJ, Rodríguez-López R: Existence of extremal solutions for quadratic fuzzy equations. Fixed Point Theory and Applications 2005,2005(3):321–342. 10.1155/FPTA.2005.321
Nieto JJ, Rodríguez-López R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005,22(3):223–239. 10.1007/s11083-005-9018-5
Nieto JJ, Rodríguez-López R: Applications of contractive-like mapping principles to fuzzy equations. Revista Matemática Complutense 2006,19(2):361–383.
Nieto JJ, Rodríguez-López R: Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Mathematica Sinica 2007,23(12):2205–2212. 10.1007/s10114-005-0769-0
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proceedings of the American Mathematical Society 2004,132(5):1435–1443. 10.1090/S0002-9939-03-07220-4
Wu Y: New fixed point theorems and applications of mixed monotone operator. Journal of Mathematical Analysis and Applications 2008,341(2):883–893. 10.1016/j.jmaa.2007.10.063
Du W-S: A note on cone metric fixed point theory and its equivalence. Nonlinear Analysis: Theory, Methods & Applications 2010,72(5):2259–2261. 10.1016/j.na.2009.10.026
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Chen G, Huang X, Yang X: Vector Optimization, Lecture Notes in Economics and Mathematical Systems. Volume 541. Springer, Berlin, Germany; 2005:x+306.
Du W-S: On some nonlinear problems induced by an abstract maximal element principle. Journal of Mathematical Analysis and Applications 2008,347(2):391–399. 10.1016/j.jmaa.2008.06.020
Du W-S: Some new results and generalizations in metric fixed point theory. Nonlinear Analysis: Theory, Methods & Applications 2010, 73: 1439–1446. 10.1016/j.na.2010.05.007
Taylor AE, Lay DC: Introduction to Functional Analysis. 2nd edition. John Wiley & Sons, New York, NY, USA; 1980:xi+467.
Acknowledgment
This research was supported by the National Science Council of the Republic of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Du, WS. Nonlinear Contractive Conditions for Coupled Cone Fixed Point Theorems. Fixed Point Theory Appl 2010, 190606 (2010). https://doi.org/10.1155/2010/190606
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/190606
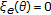 .
.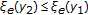
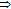
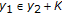 ) does not hold in general. For example, let
) does not hold in general. For example, let  , and
, and 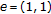 . Then
. Then 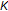 is a proper, closed, convex, and pointed cone in
is a proper, closed, convex, and pointed cone in  with
with  and
and  . For
. For 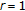 , it is easy to see that
, it is easy to see that 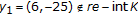 , and
, and 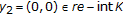 . By applying (iii) and (iv) of Theorem 2.1, we have
. By applying (iii) and (iv) of Theorem 2.1, we have 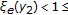
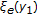 but indeed
but indeed 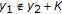 .
.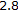 ] and some results in [
] and some results in [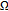 of
of 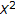 , such that
, such that 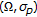 is a complete metric space.
is a complete metric space. ].
].