- Research Article
- Open access
- Published:
Existence of Solutions and Algorithm for a System of Variational Inequalities
Fixed Point Theory and Applications volume 2010, Article number: 182539 (2010)
Abstract
We obtain some existence results for a system of variational inequalities (for short, denoted by SVI) by Brouwer fixed point theorem. We also establish the existence and uniqueness theorem using the projection technique for the SVI and suggest an iterative algorithm and analysis convergence of the algorithm.
1. Questions under Consideration in This Paper
Suppose that  is a nonempty closed and convex subset of
is a nonempty closed and convex subset of  ;
;  is a vector-valued mapping. Variational inequality problem (for short, VI
is a vector-valued mapping. Variational inequality problem (for short, VI ) is to find an
) is to find an  , such that
, such that

We denote the solution set for VI by
by  . In this paper, we suggest and study the following SVI: find
. In this paper, we suggest and study the following SVI: find  , such that
, such that

where  ,
,  are vector-valued mappings, and
are vector-valued mappings, and 
 The above SVI can be described as
The above SVI can be described as

2. Existence and Uniqueness of Solutions for SVI
In this paper, otherwise specification,  is a n-dimensional Euclidean space, for all
is a n-dimensional Euclidean space, for all  ,
,  denotes the inner product between
denotes the inner product between  and
and  ,
,  denotes norm of
denotes norm of  , that is,
, that is,  .
.
In order to obtain our main results, we recall the following definitions and lemmas.
Definition 2.1.
Let  be a nonempty subset, and let
be a nonempty subset, and let  be a vector-valued mapping.
be a vector-valued mapping.
(i) is said to be monotone if, for all
is said to be monotone if, for all  ,
, 
(ii) is said to be strictly monotone if, for all
is said to be strictly monotone if, for all  ,
,  ,
, 
(iii) is said to be strongly monotone if there exists a constant
is said to be strongly monotone if there exists a constant  such that
such that

(iv) is said to be coercive if there exists an
is said to be coercive if there exists an  and a constant
and a constant  such that
such that  and
and

(v) is said to be Lipschitz continuous if there exists a constant
is said to be Lipschitz continuous if there exists a constant  such that
such that

Remark 2.2.
It is easy to see that

Based on the above all kinds of monotonicity, we have the following existence results for  .
.
Lemma 2.3 (see [1]).
Let  be nonempty compact and convex set, and let
be nonempty compact and convex set, and let  be continuous mapping. Then
be continuous mapping. Then  must has solution.
must has solution.
Lemma 2.4 (see [2]).
Let  be nonempty closed and convex set, and let
be nonempty closed and convex set, and let  be continuous mapping.
be continuous mapping.
(i)If  is strictly monotone, then
is strictly monotone, then  has at most one solution,
has at most one solution,
(ii)If  is coercive, then
is coercive, then  must has solution,
must has solution,
(iii)If  is strongly monotone, then
is strongly monotone, then  has a unique solution.
has a unique solution.
In order to obtain the existence results for SVI, one needs to study parametric variational inequalities  and
and  in SVI.
in SVI.
Setting  and
and  is the feasible region of SVI,
is the feasible region of SVI,  ,
,  are nonempty subset, and
are nonempty subset, and  ,
,  are two continuous mappings. At first, one considers
are two continuous mappings. At first, one considers  , which is a parametric variational inequality with respect to
, which is a parametric variational inequality with respect to  in SVI.
in SVI.
Theorem 2.5.
In  , assume that
, assume that  and
and  are two compact and convex sets,
are two compact and convex sets,  is continuous, and
is continuous, and  is strictly monotone in
is strictly monotone in  . Then, for any given
. Then, for any given  ,
,  has a unique solution and for all
has a unique solution and for all  , there exists an implicit function
, there exists an implicit function  which is the unique solution to
which is the unique solution to  . In addition, the implicit function
. In addition, the implicit function  determined by
determined by  is continuous on
is continuous on  .
.
Proof.
-
(i)
For any given
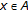 , since
, since 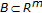 is compact and convex and
is compact and convex and  is continuous on
is continuous on 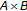 , then by Lemma 2.3, parametric variational inequality
, then by Lemma 2.3, parametric variational inequality 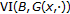 has solutions. In terms of strict monotonicity of the mapping
has solutions. In terms of strict monotonicity of the mapping 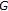 in
in 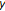 and Lemma 2.4, we know that
and Lemma 2.4, we know that  has a unique solution. So, for all
has a unique solution. So, for all 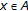 , the implicit function
, the implicit function 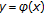 determined by
determined by 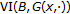 is well defined.
is well defined. -
(ii)
We claim that
 is continuous on
is continuous on  . In fact, for any given
. In fact, for any given 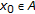 ,
, 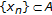 ,
, 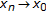 as
as  , by (i), we know that for all
, by (i), we know that for all  , there exists
, there exists 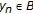 , such that
, such that  . That is,
. That is,

Since  is bounded, then there exists convergent subsequence
is bounded, then there exists convergent subsequence  such that
such that  as
as  , and
, and  . In the following, we prove that
. In the following, we prove that  is a solution to
is a solution to  in
in  . For given
. For given  , there exists sequence
, there exists sequence  such that
such that  and
and  as
as  in view of the closedness of
in view of the closedness of  . Letting
. Letting  in (2.5), we have
in (2.5), we have

that is,

observe that  is continuous, and letting
is continuous, and letting  in (2.7), we have
in (2.7), we have

For  is arbitrary, then
is arbitrary, then  is a solution to
is a solution to  , implying
, implying  . In order to explain that
. In order to explain that  is continuous at
is continuous at  , we only need to know that the sequence
, we only need to know that the sequence  satisfies
satisfies  as
as  . Let
. Let  be any subsequence of
be any subsequence of  . Since
. Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  such that
such that  as
as  . Using the method appeared in Theorem 2.5, we can show that
. Using the method appeared in Theorem 2.5, we can show that

Thus, by the uniqueness of the solution to the problem  , we conclude that
, we conclude that  . Since,
. Since,  is arbitrary, we can conclude that
is arbitrary, we can conclude that  as
as  , which means that implicit function
, which means that implicit function  is continuous at
is continuous at  . For
. For  is arbitrary, we know that
is arbitrary, we know that  is continuous on
is continuous on  .
.
From Theorem 2.5, we see that in order to ensure that  is well defined, the condition that
is well defined, the condition that  is strictly monotone on
is strictly monotone on  is necessary, but the boundedness of
is necessary, but the boundedness of  is a strong condition. As usual,
is a strong condition. As usual,  is unbounded (e.g., inequality constraint set
is unbounded (e.g., inequality constraint set  , where
, where  , is always unbounded). So, we try to weaken the boundedness of
, is always unbounded). So, we try to weaken the boundedness of  . For this, we introduce the concept uniform coercivity of
. For this, we introduce the concept uniform coercivity of  in
in  .
.
Definition 2.6.
In  , let
, let  ;
;  is said to be uniformly coercive near
is said to be uniformly coercive near  , if there exists some neighbourhood
, if there exists some neighbourhood  of
of  ,
,  and
and  such that
such that  and for all
and for all  ,
,

where  and
and  .
.
If for each  ,
,  is uniformly coercive near
is uniformly coercive near  , then
, then  is said to be uniformly coercive on
is said to be uniformly coercive on  .
.
Lemma 2.7.
In  , let
, let  be nonempty closed and convex set, and let
be nonempty closed and convex set, and let  be uniformly coercive near
be uniformly coercive near  , then there exists some neighbourhood
, then there exists some neighbourhood  of
of  , such that
, such that  is bounded set.
is bounded set.
Proof.
For given  , by the definition of the uniform coercivity of
, by the definition of the uniform coercivity of  near
near  , there exists some neighbourhood
, there exists some neighbourhood  of
of  ,
,  and
and  such that
such that  and for all
and for all  ,
,

Let  It is obvious that
It is obvious that  is a nonempty bounded closed convex subset of
is a nonempty bounded closed convex subset of  In view of Lemma 2.3, we know that
In view of Lemma 2.3, we know that  must have solution. That is, there exists an
must have solution. That is, there exists an  such that
such that

Now, we state that  and
and  In fact, if
In fact, if  , for all
, for all  , join
, join  and
and  into
into  with
with  . Then take small enough
. Then take small enough  such that
such that  . Substituting
. Substituting  with
with  in (2.12), we have
in (2.12), we have

implying that  and
and  . On the other hand, if
. On the other hand, if  , substituting
, substituting  with
with  in (2.11), we have
in (2.11), we have

which, by plus (2.12), we get

For all  ,
,  , consider the connection of
, consider the connection of  and
and  ; following the same argument, we have that
; following the same argument, we have that  and
and  Therefore,
Therefore,  and
and  . That is,
. That is,  is bounded. For
is bounded. For  is arbitrary, the conclusion holds. This completes the proof.
is arbitrary, the conclusion holds. This completes the proof.
If the boundedness of  is replaced by the uniform coercivity of
is replaced by the uniform coercivity of  in Theorem 2.5, then we have the following result.
in Theorem 2.5, then we have the following result.
Theorem 2.8.
In  , let
, let  be nonempty closed and convex set, and let
be nonempty closed and convex set, and let  be uniformly coercive on
be uniformly coercive on  with respect to
with respect to  and strict monotone in
and strict monotone in  . Then for each
. Then for each  ,
,  has a unique solution, and for all
has a unique solution, and for all  , the implicit function
, the implicit function  determined by
determined by  is continuous on
is continuous on  .
.
Proof.
-
(i)
For given
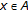 , by Lemma 2.4 and the coercivity of
, by Lemma 2.4 and the coercivity of  on
on  , we know that
, we know that 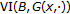 has solution. Noting that
has solution. Noting that 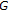 is strictly monotone in
is strictly monotone in 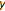 ,
, 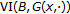 has a unique solution, and so the implicit function
has a unique solution, and so the implicit function 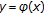 is well defined.
is well defined. -
(ii)
For given
 ,
, 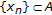 , satisfying
, satisfying 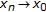 as
as 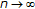 . By Lemma 2.7, there exists some neighbourhood
. By Lemma 2.7, there exists some neighbourhood  of
of 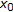 and bounded open set
and bounded open set  , such that
, such that 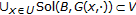 , that is, the solution set of
, that is, the solution set of 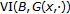 denoted by
denoted by  .
. 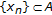 such that
such that  as
as 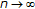 . Let
. Let  without generality, then
without generality, then  is bounded; the following argument is similar to Theorem 2.5, so it is omitted, and this completes the proof.
is bounded; the following argument is similar to Theorem 2.5, so it is omitted, and this completes the proof.
Set  ; it is to see that
; it is to see that  . We will investigate the parametric variational inequality
. We will investigate the parametric variational inequality  with respect to
with respect to  in SVI.
in SVI.
Corollary 2.9.
In  , let
, let  be two nonempty compact and convex subsets,
be two nonempty compact and convex subsets,  be continuous and strict monotone in
be continuous and strict monotone in  . Then for each given
. Then for each given  ,
,  has a unique solution, and for all
has a unique solution, and for all  , the implicit function
, the implicit function  determined by
determined by  is continuous on
is continuous on  .
.
Proof.
The conclusion holds directly from Theorem 2.5.
Lemma 2.10 (see [3, (Brouwer fixed point theorem)]).
Let  be nonempty compact and convex set, and let
be nonempty compact and convex set, and let  be continuous. Then there exists an
be continuous. Then there exists an  , such that
, such that  .
.
Theorem 2.11.
In SVI, let  be two compact and convex subset, and let
be two compact and convex subset, and let  and
and  be two continuous mappings and strict monotone in
be two continuous mappings and strict monotone in  and
and  , respectively. Then SVI has solution.
, respectively. Then SVI has solution.
Proof.
By the given conditions of Theorems 2.11 and 2.5, we know that there exists continuous implicit function  determined by parametric variational inequality
determined by parametric variational inequality  with respect to
with respect to  in SVI. Also denoted the range of
in SVI. Also denoted the range of  by
by  . By Corollary 2.9, there exists continuous implicit function
. By Corollary 2.9, there exists continuous implicit function  determined by parametric variational inequality
determined by parametric variational inequality  with respect to
with respect to  in SVI such that for all
in SVI such that for all  ,
,  is the unique solution to
is the unique solution to  . Let
. Let  for all
for all  Making use of Brouwer fixed point theorem (Lemma 2.10), we have that there exists
Making use of Brouwer fixed point theorem (Lemma 2.10), we have that there exists  , such that
, such that  . Setting
. Setting  , by the definitions of
, by the definitions of  and
and  , we know that
, we know that  is a solution of SVI.
is a solution of SVI.
Corollary 2.12.
In SVI, let  be nonempty compact and convex subset, let
be nonempty compact and convex subset, let  be nonempty closed and convex subset, let
be nonempty closed and convex subset, let  and
and  be two continuous mappings, and
be two continuous mappings, and  be strict monotone in
be strict monotone in  and
and  , respectively. Let
, respectively. Let  be uniformly coercive on
be uniformly coercive on  with respect to
with respect to  . Then SVI has solution.
. Then SVI has solution.
Proof.
By Theorem 2.8 and similar argument in Theorem 2.11, our conclusion holds.
Now, we give the definition of uniformly strong monotonicity, which is stronger condition than the uniformly coercivity.
Definition 2.13.
Let  be vector-valued mapping; if there exists
be vector-valued mapping; if there exists  , such that for all
, such that for all  ,
,

then  is said to be uniformly strongly monotone in
is said to be uniformly strongly monotone in  .
.
Lemma 2.14.
In  , let
, let  be uniformly strongly monotone, then
be uniformly strongly monotone, then  is uniformly coercive.
is uniformly coercive.
Proof.
For given  , we only need to prove that
, we only need to prove that  is uniformly coercive at
is uniformly coercive at  . Let us consider
. Let us consider  . Assume that
. Assume that  is a solution to
is a solution to  , and
, and  ,
,  . Since
. Since  is strongly monotone, then there exists
is strongly monotone, then there exists  , such that for all
, such that for all  ,
,

Letting  in (2.17), we have
in (2.17), we have

Noting that  is a solution to
is a solution to  , we have
, we have

Combining (2.18), we obtain

Since  is continuous, then there exists some neighbourhood
is continuous, then there exists some neighbourhood  of
of  , such that for all
, such that for all  ,
,

which implies that  is uniform coercive at
is uniform coercive at  .
.
Using the uniformly strong monotonicity of  , we can obtain the following existence result for SVI under the condition that
, we can obtain the following existence result for SVI under the condition that  is a nonempty closed and convex subset of
is a nonempty closed and convex subset of  .
.
Corollary 2.15.
In SVI, let  be a nonempty closed and convex set, let
be a nonempty closed and convex set, let  be a compact and convex set, let
be a compact and convex set, let  be two continuous mapping, let
be two continuous mapping, let  be uniformly strongly monotone in
be uniformly strongly monotone in  , and let
, and let  be strictly monotone in
be strictly monotone in  . Then SVI has solution.
. Then SVI has solution.
Proof.
By Lemma 2.14 and Corollary 2.12, it is easy to see that the conclusion holds.
Corollary 2.16.
In SVI, Let  and
and  be nonempty closed and convex subsets, let
be nonempty closed and convex subsets, let  be two continuous mappings, and let
be two continuous mappings, and let  be uniformly strongly monotone in
be uniformly strongly monotone in  , and let
, and let  be uniformly coercive and strict monotone in
be uniformly coercive and strict monotone in  . Then SVI has solution.
. Then SVI has solution.
Furthermore, If  and
and  are Lipschitz continuous in
are Lipschitz continuous in  and
and  , respectively, one can obtain the following existence and uniqueness result for SVI.
, respectively, one can obtain the following existence and uniqueness result for SVI.
Theorem 2.17.
In SVI, let  be nonempty compact and convex subsets, let
be nonempty compact and convex subsets, let  be uniformly strongly monotone with constant
be uniformly strongly monotone with constant  and Lipschitz continuous with Lipschitz constant
and Lipschitz continuous with Lipschitz constant  in
in  , and Lipschitz continuous with constant
, and Lipschitz continuous with constant  in
in  , and let
, and let  be uniformly strongly monotone with constant
be uniformly strongly monotone with constant  and Lipschitz continuous with constant
and Lipschitz continuous with constant  in
in  , and Lipschitz continuous with constant
, and Lipschitz continuous with constant  in
in  . If there exists constants
. If there exists constants  such that
such that

then SVI has a unique solution.
In order to prove Theorem 2.17, we need the following lemma.
Lemma 2.18 (see [4]).
In SVI, let  be nonempty closed and convex subsets, and let
be nonempty closed and convex subsets, and let  be two continuous mappings. SVI has solution
be two continuous mappings. SVI has solution  if and only if
if and only if  satisfies
satisfies

where  denote the projection from
denote the projection from  and
and  to
to  and
and  , respectively; furthermore, projection operator is nonexpansive and
, respectively; furthermore, projection operator is nonexpansive and  are constants.
are constants.
The Proof of Theorem 2.17
For arbitrary given constant  , define
, define  and
and  by
by

For any  , it follows from (2.24) and Lemma 2.18 that
, it follows from (2.24) and Lemma 2.18 that

We have used the strong monotonicity and Lipschitz continuity of  in
in  and Lipschitz continuity of
and Lipschitz continuity of  in
in  . Similarly, we have
. Similarly, we have

It follows from (2.25) and (2.26) that

where

Define  on
on  by
by

It is easy to see that  is a Banach space. For any given
is a Banach space. For any given  , define
, define  by
by

By assumption, we know that  . It follows from (2.27) that
. It follows from (2.27) that

which implies that  is a contraction operator. Hence, there exists a unique
is a contraction operator. Hence, there exists a unique  , such that
, such that

That is,

By Lemma 2.18,  is the unique solution of SVI.
is the unique solution of SVI.
3. Iterative Algorithm and Convergence
In this section, we will construct an iterative algorithm for approximating the unique solution of SVI and discuss the convergence analysis of the algorithm.
Lemma 3.1 (see, [5]).
Let  and
and  be two real sequence of nonnegative numbers that satisfy the following conditions.
be two real sequence of nonnegative numbers that satisfy the following conditions.
(i) and
and  ,
,
(ii)
Then,  converges to 0 as
converges to 0 as  .
.
Algorithm 3.2.
Let  and
and  be the same as in Theorem 2.17. For any given
be the same as in Theorem 2.17. For any given  , define iterative sequence
, define iterative sequence  by
by

where

Theorem 3.3.
Let  and
and  be the same as in Theorem 2.17. Assume that all the conditions of Theorem 2.17 hold. Then,
be the same as in Theorem 2.17. Assume that all the conditions of Theorem 2.17 hold. Then,  generated by Algorithm 3.2 converges to the unique solution
generated by Algorithm 3.2 converges to the unique solution  of SVI and there exists
of SVI and there exists  , such that
, such that

Proof.
By Theorem 2.17, SVI admits a unique solution  . It follows from Lemma 2.18 that
. It follows from Lemma 2.18 that

It follows from (3.1) and (3.4) that

By (3.5), we get

where  is defined by
is defined by

Set

Then (3.6) can be rewritten as

By (3.2), we know that  . It follows from Lemma 3.1 that
. It follows from Lemma 3.1 that  and that
and that

for all  . Therefore,
. Therefore,  converges geometrically to the unique solution
converges geometrically to the unique solution  of SVI. This completes the proof.
of SVI. This completes the proof.
References
Mosco U: Introduction to Approximation Solution of Variational Inequalities. Shanghai Science and Technology, Shanghai, China; 1985.
Outrata J, Kočvara M, Zowe J: Nonsmooth Approach to Optimization Problems with Equilibrium Constraints, Nonconvex Optimization and Its Applications. Volume 28. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1998:xxii+273.
Smart DR: Fixed Point Theorems. Cambridge University Press, Cambridge, UK; 1980.
Xiu NH, Zhang JZ: Local convergence analysis of projection-type algorithms: unified approach. Journal of Optimization Theory and Applications 2002,115(1):211–230. 10.1023/A:1019637315803
Fang Y-P, Huang N-J, Thompson HB: A new system of variational inclusions with -monotone operators in Hilbert spaces. Computers & Mathematics with Applications 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037
Acknowledgment
The authors are grateful to the referee for his/her valuable suggestions and comments that help to present the paper in the present form. This work was supported by the Doctoral Initiating Foundation of Liaoning Province (20071097).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhao, Y., Xia, Z., Pang, L. et al. Existence of Solutions and Algorithm for a System of Variational Inequalities. Fixed Point Theory Appl 2010, 182539 (2010). https://doi.org/10.1155/2010/182539
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/182539
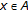 , since
, since 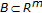 is compact and convex and
is compact and convex and  is continuous on
is continuous on 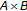 , then by Lemma 2.3, parametric variational inequality
, then by Lemma 2.3, parametric variational inequality 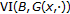 has solutions. In terms of strict monotonicity of the mapping
has solutions. In terms of strict monotonicity of the mapping 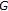 in
in 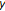 and Lemma 2.4, we know that
and Lemma 2.4, we know that  has a unique solution. So, for all
has a unique solution. So, for all 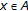 , the implicit function
, the implicit function 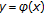 determined by
determined by 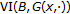 is well defined.
is well defined. is continuous on
is continuous on  . In fact, for any given
. In fact, for any given 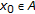 ,
, 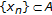 ,
, 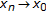 as
as  , by (i), we know that for all
, by (i), we know that for all  , there exists
, there exists 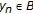 , such that
, such that  . That is,
. That is,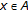 , by Lemma 2.4 and the coercivity of
, by Lemma 2.4 and the coercivity of  on
on  , we know that
, we know that 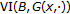 has solution. Noting that
has solution. Noting that 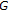 is strictly monotone in
is strictly monotone in 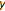 ,
, 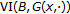 has a unique solution, and so the implicit function
has a unique solution, and so the implicit function 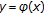 is well defined.
is well defined. ,
, 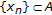 , satisfying
, satisfying 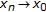 as
as 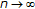 . By Lemma 2.7, there exists some neighbourhood
. By Lemma 2.7, there exists some neighbourhood  of
of 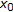 and bounded open set
and bounded open set  , such that
, such that 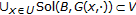 , that is, the solution set of
, that is, the solution set of 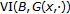 denoted by
denoted by  .
. 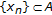 such that
such that  as
as 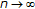 . Let
. Let  without generality, then
without generality, then  is bounded; the following argument is similar to Theorem 2.5, so it is omitted, and this completes the proof.
is bounded; the following argument is similar to Theorem 2.5, so it is omitted, and this completes the proof.