- Research Article
- Open access
- Published:
Modified Hybrid Algorithm for a Family of Quasi- -Asymptotically Nonexpansive Mappings
-Asymptotically Nonexpansive Mappings
Fixed Point Theory and Applications volume 2010, Article number: 170701 (2010)
Abstract
The purpose of this paper is to propose a modified hybrid projection algorithm and prove strong convergence theorems for a family of quasi- -asymptotically nonexpansive mappings. The method of the proof is different from the original one. Our results improve and extend the corresponding results announced by Zhou et al. (2010), Kimura and Takahashi (2009), and some others.
-asymptotically nonexpansive mappings. The method of the proof is different from the original one. Our results improve and extend the corresponding results announced by Zhou et al. (2010), Kimura and Takahashi (2009), and some others.
1. Introduction
Let  be a real Banach space and
be a real Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . A mapping
. A mapping  is said to be asymptotically nonexpansive [1] if there exists a sequence
is said to be asymptotically nonexpansive [1] if there exists a sequence  of positive real numbers with
of positive real numbers with  such that
such that

for all  and all
and all  .
.
The class of asymptotically nonexpansive mappings was introduced by Goebel and Kirk [1] in 1972. They proved that if  is a nonempty bounded closed convex subset of a uniformly convex Banach space
is a nonempty bounded closed convex subset of a uniformly convex Banach space  , then every asymptotically nonexpansive self-mapping
, then every asymptotically nonexpansive self-mapping  of
of  has a fixed point. Further, the set
has a fixed point. Further, the set  of fixed points of
of fixed points of  is closed and convex. Since 1972, a host of authors have studied the weak and strong convergence problems of the iterative algorithms for such a class of mappings (see, e.g., [1–3] and the references therein).
is closed and convex. Since 1972, a host of authors have studied the weak and strong convergence problems of the iterative algorithms for such a class of mappings (see, e.g., [1–3] and the references therein).
It is well known that in an infinite-dimensional Hilbert space, the normal Mann's iterative algorithm has only weak convergence, in general, even for nonexpansive mappings. Consequently, in order to obtain strong convergence, one has to modify the normal Mann's iteration algorithm; the so-called hybrid projection iteration method is such a modification.
The hybrid projection iteration algorithm (HPIA) was introduced initially by Haugazeau [4] in 1968. For 40 years, (HPIA) has received rapid developments. For details, the readers are referred to papers in [5–11] and the references therein.
In 2003, Nakajo and Takahashi [6] proposed the following modification of the Mann iteration method for a nonexpansive mapping  in a Hilbert space
in a Hilbert space  :
:

where  is a closed convex subset of
is a closed convex subset of  ,
,  denotes the metric projection from
denotes the metric projection from  onto a closed convex subset
onto a closed convex subset  of
of  . They proved that if the sequence
. They proved that if the sequence  is bounded above from one then the sequence
is bounded above from one then the sequence  generated by (1.2) converges strongly to
generated by (1.2) converges strongly to  , where
, where  denote the fixed points set of
denote the fixed points set of  .
.
In 2006, Kim and Xu [12] proposed the following modification of the Mann iteration method for asymptotically nonexpansive mapping  in a Hilbert space
in a Hilbert space  :
:

where  is bounded closed convex subset and
is bounded closed convex subset and

They proved that if the sequence  is bounded above from one, then the sequence
is bounded above from one, then the sequence  generated by (1.3) converges strongly to
generated by (1.3) converges strongly to  .
.
They also proposed the following modification of the Mann iteration method for asymptotically nonexpansive semigroup  in a Hilbert space
in a Hilbert space  :
:

where  is bounded closed convex subset and
is bounded closed convex subset and

and  is nonincreasing in
is nonincreasing in  and bounded measurable function such that,
and bounded measurable function such that,  for all
for all  as
as  , and for each
, and for each  ,
,

They proved that if the sequence  is bounded above from one, then the sequence
is bounded above from one, then the sequence  generated by (1.5) converges strongly to
generated by (1.5) converges strongly to  , where
, where  denote the common fixed points set of
denote the common fixed points set of  .
.
In 2006, Martinez-Yanes and Xu [7] proposed the following modification of the Ishikawa iteration method for nonexpansive mapping  in a Hilbert space
in a Hilbert space  :
:

where  is a closed convex subset of
is a closed convex subset of  . They proved that if the sequence
. They proved that if the sequence  is bounded above from one and
is bounded above from one and  , then the sequence
, then the sequence  generated by (1.8) converges strongly to
generated by (1.8) converges strongly to  .
.
Martinez-Yanes and Xu [7] proposed also the following modification of the Halpern iteration method for nonexpansive mapping  in a Hilbert space
in a Hilbert space  :
:

where  is a closed convex subset of
is a closed convex subset of  . They proved that if the sequence
. They proved that if the sequence  , then the sequence
, then the sequence  generated by (1.9) converges strongly to
generated by (1.9) converges strongly to  .
.
In 2005, Matsushita and Takahashi [8] proposed the following hybrid iteration method with generalized projection for relatively nonexpansive mapping  in a Banach space
in a Banach space  :
:

They proved the following convergence theorem.
Theorem MT..
Let  be a uniformly convex and uniformly smooth Banach space, let
be a uniformly convex and uniformly smooth Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , let
, let  be a relatively nonexpansive mapping from
be a relatively nonexpansive mapping from  into itself, and let
into itself, and let  be a sequence of real numbers such that
be a sequence of real numbers such that  and
and  . Suppose that
. Suppose that  is given by (1.10), where
is given by (1.10), where  is the duality mapping on
is the duality mapping on  . If
. If  is nonempty, then
is nonempty, then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
In 2009, Zhou et al. [11] proposed the following modification of the hybrid iteration method with generalized projection for a family of closed and quasi- -asymptotically nonexpansive mappings
-asymptotically nonexpansive mappings  in a Banach space
in a Banach space  :
:

They proved the following convergence theorem.
Theorem ZGT.
Let
 be a nonempty bounded closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty bounded closed convex subset of a uniformly convex and uniformly smooth Banach space
 , and let
, and let
 be a family of
be a family of
 -asymptotically nonexpansive mappings such that
-asymptotically nonexpansive mappings such that
 . Assume that every
. Assume that every
 ,
,
 is asymptotically regular on
is asymptotically regular on
 . Let
. Let
 be a real sequence in
be a real sequence in
 such that
such that
 . Define a sequence
. Define a sequence
 as given by ( 1 ), then
as given by ( 1 ), then
 converges strongly to
converges strongly to
 , where
, where
 ,
,
 for all
for all
 ,
,
 , and
, and
 is the generalized projection from
is the generalized projection from
 onto
onto
 .
.
Very recently, Kimura and Takahashi [13] established strong convergence theorems by the hybrid method for a family of relatively nonexpansive mappings as follows.
Theorem KT.
Let
 be a strictly convex reflexive Banach space having the Kadec-Klee property and a Fréchet differentiable norm, and let
be a strictly convex reflexive Banach space having the Kadec-Klee property and a Fréchet differentiable norm, and let
 be a nonempty and closed convex subset of
be a nonempty and closed convex subset of
 and
and
 a family of relatively nonexpensive mappings of
a family of relatively nonexpensive mappings of
 into itself having a common fixed point. Let
into itself having a common fixed point. Let
 be a sequence in
be a sequence in
 such that
such that
 . For an arbitrarily chosen point
. For an arbitrarily chosen point
 , generate a sequence
, generate a sequence
 by the following iterative scheme:
by the following iterative scheme:
 , and
, and

for every  , then
, then  converges strongly to
converges strongly to  , where
, where  is the set of common fixed points of
is the set of common fixed points of  and
and  is the metric projection of
is the metric projection of  onto a nonempty closed convex subset
onto a nonempty closed convex subset  of
of  .
.
Motivated by these results above, the purpose of this paper is to propose a Modified hybrid projection algorithm and prove strong convergence theorems for a family of  -
- -asymptotically nonexpansive mappings which are asymptotically regular on
-asymptotically nonexpansive mappings which are asymptotically regular on  . In order to get the strong convergence theorems for such a family of mappings, the classical hybrid projection iteration algorithm is modified and then is used to approximate the common fixed points of such a family of mappings. In the meantime, the method of the proof is different from the original one. Our results improve and extend the corresponding results announced by Zhou et al. [11], and Kimura and Takahashi [13], and some others.
. In order to get the strong convergence theorems for such a family of mappings, the classical hybrid projection iteration algorithm is modified and then is used to approximate the common fixed points of such a family of mappings. In the meantime, the method of the proof is different from the original one. Our results improve and extend the corresponding results announced by Zhou et al. [11], and Kimura and Takahashi [13], and some others.
2. Preliminaries
Let  be a Banach space with dual
be a Banach space with dual  . Denote by
. Denote by  the duality product. The normalize duality mapping
the duality product. The normalize duality mapping  from
from  to
to  is defined by
is defined by

for all  , where
, where  denotes the dual space of
denotes the dual space of  and
and  the generalized duality pairing between
the generalized duality pairing between  and
and  . It is well known that if
. It is well known that if  is uniformly convex, then
is uniformly convex, then  is uniformly continuous on bounded subsets of
is uniformly continuous on bounded subsets of  .
.
It is also very well known that if  is a nonempty closed convex subset of a Hilbert space
is a nonempty closed convex subset of a Hilbert space  and
and  is the metric projection of
is the metric projection of  onto
onto  , then
, then  is nonexpansive. This fact actually characterizes Hilbert spaces
is nonexpansive. This fact actually characterizes Hilbert spaces  , and consequently, it is not available in more general Banach spaces. In this connection, Alber [14] recently introduced a generalized projection operator
, and consequently, it is not available in more general Banach spaces. In this connection, Alber [14] recently introduced a generalized projection operator  in a Banach space
in a Banach space  which is an analogue of the metric projection in Hilbert spaces.
which is an analogue of the metric projection in Hilbert spaces.
Next, we assume that  is a real smooth Banach space. Let us consider the functional defined by [7, 8] as
is a real smooth Banach space. Let us consider the functional defined by [7, 8] as

for all  . Observe that, in a Hilbert space
. Observe that, in a Hilbert space  , (2.2) reduces to
, (2.2) reduces to  ,
,  ,
, .
.
The generalized projection  is a map that assigns to an arbitrary point
is a map that assigns to an arbitrary point  , the minimum point of the functional
, the minimum point of the functional  , that is,
, that is,  , where
, where  is the solution to the minimization problem
is the solution to the minimization problem

Existence and uniqueness of the operator  follow from the properties of the C functional
follow from the properties of the C functional  and strict monotonicity of the mapping
and strict monotonicity of the mapping  (see, e.g., [14–18]). In Hilbert spaces,
(see, e.g., [14–18]). In Hilbert spaces,  . It is obvious from the definition of function
. It is obvious from the definition of function  that
that

for all  .
.
Remark 2.1.
If  is a reflexive strictly convex and smooth Banach space, then for
is a reflexive strictly convex and smooth Banach space, then for  ,
,  if and only if
if and only if  . It is sufficient to show that if
. It is sufficient to show that if  , then
, then  . From (2.4), we have
. From (2.4), we have  . This implies that
. This implies that  From the definitions of
From the definitions of  , we have
, we have  . That is,
. That is,  see [17, 18] for more details.
see [17, 18] for more details.
Let  be a closed convex subset of
be a closed convex subset of  and
and  a mapping from
a mapping from  into itself.
into itself.  is said to be
is said to be  -asymptotically nonexpansive if there exists some real sequence
-asymptotically nonexpansive if there exists some real sequence  with
with  and
and  such that
such that  for all
for all  and
and  .
.  is said to be
is said to be  -asymptotically nonexpansive [9] if there exists some real sequence
-asymptotically nonexpansive [9] if there exists some real sequence  with
with  and
and  and
and  such that
such that  for all
for all  ,
,  , and
, and  .
.  is said to be asymptotically regular on
is said to be asymptotically regular on  if, for any bounded subset
if, for any bounded subset  of
of  , there holds the following equality:
, there holds the following equality:

We remark that a  -asymptotically nonexpansive mapping with a nonempty fixed point set
-asymptotically nonexpansive mapping with a nonempty fixed point set  is a quasi-
is a quasi- -asymptotically nonexpansive mapping, but the converse may be not true.
-asymptotically nonexpansive mapping, but the converse may be not true.
We present some examples which are closed and quasi- -asymptotically nonexpansive.
-asymptotically nonexpansive.
Example 2.2.
Let  be a real line. We define a mapping
be a real line. We define a mapping  by
by

Then  is continuous quasi-nonexpansive, and hence it is closed and
is continuous quasi-nonexpansive, and hence it is closed and  nonexpansive with the constant sequence
nonexpansive with the constant sequence  but not asymptotically nonexpansive.
but not asymptotically nonexpansive.
Example 2.3.
Let  be a uniformly smooth and strictly convex Banach space, and
be a uniformly smooth and strictly convex Banach space, and  is a maximal monotone mapping such that
is a maximal monotone mapping such that  is nonempty. Then,
is nonempty. Then,  is a closed and quasi-
is a closed and quasi- -asymptotically nonexpansive mapping from
-asymptotically nonexpansive mapping from  onto
onto  , and
, and  .
.
Example 2.4.
Let  be the generalized projection from a smooth, strictly convex, and reflexive Banach space
be the generalized projection from a smooth, strictly convex, and reflexive Banach space  onto a nonempty closed convex subset
onto a nonempty closed convex subset  of
of  . Then,
. Then,  is a closed and quasi-
is a closed and quasi- -asymptotically nonexpansive mapping from
-asymptotically nonexpansive mapping from  onto
onto  with
with  .
.
Let  be a sequence of nonempty closed convex subsets of a reflexive Banach space
be a sequence of nonempty closed convex subsets of a reflexive Banach space  . We denote two subsets
. We denote two subsets  and
and  as follows:
as follows:  if and only if there exists
if and only if there exists  such that
such that  converges strongly to
converges strongly to  and that
and that  for all
for all  . Similarly,
. Similarly,  if and only if there exists a subsequence
if and only if there exists a subsequence  of
of  and a sequence
and a sequence  such that
such that  converges weakly to
converges weakly to  and that
and that  for all
for all  . We define the Mosco convergence [19] of
. We define the Mosco convergence [19] of  as follows. If
as follows. If  satisfies that
satisfies that  , it is said that
, it is said that  converges to
converges to  in the sense of Mosco, and we write
in the sense of Mosco, and we write  . For more details, see [20].
. For more details, see [20].
The following theorem plays an important role in our results.
Theorem 2.5 (see Ibaraki et al. [21]).
Let  be a smooth, reflexive, and strictly convex Banach space having the Kadec-Klee property. Let
be a smooth, reflexive, and strictly convex Banach space having the Kadec-Klee property. Let  be a sequence of nonempty closed convex subsets of
be a sequence of nonempty closed convex subsets of  . If
. If  exists and is nonempty, then
exists and is nonempty, then  converges strongly to
converges strongly to  for each
for each  .
.
We also need the following lemmas for the proof of our main results.
Lemma 2.6 (Kamimura and Takahashi [16]).
Let  be a uniformly convex and smooth Banach space, and let
be a uniformly convex and smooth Banach space, and let  ,
,  be two sequences of
be two sequences of  if
if  and either
and either  or
or  is bounded, then
is bounded, then  .
.
Lemma 2.7 (Alber [14]).
Let  be a reflexive, strictly convex and smooth Banach space, let
be a reflexive, strictly convex and smooth Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  . Then
. Then

for all  .
.
Lemma 2.8.
Let  be a uniformly convex and smooth Banach space, let
be a uniformly convex and smooth Banach space, let  be a closed convex subset of
be a closed convex subset of  , and let
, and let  be a closed and
be a closed and  -asympotically nonexpansive mapping from
-asympotically nonexpansive mapping from  into itself. Then
into itself. Then  is a closed convex subset of
is a closed convex subset of  .
.
3. A Modified Algorithm and Strong Convergence Theorems
Now we are in a proposition to prove the main results of this paper. In the sequel, we use the letter  to denote an index set.
to denote an index set.
Theorem 3.1.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  , and let
, and let  be a family of closed and
be a family of closed and  -asymptotically nonexpansive mappings such that
-asymptotically nonexpansive mappings such that  . Assume that every
. Assume that every  ,
,  is asymptotically regular on
is asymptotically regular on  . Let
. Let  ,
,  ,
,  be real sequences in
be real sequences in  such that
such that  ,
,  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
Firstly, we show that  is closed and convex for each
is closed and convex for each  .
.
From the definition of  , it is obvious that
, it is obvious that  is closed for each
is closed for each  . We show that
. We show that  is convex for each
is convex for each  . Observe that the set
. Observe that the set

can be written as

For  and
and  , denote
, denote  ,
,  , and
, and  by noting that
by noting that  is convex, we have
is convex, we have

So we obtain

which infers that  , so we get that
, so we get that  is convex for each
is convex for each  . Thus
. Thus  is closed and convex for every
is closed and convex for every  .
.
Secondly, we prove that  , for all
, for all  .
.
Indeed, by noting that  is convex and using (2.2), we have, for any
is convex and using (2.2), we have, for any  and all
and all  , that
, that

which infers that  , for all
, for all  and
and  , and hence
, and hence  . This proves that
. This proves that  , for all
, for all  and
and  .
.
Thirdly, we will show that  .
.
Since  is a decreasing sequence of closed convex subsets of
is a decreasing sequence of closed convex subsets of  such that
such that  is nonempty, it follows that
is nonempty, it follows that

By Theorem 2.5,  converges strongly to
converges strongly to  .
.
Fourthly, we prove that  .
.
Since  , from the definition of
, from the definition of  , we get
, we get

From  , one obtains
, one obtains  as
as  , and it follows from
, and it follows from  , for every
, for every  that we have
that we have

and hence  as
as  by Lemma 2.6. It follows that
by Lemma 2.6. It follows that  as
as  . Since
. Since  is uniformly norm-to-norm continuous on any bounded sets of
is uniformly norm-to-norm continuous on any bounded sets of  , we conclude that
, we conclude that

for every  . By the definition of
. By the definition of  and the assumption on
and the assumption on  , we deduce that
, we deduce that

for every  and
and  . So we get
. So we get

Since  , we have
, we have  as
as  .
.
Since  is also uniformly norm-to-norm continuous on any bounded sets of
is also uniformly norm-to-norm continuous on any bounded sets of  , we conclude that
, we conclude that

Noting that  as
as  , we have
, we have

as  . Observe that
. Observe that

By using (3.14), (3.15), and the asymptotic regularity of  , we have
, we have

as  , that is,
, that is,  . Now the closedness property of
. Now the closedness property of  gives that
gives that  is a common fixed point of the family
is a common fixed point of the family  , thus
, thus  .
.
Finally, since  and
and  is a nonempty closed convex subset of
is a nonempty closed convex subset of  , we conclude that
, we conclude that  . This completes the proof.
. This completes the proof.
Remark 3.2.
The boundedness assumption on  in Theorem ZGT can be dropped.
in Theorem ZGT can be dropped.
Remark 3.3.
The asymptotic regularity assumption on  in Theorem 3.1 can be weakened to the assumption that
in Theorem 3.1 can be weakened to the assumption that  as
as  .
.
Recall that  is called uniformly Lipschitzian continuous if there exists some
is called uniformly Lipschitzian continuous if there exists some  such that
such that

for all  and
and  .
.
Remark 3.4.
The assumption that  as
as  can be replaced by the uniform Lipschitz continuity of
can be replaced by the uniform Lipschitz continuity of  .
.
With above observations, we have the following convergence result.
Corollary 3.5.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  , and let
, and let  be a family of uniformly Lipschitzian continuous and
be a family of uniformly Lipschitzian continuous and  -
-  -asymptotically nonexpansive mappings such that
-asymptotically nonexpansive mappings such that  . Let
. Let  ,
,  ,
,  be real sequences in
be real sequences in  such that
such that  ,
,  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
Following the proof lines of Theorem 3.1, we can prove that  is nonempty closed convex,
is nonempty closed convex,  is closed convex,
is closed convex,  for all
for all  and
and  . At this point, it is sufficient to show that
. At this point, it is sufficient to show that  as
as  . Again, from the proof lines of Theorem 3.1, we have the following conclusions:
. Again, from the proof lines of Theorem 3.1, we have the following conclusions:

Observe that

so that  as
as  . By Theorem 3.1, we have the desired conclusion. This completes the proof.
. By Theorem 3.1, we have the desired conclusion. This completes the proof.
When  in Theorem 3.1, we obtain the following result.
in Theorem 3.1, we obtain the following result.
Corollary 3.6.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  , and let
, and let  be a family of closed and
be a family of closed and  -asymptotically nonexpansive mappings such that
-asymptotically nonexpansive mappings such that  . Assume that every
. Assume that every  ,
,  is asymptotically regular on
is asymptotically regular on  . Let
. Let  be a real sequence in
be a real sequence in  such that
such that  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
When  in Theorem 3.1, we obtain the following result.
in Theorem 3.1, we obtain the following result.
Corollary 3.7.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  , and let
, and let  be a family of closed and
be a family of closed and  -asymptotically nonexpansive mappings such that
-asymptotically nonexpansive mappings such that  . Assume that every
. Assume that every  ,
,  is asymptotically regular on
is asymptotically regular on  . Let
. Let  be a real sequence in
be a real sequence in  such that
such that  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
In the spirit of Theorem 3.1, we can prove the following strong convergence theorem.
Theorem 3.8.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  , and let
, and let  be a family of closed and
be a family of closed and  -nonexpansive mappings such that
-nonexpansive mappings such that  . Let
. Let  ,
,  ,
,  be real sequences in
be real sequences in  such that
such that  ,
,  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
Following the proof lines of Theorem 3.1, we have the following conclusions:
-
(1)
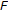 is a nonempty closed convex subset of
is a nonempty closed convex subset of  ;
; -
(2)
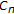 is closed covex for all
is closed covex for all 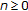 ;
; -
(3)
 , for all
, for all  ;
; -
(4)
 ;
; -
(5)
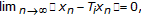 for all
for all  .
.
The closedness property of  together with (4) and (5) implies that
together with (4) and (5) implies that  converges strongly to a common fixed point
converges strongly to a common fixed point  of the family
of the family  . As shown in Theorem 3.1,
. As shown in Theorem 3.1,  . This completes the proof.
. This completes the proof.
When  in Theorem 3.8, we obtain the following result.
in Theorem 3.8, we obtain the following result.
Corollary 3.9.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space, and let
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space, and let  be a family of closed and
be a family of closed and  -nonexpansive mappings such that
-nonexpansive mappings such that  . Let
. Let  be a real sequence in
be a real sequence in  such that
such that  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
When  in Theorem 3.8, we obtain the following result.
in Theorem 3.8, we obtain the following result.
Corollary 3.10.
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  , and let
, and let  be a family of closed and
be a family of closed and  nonexpansive mappings such that
nonexpansive mappings such that  . Let
. Let  be a real sequence in
be a real sequence in  such that
such that  . Define a sequence
. Define a sequence  in
in  in the following manner:
in the following manner:

Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
References
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3
Schu J: Iterative construction of fixed points of asymptotically nonexpansive mappings. Journal of Mathematical Analysis and Applications 1991,158(2):407–413. 10.1016/0022-247X(91)90245-U
Zhou HY, Cho YJ, Kang SM: A new iterative algorithm for approximating common fixed points for asymptotically nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-10.
Haugazeau Y: Sur les inéquations variationnelles et la minimisation de fonctionnelles convexes, Ph.D. thesis. Université de Paris, Paris, France;
Bauschke HH, Combettes PL: A weak-to-strong convergence principle for Fejér-monotone methods in Hilbert spaces. Mathematics of Operations Research 2001,26(2):248–264. 10.1287/moor.26.2.248.10558
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. Journal of Mathematical Analysis and Applications 2003,279(2):372–379. 10.1016/S0022-247X(02)00458-4
Martinez-Yanes C, Xu H-K: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2400–2411. 10.1016/j.na.2005.08.018
Matsushita S, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005,134(2):257–266. 10.1016/j.jat.2005.02.007
Su Y, Qin X: Strong convergence of modified Ishikawa iterations for nonlinear mappings. Proceedings of Indian Academy of Sciences 2007,117(1):97–107. 10.1007/s12044-007-0008-y
Su Y, Wang D, Shang M: Strong convergence of monotone hybrid algorithm for hemi-relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-8.
Zhou H, Gao G, Tan B: Convergence theorems of a modified hybrid algorithm for a family of quasi- φ -asymptotically nonexpansive mappings. Journal of Applied Mathematics and Computing 2010,32(2):453–464. 10.1007/s12190-009-0263-4
Kim T-H, Xu H-K: Strong convergence of modified Mann iterations for asymptotically nonexpansive mappings and semigroups. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1140–1152. 10.1016/j.na.2005.05.059
Kimura Y, Takahashi W: On a hybrid method for a family of relatively nonexpansive mappings in a Banach space. Journal of Mathematical Analysis and Applications 2009,357(2):356–363. 10.1016/j.jmaa.2009.03.052
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Volume 178. Edited by: Kartsatos AG. Dekker, New York, NY, USA; 1996:15–50.
Alber YaI, Reich S: An iterative method for solving a class of nonlinear operator equations in Banach spaces. Panamerican Mathematical Journal 1994,4(2):39–54.
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM Journal on Optimization 2002,13(3):938–945. 10.1137/S105262340139611X
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:xiv+260.
Takahashi W: Nonlinear Functional Analysis, Fixed Point Theory and Its Application. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Mosco U: Convergence of convex sets and of solutions of variational inequalities. Advances in Mathematics 1969, 3: 510–585. 10.1016/0001-8708(69)90009-7
Beer G: Topologies on Closed and Closed Convex Sets, Mathematics and Its Applications. Volume 268. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+340.
Ibaraki T, Kimura Y, Takahashi W: Convergence theorems for generalized projections and maximal monotone operators in Banach spaces. Abstract and Applied Analysis 2003, (10):621–629.
Acknowledgments
This project is supported by the Zhangjiakou city technology research and development projects foundation (0911008B-3), Hebei education department research projects foundation (2006103) and Hebei north university research projects foundation (2009008).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, Y., Zhang, X., Kang, J. et al. Modified Hybrid Algorithm for a Family of Quasi- -Asymptotically Nonexpansive Mappings.
Fixed Point Theory Appl 2010, 170701 (2010). https://doi.org/10.1155/2010/170701
-Asymptotically Nonexpansive Mappings.
Fixed Point Theory Appl 2010, 170701 (2010). https://doi.org/10.1155/2010/170701
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/170701
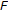 is a nonempty closed convex subset of
is a nonempty closed convex subset of  ;
;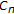 is closed covex for all
is closed covex for all 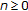 ;
; , for all
, for all  ;
; ;
;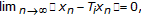 for all
for all  .
.