- Research Article
- Open access
- Published:
Topological Vector Space-Valued Cone Metric Spaces and Fixed Point Theorems
Fixed Point Theory and Applications volume 2010, Article number: 170253 (2010)
Abstract
We develop the theory of topological vector space valued cone metric spaces with nonnormal cones. We prove three general fixed point results in these spaces and deduce as corollaries several extensions of theorems about fixed points and common fixed points, known from the theory of (normed-valued) cone metric spaces. Examples are given to distinguish our results from the known ones.
1. Introduction
Ordered normed spaces and cones have applications in applied mathematics, for instance, in using Newton's approximation method [1–4] and in optimization theory [5].  -metric and
-metric and  -normed spaces were introduced in the mid-20th century ([2], see also [3, 4, 6]) by using an ordered Banach space instead of the set of real numbers, as the codomain for a metric. Huang and Zhang [7] reintroduced such spaces under the name of cone metric spaces but went further, defining convergent and Cauchy sequences in the terms of interior points of the underlying cone. These and other authors (see, e.g., [8–22]) proved some fixed point and common fixed point theorems for contractive-type mappings in cone metric spaces and cone uniform spaces.
-normed spaces were introduced in the mid-20th century ([2], see also [3, 4, 6]) by using an ordered Banach space instead of the set of real numbers, as the codomain for a metric. Huang and Zhang [7] reintroduced such spaces under the name of cone metric spaces but went further, defining convergent and Cauchy sequences in the terms of interior points of the underlying cone. These and other authors (see, e.g., [8–22]) proved some fixed point and common fixed point theorems for contractive-type mappings in cone metric spaces and cone uniform spaces.
In some of the mentioned papers, results were obtained under additional assumptions about the underlying cone, such as normality or even regularity. In the papers [23, 24], the authors tried to generalize this approach by using cones in topological vector spaces (tvs) instead of Banach spaces. However, it should be noted that an old result (see, e.g., [3]) shows that if the underlying cone of an ordered tvs is solid and normal, then such tvs must be an ordered normed space. So, proper generalizations when passing from norm-valued cone metric spaces of [7] to tvs-valued cone metric spaces can be obtained only in the case of nonnormal cones.
In the present paper we develop further the theory of topological vector space valued cone metric spaces (with nonnormal cones). We prove three general fixed point results in these spaces and deduce as corollaries several extensions of theorems about fixed points and common fixed points, known from the theory of (normed-valued) cone metric spaces.
Examples are given to distinguish our results from the known ones.
2. Tvs-Valued Cone Metric Spaces
Let  be a real Hausdorff topological vector space (tvs for short) with the zero vector
be a real Hausdorff topological vector space (tvs for short) with the zero vector  . A proper nonempty and closed subset
. A proper nonempty and closed subset  of
of  is called a (convex) cone if
is called a (convex) cone if  ,
,  for
for  and
and  . We will always assume that the cone P has a nonempty interior int P (such cones are called solid).
. We will always assume that the cone P has a nonempty interior int P (such cones are called solid).
Each cone  induces a partial order
induces a partial order  on
on  by
by  .
.  will stand for
will stand for  and
and  , while
, while  will stand for
will stand for  . The pair
. The pair  is an ordered topological vector space.
is an ordered topological vector space.
For a pair of elements  in
in  such that
such that  , put
, put

The sets of the form  are called order intervals. It is easily verified that order-intervals are convex. A subset
are called order intervals. It is easily verified that order-intervals are convex. A subset  of
of  is said to be order-convex if
is said to be order-convex if  , whenever
, whenever  and
and  .
.
Ordered topological vector space  is order-convex if it has a base of neighborhoods of
is order-convex if it has a base of neighborhoods of  consisting of order-convex subsets. In this case the cone
consisting of order-convex subsets. In this case the cone  is said to be normal. In the case of a normed space, this condition means that the unit ball is order-convex, which is equivalent to the condition that there is a number
is said to be normal. In the case of a normed space, this condition means that the unit ball is order-convex, which is equivalent to the condition that there is a number  such that
such that  and
and  implies that
implies that  . Another equivalent condition is that
. Another equivalent condition is that

It is not hard to conclude from (2.2) that  is a nonnormal cone in a normed space
is a nonnormal cone in a normed space  if and only if there exist sequences
if and only if there exist sequences  such that
such that

Hence, in this case, the Sandwich theorem does not hold.
Note the following properties of bounded sets.
If the cone  is solid, then each topologically bounded subset of
is solid, then each topologically bounded subset of  is also order-bounded, that is, it is contained in a set of the form
is also order-bounded, that is, it is contained in a set of the form  for some
for some  .
.
If the cone  is normal, then each order-bounded subset of
is normal, then each order-bounded subset of  is topologically bounded. Hence, if the cone is both solid and normal, these two properties of subsets of
is topologically bounded. Hence, if the cone is both solid and normal, these two properties of subsets of  coincide. Moreover, a proof of the following assertion can be found, for example, in [3].
coincide. Moreover, a proof of the following assertion can be found, for example, in [3].
Theorem 2.1.
If the underlying cone of an ordered tvs is solid and normal, then such tvs must be an ordered normed space.
Example 2.2.
(see [5]) Let  with
with  , and let
, and let  . This cone is solid (it has the nonempty interior) but is not normal. Consider, for example,
. This cone is solid (it has the nonempty interior) but is not normal. Consider, for example,  ) and
) and  ). Since
). Since  and
and  , it follows that
, it follows that  is a nonnormal cone.
is a nonnormal cone.
Now consider the space  endowed with the strongest locally convex topology
endowed with the strongest locally convex topology  . Then
. Then  is also
is also  -solid (it has the nonempty
-solid (it has the nonempty  -interior), but not
-interior), but not  -normal. Indeed, if it were normal then, according to Theorem 2.1, the space
-normal. Indeed, if it were normal then, according to Theorem 2.1, the space  would be normed, which is impossible since an infinite-dimensional space with the strongest locally convex topology cannot be metrizable (see, e.g., [25]).
would be normed, which is impossible since an infinite-dimensional space with the strongest locally convex topology cannot be metrizable (see, e.g., [25]).
Following [7, 23, 24] we give the following.
Definition 2.3.
Let  be a nonempty set and
be a nonempty set and  an ordered tvs. A function
an ordered tvs. A function  is called a tvs-cone metric and
is called a tvs-cone metric and  is called a tvs-cone metric, space if the following conditions hold:
is called a tvs-cone metric, space if the following conditions hold:

 for all
for all  and
and  if and only if
if and only if  ;
;

 for all
for all  ;
;

 for all
for all  .
.
Let  and
and  be a sequence in
be a sequence in  . Then it is said the following.
. Then it is said the following.
(i) tvs-cone converges to
tvs-cone converges to  if for every
if for every  with
with  there exists a natural number
there exists a natural number  such that
such that  for all
for all  ; we denote it by
; we denote it by  or
or  as
as  .
.
(ii) is a tvs-cone Cauchy sequence if for every
is a tvs-cone Cauchy sequence if for every  with
with  there exists a natural number
there exists a natural number  such that
such that  for all
for all  .
.
(iii) is tvs-cone complete if every tvs-Cauchy sequence is tvs-convergent in
is tvs-cone complete if every tvs-Cauchy sequence is tvs-convergent in  .
.
Taking into account Theorem 2.1, proper generalizations when passing from norm-valued cone metric spaces of [7] to tvs-cone metric spaces can be obtained only in the case of nonnormal cones.
We will prove now some properties of a real tvs with a solid cone
with a solid cone  and a tvs-cone metric space
and a tvs-cone metric space  over it.
over it.
Lemma 2.4.
-
(a)
Let
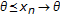 in
in  , and let
, and let  . Then there exists
. Then there exists 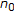 such that
such that  for each
for each 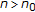 .
. -
(b)
It can happen that
 for each
for each  , but
, but 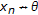 in
in 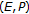 .
. -
(c)
It can happen that
 ,
, 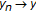 in the tvs-cone metric
in the tvs-cone metric  , but that
, but that 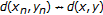 in
in 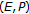 . In particular, it can happen that
. In particular, it can happen that  in
in 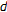 but that
but that  (which is impossible if the cone is normal).
(which is impossible if the cone is normal). -
(d)
 for each
for each  implies that
implies that  .
. -
(e)
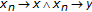 (in the tvs-cone metric) implies that
(in the tvs-cone metric) implies that 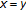 .
. -
(f)
Each tvs-cone metric space is Hausdorff in the sense that for arbitrary distinct points
 and
and  there exist disjoint neighbourhoods in the topology
there exist disjoint neighbourhoods in the topology  having the local base formed by the sets of the form
having the local base formed by the sets of the form  ,
, 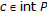 .
.
Proof.
-
(a)
It follows from
 that
that 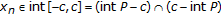 for
for 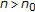 . From
. From  , it follows that
, it follows that  , that is,
, that is,  .
. -
(b)
Consider the sequences
 ) and
) and  ) from Example 2.2. We know that in the ordered Banach space
) from Example 2.2. We know that in the ordered Banach space 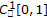
 (2.4)
(2.4)
and that  (in the norm of
(in the norm of  ) but that
) but that  in this norm. On the other hand, since
in this norm. On the other hand, since  and
and  , it follows that
, it follows that  . Then also
. Then also  in the tvs
in the tvs (the strongest locally convex topology) but
(the strongest locally convex topology) but  (also considering the interior with respect to
(also considering the interior with respect to  ).
).
We can also consider the tvs-cone metric  defined by
defined by  ,
,  , and
, and  . Then for the sequence
. Then for the sequence  we have that
we have that  in the tvs-cone metric, since
in the tvs-cone metric, since  , but
, but  in the tvs
in the tvs for otherwise it would tend to
for otherwise it would tend to  in the norm of the space
in the norm of the space  .
.
-
(c)
Take the sequence
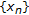 from (b) and
from (b) and  . Then
. Then 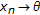 , and
, and  in the cone metric
in the cone metric 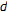 since
since  and
and 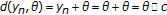 , but
, but 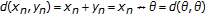 in
in  . This means that a tvs-cone metric may be a discontinuous function.
. This means that a tvs-cone metric may be a discontinuous function. -
(d)
The proof is the same as in the Banach case. For an arbitrary
 , it is
, it is 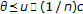 for each
for each  , and passing to the limit in
, and passing to the limit in  it follows that
it follows that  , that is,
, that is, 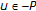 . Since
. Since  is a cone it follows that
is a cone it follows that  .
. -
(e)
From
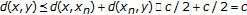 for each
for each  it follows that
it follows that  (for arbitrary
(for arbitrary 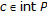 ), which, by (d), means that
), which, by (d), means that 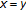 .
. -
(f)
Suppose, to the contrary, that for the given distinct points
 and
and 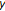 there exists a point
there exists a point  . Then
. Then  for arbitrary
for arbitrary 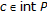 , implying that
, implying that 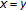 , a contradiction.
, a contradiction.
The following properties, which can be proved in the same way as in the normed case, will also be needed.
Lemma 2.5.
-
(a)
If
 and
and  , then
, then 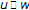 .
. -
(b)
If
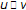 and
and  , then
, then  .
. -
(c)
If
 and
and  , then
, then  .
. -
(d)
Let
 ,
, 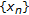 and
and 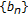 be two sequences in
be two sequences in  and
and  , respectively,
, respectively,  , and
, and 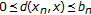 for all
for all  . If
. If  , then there exists a natural number
, then there exists a natural number  such that
such that 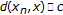 for all
for all  .
.
3. Fixed Point and Common Fixed Point Results
Theorem 3.1.
Let  be a tvs-cone metric space and the mappings
be a tvs-cone metric space and the mappings  satisfy
satisfy

for all  , where
, where  ,
,  , and
, and  or
or  . If
. If  and
and  is a complete subspace of
is a complete subspace of  , then
, then  ,
,  , and
, and  have a unique point of coincidence. Moreover, if
have a unique point of coincidence. Moreover, if  and
and  are weakly compatible, then
are weakly compatible, then  ,
,  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Recall that a point  is called a coincidence point of the pair
is called a coincidence point of the pair  and
and  is its point of coincidence if
is its point of coincidence if  . The pair
. The pair  is said to be weakly compatible if for each
is said to be weakly compatible if for each  ,
,  implies that
implies that  .
.
Proof.
Let  be arbitrary. Using the condition
be arbitrary. Using the condition  choose a sequence
choose a sequence  such that
such that  and
and  for all
for all  . Applying contractive condition (3.1) we obtain that
. Applying contractive condition (3.1) we obtain that

It follows that

that is,

In a similar way one obtains that

Now, from (3.4) and (3.5), by induction, we obtain that

Let

In the case  ,
,

and if  ,
,

Now, for  , we have
, we have

Similarly, we obtain

Hence, for 

where  , as
, as  .
.
Now, using properties (a) and (d) from Lemma 2.5 and only the assumption that the underlying cone is solid, we conclude that  is a Cauchy sequence. Since the subspace
is a Cauchy sequence. Since the subspace  is complete, there exist
is complete, there exist  such that
such that  (
( ).
).
We will prove that  . Firstly, let us estimate that
. Firstly, let us estimate that  . We have that
. We have that

By the contractive condition (3.1), it holds that

Now it follows from (3.13) that

that is,

Let  . Then there exists
. Then there exists  such that for
such that for  it holds that
it holds that

and  , that is,
, that is,  for
for  . Since
. Since  was arbitrary, it follows that
was arbitrary, it follows that  , that is,
, that is,  .
.
Similarly using that

it can be deduced that  . It follows that
. It follows that  is a common point of coincidence for
is a common point of coincidence for  ,
,  , and
, and  , that is,
, that is,

Now we prove that the point of coincidence of  is unique. Suppose that there is another point
is unique. Suppose that there is another point  such that
such that

for some  . Using the contractive condition we obtain that
. Using the contractive condition we obtain that

Since  , it follows that
, it follows that  , that is,
, that is,  .
.
Using weak compatibility of the pairs  and
and  and proposition 1.12 from [16], it follows that the mappings
and proposition 1.12 from [16], it follows that the mappings  have a unique common fixed point, that is,
have a unique common fixed point, that is,  .
.
Corollary 3.2.
Let  be a tvs-cone metric space and the mappings
be a tvs-cone metric space and the mappings  satisfy
satisfy

for all  , where
, where  and
and  . If
. If  and
and  is a complete subspace of
is a complete subspace of  , then
, then  , and
, and  have a unique point of coincidence. Moreover, if
have a unique point of coincidence. Moreover, if  and
and  are weakly compatible, then
are weakly compatible, then  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Putting in this corollary  and taking into account that each self-map is weakly compatible with the identity mapping, we obtain the following.
and taking into account that each self-map is weakly compatible with the identity mapping, we obtain the following.
Corollary 3.3.
Let  be a complete tvs-cone metric space, and let the mappings
be a complete tvs-cone metric space, and let the mappings  satisfy
satisfy

for all  , where
, where  and
and  . Then
. Then  and
and  have a unique common fixed point in
have a unique common fixed point in  . Moreover, any fixed point of
. Moreover, any fixed point of  is a fixed point of
is a fixed point of  , and conversely.
, and conversely.
In the case of a cone metric space with a normal cone, this result was proved in [14].
Now put first  in Theorem 3.1 and then
in Theorem 3.1 and then  . Choosing appropriate values for coefficients, we obtain the following.
. Choosing appropriate values for coefficients, we obtain the following.
Corollary 3.4.
Let  be a tvs-cone metric space. Suppose that the mappings
be a tvs-cone metric space. Suppose that the mappings  satisfy the contractive condition
satisfy the contractive condition


or

for all  , where
, where  is a constant (
is a constant ( in (3.24) and
in (3.24) and  in (3.25) and (3.26)). If
in (3.25) and (3.26)). If  and
and  is a complete subspace of
is a complete subspace of  , then
, then  and
and  have a unique point of coincidence in
have a unique point of coincidence in  . Moreover, if
. Moreover, if  and
and  are weakly compatible, then
are weakly compatible, then  and
and  have a unique common fixed point.
have a unique common fixed point.
In the case when the space  is normed and the cone
is normed and the cone  is normal, these results were proved in [9].
is normal, these results were proved in [9].
Similarly one obtains the following.
Corollary 3.5.
Let  be a tvs-cone metric space, and let
be a tvs-cone metric space, and let  be such that
be such that  . Suppose that
. Suppose that

for all  , where
, where  and
and  , and let
, and let  imply that
imply that  for each
for each  . If
. If  or
or  is a complete subspace of
is a complete subspace of  , then the mappings
, then the mappings  and
and  have a unique common fixed point in
have a unique common fixed point in  . Moreover, for any
. Moreover, for any  , the
, the  -
- -sequence
-sequence  with the initial point
with the initial point  converges to the fixed point.
converges to the fixed point.
Here, an  -
- -sequence (also called a Jungck sequence)
-sequence (also called a Jungck sequence)  is formed in the following way. Let
is formed in the following way. Let  be arbitrary. Since
be arbitrary. Since  , there exists
, there exists  such that
such that  . Having chosen
. Having chosen  ,
,  is chosen such that
is chosen such that  .
.
In the case when the space  is normed and under the additional assumption that the cone
is normed and under the additional assumption that the cone  is normal, these results were firstly proved in [10].
is normal, these results were firstly proved in [10].
Corollary 3.6.
Let  be a complete tvs-cone metric space. Suppose that the mapping
be a complete tvs-cone metric space. Suppose that the mapping  satisfies the contractive condition
satisfies the contractive condition


or

for all  , where
, where  is a constant (
is a constant ( in (3.28) and
in (3.28) and  in (3.29) and (3.30)). Then
in (3.29) and (3.30)). Then  has a unique fixed point in
has a unique fixed point in  , and for any
, and for any  , the iterative sequence
, the iterative sequence  converges to the fixed point.
converges to the fixed point.
In the case when the space  is normed and under the additional assumption that the cone
is normed and under the additional assumption that the cone  is normal, these results were firstly proved in [7]. The normality condition was removed in [8].
is normal, these results were firstly proved in [7]. The normality condition was removed in [8].
Finally, we give an example of a situation where Theorem 3.1 can be applied, while the results known so far cannot.
Example 3.7 (see [26, Example  ]).
]).
Let  ,
,  with the cone
with the cone  as in Example
as in Example  and endowed with the strongest locally convex topology
and endowed with the strongest locally convex topology  . Let the metric
. Let the metric  be defined by
be defined by  if
if  and
and  ,
,  , and
, and  . Further, let
. Further, let  be given by,
be given by,  ,
,  and
and  ,
,  . Finally, let
. Finally, let  .
.
Taking  ,
,  , all the conditions of Theorem 3.1 are fulfilled. Indeed, since
, all the conditions of Theorem 3.1 are fulfilled. Indeed, since  , we have only to check that
, we have only to check that

which is equivalent to

Hence, we can apply Theorem 3.1 and conclude that the mappings  have a unique common fixed point (
have a unique common fixed point ( ).
).
On the other hand, since the space  is not an ordered Banach space and its cone is not normal, neither of the mentioned results from [7–10, 14] can be used to obtain such conclusion. Thus, Theorem 3.1 and its corollaries are proper extensions of these results.
is not an ordered Banach space and its cone is not normal, neither of the mentioned results from [7–10, 14] can be used to obtain such conclusion. Thus, Theorem 3.1 and its corollaries are proper extensions of these results.
Note that an example of similar kind is also given in [24].
The following example shows that the condition " or
or  " in Theorem 3.1 cannot be omitted.
" in Theorem 3.1 cannot be omitted.
Example 3.8 (see [26, Example  ]).
]).
Let  , where
, where  ,
,  ,
,  , and
, and  . Let
. Let  be the Euclidean metric in
be the Euclidean metric in  , and let the tvs-cone metric
, and let the tvs-cone metric  (
( ,
,  , and
, and  are as in the previous example) be defined in the following way:
are as in the previous example) be defined in the following way:  , where
, where  is a fixed function, for example,
is a fixed function, for example,  . Consider the mappings
. Consider the mappings

and let  . By a careful computation it is easy to obtain that
. By a careful computation it is easy to obtain that

for all  . We will show that
. We will show that  and
and  satisfy the following contractive condition: there exist
satisfy the following contractive condition: there exist  with
with  and
and  ,
,  such that
such that

holds true for all  . Obviously,
. Obviously,  and
and  do not have a common fixed point.
do not have a common fixed point.
Taking (3.34) into account, we have to consider the following cases.
(1)In case  , then (3.35) holds for
, then (3.35) holds for  ,
,  and
and  .
.
(2)In case  , then (3.35) holds for
, then (3.35) holds for  ,
,  and
and  .
.
(3)In case  , then (3.35) holds for
, then (3.35) holds for  ,
,  and
and  .
.
(4)In case  , then (3.35) holds for
, then (3.35) holds for  ,
,  and
and  .
.
(5)In case  , then (3.35) holds for
, then (3.35) holds for  ,
,  and
and  .
.
4. Quasicontractions in Tvs-Cone Metric Spaces
Definition 4.1.
Let  be a tvs-cone metric space, and let
be a tvs-cone metric space, and let  . Then,
. Then,  is called a quasi-contraction (resp., a
is called a quasi-contraction (resp., a  -quasi-contraction) if for some constant
-quasi-contraction) if for some constant  and for all
and for all  , there exists
, there exists

such that

Theorem 4.2.
Let  be a complete tvs-cone metric space, and let
be a complete tvs-cone metric space, and let  be such that
be such that  and
and  is closed. If
is closed. If  is a
is a  -quasi-contraction with
-quasi-contraction with  , then
, then  and
and  have a unique point of coincidence. Moreover, if the pair
have a unique point of coincidence. Moreover, if the pair  is weakly compatible or, at least, occasionally weakly compatible, then
is weakly compatible or, at least, occasionally weakly compatible, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Recall that the pair  of self-maps on
of self-maps on  is called occasionally weakly compatible (see [27] or [28]) if there exists
is called occasionally weakly compatible (see [27] or [28]) if there exists  such that
such that  and
and  .
.
Proof.
Let us remark that the condition  implies that starting with an arbitrary
implies that starting with an arbitrary  , we can construct a sequence
, we can construct a sequence  of points in
of points in  such that
such that  for all
for all  . We will prove that
. We will prove that  is a Cauchy sequence. First, we show that
is a Cauchy sequence. First, we show that

for all  . Indeed,
. Indeed,

where

The following four cases may occur:
(1)First,  .
.
(2)Second,  and so
and so  . In this case, (4.3) follows immediately, because
. In this case, (4.3) follows immediately, because  ).
).
(3)Third,  . It follows that (4.3) holds.
. It follows that (4.3) holds.
(4)Fourth,  and so
and so  . Hence, (4.3) holds.
. Hence, (4.3) holds.
Thus, by putting  , we have that
, we have that  . Now, using (4.3), we have
. Now, using (4.3), we have

for all  . It follows that
. It follows that

Using properties (a) and (d) from Lemma 2.5, we obtain that  is a Cauchy sequence. Therefore, since
is a Cauchy sequence. Therefore, since  is complete and
is complete and  is closed, there exists
is closed, there exists  such that
such that

Now we will show that  .
.
By the definition of  -quasicontraction, we have that
-quasicontraction, we have that

where  . Observe that
. Observe that  and
and  . Now let
. Now let  be given. In all of the possible five cases there exists
be given. In all of the possible five cases there exists  such that (using (4.9)) one obtains that
such that (using (4.9)) one obtains that  :
:
(1) ;
;
(2) ;
;
(3) ; it follows that
; it follows that  ;
;
(4) ;
;
(5) ; it follows that
; it follows that  .
.
It follows that  (
( ). The uniqueness of limit in a cone metric space implies that
). The uniqueness of limit in a cone metric space implies that  . Thus,
. Thus,  is a coincidence point of the pair
is a coincidence point of the pair  , and
, and  is its point of coincidence. It can be showed in a standard way that this point of coincidence is unique. Using lemma 1.6 of [27] one readily obtains that, in the case when the pair
is its point of coincidence. It can be showed in a standard way that this point of coincidence is unique. Using lemma 1.6 of [27] one readily obtains that, in the case when the pair  is occasionally weakly compatible, the point
is occasionally weakly compatible, the point  is the unique common fixed point of
is the unique common fixed point of  and
and  .
.
In the normed case and assuming that the cone is normal (but letting  ), this theorem was proved in [11].
), this theorem was proved in [11].
Puting  in Theorem 4.2 we obtain the following.
in Theorem 4.2 we obtain the following.
Corollary 4.3.
Let  be a complete tvs-cone metric space, and let the mapping
be a complete tvs-cone metric space, and let the mapping  be a quasi-contraction with
be a quasi-contraction with  . Then
. Then  has a unique fixed point in
has a unique fixed point in  , and for any
, and for any  , the iterative sequence
, the iterative sequence  converges to the fixed point.
converges to the fixed point.
In the case of normed-valued cone metric spaces and under the assumption that the underlying cone  is normal (and with
is normal (and with  ), this result was obtained in [12]. Normality condition was removed in [13].
), this result was obtained in [12]. Normality condition was removed in [13].
From Theorem 4.2, as corollaries, among other things, we again recover and extend the results of Huang and Zhang [7] and Rezapour and Hamlbarani [8]. The following three corollaries follow in a similar way.
In the next corollary, we extend the well-known result [29, (9')].
Corollary 4.4.
Let  be a complete tvs-cone metric space, and let
be a complete tvs-cone metric space, and let  be such that
be such that  and
and  is closed. Further, let for some constant
is closed. Further, let for some constant  and every
and every  there exists
there exists

such that

Then  and
and  have a unique point of coincidence. Moreover, if the pair
have a unique point of coincidence. Moreover, if the pair  is occasionally weakly compatible, then they have a unique common fixed point.
is occasionally weakly compatible, then they have a unique common fixed point.
We can also extend the well-known Bianchini's result [29, (5)]
Corollary 4.5.
Let  be a complete tvs-cone metric space, and let
be a complete tvs-cone metric space, and let  be such that
be such that  and
and  is closed. Further, let for some constant
is closed. Further, let for some constant  and every
and every  , there exists
, there exists

such that

Then  and
and  have a unique point of coincidence. Moreover, if the pair
have a unique point of coincidence. Moreover, if the pair  is occasionally weakly compatible, then they have a unique common fixed point.
is occasionally weakly compatible, then they have a unique common fixed point.
In the next corollary, we extend the well-known result of Jungck [30, Theorem  ].
].
Corollary 4.6.
Let  be a complete tvs-cone metric space, and let
be a complete tvs-cone metric space, and let  be such that
be such that  and
and  is closed. Further, let for some constant
is closed. Further, let for some constant  and every
and every  ,
,

Then  and
and  have a unique point of coincidence. Moreover, if the pair
have a unique point of coincidence. Moreover, if the pair  is occasionally weakly compatible, then they have a unique common fixed point.
is occasionally weakly compatible, then they have a unique common fixed point.
Remark 4.7.
Note that in the previous three corollaries it is possible that the parameter  takes values from
takes values from  (and not only in
(and not only in  as in Theorem 4.2). Namely, it is possible to show that the sequence
as in Theorem 4.2). Namely, it is possible to show that the sequence  used in the proof, is a Cauchy sequence because the condition on
used in the proof, is a Cauchy sequence because the condition on  is stronger.
is stronger.
Now, we prove the main result of Das and Naik [31] in the frame of tvs-cone metric spaces in which the cone need not be normal.
Theorem 4.8.
Let  be a complete tvs-cone metric space. Let
be a complete tvs-cone metric space. Let  be a self-map on
be a self-map on  such that
such that  is continuous, and let
is continuous, and let  be any self-map on
be any self-map on  that commutes with
that commutes with  . Further let
. Further let  and
and  satisfy
satisfy

and let  be a
be a  -quasi-contraction. Then
-quasi-contraction. Then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By (4.15), starting with an arbitrary  , we can construct a sequence
, we can construct a sequence  of points in
of points in  such that
such that  ,
,  (as in Theorem 4.2). Now
(as in Theorem 4.2). Now  ,
,  . It can be proved as in Theorem 4.2 that
. It can be proved as in Theorem 4.2 that  is a Cauchy sequence and hence convergent to some
is a Cauchy sequence and hence convergent to some  . Further, we will show that
. Further, we will show that  . Since
. Since

it follows that

because  is continuous. Now, we obtain
is continuous. Now, we obtain

where

Let  be given. Since
be given. Since  and
and  , choose a natural number
, choose a natural number  such that for all
such that for all  we have
we have  and
and  . Again, we have the following cases:
. Again, we have the following cases:
-
(a)
 (4.20)
(4.20)
-
(b)
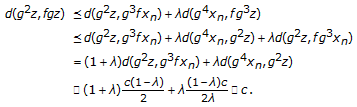 (4.21)
(4.21)
-
(c)
 (4.22)
(4.22)
-
(d)
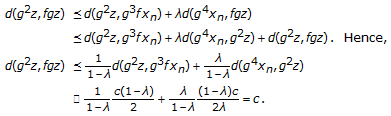 (4.23)
(4.23)
-
(e)
 (4.24)
(4.24)
Therefore,  for all
for all  . By property (d) of Lemma 2.4,
. By property (d) of Lemma 2.4,  , and so
, and so  is a common fixed point for
is a common fixed point for  and
and  . Indeed, putting in the contractivity condition
. Indeed, putting in the contractivity condition  , we get
, we get  . Since
. Since  , that is,
, that is,  , we have that
, we have that  .
.
References
Kantorovič LV: The principle of the majorant and Newton's method. Doklady Akademii Nauk SSSR 1951, 76: 17–20.
Kantorovitch LV: On some further applications of the Newton approximation method. Vestnik Leningrad University. Mathematics 1957,12(7):68–103.
Vandergraft JS: Newton's method for convex operators in partially ordered spaces. SIAM Journal on Numerical Analysis 1967, 4: 406–432. 10.1137/0704037
Zabrejko PP:
 -metric and
-metric and  -normed linear spaces: survey Collectanea Mathematica 1997,48(4–6):825–859.
-normed linear spaces: survey Collectanea Mathematica 1997,48(4–6):825–859.Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Aliprantis CD, Tourky R: Cones and Duality, Graduate Studies in Mathematics. Volume 84. American Mathematical Society, Providence, RI, USA; 2007:xiv+279.
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Rezapour S, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. Journal of Mathematical Analysis and Applications 2008,341(1):416–420. 10.1016/j.jmaa.2007.09.070
Vetro P: Common fixed points in cone metric spaces. Rendiconti del Circolo Matematico di Palermo. Serie II 2007,56(3):464–468. 10.1007/BF03032097
Ilić D, Rakočević V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Ilić D, Rakočević V: Quasi-contraction on a cone metric space. Applied Mathematics Letters 2009,22(5):728–731. 10.1016/j.aml.2008.08.011
Kadelburg Z, Radenović S, Rakočević V: Remarks on "Quasi-contraction on a cone metric space". Applied Mathematics Letters 2009,22(11):1674–1679. 10.1016/j.aml.2009.06.003
Abbas M, Rhoades BE: Fixed and periodic point results in cone metric spaces. Applied Mathematics Letters 2009,22(4):511–515. 10.1016/j.aml.2008.07.001
Janković S, Kadelburg Z, Radenović S, Rhoades BE: Assad-Kirk-type fixed point theorems for a pair of nonself mappings on cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-16.
Jungck G, Radenović S, Radojević S, Rakočević V: Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-13.
Kadelburg Z, Radenović S, Rosić B: Strict contractive conditions and common fixed point theorems in cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-14.
Włodarczyk K, Plebaniak R: Periodic point, endpoint, and convergence theorems for dissipative set-valued dynamic systems with generalized pseudodistances in cone uniform and uniform spaces. Fixed Point Theory and Applications 2010, 2010:-32.
Włodarczyk K, Plebaniak R: Maximality principle and general results of ekeland and caristi types without lower semicontinuity assumptions in cone uniform spaces with generalized pseudodistances. Fixed Point Theory and Applications 2010, 2010:-37.
Włodarczyk K, Plebaniak R, Doliński M: Cone uniform, cone locally convex and cone metric spaces, endpoints, set-valued dynamic systems and quasi-asymptotic contractions. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):5022–5031. 10.1016/j.na.2009.03.076
Włodarczyk K, Plebaniak R, Obczyński C: Convergence theorems, best approximation and best proximity for set-valued dynamic systems of relatively quasi-asymptotic contractions in cone uniform spaces. Nonlinear Analysis: Theory, Methods & Applications 2010,72(2):794–805. 10.1016/j.na.2009.07.024
Azam A, Arshad M, Beg I: Existence of fixed points in complete cone metric spaces. International Journal of Modern Mathematics 2010,5(1):91–99.
Du W-S: A note on cone metric fixed point theory and its equivalence. Nonlinear Analysis: Theory, Methods & Applications 2010,72(5):2259–2261. 10.1016/j.na.2009.10.026
Beg I, Azam A, Arshad M: Common fixed points for maps on topological vector space valued cone metric spaces. International Journal of Mathematics and Mathematical Sciences 2009, 2009:-8.
Schaefer HH: Topological Vector Spaces. 3rd edition. Springer, New York, NY, USA; 1971:xi+294.
Kadelburg Z, Pavlović M, Radenović S: Common fixed point theorems for ordered contractions and quasicontractions in ordered cone metric spaces. Computers & Mathematics with Applications 2010,59(9):3148–3159. 10.1016/j.camwa.2010.02.039
Jungck G, Rhoades BE: Fixed point theorems for occasionally weakly compatible mappings. Fixed Point Theory 2006,7(2):287–296.
Al-Thagafi MA, Shahzad N: Generalized -nonexpansive selfmaps and invariant approximations. Acta Mathematica Sinica 2008,24(5):867–876. 10.1007/s10114-007-5598-x
Rhoades BE: A comparison of various definitions of contractive mappings. Transactions of the American Mathematical Society 1977, 226: 257–290.
Jungck G: Commuting mappings and fixed points. The American Mathematical Monthly 1976,83(4):261–263. 10.2307/2318216
Das KM, Naik KV: Common fixed-point theorems for commuting maps on a metric space. Proceedings of the American Mathematical Society 1979,77(3):369–373.
Acknowledgments
The authors are very grateful to the referees for the valuable comments that enabled them to revise this paper. They are thankful to the Ministry of Science and Technological Development of Serbia.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kadelburg, Z., Radenović, S. & Rakočević, V. Topological Vector Space-Valued Cone Metric Spaces and Fixed Point Theorems. Fixed Point Theory Appl 2010, 170253 (2010). https://doi.org/10.1155/2010/170253
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/170253
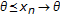 in
in  , and let
, and let  . Then there exists
. Then there exists 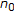 such that
such that  for each
for each 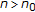 .
. for each
for each  , but
, but 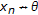 in
in 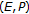 .
. ,
, 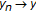 in the tvs-cone metric
in the tvs-cone metric  , but that
, but that 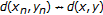 in
in 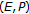 . In particular, it can happen that
. In particular, it can happen that  in
in 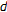 but that
but that  (which is impossible if the cone is normal).
(which is impossible if the cone is normal). for each
for each  implies that
implies that  .
.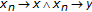 (in the tvs-cone metric) implies that
(in the tvs-cone metric) implies that 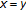 .
. and
and  there exist disjoint neighbourhoods in the topology
there exist disjoint neighbourhoods in the topology  having the local base formed by the sets of the form
having the local base formed by the sets of the form  ,
, 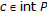 .
. that
that 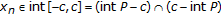 for
for 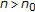 . From
. From  , it follows that
, it follows that  , that is,
, that is,  .
. ) and
) and  ) from Example 2.2. We know that in the ordered Banach space
) from Example 2.2. We know that in the ordered Banach space 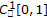

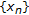 from (b) and
from (b) and  . Then
. Then 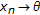 , and
, and  in the cone metric
in the cone metric 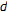 since
since  and
and 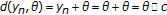 , but
, but 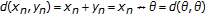 in
in  . This means that a tvs-cone metric may be a discontinuous function.
. This means that a tvs-cone metric may be a discontinuous function. , it is
, it is 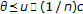 for each
for each  , and passing to the limit in
, and passing to the limit in  it follows that
it follows that  , that is,
, that is, 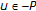 . Since
. Since  is a cone it follows that
is a cone it follows that  .
.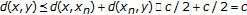 for each
for each  it follows that
it follows that  (for arbitrary
(for arbitrary 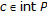 ), which, by (d), means that
), which, by (d), means that 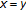 .
. and
and 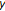 there exists a point
there exists a point  . Then
. Then  for arbitrary
for arbitrary 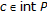 , implying that
, implying that 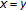 , a contradiction.
, a contradiction. and
and  , then
, then 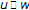 .
.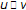 and
and  , then
, then  .
. and
and  , then
, then  .
. ,
, 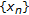 and
and 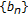 be two sequences in
be two sequences in  and
and  , respectively,
, respectively,  , and
, and 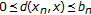 for all
for all  . If
. If  , then there exists a natural number
, then there exists a natural number  such that
such that 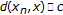 for all
for all  .
.
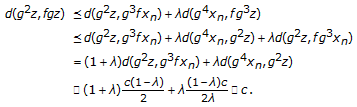

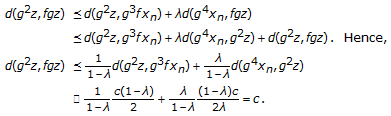

 -metric and
-metric and  -normed linear spaces: survey Collectanea Mathematica 1997,48(4–6):825–859.
-normed linear spaces: survey Collectanea Mathematica 1997,48(4–6):825–859.