- Research Article
- Open access
- Published:
Strong Convergence Theorems for Infinitely Nonexpansive Mappings in Hilbert Space
Fixed Point Theory and Applications volume 2009, Article number: 962303 (2009)
Abstract
We introduce a modified Ishikawa iterative process for approximating a fixed point of two infinitely nonexpansive self-mappings by using the hybrid method in a Hilbert space and prove that the modified Ishikawa iterative sequence converges strongly to a common fixed point of two infinitely nonexpansive self-mappings.
1. Introduction
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  ,
,  a self-mapping of
a self-mapping of  . Recall that
. Recall that  is said to be nonexpansive if
is said to be nonexpansive if  for all
for all  .
.
Construction of fixed points of nonexpansive mappings via Mann's iteration [1] has extensively been investigated in literature (see, e.g., [2–5] and reference therein). But the convergence about Mann's iteration and Ishikawa's iteration is in general not strong (see the counterexample in [6]). In order to get strong convergence, one must modify them. In 2003, Nakajo and Takahashi [7] proposed such a modification for a nonexpansive mapping  .
.
Consider the algorithm,

where  denotes the metric projection from
denotes the metric projection from  onto a closed convex subset
onto a closed convex subset  of
of  . They prove the sequence
. They prove the sequence  generated by that algorithm (1.1) converges strongly to a fixed point of
generated by that algorithm (1.1) converges strongly to a fixed point of  provided that the control sequence
provided that the control sequence  is chosen so that
is chosen so that  .
.
Let  be a sequence of nonexpansive self-mappings of
be a sequence of nonexpansive self-mappings of  ,
,  a sequence of nonnegative numbers in
a sequence of nonnegative numbers in  . For each
. For each  , defined a mapping
, defined a mapping  of
of  into itself as follows:
into itself as follows:

Such a mapping  is called the
is called the  -mapping generated by
-mapping generated by  and
and  ; see [8].
; see [8].
In this paper, motivated by [9], for any given  (
( is a fixed number), we will propose the following iterative progress for two infinitely nonexpansive mappings
is a fixed number), we will propose the following iterative progress for two infinitely nonexpansive mappings  and
and  in a Hilbert space
in a Hilbert space  :
:

and prove,  converges strongly to a fixed point of
converges strongly to a fixed point of  and
and  .
.
We will use the notation:
 for weak convergence and
for weak convergence and  for strong convergence.
for strong convergence.
 denotes the weak
denotes the weak  -limit set of
-limit set of  .
.
2. Preliminaries
In this paper, we need some facts and tools which are listed as lemmas below.
Lemma 2.1 (see [10]).
Let  be a Hilbert space,
be a Hilbert space,  a nonempty closed convex subset of
a nonempty closed convex subset of  , and
, and  a nonexpansive mapping with Fix
a nonexpansive mapping with Fix . If
. If  is a sequence in
is a sequence in  weakly converging to
weakly converging to  and if
and if  converges strongly to
converges strongly to  , then
, then  .
.
Lemma 2.2 (see [11]).
Let  be a nonempty bounded closed convex subset of a Hilbert space
be a nonempty bounded closed convex subset of a Hilbert space  . Given also a real number
. Given also a real number  and
and  . Then the set
. Then the set  is closed and convex.
is closed and convex.
Let  be a sequence of nonexpansive self-mappings on
be a sequence of nonexpansive self-mappings on  , where
, where  is a nonempty closed convex subset of a strictly convex Banach space
is a nonempty closed convex subset of a strictly convex Banach space  . Given a sequence
. Given a sequence  in
in  , one defines a sequence
, one defines a sequence  of self-mappings on
of self-mappings on  by (1.2). Then one has the following results.
by (1.2). Then one has the following results.
Lemma 2.3 (see [8]).
Let  be a nonempty closed convex subset of a strictly convex Banach space
be a nonempty closed convex subset of a strictly convex Banach space  ,
,  a sequence of nonexpansive self-mappings on
a sequence of nonexpansive self-mappings on  such that
such that  and let
and let  be a sequence in
be a sequence in  for some
for some  . Then, for every
. Then, for every  and
and  the limit
the limit  exists.
exists.
Remark 2.4.
It can be known from Lemma 2.3 that if  is a nonempty bounded subset of
is a nonempty bounded subset of  , then for
, then for  there exists
there exists  such that
such that  for all
for all  .
.
Remark 2.5.
Using Lemma 2.3, we can define a mapping  as follows:
as follows:

for all  Such a
Such a  is called the
is called the  -mapping generated by
-mapping generated by  and
and  Since
Since  is nonexpansive mapping,
is nonexpansive mapping,  is also nonexpansive. Indeed, observe that for each
is also nonexpansive. Indeed, observe that for each  ,
,

If  is a bounded sequence in
is a bounded sequence in  , then we put
, then we put  . Hence, it is clear from Remark 2.4 that for
. Hence, it is clear from Remark 2.4 that for  there exists
there exists  such that for all
such that for all  This implies that
This implies that

Lemma 2.6 (see [8]).
Let  be a nonempty closed convex subset of a strictly convex Banach space
be a nonempty closed convex subset of a strictly convex Banach space  . Let
. Let  be a sequence of nonexpansive self-mappings on
be a sequence of nonexpansive self-mappings on  such that
such that  and let
and let  be a sequence in
be a sequence in  for some
for some  . Then,
. Then,  .
.
3. Strong Convergence Theorem
Theorem 3.1.
Let  be a closed convex subset of a Hilbert space
be a closed convex subset of a Hilbert space  and let
and let  and
and  be defined as (1.2). Assume that
be defined as (1.2). Assume that  for all
for all  and for some
and for some  and
and  for all
for all  and
and  . If
. If  then
then  generated by (1.3) converges strongly to
generated by (1.3) converges strongly to  .
.
Proof.
Firstly, we observe that  is convex by Lemma 2.2. Next, we show that
is convex by Lemma 2.2. Next, we show that  for all
for all  .
.
Indeed, for all  ,
,

Therefore,

That is  for all
for all  . Next we show that
. Next we show that  for all
for all  .
.
We prove this by induction. For  , we have
, we have  Assume that
Assume that  for all
for all  since
since  is the projection of
is the projection of  onto
onto  so
so

As  by the induction assumption, the last inequality holds, in particular, for all
by the induction assumption, the last inequality holds, in particular, for all  . This together with definition of
. This together with definition of  implies that
implies that  . Hence
. Hence  for all
for all  .
.
Notice that the definition of  implies
implies  . This together with the fact
. This together with the fact  further implies
further implies  for all
for all 
The fact  asserts that
asserts that  implies
implies

We now claim that  and
and  . Indeed,
. Indeed,

since  , we have
, we have

Thus

We now show  . Let
. Let  be any subsequence of
be any subsequence of  . Since
. Since  is a bounded subset of
is a bounded subset of  , there exists a subsequence
, there exists a subsequence  of
of  such that
such that

Since

it follows that  . By (3.1), we have
. By (3.1), we have

Hence

Thus,

Using (3.1) again, we obtain that

This imply that  . For the arbitrariness of
. For the arbitrariness of  , we have
, we have  and
and

Thus, by (3.4), (3.7) and (3.14), we have

Since  and
and  we have
we have

Thus, using (3.16), Lemma 2.1, and the boundedness of  , we get that
, we get that  . Since
. Since  and
and  , we have
, we have  where
where  . By the weak lower semicontinuity of the norm, we have
. By the weak lower semicontinuity of the norm, we have  for all
for all  . However, since
. However, since  , we must have
, we must have  for all
for all  . Hence
. Hence  and
and

That is,  converges to
converges to  .
.
This completes the proof.
References
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974, 44: 147–150. 10.1090/S0002-9939-1974-0336469-5
Deng L: On Chidume's open questions. Journal of Mathematical Analysis and Applications 1993,174(2):441–449. 10.1006/jmaa.1993.1129
Chidume CE: An iterative process for nonlinear Lipschitzian strongly accretive mappings in
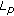 spaces. Journal of Mathematical Analysis and Applications 1990,151(2):453–461. 10.1016/0022-247X(90)90160-H
spaces. Journal of Mathematical Analysis and Applications 1990,151(2):453–461. 10.1016/0022-247X(90)90160-HRhoades BE: Comments on two fixed point iteration methods. Journal of Mathematical Analysis and Applications 1976,56(3):741–750. 10.1016/0022-247X(76)90038-X
Genel A, Lindenstrauss J: An example concerning fixed points. Israel Journal of Mathematics 1975,22(1):81–86. 10.1007/BF02757276
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. Journal of Mathematical Analysis and Applications 2003,279(2):372–379. 10.1016/S0022-247X(02)00458-4
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001,5(2):387–404.
Deng L, Liu Q: Iterative scheme for nonself generalized asymptotically quasi-nonexpansive mappings. Applied Mathematics and Computation 2008,205(1):317–324. 10.1016/j.amc.2008.08.027
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Martinez-Yanes C, Xu H-K: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2400–2411. 10.1016/j.na.2005.08.018
Acknowledgment
This work is supported by Grant KJ080725 of the Chongqing Municipal Education Commission.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, YA. Strong Convergence Theorems for Infinitely Nonexpansive Mappings in Hilbert Space. Fixed Point Theory Appl 2009, 962303 (2009). https://doi.org/10.1155/2009/962303
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/962303
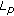 spaces. Journal of Mathematical Analysis and Applications 1990,151(2):453–461. 10.1016/0022-247X(90)90160-H
spaces. Journal of Mathematical Analysis and Applications 1990,151(2):453–461. 10.1016/0022-247X(90)90160-H