- Research Article
- Open access
- Published:
A Fixed Point Approach to the Stability of the Functional Equation 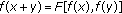
Fixed Point Theory and Applications volume 2009, Article number: 912046 (2009)
Abstract
By applying the fixed point method, we will prove the Hyers-Ulam-Rassias stability of the functional equation  under some additional assumptions on the function
under some additional assumptions on the function  and spaces involved.
and spaces involved.
1. Introduction
In 1940, Ulam [1] gave a wide ranging talk before the mathematics club of the University of Wisconsin in which he discussed a number of important unsolved problems. Among those was the question concerning the stability of group homomorphisms: "Let  be a group and let
be a group and let  be a metric group with the metric
be a metric group with the metric  . Given
. Given  , does there exist a
, does there exist a  such that if a function
such that if a function  satisfies the inequality
satisfies the inequality  for all
for all  , then there exists a homomorphism
, then there exists a homomorphism  with
with  for all
for all  ?''
?''
The case of approximately additive functions was solved by Hyers [2] under the assumption that  and
and  are Banach spaces. Indeed, he proved that each solution of the inequality
are Banach spaces. Indeed, he proved that each solution of the inequality  , for all
, for all  and
and  , can be approximated by an exact solution, say an additive function. Rassias [3] attempted to weaken the condition for the bound of the norm of the Cauchy difference as follows:
, can be approximated by an exact solution, say an additive function. Rassias [3] attempted to weaken the condition for the bound of the norm of the Cauchy difference as follows:

and derived Hyers' theorem for the stability of the additive mapping as a special case. Thus in [3], a proof of the generalized Hyers-Ulam stability for the linear mapping between Banach spaces was obtained. A particular case of Rassias' theorem regarding the Hyers-Ulam stability of the additive mapping was proved by Aoki (see [4]).
The stability concept that was introduced by Rassias' theorem provided a large influence to a number of mathematicians to develop the notion of what is known today with the term Hyers-Ulam-Rassias stability of the linear mapping. Since then, the stability of several functional equations has been extensively investigated by several mathematicians. The terminology Hyers-Ulam-Rassias stability originates from these historical backgrounds. The terminology can also be applied to the case of other functional equations. For more detailed definitions of such terminologies, we can refer to [5–10].
Solutions of the functional equation

were investigated in [11, Section 2.2]. The stability problem for a general equation of the form  was investigated by Cholewa [12] (see also [13]). Indeed, Cholewa proved the superstability of that equation under some additional assumptions on the functions and spaces involved.
was investigated by Cholewa [12] (see also [13]). Indeed, Cholewa proved the superstability of that equation under some additional assumptions on the functions and spaces involved.
In this paper, we will apply the fixed point method to prove the Hyers-Ulam-Rassias stability of the functional equation (1.2) for a class of functions of a vector space into a Banach space. To the best of authors' knowledge, no one has yet applied the fixed point method for studying the stability problems of (1.2). So, one of the aims of this paper is to apply the fixed point theory to this case.
Throughout this paper, let  denote either
denote either  or
or  . Let
. Let  and
and  be a vector space over
be a vector space over  and a Banach space over
and a Banach space over  , respectively.
, respectively.
2. Preliminaries
Let  be a set. A function
be a set. A function  is called a generalized metric on
is called a generalized metric on  if and only if
if and only if  satisfies
satisfies
() if and only if
if and only if  ;
;
() for all
for all  ;
;
() for all
for all  .
.
Note that the only substantial difference of the generalized metric from the metric is that the range of generalized metric includes the infinity. We now introduce one of fundamental results of fixed point theory. For the proof, refer to [14]. For an extensive theory of fixed point theorems and other nonlinear methods the reader is referred to the book of Hyers et al. [15].
Theorem 2.1.
Let  be a generalized complete metric space. Assume that
be a generalized complete metric space. Assume that  is a strictly contractive operator with the Lipschitz constant
is a strictly contractive operator with the Lipschitz constant  . If there exists a nonnegative integer
. If there exists a nonnegative integer  such that
such that  for some
for some  , then the followings are true:
, then the followings are true:
(a)the sequence  converges to a fixed point
converges to a fixed point  of
of  ;
;
(b) is the unique fixed point of
is the unique fixed point of  in
in

(c)if  , then
, then

Recently, Cădariu and Radu [16] applied the fixed point method to the investigation of the Cauchy additive functional equation [17, 18]. Using such a clever idea, they could present a short, simple proof for the Hyers-Ulam-Rassias stability of Cauchy and Jensen functional equations.
We remark that Isac and Rassias [19] were the first mathematicians who apply the Hyers-Ulam-Rassias stability approach for the proof of new fixed point theorems.
3. Main Results
In this section, by using an idea of Cădariu and Radu (see [16, 17]), we will prove the Hyers-Ulam-Rassias stability of the functional equation  under the assumption that
under the assumption that  is a bounded linear transformation.
is a bounded linear transformation.
Theorem 3.1.
Let  and
and  be a vector space over
be a vector space over  and a Banach space over
and a Banach space over  , respectively, and let
, respectively, and let  be a Banach space over
be a Banach space over  . Assume that
. Assume that  is a bounded linear transformation, whose norm is denoted by
is a bounded linear transformation, whose norm is denoted by  , satisfying
, satisfying

for all  and that there exists a real number
and that there exists a real number  with
with

for all  . Moreover, assume that
. Moreover, assume that  is a given function satisfying
is a given function satisfying

for all  . If
. If  and a function
and a function  satisfies the inequality
satisfies the inequality

for any  , then there exists a unique solution
, then there exists a unique solution  of (1.2) such that
of (1.2) such that

for all  .
.
Proof.
First, we denote by  the set of all functions
the set of all functions  and by
and by  the generalized metric on
the generalized metric on  defined as
defined as

Then, as in the proof of [20, Theorem 3.1], we can show that  is a generalized complete metric space. Now, let us define an operator
is a generalized complete metric space. Now, let us define an operator  by
by

for every  .
.
We assert that  is strictly contractive on
is strictly contractive on  . Given
. Given  , let
, let  be an arbitrary constant with
be an arbitrary constant with  , that is,
, that is,

for each  . By (3.2), (3.3), (3.7), and (3.8), we have
. By (3.2), (3.3), (3.7), and (3.8), we have

for all  , that is, in view of (3.6),
, that is, in view of (3.6),  for any
for any  , where
, where  is the Lipschitz constant with
is the Lipschitz constant with  . Thus,
. Thus,  is strictly contractive.
is strictly contractive.
We now verify that  . If we substitute
. If we substitute  for
for  and
and  in (3.4), then it follows from (3.3) and (3.7) that
in (3.4), then it follows from (3.3) and (3.7) that

for every  , that is,
, that is,  .
.
Taking  in Theorem 2.1, (a) implies that there exists a function
in Theorem 2.1, (a) implies that there exists a function  , which is a fixed point of
, which is a fixed point of  , such that
, such that

Due to Theorem 2.1(c), we get

which implies the validity of (3.5). According to Theorem 2.1(b),  is the unique fixed point of
is the unique fixed point of  with
with  .
.
We now assert that

for all  and
and  . Indeed, it follows from (3.1), (3.2), (3.3), (3.4), and (3.7) that
. Indeed, it follows from (3.1), (3.2), (3.3), (3.4), and (3.7) that

for any  . We assume that (3.13) is true for some
. We assume that (3.13) is true for some  . Then, it follows from (3.1), (3.2), (3.3), (3.7), and (3.13) that
. Then, it follows from (3.1), (3.2), (3.3), (3.7), and (3.13) that

which proves the validity of (3.13) for all  .
.
Finally, we prove that  for any
for any  . Since
. Since  is continuous as a bounded linear transformation, it follows from (3.11) and (3.13) that
is continuous as a bounded linear transformation, it follows from (3.11) and (3.13) that

which ends our proof.
Obviously, for nonnegative constants  and
and  ,
,  satisfies the conditon (3.3).
satisfies the conditon (3.3).
Corollary 3.2.
Let  and
and  be a vector space over
be a vector space over  and a Banach space over
and a Banach space over  , respectively, and let
, respectively, and let  be a Banach space over
be a Banach space over  . Assume that
. Assume that  is a bounded linear transformation, whose norm is denoted by
is a bounded linear transformation, whose norm is denoted by  , satisfying the condition (3.1) and that there exists a real number
, satisfying the condition (3.1) and that there exists a real number  satisfying the condition (3.2). If
satisfying the condition (3.2). If  and a function
and a function  satisfies the inequality
satisfies the inequality

for all  and for some nonnegative real constants
and for some nonnegative real constants  and
and  , then there exists a unique solution
, then there exists a unique solution  of (1.2) such that
of (1.2) such that

for all  .
.
4. An Example
Assume that  and consider the Banach spaces
and consider the Banach spaces  and
and  , where we define
, where we define  for all
for all  . Let
. Let  and
and  be fixed complex numbers with
be fixed complex numbers with  and let
and let  be a linear transformation defined by
be a linear transformation defined by

Then it is easy to show that  satisfies the condition (3.1).
satisfies the condition (3.1).
If  and
and  are complex numbers satisfying
are complex numbers satisfying  , then
, then

Thus, we get

which implies the boundedness of the linear transformation  .
.
On the other hand, we obtain

for any  ; that is, we can choose
; that is, we can choose  for the value of
for the value of  and then we have
and then we have

If a function  satisfies the inequality
satisfies the inequality

for all  and for some
and for some  , then our Corollary 3.2 (with
, then our Corollary 3.2 (with  and
and  ) implies that there exists a unique function
) implies that there exists a unique function  such that
such that

for all  and
and

for any  .
.
References
Ulam SM: A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, no. 8. Interscience, New York, NY, USA; 1960.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences 1941, 27: 222–224. 10.1073/pnas.27.4.222
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Forti GL: Hyers-Ulam stability of functional equations in several variables. Aequationes Mathematicae 1995,50(1–2):143–190. 10.1007/BF01831117
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications. Birkhäuser, Boston, Mass, USA; 1998.
Hyers DH, Rassias ThM: Approximate homomorphisms. Aequationes Mathematicae 1992,44(2–3):125–153. 10.1007/BF01830975
Jung S-M: Hyers-Ulam-Rassias stability of functional equations. Dynamic Systems and Applications 1997,6(4):541–565.
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001.
Rassias ThM: On the stability of functional equations and a problem of Ulam. Acta Applicandae Mathematicae 2000,62(1):23–130. 10.1023/A:1006499223572
Aczél J: Lectures on Functional Equations and Their Applications, Mathematics in Science and Engineering. Volume 19. Academic Press, New York, NY, USA; 1966.
Cholewa PW: The stability problem for a generalized Cauchy type functional equation. Revue Roumaine de Mathématiques Pures et Appliquées 1984,29(6):457–460.
Forti GL: An existence and stability theorem for a class of functional equations. Stochastica 1980,4(1):23–30. 10.1080/17442508008833155
Margolis B, Diaz J: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74: 305–309. 10.1090/S0002-9904-1968-11933-0
Hyers DH, Isac G, Rassias ThM: Topics in Nonlinear Analysis & Applications. World Scientific, River Edge, NJ, USA; 1997.
Cădariu L, Radu V: On the stability of the Cauchy functional equation: a fixed point approach. Grazer Mathematische Berichte 2004, 346: 43–52.
Cădariu L, Radu V: Fixed points and the stability of Jensen's functional equation. Journal of Inequalities in Pure and Applied Mathematics 2003.,4(1, article 4):
Radu V: The fixed point alternative and the stability of functional equations. Fixed Point Theory 2003,4(1):91–96.
Isac G, Rassias ThM: Stability of -additive mappings: applications to nonlinear analysis. International Journal of Mathematics and Mathematical Sciences 1996,19(2):219–228. 10.1155/S0161171296000324
Jung S-M, Lee Z-H: A fixed point approach to the stability of quadratic functional equation with involution. Fixed Point Theory and Applications 2008, 2008:-11.
Acknowledgments
The authors would like to express their cordial thanks to the referees for their useful comments which have improved the first version of this paper. This work was supported by the National Research Foundation of Korea Grant funded by the Korean Government (no. 2009-0071206).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jung, SM., Min, S. A Fixed Point Approach to the Stability of the Functional Equation 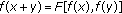 .
Fixed Point Theory Appl 2009, 912046 (2009). https://doi.org/10.1155/2009/912046
.
Fixed Point Theory Appl 2009, 912046 (2009). https://doi.org/10.1155/2009/912046
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/912046