- Research Article
- Open access
- Published:
Common Fixed Points of Generalized Contractive Hybrid Pairs in Symmetric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 869407 (2009)
Abstract
Several fixed point theorems for hybrid pairs of single-valued and multivalued occasionally weakly compatible maps satisfying generalized contractive conditions are established in a symmetric space.
1. Introduction and Preliminaries
In 1968, Kannan [1] proved a fixed point theorem for a map satisfying a contractive condition that did not require continuity at each point. This paper was a genesis for a multitude of fixed point papers over the next two decades. Sessa [2] coined the term weakly commuting maps. Jungck [3] generalized the notion of weak commutativity by introducing compatible maps and then weakly compatible maps [4]. Al-Thagafi and Shahzad [5] gave a definition which is proper generalization of nontrivial weakly compatible maps which have coincidence points. Jungck and Rhoades [6] studied fixed point results for occasionally weakly compatible (owc) maps. Recently, Zhang [7] obtained common fixed point theorems for some new generalized contractive type mappings. Abbas and Rhoades [8] obtained common fixed point theorems for hybrid pairs of single-valued and multivalued owc maps defined on a symmetric space (see also [9]). For other related fixed point results in symmetric spaces and their applications, we refer to [10–15]. The aim of this paper is to obtain fixed point theorems involving hybrid pairs of single-valued and multivalued owc maps satisfying a generalized contractive condition in the frame work of a symmetric space.
Definition 1.1.
A symmetric on a set  is a mapping
is a mapping  such that
such that

A set  together with a symmetric
together with a symmetric  is called a symmetric space.
is called a symmetric space.
We will use the following notations, throughout this paper, where  is a symmetric space,
is a symmetric space,  and
and  , and
, and  is the class of all nonempty bounded subsets of
is the class of all nonempty bounded subsets of  The diameter of
The diameter of  is denoted and defined by
is denoted and defined by

Clearly,  For
For  and
and  we write
we write  and
and  respectively. We appeal to the fact that
respectively. We appeal to the fact that  if and only if
if and only if  for
for 
Recall that  is called a coincidence point (resp., common fixed point) of
is called a coincidence point (resp., common fixed point) of  and
and  if
if  (resp.,
(resp.,  ).
).
Definition 1.2.
Maps  and
and  are said to becompatible if
are said to becompatible if  for each
for each  and
and  whenever
whenever  is a sequence in
is a sequence in  such that
such that  (
( ) and
) and  for some
for some  [21].
[21].
Definition 1.3.
Maps  and
and  are said to be weakly compatible if
are said to be weakly compatible if  whenever
whenever 
Definition 1.4.
Maps  and
and  are said to be owc if and only if there exists some point
are said to be owc if and only if there exists some point  in
in  such that
such that  and
and 
Example 1.5.
Consider  with usual metric.
with usual metric.
-
(a)
Define
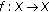 and
and 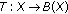 as:
as: 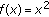 and
and 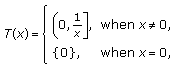 (1.3)
(1.3)
then  and
and  are weakly compatible.
are weakly compatible.
-
(b)
Define
 by
by 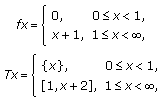 (1.4)
(1.4)
It can be easily verified that  is coincidence point of
is coincidence point of  and
and  but
but  and
and  are not weakly compatible there, as
are not weakly compatible there, as  . Hence
. Hence  and
and  are not compatible. However, the pair
are not compatible. However, the pair  is occasionally weakly compatible, since the pair
is occasionally weakly compatible, since the pair  is weakly compatible at
is weakly compatible at 
Assume that  satisfies the following.
satisfies the following.
(i) and
and  for each
for each  .
.
(ii) is nondecreasing on
is nondecreasing on 
Define,  satisfies
satisfies  above
above
Let  satisfy the following.
satisfy the following.
(iii) for each
for each  .
.
(iv) is nondecreasing on
is nondecreasing on 
Define,  satisfies
satisfies  above
above
For some examples of mappings  which satisfy
which satisfy  we refer to [7].
we refer to [7].
2. Common Fixed Point Theorems
In the sequel we shall consider,  which is defined on
which is defined on  where
where  stands for a real number to the left of
stands for a real number to the left of  and assume that the mapping
and assume that the mapping  satisfies
satisfies  above.
above.
Theorem 2.1.
Let  be self maps of a symmetric space
be self maps of a symmetric space  , and let
, and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  If
If

for each  for which
for which  where
where

then  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By hypothesis there exist points  in
in  such that
such that  , and
, and  . Also,
. Also,  Therefore by (2.2) we have
Therefore by (2.2) we have

Now we claim that  . For, otherwise, by (2.1),
. For, otherwise, by (2.1),

a contradiction and hence  Obviously,
Obviously,  Thus (2.2) gives
Thus (2.2) gives

Next we claim that  If not, then (2.1) implies
If not, then (2.1) implies

which is a contradiction and the claim follows. Similarly, we obtain  Thus
Thus  , and
, and  have a common fixed point. Uniqueness follows from (2.1).
have a common fixed point. Uniqueness follows from (2.1).
Corollary 2.2.
Let  be self maps of a symmetric space
be self maps of a symmetric space  and let
and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  If
If

for each  for which
for which  where
where

and  , then
, then  have a unique common fixed point.
have a unique common fixed point.
Proof.
Since (2.7) is a special case of (2.1), the result follows from Theorem 2.1.
Corollary 2.3.
Let  be self maps of a symmetric space
be self maps of a symmetric space  and let
and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  . If
. If

for each  for which
for which  where
where

where  and
and  Then
Then  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Note that

So, (2.9) is a special case of (2.1) and hence the result follows from Theorem 2.1.
Corollary 2.4.
Let  be a self map on a symmetric space
be a self map on a symmetric space  and let
and let  be a map from
be a map from  into
into  such that
such that  and
and  are
are  . If
. If

for each  for which
for which  where
where

Then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Condition (2.12) is a special case of condition (2.1) with  and
and  Therefore the result follows from Theorem 2.1.
Therefore the result follows from Theorem 2.1.
Theorem 2.5.
Let  be self maps of a symmetric space
be self maps of a symmetric space  and let
and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  If
If

for each  for which
for which  ,
,

where  , and
, and  , then
, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By hypothesis there exist points  in
in  such that
such that  and
and  Therefore by (2.15) we have
Therefore by (2.15) we have

Now we show that  . Suppose not. Then condition (2.14) implies that
. Suppose not. Then condition (2.14) implies that

which is a contradiction and hence  Note that,
Note that,  Thus (2.15) gives
Thus (2.15) gives

Now we claim that  If not, then condition (2.14) implies that
If not, then condition (2.14) implies that

which is a contradiction, and hence the claim follows. Similarly, we obtain  Thus
Thus  , and
, and  have a common fixed point. Uniqueness follows easily from (2.14).
have a common fixed point. Uniqueness follows easily from (2.14).
Define  such that
such that
) is nondecreasing in the 4th and 5th variables,
is nondecreasing in the 4th and 5th variables,
) if  is such that
is such that

then  .
.
Theorem 2.6.
Let  be self maps of a symmetric space
be self maps of a symmetric space  and let
and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  . If
. If

for all  for which
for which  where
where  then
then  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By hypothesis there exist points  in
in  such that
such that  , and
, and  Also,
Also,  First we show that
First we show that  . Suppose not. Then condition (2.21) implies that
. Suppose not. Then condition (2.21) implies that

which, from  implies that
implies that  this further implies that,
this further implies that,  a contradiction. Hence the claim follows. Also,
a contradiction. Hence the claim follows. Also,  Next we claim that
Next we claim that  If not, then condition (2.21) implies that
If not, then condition (2.21) implies that

which, from  and
and  implies that
implies that  this further implies that
this further implies that  Hence the claim follows. Similarly, it can be shown that
Hence the claim follows. Similarly, it can be shown that  which proves that
which proves that  is a common fixed point of
is a common fixed point of  , and
, and  . Uniqueness follows from (2.21) and (
. Uniqueness follows from (2.21) and ( ).
).
A control function  is a continuous monotonically increasing function that satisfies
is a continuous monotonically increasing function that satisfies  and,
and,  if and only if
if and only if 
Let  be such that
be such that  for each
for each 
Theorem 2.7.
Let  be self maps of symmetric space
be self maps of symmetric space  and let
and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  If for a control function
If for a control function  one has
one has

for each  for which right-hand side of (2.24) is not equal to zero
for which right-hand side of (2.24) is not equal to zero where
where

then  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By hypothesis there exist points  in
in  such that
such that  , and
, and  Also, using the triangle inequality, we obtain
Also, using the triangle inequality, we obtain  Therefore by (2.25) we have
Therefore by (2.25) we have

Now we show that  . Suppose not. Then condition (2.24) implies that
. Suppose not. Then condition (2.24) implies that

which is a contradiction. Therefore  which further implies that,
which further implies that,  Hence the claim follows. Again,
Hence the claim follows. Again,  Therefore by (2.25) we have
Therefore by (2.25) we have

Next we claim that  If not, then condition (2.24) implies
If not, then condition (2.24) implies

which is a contradiction. Therefore  which further implies that
which further implies that  Hence the claim follows. Similarly, it can be shown that
Hence the claim follows. Similarly, it can be shown that  which proves the result.
which proves the result.
Set 
 is continuous and nondecreasing mapping with
is continuous and nondecreasing mapping with  if and only if
if and only if 
The following theorem generalizes [16, Theorem  ].
].
Theorem 2.8.
Let  be self maps of a symmetric space
be self maps of a symmetric space  , and let
, and let  be maps from
be maps from  into
into  such that the pairs
such that the pairs  and
and  are
are  If
If

for all  , for which right-hand side of (2.30) is not equal to zero
, for which right-hand side of (2.30) is not equal to zero where
where  then
then  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Proof.
By hypothesis there exist points  in
in  such that
such that  , and
, and  Also, using the triangle inequality, we obtain,
Also, using the triangle inequality, we obtain,  Now we claim that
Now we claim that  . For, otherwise, by (2.30),
. For, otherwise, by (2.30),

which is a contradiction. Therefore  Hence the claim follows. Again,
Hence the claim follows. Again,  Now we claim that
Now we claim that  If not, then condition (2.30) implies that
If not, then condition (2.30) implies that

which is a contradiction, and hence the claim follows. Similarly, it can be shown that  which, proves that
which, proves that  is a common fixed point of
is a common fixed point of  , and
, and  . Uniqueness follows easily from (2.30).
. Uniqueness follows easily from (2.30).
Example 2.9.
Let  Define
Define  by
by

Note that  is symmetric but not a metric on
is symmetric but not a metric on  .
.
Define  by
by

and  as follows:
as follows:

Clearly,  but
but  and
and  but
but  they show that
they show that  is not weakly compatible. On the other hand,
is not weakly compatible. On the other hand,  gives that
gives that  Hence
Hence  is occasionally weakly compatible. Note that
is occasionally weakly compatible. Note that  ,
,  ,
,  , and
, and  they imply that
they imply that  is not weakly compatible
is not weakly compatible Now
Now  gives that
gives that  . Hence
. Hence  is occasionally weakly compatible. As
is occasionally weakly compatible. As  and
and  so
so  is the unique common fixed point of
is the unique common fixed point of  , and
, and 
Remark 2.10 s.
Weakly compatible maps are occasionally weakly compatible but converse is not true in general. The class of symmetric spaces is more general than that of metric spaces. Therefore the following results can be viewed as special cases of our results:
(a)([17, Theorem  ] and [18, Theorem
] and [18, Theorem  ]) are special cases of Theorem 2.7.
]) are special cases of Theorem 2.7.
(b)[19, Theorem  ], [20, Theorem
], [20, Theorem  ], [21, Theorem
], [21, Theorem  ], and [22, Theorem
], and [22, Theorem  ] are special cases of Corollary 2.2. Moreover, [23, Theorem
] are special cases of Corollary 2.2. Moreover, [23, Theorem  ] and [24, Theorem
] and [24, Theorem  ] also become special cases of Corollary 2.2.
] also become special cases of Corollary 2.2.
-
(c)
([25, Theorem
 ]) is a special case of Theorem 2.1. Theorem 2.1 also generalizes ([26, Theorem
]) is a special case of Theorem 2.1. Theorem 2.1 also generalizes ([26, Theorem  ]) and ( [27, Theorems
]) and ( [27, Theorems  and
and  ]).
]).
(d)[28, Theorem  ] becomes special case of Corollary 2.4.
] becomes special case of Corollary 2.4.
References
Kannan R: Some results on fixed points. Bulletin of the Calcutta Mathematical Society 1968, 60: 71–76.
Sessa S: On a weak commutativity condition of mappings in fixed point considerations. Publications de l'Institut Mathématique. Nouvelle Série 1982, 32(46): 149–153.
Jungck G: Compatible mappings and common fixed points. International Journal of Mathematics and Mathematical Sciences 1986,9(4):771–779. 10.1155/S0161171286000935
Jungck G: Common fixed points for noncontinuous nonself maps on nonmetric spaces. Far East Journal of Mathematical Sciences 1996,4(2):199–215.
Al-Thagafi MA, Shahzad N: Generalized -nonexpansive selfmaps and invariant approximations. Acta Mathematica Sinica 2008,24(5):867–876. 10.1007/s10114-007-5598-x
Jungck G, Rhoades BE: Fixed point theorems for occasionally weakly compatible mappings. Fixed Point Theory 2006,7(2):287–296.
Zhang X: Common fixed point theorems for some new generalized contractive type mappings. Journal of Mathematical Analysis and Applications 2007,333(2):780–786. 10.1016/j.jmaa.2006.11.028
Abbas M, Rhoades BE: Common fixed point theorems for hybrid pairs of occasionally weakly compatible mappings defined on symmetric spaces. Panamerican Mathematical Journal 2008,18(1):55–62.
Abbas M, Rhoades BE: Common fixed point theorems for occasionally weakly compatible mappings satisfying a generalized contractive condition. Mathematical Communications 2008,13(2):295–301.
Aliouche A: A common fixed point theorem for weakly compatible mappings in symmetric spaces satisfying a contractive condition of integral type. Journal of Mathematical Analysis and Applications 2006,322(2):796–802. 10.1016/j.jmaa.2005.09.068
Chandra H, Bhatt A: Some fixed point theorems for set valued maps in symmetric spaces. International Journal of Mathematical Analysis 2009,3(17):839–846.
Cho S-H, Lee G-Y, Bae J-S: On coincidence and fixed-point theorems in symmetric spaces. Fixed Point Theory and Applications 2008, 2008:-9.
Hicks TL, Rhoades BE: Fixed point theory in symmetric spaces with applications to probabilistic spaces. Nonlinear Analysis: Theory, Methods & Applications 1999,36(3):331–344. 10.1016/S0362-546X(98)00002-9
Imdad M, Ali J: Common fixed point theorems in symmetric spaces employing a new implicit function and common property (E.A). Bulletin of the Belgian Mathematical Society. Simon Stevin 2009, 16: 421–433.
Pathak HK, Tiwari R, Khan MS: A common fixed point theorem satisfying integral type implicit relations. Applied Mathematics E-Notes 2007, 7: 222–228.
Beg I, Abbas M: Coincidence point and invariant approximation for mappings satisfying generalized weak contractive condition. Fixed Point Theory and Applications 2006, 2006:-7.
Chang TH: Common fixed point theorems for multivalued mappings. Mathematica Japonica 1995,41(2):311–320.
Shrivastava PK, Bawa NPS, Nigam SK: Fixed point theorems for hybrid contractions. Varāhmihir Journal of Mathematical Sciences 2002,2(2):275–281.
Azam A, Beg I: Coincidence points of compatible multivalued mappings. Demonstratio Mathematica 1996,29(1):17–22.
Kamran T: Common coincidence points of R -weakly commuting maps. International Journal of Mathematics and Mathematical Sciences 2001,26(3):179–182. 10.1155/S0161171201005245
Jungck G, Rhoades BE: Fixed points for set valued functions without continuity. Indian Journal of Pure and Applied Mathematics 1998,29(3):227–238.
Hadžić O: Common fixed point theorems for single-valued and multivalued mappings. Review of Research. Faculty of Science. Mathematics Series 1988,18(2):145–151.
Kaneko H, Sessa S: Fixed point theorems for compatible multi-valued and single-valued mappings. International Journal of Mathematics and Mathematical Sciences 1989,12(2):257–262. 10.1155/S0161171289000293
Kaneko H: A common fixed point of weakly commuting multi-valued mappings. Mathematica Japonica 1988,33(5):741–744.
Fisher B: Common fixed points for set-valued mappings. Indian Journal of Mathematics 1983,25(3):265–270.
Sessa S, Fisher B: On common fixed points of weakly commuting mappings and set-valued mappings. International Journal of Mathematics and Mathematical Sciences 1986,9(2):323–329. 10.1155/S0161171286000406
Fisher B: Common fixed point theorem for commutative mappings and set valued mappings. Journal of University of Kuwait 1984, 11: 15–21.
Dhage BC: Common fixed point theorems for coincidentally commuting pairs of nonself mappings in metrically convex metric spaces. Analele Ştiinţifice ale Universităţii Al. I. Cuza din Iaşi. Serie Nouă. Matematică 2003,49(1):45–60.
Acknowledgments
The authors are thankful to the referees for their critical remarks to improve this paper. The second author gratefully acknowledges the support provided by King Fahad University of Petroleum and Minerals during this research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abbas, M., Khan, A.R. Common Fixed Points of Generalized Contractive Hybrid Pairs in Symmetric Spaces. Fixed Point Theory Appl 2009, 869407 (2009). https://doi.org/10.1155/2009/869407
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/869407
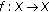 and
and 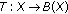 as:
as: 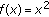 and
and 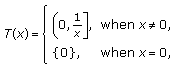
 by
by 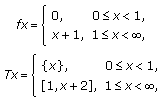
 ]) is a special case of Theorem 2.1. Theorem 2.1 also generalizes ([
]) is a special case of Theorem 2.1. Theorem 2.1 also generalizes ([ ]) and ( [
]) and ( [ and
and  ]).
]).