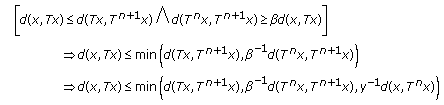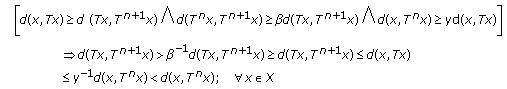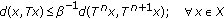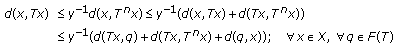- Research Article
- Open access
- Published:
Some Combined Relations between Contractive Mappings, Kannan Mappings, Reasonable Expansive Mappings, and 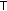 -Stability
-Stability
Fixed Point Theory and Applications volume 2009, Article number: 815637 (2009)
Abstract
In recent literature concerning fixed point theory for self-mappings  in metric spaces
in metric spaces  , there are some new concepts which can be mutually related so that the inherent properties of each one might be combined for such self-mappings. Self-mappings
, there are some new concepts which can be mutually related so that the inherent properties of each one might be combined for such self-mappings. Self-mappings  can be referred to, for instance, as Kannan-mappings, reasonable expansive mappings, and Picard
can be referred to, for instance, as Kannan-mappings, reasonable expansive mappings, and Picard  -stable mappings. Some relations between such concepts subject either to sufficient, necessary, or necessary and sufficient conditions are obtained so that in certain self-mappings can exhibit combined properties being inherent to each of its various characterizations.
-stable mappings. Some relations between such concepts subject either to sufficient, necessary, or necessary and sufficient conditions are obtained so that in certain self-mappings can exhibit combined properties being inherent to each of its various characterizations.
1. Introduction
As it is wellknown fixed point theory and related techniques are of increasing interest for solving a wide class of mathematical problems where convergence of a trajectory or sequence to some equilibrium set is essential, (see, e.g., [1–7]). Some of the specific topics recently covered in the field of fixed point theory are, for instance as follows.
(1)The properties of the so-called  -times reasonably expansive mapping are investigated in [1] in complete metric spaces
-times reasonably expansive mapping are investigated in [1] in complete metric spaces  as those fulfilling the property that
as those fulfilling the property that  for some real constant
for some real constant  . The conditions for the existence of fixed points in such mappings are investigated.
. The conditions for the existence of fixed points in such mappings are investigated.
(2)Strong convergence of the wellknown Halpern's iteration and variants is investigated in [2, 8] and several the references therein.
(3)Fixed point techniques have been recently used in [4] for the investigation of global stability of a wide class of time-delay dynamic systems which are modeled by functional equations.
(4)Generalized contractive mappings have been investigated in [5] and references therein, weakly contractive and nonexpansive mappings are investigated in [6] and references therein.
(5)The existence of fixed points of Liptchitzian semigroups has been investigated, for instance, in [3].
(6)Picard's  -stability is discussed in [9] related to the convergence of perturbed iterations to the same fixed points as the nominal iteration under certain conditions in a complete metric space.
-stability is discussed in [9] related to the convergence of perturbed iterations to the same fixed points as the nominal iteration under certain conditions in a complete metric space.
(7)The so-called Kannan mappings in [10] are recently investigated in [11, 12] and references therein.
Let  be a metric space. Consider a self-mapping
be a metric space. Consider a self-mapping  . The basic concepts used through the manuscript are the subsequent ones:
. The basic concepts used through the manuscript are the subsequent ones:
(1) is
is  -contractive, following the contraction Banach's principle, if there exists a real constant
-contractive, following the contraction Banach's principle, if there exists a real constant  such that
such that

(2) is
is  -Kannan, [10–12], if there exists a real constant
-Kannan, [10–12], if there exists a real constant  such that
such that

(3) is
is  (
( )-times reasonable expansive self-mapping if there exists a real constant
)-times reasonable expansive self-mapping if there exists a real constant  such that
such that  ;
;  ,
,  , [1],
, [1],
(4)Picard's  -stability means that if
-stability means that if  is a complete metric space and Picard's iteration
is a complete metric space and Picard's iteration  satisfies
satisfies  as
as  for
for  then
then  , that is, q is a fixed point of
, that is, q is a fixed point of  , [9]. It is proven in [9] that, if the self-mapping
, [9]. It is proven in [9] that, if the self-mapping  satisfies a property, referred to through this manuscript as the
satisfies a property, referred to through this manuscript as the  property for some real constants
property for some real constants  and
and  (see Definition 1.2 in what follows), then Picard's iteration is
(see Definition 1.2 in what follows), then Picard's iteration is  -stable if
-stable if  .
.
The following result is direct.
Proposition 1.1.
If a self-mapping  is
is  -contractive, then it is also
-contractive, then it is also  -contractive;
-contractive;  .
.
If a self-mapping  is
is  -Kannan, then it is also
-Kannan, then it is also  -Kannan;
-Kannan;  .
.
The so- called the  -property is defined as follows.
-property is defined as follows.
Definition 1.2.
A self-mapping  with
with  possesses the
possesses the  -property for some real constants
-property for some real constants  and
and  if
if  ;
;  ,
,  .
.
The above property has been introduced in [9] to discuss the  -stability of Picard's iteration. If the
-stability of Picard's iteration. If the  -property is fulfilled in a complete metric space and, furthermore,
-property is fulfilled in a complete metric space and, furthermore,  , then Picard's iteration
, then Picard's iteration  is
is  -stable defined as
-stable defined as  as
as  as
as  . The main results obtained in this paper rely on the following features.
. The main results obtained in this paper rely on the following features.
(1)In fact  -contractive mappings
-contractive mappings  are
are  -Kannan self-mappings and vice-versa under certain mutual constraints between the constants
-Kannan self-mappings and vice-versa under certain mutual constraints between the constants  and
and  , [10–12]. A necessary and sufficient condition for both properties to hold is given. Some of such constraints are obtained in the manuscript. The existence of fixed points and their potential uniqueness is discussed accordingly under completeness of the metric space, [1–4, 8–10, 13].
, [10–12]. A necessary and sufficient condition for both properties to hold is given. Some of such constraints are obtained in the manuscript. The existence of fixed points and their potential uniqueness is discussed accordingly under completeness of the metric space, [1–4, 8–10, 13].
(2)If  is
is  (
( )-times reasonable expansive self-mapping then it cannot be contractive as expected but it is
)-times reasonable expansive self-mapping then it cannot be contractive as expected but it is  -Kannan under certain constraints. The converse is also true under certain constraints. Some of such constraints referred to are obtained explicitly in the manuscript. The existence of fixed points is also discussed for two types of
-Kannan under certain constraints. The converse is also true under certain constraints. Some of such constraints referred to are obtained explicitly in the manuscript. The existence of fixed points is also discussed for two types of  (
( )-times reasonable expansive self-mappings proposed in [1].
)-times reasonable expansive self-mappings proposed in [1].
(3)The  -property guaranteeing Picard's
-property guaranteeing Picard's  -stability of iterative schemes, under the added condition
-stability of iterative schemes, under the added condition  , is compatible with both contractive self-mappings and
, is compatible with both contractive self-mappings and  -Kannan ones under certain constraints. A sufficient condition that as self-mapping possessing the
-Kannan ones under certain constraints. A sufficient condition that as self-mapping possessing the  -property is
-property is  -Kannan is also given. It may be also fulfilled by
-Kannan is also given. It may be also fulfilled by  (
( )-times reasonable expansive self-mappings.
)-times reasonable expansive self-mappings.
1.1. Notation
Assume that  and
and  are the sets of integer and real numbers,
are the sets of integer and real numbers,  ,
,  ,
,  ,
,  .
.
If  is a self mapping in a metric space
is a self mapping in a metric space  , then
, then  denotes the set of fixed points of
denotes the set of fixed points of  .
.
2. Combined Compatible Relations of  -Contractive Mappings,
-Contractive Mappings,  -Kannan Mappings, and the
-Kannan Mappings, and the  -Property
-Property
It is of interest to establish when a  -contractive mapping is also
-contractive mapping is also  -Kannan and viceversa.
-Kannan and viceversa.
Theorem 2.1.
The following properties hold:
(i)if  is
is  -contractive with
-contractive with  then it is
then it is  -Kannan with
-Kannan with  ,
,
(ii) is
is  -contractive and
-contractive and  -Kannan if and only if
-Kannan if and only if

(iii)if  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  and
and  then the inequality
then the inequality

cannot hold for all  , y in
, y in  ,
,
(iv)if  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  , and
, and then the inequalities:
then the inequalities:

are feasible for all  , y in
, y in  .
.
Proof.
-
(i)
Since
 is
is  -contractive, then
-contractive, then  (2.4)
(2.4)
from the triangle inequality property of the distance in metric spaces. Since  , then
, then

so that  is
is  -Kannan with
-Kannan with  provided that
provided that  . As a result, if
. As a result, if  is
is  -contractive with
-contractive with  , then it is also
, then it is also  -Kannan.
-Kannan.
-
(ii)
It is direct if
 is
is  -contractive and
-contractive and  -Kannan with
-Kannan with 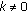 and
and  . For
. For  , the result holds trivially.
, the result holds trivially. -
(iii)
Proceed by contradiction. Assume that the inequality holds for
 with
with  where
where  is the (empty or nonempty) set of fixed points of
is the (empty or nonempty) set of fixed points of  . Since
. Since  , the inequality leads to
, the inequality leads to  . This implies that
. This implies that  since
since 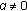 . However,
. However,  ;
; 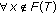 , what is a contradiction. Therefore, the inequality cannot cold in X.
, what is a contradiction. Therefore, the inequality cannot cold in X. -
(iv)
The first inequality can potentially hold even for the set of fixed points. Furthermore, one gets from the triangle inequality for the distance
 :
: 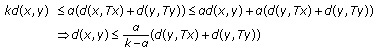 (2.6)
(2.6)
for all  . Also, by using
. Also, by using  , one gets
, one gets  . As a result, the second inequality follows by combining both partial results. The third inequality follows from the second one and Property (i). Property (iv) has been proven.
. As a result, the second inequality follows by combining both partial results. The third inequality follows from the second one and Property (i). Property (iv) has been proven.
Theorem 2.1(ii) leads to the subsequent result.
Corollary 2.2.
If  is
is  -contractive and
-contractive and  -Kannan, then
-Kannan, then

Proof.
One gets from Theorem 2.1(ii) for  that
that  ;
;  and
and  ;
;  . Both inequalities together yield the result.
. Both inequalities together yield the result.
The following two results follows directly from Theorem 2.1(iii) for  .
.
Corollary 2.3.
If  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  , then the inequality
, then the inequality  cannot hold
cannot hold  .
.
Corollary 2.4.
If  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  , then the inequality
, then the inequality  cannot hold for
cannot hold for .
.
The following three results follows directly from Theorem 2.1(iv) for  .
.
Corollary 2.5.
If  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  , then the inequality
, then the inequality  is feasible
is feasible  .
.
Proof.
The proof follows since

is feasible from the first feasible inequality in Theorem 2.1(ii)  and
and  .
.
Corollary 2.6.
If  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  , then the inequality
, then the inequality 
Proof.
The proof follows since

is feasible from the second feasible inequality in Theorem 2.1(ii)  and
and  .
.
Corollary 2.7.
If  is
is  -contractive and
-contractive and  -Kannan with
-Kannan with  , then the inequality
, then the inequality 
Proof.
The proof follows directly since

are feasible from the third feasible inequality in Theorem 2.1(ii)  and
and  .
.
Remark 2.8.
It turns out from Definition 1.2 that if  has the
has the  property for some real constants
property for some real constants  and
and  , then it has also the
, then it has also the  ;
;  ,
,  . The subsequent result is concerned with some joint
. The subsequent result is concerned with some joint  ,
,  -Kannan and
-Kannan and  -contractiveness of a self-mapping
-contractiveness of a self-mapping  .
.
Theorem 2.9.
The following properties hold:
(i) is
is  -Kannan if it has the
-Kannan if it has the  -property for any real constants L and m which satisfy the constraints
-property for any real constants L and m which satisfy the constraints  ,
, 
 ,
,
(ii)assume that  is
is  -contractive. Then, it is also
-contractive. Then, it is also  -Kannan and it possesses the
-Kannan and it possesses the  -property for any real constant m which satisfies
-property for any real constant m which satisfies  ,
,
(iii)assume that  is
is  -Kannan and
-Kannan and  . Then
. Then  has the
has the  -property with
-property with  and
and  ,
,
(iv)assume that  is
is  -contractive with
-contractive with  and
and  . Then
. Then  is
is  -Kannan and it has the
-Kannan and it has the  -property with
-property with  and
and  .
.
Proof.
-
(i)
If
 has the
has the 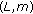 -property, one has from the triangle inequality for distances
-property, one has from the triangle inequality for distances  (2.11)
(2.11)
since  . The above inequality together with the triangle inequality leads to
. The above inequality together with the triangle inequality leads to

Thus,  is
is  -Kannan with
-Kannan with  which holds if
which holds if  and
and  . Property (i) is proven. Furthermore, if
. Property (i) is proven. Furthermore, if  is
is  -contractive then it is also
-contractive then it is also  -Kannan if
-Kannan if  with
with  from Theorem 2.1(ii). Then,
from Theorem 2.1(ii). Then,  is
is  -contractive,
-contractive,  -Kannan, and it has the
-Kannan, and it has the  -property if
-property if  which holds for
which holds for  if
if  and
and  which is already fulfilled since
which is already fulfilled since  is
is  -Kannan with the
-Kannan with the  -property. Property (ii) has been proven.
-property. Property (ii) has been proven.
-
(iii)
By using the triangle inequality for distances and taking
 and
and 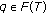 , one gets
, one gets  (2.13)
(2.13)
for any real constant  after using the subsequent relation:
after using the subsequent relation:

which follows directly from the  -Kannan property. Furthermore, since
-Kannan property. Furthermore, since  , the relation (2.14) leads to
, the relation (2.14) leads to


Then, the substitution of (2.16) into (2.13) yields

which proves Property (iii). Property (iv) is a direct consequence of Properties (ii)-(iii) since  is
is  -Kannan with
-Kannan with  .
.
Further results concerning  -Kannan mappings follow below.
-Kannan mappings follow below.
Theorem 2.10.
Assume that  is
is  -Kannan. Then, the following properties hold:
-Kannan. Then, the following properties hold:
(i) ;
;  ,
,  ,
,
(ii)if  is
is  -Kannan and
-Kannan and  -contractive, then
-contractive, then
(ii.1) ,
,
(ii.2) ,
,  ,
,  ,
,
(ii.3) ;
; ,
,  ,
,
(iii)if  is
is  -contractive for some
-contractive for some  , then
, then

 also,
also,  ;
;  ,
,  ,
,
(iv)if  is a complete metric space and
is a complete metric space and  is
is  -contractive for some
-contractive for some  or if it is
or if it is  -Kannan and
-Kannan and  -contractive, then
-contractive, then  is independent of
is independent of  ;
;  ,
,  so that
so that  consists of a unique fixed point.
consists of a unique fixed point.
Proof.
Proceed by complete induction by assuming that  ;
;  ,
,  . Since
. Since  is
is  -Kannan, take
-Kannan, take  so that one gets from the triangle inequality for distances and the above assumption for
so that one gets from the triangle inequality for distances and the above assumption for  that
that

Since  ;
;  , then
, then  so that
so that  ;
;  and the proof of Property (i) is complete.
and the proof of Property (i) is complete.
Property (ii.1) follows from Property (i), since  is
is  -Kannan, by taking into account that it is
-Kannan, by taking into account that it is  -contractive Property (ii.2) follows directly from Property (i) and Theorem 2.1(i). Property (ii.3) follows from
-contractive Property (ii.2) follows directly from Property (i) and Theorem 2.1(i). Property (ii.3) follows from

Property (iii) follows again directly from Property (i) and Theorem 2.1(i) and the first part of Property (ii) for  .
.
Property (iv) follows directly from Properties (ii) and (iii) from the uniqueness of the fixed point Banach's contraction mapping principle since  is a strict contraction.
is a strict contraction.
Proposition 2.11.
If is
is  -Kannan, then
-Kannan, then  ;
;  . If, in addition,
. If, in addition,  is
is  -contractive, then
-contractive, then  .
.
Proof.
It holds that

for all  by using the triangle property of distances and Theorem 2.10(i). The first part of the result has been proven. The second part of the result follows since
by using the triangle property of distances and Theorem 2.10(i). The first part of the result has been proven. The second part of the result follows since

if  is
is  -contractive.
-contractive.
Remark 2.12.
If is
is  -contractive and
-contractive and  -Kannan, it follows from Corollary 2.2 and Proposition 2.11 that
-Kannan, it follows from Corollary 2.2 and Proposition 2.11 that  ;
;  .
.
Proposition 2.13.
If is
is  -Kannan then
-Kannan then  ;
;  .
.
Proof.
It follows from Proposition 2.11 and Theorem 2.10(i) since

Proposition 2.14.
If is
is  -Kannan for some
-Kannan for some  , then
, then

Proof.
The upper-bound for  has been obtained in Proposition 2.11. Its lower-bound
has been obtained in Proposition 2.11. Its lower-bound  follows from Theorem 2.10(i) subject to
follows from Theorem 2.10(i) subject to  which holds
which holds  if and only if
if and only if  . The proof is complete.
. The proof is complete.
3. Combined Compatible Results about the  -Property,
-Property,  -Kannan-Mappings, and a Class of Expansive Mappings
-Kannan-Mappings, and a Class of Expansive Mappings
Definition 3.1 ([see [1]]).
Let  be a complete metric space. Also,
be a complete metric space. Also,  is said to be an
is said to be an  (
( )-times reasonable expansive self-mapping if there exists a real constant
)-times reasonable expansive self-mapping if there exists a real constant  such that
such that

Theorem 3.2.
Let  be a complete metric space. Assume that
be a complete metric space. Assume that  is a continuous surjective self-mapping which is continuous everywhere in
is a continuous surjective self-mapping which is continuous everywhere in  and
and  -Kannan while it also satisfies
-Kannan while it also satisfies  for some real constant
for some real constant  , some
, some  ,
,  (i.e.,
(i.e.,  is
is  (
( ) times reasonable expansive self-mapping). Then, the following properties hold if
) times reasonable expansive self-mapping). Then, the following properties hold if  :
:
(i) ;
;  ,
,
(ii) has a unique fixed point in
has a unique fixed point in  ,
,
(iii) has a fixed point in
has a fixed point in  even if it is not
even if it is not  -Kannan.
-Kannan.
Proof.
Since  is
is  -Kannan and it satisfies
-Kannan and it satisfies  ; some real constant
; some real constant  , some
, some  ,
,  , then
, then

Since  and
and  , then
, then

and Property (i) has been proven. Also,

The last expression can be rewritten as

where  is the identity mapping on X; that is,
is the identity mapping on X; that is,  ;
;  ,
,  is defined by
is defined by  ;
;  (and then it is a surjective mapping since
(and then it is a surjective mapping since  is surjective) and the functional
is surjective) and the functional  is defined as
is defined as  . It turns out that
. It turns out that  is continuous everywhere on its definition domain (and then lower semicontinuous bounded from below as a result) since the distance mapping
is continuous everywhere on its definition domain (and then lower semicontinuous bounded from below as a result) since the distance mapping  is continuous on
is continuous on  . Then,
. Then,  has a fixed point in
has a fixed point in  in [1, Lemma 2.4], even if
in [1, Lemma 2.4], even if  is not
is not  -Kannan, since f is surjective on
-Kannan, since f is surjective on  is the identity mapping on
is the identity mapping on  , and
, and  is lower semicontinuous bounded from below. The fixed point is unique since
is lower semicontinuous bounded from below. The fixed point is unique since  is a complete metric space. Properties (ii)-(iii) have been proven.
is a complete metric space. Properties (ii)-(iii) have been proven.
The subsequent result gives necessary conditions for Theorem 3.2 to hold as well as a sufficient condition for such a necessary condition to hold.
Theorem 3.3.
Let ( ) be a complete metric space. Assume that
) be a complete metric space. Assume that  is a surjective self-mapping which is continuous everywhere in X which satisfies
is a surjective self-mapping which is continuous everywhere in X which satisfies  for some real constant
for some real constant  , some
, some  ,
,  . The following holds. (i) The following zero limit exists
. The following holds. (i) The following zero limit exists

-
(ii)
If
 is
is  -Kannan then a sufficient condition for Property (i) to hold is:
-Kannan then a sufficient condition for Property (i) to hold is:  (3.7)
(3.7)
and a necessary condition for the above sufficient condition to hold is:

-
(iii)
If
 is
is  -Kannan then two joint necessary conditions for Property (i) to hold are:
-Kannan then two joint necessary conditions for Property (i) to hold are:  (3.9)
(3.9)
and such limits superior and inferior coincide as existing limits and are zero.
Proof.
-
(i)
Assume that Property (i) does not hold. Then,
 has not a fixed point in X what contradicts Theorem 3.2(iii). Thus, Property (i) holds.
has not a fixed point in X what contradicts Theorem 3.2(iii). Thus, Property (i) holds. -
(ii)
The condition
 ;
; 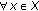 together with the
together with the  -Kannan property yield:
-Kannan property yield: 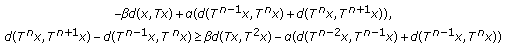 (3.10)
(3.10)
for all  . If
. If

then

with  ,
,  since
since

for all  so that
so that  as
as  is a a sufficient condition for Property (i) to hold. The necessary condition for the above sufficient to hold follows directly from the constraint
is a a sufficient condition for Property (i) to hold. The necessary condition for the above sufficient to hold follows directly from the constraint  ;
;  .
.
-
(iii)
It follows since the subsequent constraints follow directly from the hypotheses and
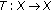 has a fixed point
has a fixed point  (3.14)
(3.14)
Theorem 3.2 may be generalized by generalizing the inequality  to eventually involve other powers of
to eventually involve other powers of  , not necessarily being respectively identical to (
, not necessarily being respectively identical to ( ) and
) and  , as follows.
, as follows.
Theorem 3.4.
Let  be a complete metric space. Then, the following properties hold.
be a complete metric space. Then, the following properties hold.
-
(i)
assume that
 is a surjective self-mapping which is continuous everywhere in X and satisfies:
is a surjective self-mapping which is continuous everywhere in X and satisfies:  (3.15)
(3.15)
for some real constants  ;
; some
some  ,
,  , then,
, then,  has at least a fixed point in X and it may eventually possess
has at least a fixed point in X and it may eventually possess  = card
= card fixed points in X.
fixed points in X.
-
(ii)
if Property (i) holds for
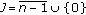 then
then  has at least a fixed point in X and, furthermore,
has at least a fixed point in X and, furthermore,  (3.16)
(3.16)
Proof.
-
(i)
From the statement constraints, it follows that
 (3.17)
(3.17)
so that

 ,
,  where each functional
where each functional  ;
;  is defined by
is defined by

and the functions  and
and  are defined, respectively, as
are defined, respectively, as  ,
,  ;
;  . Note that
. Note that  ,
,  is continuous, and then lower semicontinuous, on X;
is continuous, and then lower semicontinuous, on X;  since
since  and
and  are both continuous in X. Since
are both continuous in X. Since  is surjective then
is surjective then  is also surjective
is also surjective  so that
so that  and
and  are also surjective
are also surjective  . From [1, Lemma 2.4], they have a coincidence point since (3.18) holds and
. From [1, Lemma 2.4], they have a coincidence point since (3.18) holds and  ,
,  is continuous. Then, there exists
is continuous. Then, there exists  for some
for some  for each
for each  so that
so that  so that
so that  with
with  provided that
provided that  .
.
-
(ii)
It follows directly from Property (i), (3.18) and
 ;
; 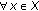 .
.
Remark 3.5.
Note that although  if
if  , it is not proven that
, it is not proven that  since some of the existing fixed points for
since some of the existing fixed points for  can mutually coincide or even more than one fixed point can eventually exist for each
can mutually coincide or even more than one fixed point can eventually exist for each  .
.
It is wellknown that nonexpansive and asymptotically non-expansive mappings can have fixed points as contractions have. See, for instance, [1, 2, 6, 14–18]. However, and generally speaking,  (
( )-times reasonable expansive self-mappings do not necessarily have a fixed point, although they might have them, [1]. It has been proven in [1] that continuous and surjective
)-times reasonable expansive self-mappings do not necessarily have a fixed point, although they might have them, [1]. It has been proven in [1] that continuous and surjective  (
( )-times reasonable expansive self-mappings
)-times reasonable expansive self-mappings  in complete metric spaces
in complete metric spaces  have a fixed pointing X if they fulfil the property:
have a fixed pointing X if they fulfil the property:

Proposition 3.6.
Assume that ;
;  ,
, , some real constant
, some real constant  . Then,
. Then,

for all 
 , some real constant
, some real constant  .
.
Proof.
It follows directly from (3.20) by interchanging  and
and  in (3.20).
in (3.20).
Proposition 3.7.
If (3.20) holds  ,
,  , then
, then

for all  ,
,  .
.
Proof.
Take  in (3.20).
in (3.20).
Proposition 3.8.
Assume that  is an (
is an ( )-times reasonable expansive self-mapping which satisfies (3.20) and
)-times reasonable expansive self-mapping which satisfies (3.20) and  is a complete metric space. Then
is a complete metric space. Then

Proof.
If follows from (3.20) and Proposition 3.6 that

for  provided that
provided that  , and
, and

for  provided that
provided that  .
.
Assume that (3.23) holds. Since  is an
is an  (
( )-times reasonable expansive self-mapping, there exists a real constant
)-times reasonable expansive self-mapping, there exists a real constant  such that
such that  ;
;  which is impossible since
which is impossible since  . Instead of (3.24) one can have:
. Instead of (3.24) one can have:

for  provided that
provided that  . Since
. Since  is an
is an  (
( ) times reasonable expansive self-mapping, there exists a real constant
) times reasonable expansive self-mapping, there exists a real constant  such that
such that

Then, either  so that
so that  , or
, or

and the proof is complete.
Proposition 3.8 may be rewritten in a more clear equivalent form as follows:
Proposition 3.9.
A necessary condition for a self-mapping  in complete metric space
in complete metric space  to be an
to be an  (
( ) times reasonable expansive self-mapping which satisfies Property (3.20) is that (3.23) holds.
) times reasonable expansive self-mapping which satisfies Property (3.20) is that (3.23) holds.
Theorem 2.10 of [1] may be reformulated subject to the above necessary condition as follows.
Theorem 3.10.
Assume that  is a complete metric space and that
is a complete metric space and that  is a continuous surjective
is a continuous surjective  (
( )-times reasonable expansive self-mapping which satisfies the constraint (3.20) and the necessary condition of Proposition 3.9. Then
)-times reasonable expansive self-mapping which satisfies the constraint (3.20) and the necessary condition of Proposition 3.9. Then  has a fixed point in X.
has a fixed point in X.
If the self-mapping  satisfies Theorem 3.10 and it is also
satisfies Theorem 3.10 and it is also  -Kannan, then the subsequent result holds:
-Kannan, then the subsequent result holds:
Theorem 3.11.
Assume that Theorem 3.10 holds. Then,  is in addition
is in addition  -Kannan if and only if
-Kannan if and only if

and the existing fixed point is unique.
-
(ii)
The following inequalities also hold:
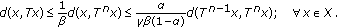 (3.30)
(3.30)
Proof.
The proof follows from (3.28) and the  -Kannan-property.
-Kannan-property.

which, together with (3.28), yields (3.29) since  . The fixed point of
. The fixed point of  (Theorem 3.10) is unique since
(Theorem 3.10) is unique since  is a complete metric space. Property (i) has been proven. Property (ii) is a direct result from Property (i) and (3.28).
is a complete metric space. Property (i) has been proven. Property (ii) is a direct result from Property (i) and (3.28).
Remark 3.12.
It is interesting to compare Theorem 3.2 with Theorem 3.11, subject to Proposition 3.9, and their respective guaranteed inequalities for distances in X for the case when  is simultaneously
is simultaneously  -Kannan and
-Kannan and  -times reasonable expansive self-mapping. Note that Theorem 3.2 is based on the fulfilment of the inequality
-times reasonable expansive self-mapping. Note that Theorem 3.2 is based on the fulfilment of the inequality  ;
;  , for some
, for some  for some real constant
for some real constant  while Theorem 3.11 is based on
while Theorem 3.11 is based on  ;
;  for some real constants
for some real constants  .
.
It is also of interest to investigate when  being a continuous surjective
being a continuous surjective  (
( )-times reasonable expansive self-mapping (Definition 3.1) satisfying either Theorem 3.10 or Theorem 3.2 has also the
)-times reasonable expansive self-mapping (Definition 3.1) satisfying either Theorem 3.10 or Theorem 3.2 has also the  -property for some real constants
-property for some real constants  and
and  (Definition 1.2). Note that if either Theorem 3.10 or Theorem 3.2 are fulfilled then
(Definition 1.2). Note that if either Theorem 3.10 or Theorem 3.2 are fulfilled then  so that Definition 1.2 is well-posed.
so that Definition 1.2 is well-posed.
Theorem 3.13.
The following properties hold:
-
(i)
assume that
 is a nonempty complete metric space and that
is a nonempty complete metric space and that 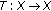 is a continuous surjective
is a continuous surjective  (
(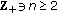 )-times reasonable expansive self-mapping according to Theorem 3.10 so that it has a fixed point in X . Then,
)-times reasonable expansive self-mapping according to Theorem 3.10 so that it has a fixed point in X . Then,  also possesses the
also possesses the 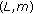 -property for some real constants
-property for some real constants  and
and  if
if 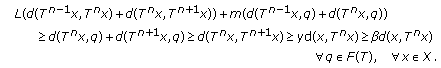 (3.32)
(3.32)
Two necessary conditions for the above condition to hold are:

provided that  ;
;  and
and

-
(ii)
assume that
 is a nonempty complete metric space and that
is a nonempty complete metric space and that  is a continuous surjective
is a continuous surjective  (
( ) times reasonable expansive self-mapping which satisfies Theorem 3.2. Then,
) times reasonable expansive self-mapping which satisfies Theorem 3.2. Then,  also possesses the
also possesses the  -property for some real constants
-property for some real constants 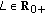 and
and  if and only if
if and only if  (3.35)
(3.35)
Two necessary conditions for the above necessary and sufficient condition to hold are,

provided that  ;
;  and
and  ;
;  , some real constant
, some real constant  .
.
Proof.
It follows from (3.28) and the  -property under direct calculations.
-property under direct calculations.
Remark 3.14.
Note from direct inspection of Definition 1.2 and the triangle property of distances that if  has the
has the  -property then for any
-property then for any  .
.

The subsequent results are focused on the combinations of one of the two conditions below, compatible under extra conditions with the existence of fixed points, with the  -property in a metric space
-property in a metric space  for some real constant
for some real constant  :
:
-
(a)
 (3.38)
(3.38)
where (see Theorem 3.2)
(see Theorem 3.2)
-
(b)
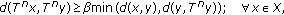 (3.39)
(3.39)
where  being a surjective
being a surjective  -times reasonable expansive self-mapping (see Propositions 3.7 and 3.8). Note by direct inspection that (3.40) is equivalent to
-times reasonable expansive self-mapping (see Propositions 3.7 and 3.8). Note by direct inspection that (3.40) is equivalent to

Theorem 3.15.
The following properties hold:(i) fulfils simultaneously (3.38) and the
fulfils simultaneously (3.38) and the  -property for some
-property for some  if
if

A necessary condition for (3.41) to hold is  ;
;  ,
,  .
.
Another necessary condition for (3.41) to hold is

provided that  and
and 
(ii) fulfils simultaneously (3.38) and the
fulfils simultaneously (3.38) and the  -property for some
-property for some  ,
,  if
if

Proof.
The sufficiency parts of Properties (i) and (ii) follow directly from Remark 3.14 and (3.38) and (3.39), respectively. The first necessary condition of Property (i) is a direct need for the lower-bound of  in (3.41) do not exceed its upper-bound,
in (3.41) do not exceed its upper-bound,  . The second necessary condition is proven as follows. From the first necessary condition and the triangle inequality for distances, one gets:
. The second necessary condition is proven as follows. From the first necessary condition and the triangle inequality for distances, one gets:

if 

 .
.
Theorem 3.16.
The following properties hold:
-
(i)
A necessary condition for (3.39) to hold with
 being an
being an 
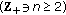 -times reasonable expansive self-mapping is
-times reasonable expansive self-mapping is

-
(ii)
A necessary condition for
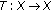 to possess, in addition, the
to possess, in addition, the 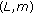 -property for some
-property for some  and
and  is
is

Proof.
-
(i)
Take
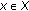 ,
,  so that
so that  (3.47)
(3.47)
There are two potential possibilities for each  , since (3.39) holds, namely, either:
, since (3.39) holds, namely, either:
-
(a)
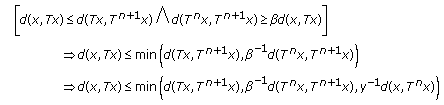 (3.48)
(3.48)
for some real constants  since, in addition,
since, in addition,  is
is  (
( )-times reasonable expansive, so that Property (i) holds directly, or
)-times reasonable expansive, so that Property (i) holds directly, or
-
(b)
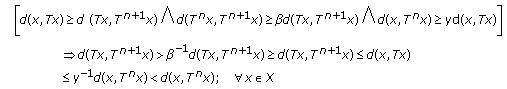 (3.49)
(3.49)
what leads to the contradiction  . Thus, the above result of logic implications cannot hold if
. Thus, the above result of logic implications cannot hold if  , as a result, if (3.39) holds then (3.48) is a necessary condition for
, as a result, if (3.39) holds then (3.48) is a necessary condition for  to be an
to be an  -times reasonable expansive self-mapping. Property (i) has been proven.
-times reasonable expansive self-mapping. Property (i) has been proven.
-
(ii)
Property (i) is equivalent to
 (3.50)
(3.50)
so that if  satisfies, in addition, the
satisfies, in addition, the  -property for some
-property for some  and
and  then:
then:
-
(a)
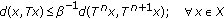 (3.51)
(3.51)
-
(b)
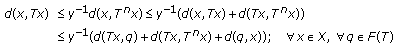 (3.52)
(3.52)

provided that 

 ,
,  provided that
provided that  . The combination of (3.52) to (3.54) proves the result.
. The combination of (3.52) to (3.54) proves the result.
4. Examples
Example 4.1.
Consider the one -dimensional linear unforced discrete dynamic system

under initial conditions  . The distance function is taken as the usual Euclidean norm, namely,
. The distance function is taken as the usual Euclidean norm, namely,  ;
;  . It turns out that if
. It turns out that if  then
then  as
as  irrespective of
irrespective of  so that
so that  is the only stable attractor, which is the only equilibrium point, and the system is globally asymptotically stable.
is the only stable attractor, which is the only equilibrium point, and the system is globally asymptotically stable.  is also the only fixed point of the self-mapping
is also the only fixed point of the self-mapping  on
on  in the complete metric space (
in the complete metric space ( ,
,  ) defined by
) defined by  ;
;  which is
which is  -contractive for any real
-contractive for any real  provided that
provided that  . It is now tested when
. It is now tested when  is
is  -Kannan. Note that
-Kannan. Note that

for any sequences  ;
;  ;
;  for initial conditions
for initial conditions  so that by combining the above three relations:
so that by combining the above three relations:

and  is
is  -Kannan if
-Kannan if  which is guaranteed for
which is guaranteed for  if
if  which is the condition of Theorem 2.1(i) guaranteeing that if
which is the condition of Theorem 2.1(i) guaranteeing that if  is
is  -contractive, it is also
-contractive, it is also  -Kannan.
-Kannan.
Example 4.2.
Now consider the  -th dimensional linear unforced discrete dynamic system
-th dimensional linear unforced discrete dynamic system

under initial conditions  where
where  is the
is the  (or spectral)-norm which coincides with the Euclidean (or Froebenius) norm for vectors. For the matrix
(or spectral)-norm which coincides with the Euclidean (or Froebenius) norm for vectors. For the matrix  , we define the vector-induced
, we define the vector-induced  -norm by
-norm by

where  is the maximum (real) eigenvalue of
is the maximum (real) eigenvalue of  . The distance function is taken as the usual Euclidean norm in
. The distance function is taken as the usual Euclidean norm in  , namely,
, namely,  ;
;  . Assume that
. Assume that  . Define the self-mapping
. Define the self-mapping  on
on  as
as  ;
;  . It follows that
. It follows that  is the only equilibrium point, which is stable, and
is the only equilibrium point, which is stable, and  . The relations obtained for the scalar case still hold with the replacements
. The relations obtained for the scalar case still hold with the replacements  ,
,  ,
,  ,
,  and the
and the  -contractive self-mapping
-contractive self-mapping  on
on  is also
is also  -Kannan if
-Kannan if  which is still the sufficient condition of Theorem 2.1.
which is still the sufficient condition of Theorem 2.1.
Example 4.3.
Now consider the  -th dimensional, perhaps nonlinear, unforced time-varying discrete dynamic system subject to perturbations:
-th dimensional, perhaps nonlinear, unforced time-varying discrete dynamic system subject to perturbations:

under initial conditions  and
and  is a uniformly bounded sequence of real
is a uniformly bounded sequence of real  -vectors
-vectors  for any bounded
for any bounded  whose elements satisfy
whose elements satisfy  . Now consider two solution sequences
. Now consider two solution sequences  ,
,  under initial conditions
under initial conditions  . Let
. Let  be defined from real finite constants
be defined from real finite constants  ,
,  where
where  provided that
provided that  , that is, all the matrices
, that is, all the matrices  ;
;  are stability matrices. Consider the distance being the Euclidean norm. If
are stability matrices. Consider the distance being the Euclidean norm. If  then,
then,

So that the solution sequence is bounded for any bounded initial conditions. Furthermore,

Thus, the self-mapping  is
is  -Kannan if
-Kannan if  , that is if
, that is if  , irrespective of its contractiveness or not. The above condition is guaranteed with
, irrespective of its contractiveness or not. The above condition is guaranteed with  and
and  .
.
Now, assume that the discrete dynamic system is defined by:

 for some
for some  . Then,
. Then,

since  provided that
provided that  . In this case, one also has:
. In this case, one also has:

Then the following hold.
(1)First,  is
is  -contractive with
-contractive with  with
with  being its unique stable equilibrium point and its unique fixed point provided that
being its unique stable equilibrium point and its unique fixed point provided that and
and  . The time-varying system is globally asymptotically stable.
. The time-varying system is globally asymptotically stable.
(2)If  , that is
, that is  and
and  then the
then the  -contractive self-mapping
-contractive self-mapping  is furthermore
is furthermore  -Kannan. Those results still agree with Theorem 2.1. On the other hand, the
-Kannan. Those results still agree with Theorem 2.1. On the other hand, the  -property of contractive Kannan self-mappings can be tested for this example according to the formula
-property of contractive Kannan self-mappings can be tested for this example according to the formula

from Theorem 2.9 with  with
with  ,
,  since
since  is
is  -Kannan and
-Kannan and  -contractive. Note that
-contractive. Note that

with the above lower-bound being reached for  ,
,  . Note also that
. Note also that  . since otherwise, one would have
. since otherwise, one would have

what is a contradiction.
Example 4.4.
A forced version of the equation of Example 4.1 is

with  . If
. If  then
then

independent of the initial condition for any bounded initial condition. Also, it is direct by complete induction the property

On the other hand, if  and
and  then
then

If, in addition, the system is positive and stable, that is  , with positive initial conditions
, with positive initial conditions  and forcing term
and forcing term  then
then  is not contractive since
is not contractive since  for any finite
for any finite  , and
, and

for any real  since it holds that
since it holds that

Thus, for 
 ,
,  , one has
, one has

so that the self-mapping  has a fixed point while it is reasonable expansive (see Definition 3.1 and Theorem 3.2). Extensions to the non positive first-order system and the
has a fixed point while it is reasonable expansive (see Definition 3.1 and Theorem 3.2). Extensions to the non positive first-order system and the  -th order discrete dynamic system can be addressed in the same way. If the system is time-varying with the sequence of parameters
-th order discrete dynamic system can be addressed in the same way. If the system is time-varying with the sequence of parameters  fulfilling
fulfilling  then
then  as
as  where
where  is the geometric mean of the elements of
is the geometric mean of the elements of  . Thus, there is still a unique fixed point
. Thus, there is still a unique fixed point  . Also, if there is a finite subset
. Also, if there is a finite subset  such that
such that  if and only if
if and only if  then there is a unique fixed point
then there is a unique fixed point  since
since  despite the fact that
despite the fact that  is not contractive.
is not contractive.
References
Chen CF, Zhu CX: Fixed point theorems for times reasonable expansive mapping. Fixed Point Theory and Applications 2008, 2008:-6.
Hu L-G: Strong convergence of a modified Halpern's iteration for nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-9.
Saeidi S: Approximating common fixed points of Lipschitzian semigroup in smooth Banach spaces. Fixed Point Theory and Applications 2008, 2008:-17.
De la Sen M: About robust stability of dynamic systems with time delays through fixed point theory. Fixed Point Theory and Applications 2008, 2008:-20.
Latif A, Abdou AAN: Fixed points of generalized contractive maps. Fixed Point Theory and Applications 2009, 2009:-9.
Xiao J-Z, Zhu X-H: Common fixed point theorems on weakly contractive and nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-8.
Karpagam S, Agrawal S: Best proximity point theorems for -cyclic Meir-Keeler contractions. Fixed Point Theory and Applications 2009, 2009:-9.
De la Sen M: Stability and convergence results based on fixed point theory for a generalized viscosity iterative scheme. Fixed Point Theory and Applications 2009, 2009:-19.
Qing Y, Rhoades BE: -stability of Picard iteration in metric spaces. Fixed Point Theory and Applications 2008, 2008:-4.
Kannan R: Some results on fixed points. II. The American Mathematical Monthly 1969,76(4):405–408. 10.2307/2316437
Kikkawa M, Suzuki T: Some similarity between contractions and Kannan mappings. Fixed Point Theory and Applications 2008, 2008:-8.
Enjouji Y, Nakanishi M, Suzuki T: A Generalization of Kannan's fixed point theorem. Fixed Point Theory and Applications 2009, 2009:-10.
Subrahmanyam PV: Completeness and fixed-points. Monatshefte für Mathematik 1975,80(4):325–330. 10.1007/BF01472580
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967,73(6):957–961. 10.1090/S0002-9904-1967-11864-0
Shioji N, Takahashi W: Strong convergence theorems for asymptotically nonexpansive semigroups in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 1998,34(1):87–99. 10.1016/S0362-546X(97)00682-2
Dominguez Benavides T, Acedo GL, Xu H-K: Construction of sunny nonexpansive retractions in Banach spaces. Bulletin of the Australian Mathematical Society 2002,66(1):9–16. 10.1017/S0004972700020621
Medghalchi A, Saeidi S: Weak and strong convergence for some of nonexpansive mappings. Taiwanese Journal of Mathematics 2008,12(9):2489–2499.
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1972,35(1):171–174. 10.1090/S0002-9939-1972-0298500-3
Acknowledgments
The author is grateful to the Spanish Ministry of Education by its partial support of this work through Grant DPI 2009-07197. He is also grateful to the Basque Government by its support through Grants GIC07143-IT-269-07and SAIOTEK S-PE08UN15. The author is also very grateful to the reviewers by their useful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M. Some Combined Relations between Contractive Mappings, Kannan Mappings, Reasonable Expansive Mappings, and  -Stability.
Fixed Point Theory Appl 2009, 815637 (2009). https://doi.org/10.1155/2009/815637
-Stability.
Fixed Point Theory Appl 2009, 815637 (2009). https://doi.org/10.1155/2009/815637
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/815637
 -Contractive Mappings,
-Contractive Mappings,  -Kannan Mappings, and the
-Kannan Mappings, and the  -Property
-Property is
is  -contractive, then
-contractive, then 
 is
is  -contractive and
-contractive and  -Kannan with
-Kannan with 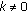 and
and  . For
. For  , the result holds trivially.
, the result holds trivially. with
with  where
where  is the (empty or nonempty) set of fixed points of
is the (empty or nonempty) set of fixed points of  . Since
. Since  , the inequality leads to
, the inequality leads to  . This implies that
. This implies that  since
since 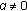 . However,
. However,  ;
; 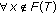 , what is a contradiction. Therefore, the inequality cannot cold in X.
, what is a contradiction. Therefore, the inequality cannot cold in X. :
: 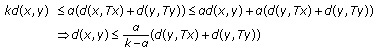
 has the
has the 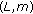 -property, one has from the triangle inequality for distances
-property, one has from the triangle inequality for distances 
 and
and 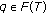 , one gets
, one gets 
 -Property,
-Property,  -Kannan-Mappings, and a Class of Expansive Mappings
-Kannan-Mappings, and a Class of Expansive Mappings is
is  -Kannan then a sufficient condition for Property (i) to hold is:
-Kannan then a sufficient condition for Property (i) to hold is: 
 is
is  -Kannan then two joint necessary conditions for Property (i) to hold are:
-Kannan then two joint necessary conditions for Property (i) to hold are: 
 has not a fixed point in X what contradicts Theorem 3.2(iii). Thus, Property (i) holds.
has not a fixed point in X what contradicts Theorem 3.2(iii). Thus, Property (i) holds. ;
; 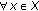 together with the
together with the  -Kannan property yield:
-Kannan property yield: 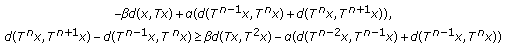
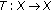 has a fixed point
has a fixed point 
 is a surjective self-mapping which is continuous everywhere in X and satisfies:
is a surjective self-mapping which is continuous everywhere in X and satisfies: 
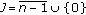 then
then  has at least a fixed point in X and, furthermore,
has at least a fixed point in X and, furthermore, 

 ;
; 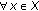 .
.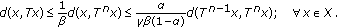
 is a nonempty complete metric space and that
is a nonempty complete metric space and that 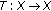 is a continuous surjective
is a continuous surjective  (
(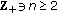 )-times reasonable expansive self-mapping according to Theorem 3.10 so that it has a fixed point in X . Then,
)-times reasonable expansive self-mapping according to Theorem 3.10 so that it has a fixed point in X . Then,  also possesses the
also possesses the 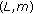 -property for some real constants
-property for some real constants  and
and  if
if 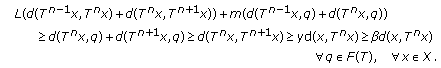
 is a nonempty complete metric space and that
is a nonempty complete metric space and that  is a continuous surjective
is a continuous surjective  (
( ) times reasonable expansive self-mapping which satisfies Theorem 3.2. Then,
) times reasonable expansive self-mapping which satisfies Theorem 3.2. Then,  also possesses the
also possesses the  -property for some real constants
-property for some real constants 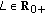 and
and  if and only if
if and only if 

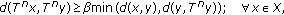
 being an
being an 
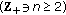 -times reasonable expansive self-mapping is
-times reasonable expansive self-mapping is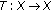 to possess, in addition, the
to possess, in addition, the 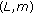 -property for some
-property for some  and
and  is
is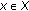 ,
,  so that
so that