- Research Article
- Open access
- Published:
On Strong Convergence by the Hybrid Method for Equilibrium and Fixed Point Problems for an Inifnite Family of Asymptotically Nonexpansive Mappings
Fixed Point Theory and Applications volume 2009, Article number: 798319 (2009)
Abstract
We introduce two modifications of the Mann iteration, by using the hybrid methods, for equilibrium and fixed point problems for an infinite family of asymptotically nonexpansive mappings in a Hilbert space. Then, we prove that such two sequences converge strongly to a common element of the set of solutions of an equilibrium problem and the set of common fixed points of an infinite family of asymptotically nonexpansive mappings. Our results improve and extend the results announced by many others.
1. Introduction
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  . A mapping
. A mapping  is said to be nonexpansive if for all
is said to be nonexpansive if for all  we have
we have  . It is said to be asymptotically nonexpansive [1] if there exists a sequence
. It is said to be asymptotically nonexpansive [1] if there exists a sequence  with
with  and
and  such that
such that  for all integers
for all integers  and for all
and for all  . The set of fixed points of
. The set of fixed points of  is denoted by
is denoted by  .
.
Let  be a bifunction, where
be a bifunction, where  is the set of real number. The equilibrium problem for the function
is the set of real number. The equilibrium problem for the function  is to find a point
is to find a point  such that
such that

The set of solutions of (1.1) is denoted by  . In 2005, Combettes and Hirstoaga [2] introduced an iterative scheme of finding the best approximation to the initial data when
. In 2005, Combettes and Hirstoaga [2] introduced an iterative scheme of finding the best approximation to the initial data when  is nonempty, and they also proved a strong convergence theorem.
is nonempty, and they also proved a strong convergence theorem.
For a bifunction  and a nonlinear mapping
and a nonlinear mapping  , we consider the following equilibrium problem:
, we consider the following equilibrium problem:

The set of such that  is denoted by
is denoted by  , that is,
, that is,

In the case of  ,
,  . In the case of
. In the case of  ,
,  is denoted by
is denoted by  . The problem (1.2) is very general in the sense that it includes, as special cases, some optimization problems, variational inequalities, minimax problems, the Nash equilibrium problem in noncooperative games, and others (see, e.g., [3, 4]).
. The problem (1.2) is very general in the sense that it includes, as special cases, some optimization problems, variational inequalities, minimax problems, the Nash equilibrium problem in noncooperative games, and others (see, e.g., [3, 4]).
Recall that a mapping  is called monotone if
is called monotone if

A mapping  of
of  into
into  is called
is called  -inverse strongly monotone, see [5–7], if there exists a positive real number
-inverse strongly monotone, see [5–7], if there exists a positive real number  such that
such that

for all  . It is obvious that any
. It is obvious that any  inverse strongly monotone mapping
inverse strongly monotone mapping  is monotone and Lipschitz continuous.
is monotone and Lipschitz continuous.
Construction of fixed points of nonexpansive mappings and asymptotically nonexpansive mappings is an important subject in nonlinear operator theory and its applications, in particular, in image recovery and signal processing (see, e.g., [1, 8–10]). Fixed point iteration processes for nonexpansive mappings and asymptotically nonexpansive mappings in Hilbert spaces and Banach spaces including Mann [11] and Ishikawa [12] iteration processes have been studied extensively by many authors to solve nonlinear operator equations as well as variational inequalities; see, for example, [11–13]. However, Mann and Ishikawa iteration processes have only weak convergence even in Hilbert spaces (see, e.g., [11, 12]).
Some attempts to modify the Mann iteration method so that strong convergence is guaranteed have recently been made. In 2003, Nakajo and Takahashi [14] proposed the following modification of the Mann iteration method for a nonexpansive mapping  in a Hilbert space
in a Hilbert space  :
:

where  denotes the metric projection from
denotes the metric projection from  onto a closed convex subset
onto a closed convex subset  of
of  . They proved that if the sequence
. They proved that if the sequence  bounded above from one, then
bounded above from one, then  defined by (1.6) converges strongly to
defined by (1.6) converges strongly to  .
.
Recently, Kim and Xu [15] adapted the iteration (1.6) to an asymptotically nonexpansive mapping in a Hilbert space  :
:

where  , as
, as  . They proved that if
. They proved that if  for all
for all  and for some
and for some  , then the sequence
, then the sequence  generated by (1.7) converges strongly to
generated by (1.7) converges strongly to  .
.
Very recently, Inchan and Plubtieng [16] introduced the modified Ishikawa iteration process by the shrinking hybrid method [17] for two asymptotically nonexpansive mappings  and
and  , with
, with  a closed convex bounded subset of a Hilbert space
a closed convex bounded subset of a Hilbert space  . For
. For  and
and  , define
, define  as follows:
as follows:

where  , as
, as  and
and  and
and  for all
for all  . They proved that the sequence
. They proved that the sequence  generated by (1.8) converges strongly to a common fixed point of two asymptotically nonexpansive mappings
generated by (1.8) converges strongly to a common fixed point of two asymptotically nonexpansive mappings  and
and  .
.
Zegeye and Shahzad [18] established the following hybrid iteration process for a finite family of asymptotically nonexpansive mappings in a Hilbert space  :
:

where  , as
, as  . Under suitable conditions strong convergence theorem is proved which extends and improves the corresponding results of Nakajo and Takahashi [14] and Kim and Xu [15].
. Under suitable conditions strong convergence theorem is proved which extends and improves the corresponding results of Nakajo and Takahashi [14] and Kim and Xu [15].
On the other hand, for finding a common element of  , Tada and Takahashi [19] introduced the following iterative scheme by the hybrid method in a Hilbert space:
, Tada and Takahashi [19] introduced the following iterative scheme by the hybrid method in a Hilbert space:  and let
and let

for every  , where
, where  for some
for some  and
and  satisfies
satisfies  . Further, they proved that
. Further, they proved that  and
and  converge strongly to
converge strongly to  , where
, where  .
.
Inspired and motivated by the above facts, it is the purpose of this paper to introduce the Mann iteration process for finding a common element of the set of common fixed points of an infinite family of asymptotically nonexpansive mappings and the set of solutions of an equilibrium problem. Then we prove some strong convergence theorems which extend and improve the corresponding results of Tada and Takahashi [19], Inchan and Plubtieng [16], Zegeye and Shahazad [18], and many others.
2. Preliminaries
We will use the following notations:
(1)" " for weak convergence and "
" for weak convergence and " " for strong convergence;
" for strong convergence;
(2) denotes the weak
denotes the weak  -limit set of
-limit set of  .
.
Let  be a real Hilbert space. It is well known that
be a real Hilbert space. It is well known that

for all  .
.
It is well known that  satisfies Opial's condition [20], that is, for any sequence
satisfies Opial's condition [20], that is, for any sequence  with
with  , the inequality
, the inequality

holds for every  with
with  . Hilbert space
. Hilbert space  satisfies the Kadec-Klee property [21, 22], that is, for any sequence
satisfies the Kadec-Klee property [21, 22], that is, for any sequence  with
with  and
and  together imply
together imply  .
.
We need some facts and tools in a real Hilbert space  which are listed as follows.
which are listed as follows.
Lemma 2.1 ([23]).
Let  be an asymptotically nonexpansive mapping defined on a nonempty bounded closed convex subset
be an asymptotically nonexpansive mapping defined on a nonempty bounded closed convex subset  of a Hilbert space
of a Hilbert space  . If
. If  is a sequence in
is a sequence in  such that
such that  and
and  , then
, then  .
.
Lemma 2.2 ([24]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and also give a real number
and also give a real number  . The set
. The set  is convex and closed.
is convex and closed.
Lemma 2.3 ([22]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be the (metric or nearest) projection from
be the (metric or nearest) projection from  onto
onto 
 i.e.,
i.e., is the only point in
is the only point in  such that
such that  . Given
. Given  and
and  . Then
. Then  if and only if it holds the relation:
if and only if it holds the relation:

For solving the equilibrium problem, let us assume that the bifunction  satisfies the following conditions (see [3]):
satisfies the following conditions (see [3]):
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  for any
for any  ;
;
(A3) is upper-hemicontinuous, that is, for each
is upper-hemicontinuous, that is, for each 

(A4) is convex and weakly lower semicontinuous for each
is convex and weakly lower semicontinuous for each  .
.
The following lemma appears implicity in [3].
Lemma 2.4 ([3]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a bifunction of
be a bifunction of  into
into  satisfying (A1)–(A4). Let
satisfying (A1)–(A4). Let  and
and  . Then, there exists
. Then, there exists  such that
such that

The following lemma was also given in [2].
Lemma 2.5 ([2]).
Assume that  satisfies (A1)–(A4). For
satisfies (A1)–(A4). For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

for all  . Then, the following holds
. Then, the following holds
(1) is single-valued;
is single-valued;
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,  .
.
This implies that  , that is,
, that is, is a nonexpansive mapping:
is a nonexpansive mapping:
(3) ;
;
(4) is a closed and convex set.
is a closed and convex set.
Definition 2.6 (see [25]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself, and let
into itself, and let  be a sequence of real numbers such that
be a sequence of real numbers such that  for every
for every  with
with  . For any
. For any  define a mapping
define a mapping  as follows:
as follows:

Such a mapping  is called the modified
is called the modified  -mapping generated by
-mapping generated by  and
and  .
.
Lemma 2.7 ([10, Lemma 4.1]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  and let
and let  be a sequence of real numbers with
be a sequence of real numbers with  for all
for all  and
and  for every
for every  and
and  for some
for some  . Let
. Let  be the modified
be the modified  -mapping generated by
-mapping generated by  and
and  . Let
. Let 


 for every
for every  and
and  . Then, the followings hold:
. Then, the followings hold:
-
(i)
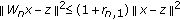 for all
for all 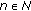 ,
,  and
and  ;
;
(ii) if  is bounded and
is bounded and  , for every sequence
, for every sequence  in C,
in C,

(iii) if  ,
,  and
and  is closed convex.
is closed convex.
Lemma 2.8 ([10, Lemma 4.4]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  . Let
. Let  for every
for every  , where
, where  for every
for every  and
and  with
with  for every
for every  and
and  for every
for every  and let
and let  for every
for every  . Then, the following holds:
. Then, the following holds:
(i) for all
for all  ,
,  and
and  ;
;
-
(ii)
if
 is bounded and
is bounded and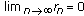 , for every sequence
, for every sequence  in C,
in C, 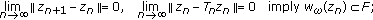 (2.9)
(2.9)
-
(iii)
if
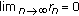 ,
, 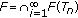 and
and 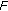 is closed convex.
is closed convex.
3. Main Results
In this section, we will introduce two iterative schemes by using hybrid approximation method for finding a common element of the set of common fixed points for a family of infinitely asymptotically nonexpansive mappings and the set of solutions of an equilibrium problem in Hilbert space. Then we show that the sequences converge strongly to a common element of the two sets.
Theorem 3.1.
Let  be a nonempty bounded closed convex subset of a real Hilbert space
be a nonempty bounded closed convex subset of a real Hilbert space  , let
, let  be a bifunction satisfying the conditions (A1)–(A4), let
be a bifunction satisfying the conditions (A1)–(A4), let  be an
be an  -inverse strongly monotone mapping of
-inverse strongly monotone mapping of  into
into  , let
, let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  , where
, where  and let
and let  be a sequence of real numbers with
be a sequence of real numbers with  for all
for all  and
and  for every
for every  and
and  for some
for some  . Let
. Let  be the modified
be the modified  -mapping generated by
-mapping generated by  and
and  . Assume that
. Assume that 

 for every
for every  and
and  such that
such that  . Let
. Let  and
and  be sequences generated by the following algorithm:
be sequences generated by the following algorithm:

where  and
and  and
and  and
and  . Then
. Then  and
and  converge strongly to
converge strongly to  .
.
Proof.
We show first that the sequences  and
and  are well defined.
are well defined.
We observe that  is closed and convex by Lemma 2.2. Next we show that
is closed and convex by Lemma 2.2. Next we show that  for all
for all  . we prove first that
. we prove first that  is nonexpansive. Let
is nonexpansive. Let  . Since
. Since  is
is  -inverse strongly monotone and
-inverse strongly monotone and  , we have
, we have

Thus  is nonexpansive.
is nonexpansive.
Since

we obtain

By Lemma 2.5, we have  ,
,  .
.
Let  , it follows the definition of
, it follows the definition of  that
that

So,

Again by Lemma 2.5, we have  ,
, .
.
Since  and
and  are nonexpansive, one has
are nonexpansive, one has

Then using the convexity of  and Lemma 2.7 we obtain that
and Lemma 2.7 we obtain that

So  for all
for all  and hence
and hence  for all
for all  . This implies that
. This implies that  is well defined. From Lemma 2.4, we know that
is well defined. From Lemma 2.4, we know that  is also well defined.
is also well defined.
Next, we prove that  ,
,  ,
,  ,
,  , as
, as  .
.
It follows from  that
that

So, for  , we have
, we have

This implies that

and hence

Since  is bounded, then
is bounded, then and
and  are bounded.
are bounded.
From  and
and  , we have
, we have

So,

This implies that

Hence,  is nodecreasing, and so
is nodecreasing, and so  exists.
exists.
Next, we can show that  . Indeed, From (2.1) and (3.13), we obtain
. Indeed, From (2.1) and (3.13), we obtain

Since  exists, we have
exists, we have

On the other hand, it follows from  that
that

It follows that

Next, we claim that  . Let
. Let  , it follows from (3.8) that
, it follows from (3.8) that

This implies that

It follows from (3.19) that

From Lemma 2.5, one has

This implies that

By (3.8), we have

Substituting (3.24) into (3.25), we obtain

which implies that

Noticing that  and (3.19), it follows from (3.27) that
and (3.19), it follows from (3.27) that

From (3.17) and (3.28), we have

Similarly, from (3.19) and (3.28), one has

Noticing that the condition  , it follows that
, it follows that

which implies that

Next, we prove that there exists a subsequence  of
of  which converges weakly to
which converges weakly to  , where
, where  .
.
Since  is bounded and
is bounded and  is closed, there exists a subsequence
is closed, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  , where
, where  . From (3.28), we have
. From (3.28), we have  . Noticing (3.29) and (3.32), it follows from Lemma 2.7 that
. Noticing (3.29) and (3.32), it follows from Lemma 2.7 that  . Next we prove that
. Next we prove that  . Since
. Since  , for any
, for any  we have
we have

From (A2), one has

Replacing  by
by  , we obtain
, we obtain

Put  for all
for all  and
and  . Then, we have
. Then, we have  . So we have
. So we have

Since  , we have
, we have  . Further, from monotonicity of
. Further, from monotonicity of  , we have
, we have  . So, from (A4) we have
. So, from (A4) we have

as  . From (A1) and (A4), we also have
. From (A1) and (A4), we also have

and hence

Letting  , we have, for each
, we have, for each  ,
,

This implies that  . Therefore
. Therefore  .
.
Finally we show that  ,
, , where
, where  .
.
Putting  and consider the sequence
and consider the sequence  . Then we have
. Then we have  and by the weak lower semicontinuity of the norm and by the fact that
and by the weak lower semicontinuity of the norm and by the fact that  for all
for all  which is implied by the fact that
which is implied by the fact that  , we obtain
, we obtain

This implies that  (hence
(hence  by the uniqueness of the nearest point projection of
by the uniqueness of the nearest point projection of  onto
onto  ) and that
) and that

It follows that  , and hence
, and hence  . Since
. Since  is an arbitrary (weakly convergent) subsequence of
is an arbitrary (weakly convergent) subsequence of  , we conclude that
, we conclude that  . From (3.28), we know that
. From (3.28), we know that  also. This completes the proof of Theorem 3.1.
also. This completes the proof of Theorem 3.1.
Theorem 3.2.
Let  be a nonempty bounded closed convex subset of a real Hilbert space
be a nonempty bounded closed convex subset of a real Hilbert space  , let
, let  be a bifunction satisfying the conditions (A1)–(A4), let
be a bifunction satisfying the conditions (A1)–(A4), let be an
be an  -inverse strongly monotone mapping of
-inverse strongly monotone mapping of  into
into  , and let
, and let be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  , where
, where  . Let
. Let  for every
for every  , where
, where  for every
for every  and
and  with
with  for each
for each  and
and  for every
for every  and assume that
and assume that  for every
for every  such that
such that  . Let
. Let  and
and  be sequences generated by
be sequences generated by

where  and
and  and
and  . Then
. Then  and
and  converge strongly to
converge strongly to  .
.
Proof.
We divide the proof of Theorem 3.2 into four steps.
(i)We show first that the sequences  and
and  are well defined.
are well defined.
From the definition of  and
and  , it is obvious that
, it is obvious that  is closed and
is closed and  is closed and convex for each
is closed and convex for each  . We prove that
. We prove that  is convex. Since
is convex. Since

is equivalent to

it follows that  is convex. So,
is convex. So,  is a closed convex subset of
is a closed convex subset of  for any
for any  .
.
Next, we show that  . Indeed, let
. Indeed, let  and let
and let  be a sequence of mappings defined as in Lemma 2.5. Similar to the proof of Theorem 3.1, we have
be a sequence of mappings defined as in Lemma 2.5. Similar to the proof of Theorem 3.1, we have

By virtue of the convexity of norm  , (3.46), and Lemma 2.8, we have
, (3.46), and Lemma 2.8, we have

Therefore,  for all
for all  .
.
Next, we prove that  ,
,  . For
. For  , we have
, we have  . Assume that
. Assume that  . Since
. Since  is the projection of
is the projection of  onto
onto  , by Lemma 2.3, we have
, by Lemma 2.3, we have

In particular, we have

for each  and hence
and hence  . Hence
. Hence  ,
,  . Therefore, we obtain that
. Therefore, we obtain that

This implies that  is well defined. From Lemma 2.4, we know that
is well defined. From Lemma 2.4, we know that  is also well defined.
is also well defined.
(ii)We prove that  ,
,  ,
,  ,
,  , as
, as  .
.
Since  is a nonempty closed convex subset of
is a nonempty closed convex subset of  , there exists a unique
, there exists a unique  such that
such that  .
.
From  , we have
, we have

Since  , we have
, we have

Since  is bounded, we have
is bounded, we have  ,
,  and
and  are bounded. From the definition of
are bounded. From the definition of  , we have
, we have  , which together with the fact that
, which together with the fact that  implies that
implies that

This shows that the sequence  is nondecreasing. So,
is nondecreasing. So, exists.
exists.
It follows from (2.1) and (3.53) that

Noticing that  exists, this implies that
exists, this implies that

Since  , we have
, we have

So, we have  . It follows that
. It follows that

Similar to the proof of Theorem 3.1, we have

From (3.55) and (3.58), we have

Similarly, from (3.57) and (3.58), one has

Noticing the condition  , it follows that
, it follows that

which implies that

-
(iii)
We prove that there exists a subsequence
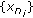 of
of 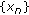 which converges weakly to
which converges weakly to  , where
, where 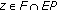 .
.
Since  is bounded and
is bounded and  is closed, there exists a subsequence
is closed, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  , where
, where  . From (3.58), we have
. From (3.58), we have  . Noticing (3.59) and (3.62), it follows from Lemma 2.8 that
. Noticing (3.59) and (3.62), it follows from Lemma 2.8 that  . By using the same method as in the proof of Theorem 3.1, we easily obtain that
. By using the same method as in the proof of Theorem 3.1, we easily obtain that  .
.
-
(iv)
Finally we show that
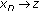 ,
, 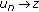 , where
, where  .
.
Since  and
and  , we have
, we have

It follows from  and the weak lower-semicontinuity of the norm that
and the weak lower-semicontinuity of the norm that

Thus, we obtain that  . Using the Kadec-Klee property of
. Using the Kadec-Klee property of  , we obtain that
, we obtain that

Since  is an arbitrary subsequence of
is an arbitrary subsequence of  , we conclude that
, we conclude that  converges strongly to
converges strongly to  . By (3.58), we have
. By (3.58), we have  also. This completes the proof of Theorem 3.2.
also. This completes the proof of Theorem 3.2.
Corollary 3.3.
Let  be a nonempty bounded closed convex subset of a real Hilbert space
be a nonempty bounded closed convex subset of a real Hilbert space  , let
, let  be a bifunction satisfying the conditions (A1)–(A4), let
be a bifunction satisfying the conditions (A1)–(A4), let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  , where
, where  and let
and let  be a sequence of real numbers with
be a sequence of real numbers with  for all
for all  and
and  for every
for every  and
and  for some
for some  . Let
. Let  be the modified
be the modified  -mapping generated by
-mapping generated by  and
and  . Assume that
. Assume that 


 for every
for every  and
and  such that
such that  . Let
. Let  and
and  be sequences generated by the following algorithm:
be sequences generated by the following algorithm:

where  and
and  and
and  and
and  such that
such that  . Then
. Then  and
and  converge strongly to
converge strongly to  .
.
Proof.
Putting  , the conclusion of Corollary 3.3 can be obtained as in the proof of Theorem 3.1.
, the conclusion of Corollary 3.3 can be obtained as in the proof of Theorem 3.1.
Remark 3.4.
Corollary 3.3 extends the Theorem of Tada and Takahashi [19] in the following senses:
(1)from one nonexpansive mapping to a family of infinitely asymptotically nonexpansive mappings;
-
(2)
from computation point of view, the algorithm in Corollary 3.3 is also simpler and, more convenient to compute than the one given in [19].
Corollary 3.5.
Let  be a nonempty bounded closed convex subset of a real Hilbert space
be a nonempty bounded closed convex subset of a real Hilbert space  , let
, let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  and let
and let  be a sequence of real numbers with
be a sequence of real numbers with  for all
for all  and
and  for every
for every  and
and  for some
for some  . Let
. Let  be the modified
be the modified  -mapping generated by
-mapping generated by  and
and  . Assume that
. Assume that 


 for every
for every  and
and  such that
such that  . Let
. Let  be a sequence generated by the following algorithm:
be a sequence generated by the following algorithm:

where  and
and  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
Putting  ,
,  ,
,  and
and  , for all
, for all  in Theorem 3.1, we have
in Theorem 3.1, we have  , therefore
, therefore  . The conclusion of Corollary 3.5 can be obtained from Theorem 3.1 immediately.
. The conclusion of Corollary 3.5 can be obtained from Theorem 3.1 immediately.
Remark 3.6.
Corollary 3.5 extends Theorem 3.1 of Inchan and Plubtieng [16] from two asymptotically nonexpansive mappings to an infinite family of asymptotically nonexpansive mappings.
Corollary 3.7.
Let  be a nonempty bounded closed convex subset of a real Hilbert space
be a nonempty bounded closed convex subset of a real Hilbert space  , and let
, and let  be a family of asymptotically nonexpansive mappings of
be a family of asymptotically nonexpansive mappings of  into itself with Lipschitz constants
into itself with Lipschitz constants  , that is,
, that is,  (
( ) such that
) such that  . Let
. Let  for every
for every  , where
, where  for every
for every  and
and  with
with  for each
for each  and
and  for every
for every  and assume that
and assume that  for every
for every  such that
such that  . Let
. Let  be a sequence generated by
be a sequence generated by

where  and
and  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
Putting  ,
,  ,
,  and
and  , for all
, for all  in Theorem 3.2, we have
in Theorem 3.2, we have  , therefore
, therefore  . The conclusion of Corollary 3.7 can be obtained from Theorem 3.2.
. The conclusion of Corollary 3.7 can be obtained from Theorem 3.2.
Remark 3.8.
Corollary 3.7 extends Theorem 3.1 of Zegeye and Shahzad [18] from a finite family of asymptotically nonexpansive mappings to an infinite family of asymptotically nonexpansive mappings.
References
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Moudafi A, Théra M: Proximal and dynamical approaches to equilibrium problems. In Ill-Posed Variational Problems and Regularization Techniques, Lecture Notes in Economics and Mathematical Systems. Volume 477. Springer, Berlin, Germany; 1999:187–201.
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Liu F, Nashed MZ: Regularization of nonlinear ill-posed variational inequalities and convergence rates. Set-Valued Analysis 1998,6(4):313–344. 10.1023/A:1008643727926
Nakajo K, Takahashi W: Strong and weak convergence theorems by an improved splitting method. Communications on Applied Nonlinear Analysis 2002,9(2):99–107.
Podilchuk CI, Mammone RJ: Image recovery by convex projections using a least-squares constraint. Journal of the Optical Society of America A 1990, 7: 517–521.
Byrne C: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Problems 2004,20(1):103–120. 10.1088/0266-5611/20/1/006
Nakajo K, Shimoji K, Takahashi W: On strong convergence by the hybrid method for families of mappings in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(1–2):112–119. 10.1016/j.na.2008.10.034
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974, 44: 147–150. 10.1090/S0002-9939-1974-0336469-5
Tan K-K, Xu HK: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. Journal of Mathematical Analysis and Applications 1993,178(2):301–308. 10.1006/jmaa.1993.1309
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. Journal of Mathematical Analysis and Applications 2003,279(2):372–379. 10.1016/S0022-247X(02)00458-4
Kim T-H, Xu H-K: Strong convergence of modified Mann iterations for asymptotically nonexpansive mappings and semigroups. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):1140–1152. 10.1016/j.na.2005.05.059
Inchan I, Plubtieng S: Strong convergence theorems of hybrid methods for two asymptotically nonexpansive mappings in Hilbert spaces. Nonlinear Analysis: Hybrid Systems 2008,2(4):1125–1135. 10.1016/j.nahs.2008.09.006
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2008,341(1):276–286. 10.1016/j.jmaa.2007.09.062
Zegeye H, Shahzad N: Strong convergence theorems for a finite family of asymptotically nonexpansive mappings and semigroups. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4496–4503. 10.1016/j.na.2007.11.005
Tada A, Takahashi W: Weak and strong convergence theorems for a nonexpansive mapping and an equilibrium problem. Journal of Optimization Theory and Applications 2007,133(3):359–370. 10.1007/s10957-007-9187-z
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Lin P-K, Tan K-K, Xu HK: Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 1995,24(6):929–946. 10.1016/0362-546X(94)00128-5
Martinez-Yanes C, Xu H-K: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2400–2411. 10.1016/j.na.2005.08.018
Takahashi W: Weak and strong convergence theorems for families of nonexpansive mappings and their applications. Annales Universitatis Mariae Curie-Sklodowska. Sectio A 1997,51(2):277–292.
Acknowledgments
This research is supported by the National Science Foundation of China under Grant (10771175), and by the key project of chinese ministry of education(209078) and the Natural Science Foundational Committee of Hubei Province (D200722002).
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cai, G., Hu, C. On Strong Convergence by the Hybrid Method for Equilibrium and Fixed Point Problems for an Inifnite Family of Asymptotically Nonexpansive Mappings. Fixed Point Theory Appl 2009, 798319 (2009). https://doi.org/10.1155/2009/798319
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/798319
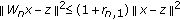 for all
for all 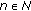 ,
,  and
and  ;
; is bounded and
is bounded and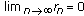 , for every sequence
, for every sequence  in C,
in C, 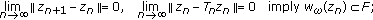
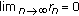 ,
, 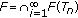 and
and 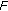 is closed convex.
is closed convex.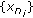 of
of 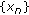 which converges weakly to
which converges weakly to  , where
, where 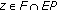 .
.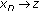 ,
, 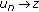 , where
, where  .
.