- Research Article
- Open access
- Published:
On  -Stability of Picard Iteration in Cone Metric Spaces
-Stability of Picard Iteration in Cone Metric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 751090 (2009)
Abstract
The aim of this work is to investigate the  -stability of Picard's iteration procedures in cone metric spaces and give an application.
-stability of Picard's iteration procedures in cone metric spaces and give an application.
1. Introduction and Preliminary
Let  be a real Banach space. A nonempty convex closed subset
be a real Banach space. A nonempty convex closed subset  is called a cone in
is called a cone in  if it satisfies the following:
if it satisfies the following:
(i) is closed, nonempty, and
is closed, nonempty, and  ,
,
(ii) , and
, and  imply that
imply that 
(iii) and
and  imply that
imply that 
The space  can be partially ordered by the cone
can be partially ordered by the cone  ; by defining,
; by defining,  if and only if
if and only if  . Also, we write
. Also, we write  if
if  int
int  , where int
, where int  denotes the interior of
denotes the interior of  .
.
A cone  is called normal if there exists a constant
is called normal if there exists a constant  such that
such that  implies
implies  .
.
In the following we always suppose that  is a real Banach space,
is a real Banach space,  is a cone in
is a cone in  , and
, and  is the partial ordering with respect to
is the partial ordering with respect to  .
.
Definition 1.1 (see [1]).
Let  be a nonempty set. Assume that the mapping
be a nonempty set. Assume that the mapping  satisfies the following:
satisfies the following:
(i) for all
for all  and
and  if and only if
if and only if  ,
,
(ii) for all
for all  ,
,
(iii) for all
for all  .
.
Then  is called a cone metric on
is called a cone metric on  , and
, and  is called a cone metric space.
is called a cone metric space.
Definition 1.2.
Let  be a map for which there exist real numbers
be a map for which there exist real numbers  satisfying
satisfying  . Then
. Then  is called a Zamfirescu operator if, for each pair
is called a Zamfirescu operator if, for each pair  ,
,  satisfies at least one of the following conditions:
satisfies at least one of the following conditions:
(1) ,
,
(2) ,
,
(3) .
.
Every Zamfirescu operator  satisfies the inequality:
satisfies the inequality:

for all  , where
, where  max
max , with
, with  . For normed spaces see [2].
. For normed spaces see [2].
Lemma 1.3 (see [3]).
Let  and
and  be nonnegative real sequences satisfying the following inequality:
be nonnegative real sequences satisfying the following inequality:

where  for all
for all 
 and
and  as
as  Then
Then 
Remark 1.4.
Let  and
and  be nonnegative real sequences satisfying the following inequality:
be nonnegative real sequences satisfying the following inequality:

where  for all
for all  and for some positive integer number
and for some positive integer number  . If
. If  as
as  Then
Then 
Lemma 1.5.
Let  be a normal cone with constant
be a normal cone with constant  , and let
, and let  and
and  be sequences in
be sequences in  satisfying the following inequality:
satisfying the following inequality:

where  and
and  as
as  Then
Then 
Proof.
Let  be a positive integer such that
be a positive integer such that  By recursion we have
By recursion we have

so

and then by Remark 1.4?? Therefore
Therefore 
2. 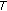 -Stability in Cone Metric Spaces
-Stability in Cone Metric Spaces
Let  be a cone metric space, and
be a cone metric space, and  a self-map of
a self-map of  . Let
. Let  be a point of
be a point of  , and assume that
, and assume that  is an iteration procedure, involving
is an iteration procedure, involving  , which yields a sequence
, which yields a sequence  of points from
of points from  .
.
Definition 2.1 (see [4]).
The iteration procedure  is said to be
is said to be  -stable with respect to
-stable with respect to  if
if  converges to a fixed point
converges to a fixed point  of
of  and whenever
and whenever  is a sequence in
is a sequence in  with
with  we have
we have 
In practice, such a sequence  could arise in the following way. Let
could arise in the following way. Let  be a point in
be a point in  . Set
. Set  . Let
. Let  . Now
. Now  . Because of rounding or discretization in the function
. Because of rounding or discretization in the function  , a new value
, a new value  approximately equal to
approximately equal to  might be obtained instead of the true value of
might be obtained instead of the true value of  . Then to approximate
. Then to approximate  , the value
, the value  is computed to yield
is computed to yield  , an approximation of
, an approximation of  . This computation is continued to obtain
. This computation is continued to obtain  an approximate sequence of
an approximate sequence of  .
.
One of the most popular iteration procedures for approximating a fixed point of  is Picard's iteration defined by
is Picard's iteration defined by  . If the conditions of Definition 2.1 hold for
. If the conditions of Definition 2.1 hold for  then we will say that Picard's iteration is
then we will say that Picard's iteration is  -stable.
-stable.
Recently Qing and Rhoades [5] established a result for the  -stability of Picard's iteration in metric spaces. Here we are going to generalize their result to cone metric spaces and present an application.
-stability of Picard's iteration in metric spaces. Here we are going to generalize their result to cone metric spaces and present an application.
Theorem 2.2.
Let  be cone metric space,
be cone metric space,  a normal cone, and
a normal cone, and  with
with  If there exist numbers
If there exist numbers  and
and  such that
such that

for each  and in addition, whenever
and in addition, whenever  is a sequence with
is a sequence with  as
as  , then Picard's iteration is
, then Picard's iteration is  -stable.
-stable.
Proof.
Suppose  and
and  We shall show that
We shall show that  Since
Since

if we put  and
and  in Lemma 1.5, then we have
in Lemma 1.5, then we have 
Note that the fixed point  of
of  is unique. Because if
is unique. Because if  is another fixed point of
is another fixed point of  , then
, then

which implies 
Corollary 2.3.
Let  be a cone metric space,
be a cone metric space,  a normal cone, and
a normal cone, and  with
with  If there exists a number
If there exists a number  such that
such that  for each
for each  then Picard's iteration is
then Picard's iteration is  -stable.
-stable.
Corollary 2.4.
Let  be a cone metric space,
be a cone metric space,  a normal cone, and
a normal cone, and  is a Zamfirescu operator with
is a Zamfirescu operator with  and whenever
and whenever  is a sequence with
is a sequence with  as
as  , then Picard's iteration is
, then Picard's iteration is  -stable.
-stable.
Definition 2.5 (see [6]).
Let  be a cone metric space. A map
be a cone metric space. A map  is called a quasicontraction if for some constant
is called a quasicontraction if for some constant  and for every
and for every  there exists
there exists  such that
such that 
Lemma 2.6.
If  is a quasicontraction with
is a quasicontraction with  , then
, then  is a Zamfirescu operator and so satisfies (2.1).
is a Zamfirescu operator and so satisfies (2.1).
Proof.
Let  for every
for every  we have
we have  for some
for some  In the case that
In the case that  we have
we have

So

Put  so
so  The other cases are similarly proved. Therefore
The other cases are similarly proved. Therefore  is a Zamfirescu operator.
is a Zamfirescu operator.
Theorem 2.7.
Let  be a nonempty complete cone metric space,
be a nonempty complete cone metric space,  be a normal cone, and
be a normal cone, and  a quasicontraction and self map of
a quasicontraction and self map of  with some
with some  Then Picard's iteration is
Then Picard's iteration is  -stable.
-stable.
Proof.
By [6, Theorem??2.1],  has a unique fixed point
has a unique fixed point  Also
Also  satisfies (2.1). So by Theorem 2.2 it is enough to show that
satisfies (2.1). So by Theorem 2.2 it is enough to show that  We have
We have

Put  and
and  Therefore
Therefore  as
as  and
and

where

Hence we have  or
or  where
where  or
or  and
and  or
or  Therefore by (2.7),
Therefore by (2.7),  by
by  Now by Lemma 1.5 we have
Now by Lemma 1.5 we have 
3. An Application
Theorem 3.1.
Let  with
with  for
for  and let
and let  be a self map of
be a self map of  defined by
defined by  where
where
(a) is a continuous function,
is a continuous function,
(b)the partial derivative  of
of  with respect to
with respect to  exists and
exists and  for some
for some 
(c)for every real number  one has
one has  for every
for every 
Let  be a normal cone and
be a normal cone and  the complete cone metric space defined by
the complete cone metric space defined by  where
where  Then,
Then,
(i)Picard's iteration is  -stable if
-stable if  ,
,
(ii)Picard's iteration fails to be  -stable if
-stable if  and
and 
Proof.
-
(i)
We have
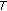 being a continuous quasicontraction map with
being a continuous quasicontraction map with  so by Theorem 2.7, Picard's iteration is
so by Theorem 2.7, Picard's iteration is 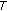 -stable.
-stable. -
(ii)
Put
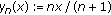 so
so 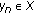 and
and  where
where 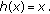 Also
Also 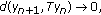 since
since  (3.1)
(3.1)
as  But
But  and
and  is not a fixed point for
is not a fixed point for  Therefore Picard's iteration is not
Therefore Picard's iteration is not  -stable.
-stable.
Example 3.2.
Let  and
and  Therefore
Therefore  and
and  satisfy the hypothesis of Theorem 3.1 where
satisfy the hypothesis of Theorem 3.1 where  has property (i) and
has property (i) and  has property (ii). So the self maps
has property (ii). So the self maps  of
of  defined by
defined by  and
and  have unique fixed points but Picard's iteration is
have unique fixed points but Picard's iteration is  -stable for
-stable for  but not
but not  -stable for
-stable for 
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Zhiqun X: Remarks of equivalence among Picard, Mann, and Ishikawa iterations in normed spaces. Fixed Point Theory and Applications 2007, 2007:-5.
Vasilev FP: Numerical Methodes for Solving Extremal Problems. 2nd edition. Nauka, Moscow, Russian; 1988:550.
Harder AM, Hicks TL: Stability results for fixed point iteration procedures. Mathematica Japonica 1988,33(5):693–706.
Qing Y, Rhoades BE: -stability of Picard iteration in metric spaces. Fixed Point Theory and Applications 2008, 2008:-4.
Ilic D, Rakocevic V: Quasi-contraction on a cone metric space. Applied Mathematics Letters 2009,22(5):728–731. 10.1016/j.aml.2008.08.011
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Asadi, M., Soleimani, H., Vaezpour, S.M. et al. On  -Stability of Picard Iteration in Cone Metric Spaces.
Fixed Point Theory Appl 2009, 751090 (2009). https://doi.org/10.1155/2009/751090
-Stability of Picard Iteration in Cone Metric Spaces.
Fixed Point Theory Appl 2009, 751090 (2009). https://doi.org/10.1155/2009/751090
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/751090
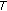 -Stability in Cone Metric Spaces
-Stability in Cone Metric Spaces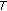 being a continuous quasicontraction map with
being a continuous quasicontraction map with  so by Theorem 2.7, Picard's iteration is
so by Theorem 2.7, Picard's iteration is 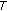 -stable.
-stable.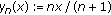 so
so 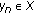 and
and  where
where 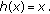 Also
Also 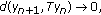 since
since 