- Research Article
- Open access
- Published:
Common Fixed Point Theorems for Weakly Compatible Pairs on Cone Metric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 643840 (2009)
Abstract
We prove several fixed point theorems on cone metric spaces in which the cone does not need to be normal. These theorems generalize the recent results of Huang and Zhang (2007), Abbas and Jungck (2008), and Vetro (2007). Furthermore as corollaries, we obtain recent results of Rezapour and Hamlborani (2008).
1. Introduction and Preliminaries
Recently, Abbas and Jungck [1], have studied common fixed point results for noncommuting mappings without continuity in cone metric space with normal cone. In this paper, our results are related to the results of Abbas and Jungck, but our assumptions are more general, and also we generalize some results of [1–3], and [4] by omitting the assumption of normality in the results.
Let us mention that nonconvex analysis, especially ordered normed spaces, normal cones, and topical functions ([2, 4–9]) have some applications in optimization theory. In these cases, an order is introduced by using vector space cones. Huang and Zhang [2] used this approach, and they have replaced the real numbers by ordering Banach space and defining cone metric space. Consistent with Huang and Zhang [2], the following definitions and results will be needed in the sequel.
Let  be a real Banach space. A subset
be a real Banach space. A subset  of
of  is called a cone if and only if:
is called a cone if and only if:
(i) is closed, nonempty, and
is closed, nonempty, and 
(ii) and
and  imply
imply 
(iii)
Given a cone  we define a partial ordering
we define a partial ordering  on
on  with respect to
with respect to  by
by  if and only if
if and only if  We will write
We will write  to indicate that
to indicate that  but
but  while
while  will stand for
will stand for  (interior of
(interior of  ). A cone
). A cone  is called normal if there are a number
is called normal if there are a number  such that for all
such that for all 

The least positive number satisfying the above inequality is called the normal constant of  It is clear that
It is clear that  From [4] we know that there exists ordered Banach space
From [4] we know that there exists ordered Banach space  with cone
with cone  which is not normal but with
which is not normal but with 
Definition 1.1 (see [2]).
Let  be a nonempty set. Suppose that the mapping
be a nonempty set. Suppose that the mapping  satisfies
satisfies
(d1) for all
for all  and
and  if and only if
if and only if 
(d2) for all
for all 
(d3) for all
for all 
Then  is called a cone metric on
is called a cone metric on  , and
, and  is called a cone metric space. The concept of a cone metric space is more general than of a metric space.
is called a cone metric space. The concept of a cone metric space is more general than of a metric space.
Definition 1.2 (see [2]).
Let  be a cone metric space. We say that
be a cone metric space. We say that  is
is
(e)Cauchy sequence if for every  in
in  with
with  there is an
there is an  such that for all
such that for all 
(f)convergent sequence if for every  in
in  with
with  there is an
there is an  such that for all
such that for all  for some fixed
for some fixed  in
in 
A cone metric space  is said to be complete if every Cauchy sequence in
is said to be complete if every Cauchy sequence in  is convergent in
is convergent in  The sequence
The sequence  converges to
converges to  if and only if
if and only if  as
as  It is a Cauchy if and only if
It is a Cauchy if and only if  as
as  .
.
Remark 1.3.
[10] Let  be an ordered Banach (normed) space. Then
be an ordered Banach (normed) space. Then  is an interior point of
is an interior point of  if and only if
if and only if  is a neighborhood of
is a neighborhood of 
Corollary 1.4 (see, e.g., [11] without proof).
-
(1)
If
 and
and  then
then 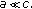
Indeed,  implies
implies 
-
(2)
If
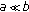 and
and 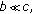 then
then 
Indeed,  implies
implies 
-
(3)
If
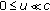 for each
for each 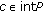 , then
, then 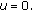
Remark 1.5.
If  ,
,  and
and  then there exists
then there exists  such that for all
such that for all  we have
we have  .
.
Proof.
Let  be given. Choose a symmetric neighborhood
be given. Choose a symmetric neighborhood  such that
such that  Since
Since  , there is
, there is  such that
such that  for
for  This means that
This means that  for
for  that is,
that is, 
From this it follows that: the sequence  converges to
converges to  if
if  as
as  and
and  is a Cauchy if
is a Cauchy if  as
as  In the situation with non-normal cone, we have only half of the lemmas 1 and 4 from [2]. Also, the fact that
In the situation with non-normal cone, we have only half of the lemmas 1 and 4 from [2]. Also, the fact that  if
if  and
and  is not applicable.
is not applicable.
Remark 1.6.
Let  If
If  and
and  then eventually
then eventually  where
where  are sequence and given point in
are sequence and given point in 
Proof.
It follows from Remark 1.5, Corollary 1.4(1), and Definition 1.2(f).
Remark 1.7.
If  and
and  then
then  for each cone
for each cone 
Remark 1.8.
If  is a real Banach space with cone
is a real Banach space with cone  and if
and if  where
where  and
and  then
then 
Proof.
The condition  means that
means that  that is,
that is,  Since
Since  and
and  then also
then also  Thus we have
Thus we have  and
and 
Remark 1.9.
Let  be a cone metric space. Let us remark that the family
be a cone metric space. Let us remark that the family  , where
, where  , is a subbasis for topology on
, is a subbasis for topology on  . We denote this cone topology by
. We denote this cone topology by  , and note that
, and note that  is a Hausdorff topology (see, e.g., [11] without proof).
is a Hausdorff topology (see, e.g., [11] without proof).
For the proof of the last statement, we suppose that for each  ,
,  we have
we have  . Thus, there exists
. Thus, there exists  such that
such that  and
and  . Hence,
. Hence,  . Clearly, for each
. Clearly, for each  , we have
, we have  , so
, so  . Now,
. Now,  , that is,
, that is,  , and we have
, and we have  .
.
We find it convenient to introduce the following definition.
Definition 1.10.
Let  be a cone metric space and
be a cone metric space and  a cone with nonempty interior. Suppose that the mappings
a cone with nonempty interior. Suppose that the mappings  are such that the range of
are such that the range of  contains the range of
contains the range of  , and
, and  or
or  is a complete subspace of
is a complete subspace of  . In this case we will say that the pair
. In this case we will say that the pair  is Abbas and Jungck's pair, or shortly AJ's pair.
is Abbas and Jungck's pair, or shortly AJ's pair.
Definition 1.11 (see [1]).
Let  and
and  be self-maps of a set
be self-maps of a set  (i.e.,
(i.e.,  )
)  If
If  for some
for some  in
in  then
then  is called a coincidence point of
is called a coincidence point of  and
and  and
and  is called a point of coincidence of
is called a point of coincidence of  and
and  Self-maps
Self-maps  and
and  are said to be weakly compatible if they commute at their coincidence point, that is, if
are said to be weakly compatible if they commute at their coincidence point, that is, if  for some
for some  then
then 
Proposition 1.12 (see [1]).
Let  and
and  be weakly compatible self-maps of a set
be weakly compatible self-maps of a set  If
If  and
and  have a unique point of coincidence
have a unique point of coincidence  then
then  is the unique common fixed point of
is the unique common fixed point of  and
and 
2. Main Results
In this section we will prove some fixed point theorems of contractive mappings for cone metric space. We generalize some results of [1–4] by omitting the assumption of normality in the results.
Theorem 2.1.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every  there exists
there exists

such that

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Let  and let
and let  be such that
be such that  . Having defined
. Having defined  let
let  be such that
be such that 
We first show that

We have that

where

Now we have to consider the following three cases.
If  then clearly (2.3) holds. If
then clearly (2.3) holds. If  then according to Remark 1.8
then according to Remark 1.8 and (2.3) is immediate. Finally, suppose that
and (2.3) is immediate. Finally, suppose that  Now,
Now,

Hence,  , and we proved (2.3).
, and we proved (2.3).
Now, we have

We will show that  is a Cauchy sequence. For
is a Cauchy sequence. For  , we have
, we have

and we obtain

From Remark 1.5 it follows that for  and large
and large  thus, according to Corollary 1.4(1),
thus, according to Corollary 1.4(1),  Hence, by Definition 1.2(e),
Hence, by Definition 1.2(e),  is a Cauchy sequence. Since
is a Cauchy sequence. Since  and
and  or
or  is complete, there exists a
is complete, there exists a  such that
such that  as
as  Consequently, we can find
Consequently, we can find  such that
such that 
Let us show that  For this we have
For this we have

where

Let  Clearly at least one of the following four cases holds for infinitely many
Clearly at least one of the following four cases holds for infinitely many  .
.
(case 10)

(case 20)

(case 30)

(case 40)

In all cases, we obtain  for each
for each  Using Corollary 1.4(3), it follows that
Using Corollary 1.4(3), it follows that  or
or 
Hence, we proved that  and
and  have a coincidence point
have a coincidence point  and a point of coincidence
and a point of coincidence  such that
such that  If
If  is another point of coincidence, then there is
is another point of coincidence, then there is  with
with  Now,
Now,

where

Hence,  that is,
that is, 
Since  is the unique point of coincidence of
is the unique point of coincidence of  and
and  and
and  and
and  are weakly compatible,
are weakly compatible,  is the unique common fixed point of
is the unique common fixed point of  and
and  by Proposition 1.12 [1].
by Proposition 1.12 [1].
In the next theorem, among other things, we generalize the well-known Zamfirescu result [12, ( )].
)].
Theorem 2.2.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every  there exists
there exists

such that

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover, if
. Moreover, if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Let  and let
and let  be such that
be such that  . Having defined
. Having defined  let
let  be such that
be such that 
We first show that

Notice that

where

As in Theorem 2.1, we have to consider three cases.
If  , then clearly (2.20) holds. If
, then clearly (2.20) holds. If  then from (2.19) with
then from (2.19) with  and
and  as
as  we have
we have

Hence,  and in this case (2.20) holds. Finally, if
and in this case (2.20) holds. Finally, if  then
then

and (2.20) holds. Thus, we proved that in all three cases (2.20) holds.
Now, from the proof of Theorem 2.1, we know that  is a Cauchy sequence. Hence, there exist
is a Cauchy sequence. Hence, there exist  in
in  and
and  such that
such that  ,
,  and
and 
Now we have to show that  For this we have
For this we have

where

Let  Clearly at least one of the following three cases holds for infinitely many
Clearly at least one of the following three cases holds for infinitely many  .
.
(case 10)

(case 20)

(case 30)

In all cases we obtain  for each
for each  Using Corollary 1.4(3), it follows that
Using Corollary 1.4(3), it follows that  or
or 
Thus we showed that  and
and  have a coincidence point
have a coincidence point  that is, point of coincidence
that is, point of coincidence  such that
such that  If
If  is another point of coincidence then there is
is another point of coincidence then there is  with
with  Now from (2.19), it follows that
Now from (2.19), it follows that

where

Hence,  that is,
that is,  If
If  and
and  are weakly compatible, then as in the proof of Theorem 2.1, we have that
are weakly compatible, then as in the proof of Theorem 2.1, we have that  is a unique common fixed point of
is a unique common fixed point of  and
and  The assertion of the theorem follows.
The assertion of the theorem follows.
Now as corollaries, we recover and generalize the recent results of Huang and Zhang [2], Abbas and Jungck [1], and Vetro [3]. Furthermore as corollaries, we obtain recent results of Rezapour and Hamlborani [4].
Corollary 2.3.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every 

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
Corollary 2.4.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every 

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
Corollary 2.5.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every 

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
In the next corollary, among other things, we generalize the well-known result [12, ( )].
)].
Corollary 2.6.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every  there exists
there exists

such that

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
Now, we generalize the well-known Bianchini result [12, (5)].
Corollary 2.7.
Suppose that  is AJ's pair, and that for some constant
is AJ's pair, and that for some constant  and for every
and for every  there exists
there exists

such that

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
When in the next theorem we set  the identity map on
the identity map on  and
and  , we get the theorem of Hardy and Rogers [12, (18)].
, we get the theorem of Hardy and Rogers [12, (18)].
Theorem 2.8.
Suppose that  is AJ's pair, and that there exist nonnegative constants
is AJ's pair, and that there exist nonnegative constants  satisfying
satisfying  such that, for each
such that, for each 

Then  and
and  have a unique coincidence point in
have a unique coincidence point in  . Moreover if
. Moreover if  and
and  are weakly compatible,
are weakly compatible,  and
and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Let us define the sequences  and
and  as in the proof of Theorem 2.1 We have to show that
as in the proof of Theorem 2.1 We have to show that

From

we obtain

Thus,

where  and we proved (2.40).
and we proved (2.40).
Now, from the proof of Theorem 2.1, we know that  is a Cauchy sequence. Hence, there exist
is a Cauchy sequence. Hence, there exist  in
in  and
and  such that
such that  ,
,  and
and 
We have to show that  For this we have
For this we have

Then according to Corollary 1.4(3),  , that is,
, that is, 
Thus we showed that  and
and  have a coincidence point
have a coincidence point  that is, point of coincidence
that is, point of coincidence  such that
such that  If
If  is another point of coincidence then there is
is another point of coincidence then there is  with
with  Now,
Now,

According to Remark 1.8, and because  we get
we get  that is,
that is,  If
If  and
and  are weakly compatible, then as in the proof of Theorem 2.1, we have that
are weakly compatible, then as in the proof of Theorem 2.1, we have that  is a unique common fixed point of
is a unique common fixed point of  and
and  The assertion of the theorem follows.
The assertion of the theorem follows.
It is clear that, for the special choice of  in Theorem 2.8, all the results from Corollaries 2.3, 2.4, and 2.5, could be obtained.
in Theorem 2.8, all the results from Corollaries 2.3, 2.4, and 2.5, could be obtained.
Finally, we add an example with Banach type contraction on non-normal cone metric space (see Corollary 2.3).
Example 2.9.
Let  , and
, and  Define
Define  by
by  where
where  such that
such that  It is easy to see that
It is easy to see that  is a cone metric on
is a cone metric on  Consider the mappings
Consider the mappings  in the following manner:
in the following manner:

where  One can see that
One can see that

for all  where
where  The mappings
The mappings  and
and  commute at
commute at  the only coincidence point. So
the only coincidence point. So  and
and  are weakly compatible. All the conditions of the Corollary 2.3 hold, then
are weakly compatible. All the conditions of the Corollary 2.3 hold, then  and
and  have a common fixed point.
have a common fixed point.
References
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. Journal of Mathematical Analysis and Applications 2008,341(1):416–420. 10.1016/j.jmaa.2007.09.070
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Vetro P: Common fixed points in cone metric spaces. Rendiconti del Circolo Matematico di Palermo 2007,56(3):464–468. 10.1007/BF03032097
Rezapour Sh, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Aliprantis CD, Tourky R: Cones and Duality, Graduate Studies in Mathematics. Volume 84. American Mathematical Society, Providence, RI, USA; 2007:xiv+279.
Mohebi H: Topical functions and their properties in a class of ordered Banach spaces. In Continuous Optimization, Applied Optimization. Volume 99. Springer, New York, NY, USA; 2005:343–361. 10.1007/0-387-26771-9_12
Raja P, Vaezpour SM: Some extensions of Banach's contraction principle in complete cone metric spaces. Fixed Point Theory and Applications 2008, -11.
Ilic D, Rakocevic V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Ilic D, Rakocevic V: Quasi-contraction on a cone metric spacestar, open. Applied Mathematics Letters 2009,22(5):728–731. 10.1016/j.aml.2008.08.011
Wong Y-C, Ng K-F: Partially Ordered Topological Vector Spaces, Oxford Mathematical Monograph. Clarendon Press, Oxford, UK; 1973:x+217.
Rezapour Sh: A review on topological properties of cone metric spaces. Analysis, Topology and Applications (ATA '08), May-June 2008, Vrnjacka Banja, Serbia
Rhoades BE: A comparison of various definitions of contractive mappings. Transactions of the American Mathematical Society 1977, 226: 257–290.
Acknowledgments
The fourth author would like to express his gratitude to Professor Sh. Rezapour and to Professor S. M. Veazpour for the valuable comments. The second, third, and fourth authors thank the Ministry of Science and the Ministry of Environmental Protection of Serbia for their support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jungck, G., Radenovic, S., Radojevic, S. et al. Common Fixed Point Theorems for Weakly Compatible Pairs on Cone Metric Spaces. Fixed Point Theory Appl 2009, 643840 (2009). https://doi.org/10.1155/2009/643840
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/643840
 and
and  then
then 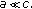
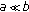 and
and 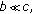 then
then 
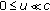 for each
for each 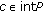 , then
, then