- Research Article
- Open access
- Published:
On Generalized Implicit Vector Equilibrium Problems in Topological Ordered Spaces
Fixed Point Theory and Applications volume 2009, Article number: 513408 (2009)
Abstract
We discuss three classes of generalized implicit vector equilibrium problems in topological ordered spaces. Under some conditions, we prove three new existence theorems of solutions for the generalized implicit vector equilibrium problems in topological ordered spaces by using the Fan-Browder fixed point theorem.
1. Introduction and Preliminaries
It is well known that the vector equilibrium problem is closely related to vector variational inequality, vector optimization problem, and many others (see, e.g., [1–6] and the references therein).
Recently, a large of generalized vector equilibrium problems have been studied in different conditions by many authors and a lot of results concerned with the existence of solutions and properties of solutions have been given in finite and infinite dimensional spaces (see [7] and the references therein).
The main purpose of this paper is to extend some known results for vector equilibrium problems to topological ordered spaces (see [8]). We discuss three classes of generalized implicit vector equilibrium problems in topological ordered spaces. Under some conditions, we prove three new existence theorems of solutions for the generalized implicit vector equilibrium problems in topological ordered spaces by using the Fan-Browder fixed point theorem.
A semilattice is a partially ordered set  , with the partial ordering denoted by
, with the partial ordering denoted by  , for which any pair
, for which any pair  of elements has a least upper bound, denoted by
of elements has a least upper bound, denoted by  . It is easy to see that any nonempty finite subset
. It is easy to see that any nonempty finite subset  of
of  has a least upper bound, denoted by sup
has a least upper bound, denoted by sup  . In the case
. In the case  , the set
, the set  is called an order interval. Now assume that
is called an order interval. Now assume that  is a semilattice and
is a semilattice and  is a nonempty finite subset. Thus, the set
is a nonempty finite subset. Thus, the set

is well defined and it has the following properties:
(a) ,
,
(b)if  , then
, then  .
.
A subset  is said to be
is said to be  -convex if, for any nonempty finite subset
-convex if, for any nonempty finite subset  , we have
, we have  .
.
For any  denotes the family of all finite subsets of
denotes the family of all finite subsets of  and
and

Let  be a topological semilattice,
be a topological semilattice,  a nonempty
a nonempty  -convex subset,
-convex subset,  a Hausdorff topological vector space. Assume that
a Hausdorff topological vector space. Assume that  ,
,  ,
,  , and
, and  such that, for any
such that, for any  ,
,  is a closed, pointed, and convex cone in
is a closed, pointed, and convex cone in  and
and  .
.
In this paper, we consider the following three classes generalized implicit vector equilibrium problems:
 weak generalized implicit vector equilibrium problem (WGIVEP): find
weak generalized implicit vector equilibrium problem (WGIVEP): find  , such that
, such that  and for any
and for any  , there exists an
, there exists an  such that
such that

 strong generalized implicit vector equilibrium problem (SGIVEP): find
strong generalized implicit vector equilibrium problem (SGIVEP): find  such that
such that  and
and

 uniform generalized implicit vector equilibrium problem (UGIVEP): find
uniform generalized implicit vector equilibrium problem (UGIVEP): find  such that
such that  and there exists
and there exists  such that
such that

Definition 1.1.
Let  and
and  be two topological spaces.
be two topological spaces.
 A mapping
A mapping  is called upper semicontinuous (usc) at
is called upper semicontinuous (usc) at  if, for any neighborhood
if, for any neighborhood  of
of  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that

F is called usc on  if it is usc at each point of
if it is usc at each point of  .
.
 A mapping
A mapping  is called lower semicontinuous (lsc) at
is called lower semicontinuous (lsc) at  if, for any net
if, for any net  in
in  such that
such that  and for any
and for any  , there exists
, there exists  such that
such that  .
.  is called lsc on
is called lsc on  if it is lsc at each point of
if it is lsc at each point of  .
.
 A mapping
A mapping  is called complement pseudo-upper semicontinuous (c p-usc) at
is called complement pseudo-upper semicontinuous (c p-usc) at  if, for
if, for  with
with  , we have
, we have  .
.  is called c p-usc on
is called c p-usc on  if
if  is c p-usc at each point
is c p-usc at each point  of
of  .
.
Remark 1.2.
 By [9], if
By [9], if  is usc with closed values, then for any net
is usc with closed values, then for any net  in
in  such that
such that  and for any net
and for any net  in
in  with
with  such that
such that  in
in  , we have
, we have  .
.
 If
If  is usc with closed values, then
is usc with closed values, then  is c p-usc, where
is c p-usc, where

Lemma 1.3 (see [9]).
Let  and
and  be two topological spaces. Let
be two topological spaces. Let  be compact and
be compact and  be usc such that
be usc such that  is compact for each
is compact for each  . Then
. Then  is compact.
is compact.
Definition 1.4.
Let  be a topological semilattice or a
be a topological semilattice or a  -convex subset of a topological semilattice, let
-convex subset of a topological semilattice, let  be a Hausdorff topological vector space, and let
be a Hausdorff topological vector space, and let  be a closed, pointed, and convex cone with
be a closed, pointed, and convex cone with  .
.
 A mapping
A mapping  is called a
is called a  -convex mapping (or a
-convex mapping (or a  -concave mapping) with respect to
-concave mapping) with respect to  if, for any nonempty finite subset
if, for any nonempty finite subset  ,
,  ,
,  ,
,  with
with  and
and  , there exists
, there exists  such that
such that

 A mapping
A mapping  is called to have
is called to have  -inheritance if, for any nonempty finite subset
-inheritance if, for any nonempty finite subset  of
of  ,
,  ,
,  with
with  and
and  , we have
, we have  .
.
 Let
Let  . A mapping
. A mapping  is called
is called  -
- -convex (or
-convex (or  -
- -concave) with respect to
-concave) with respect to  in second argument if, for any nonempty finite subset
in second argument if, for any nonempty finite subset  ,
,  ,
,  ,
,  ,
,  with
with  and
and  , there exists
, there exists  such that
such that

Remark 1.5.
If  is a
is a  -
- -convex mapping (or a
-convex mapping (or a  -
- -concave mapping) with respect to
-concave mapping) with respect to  in second argument, then for any
in second argument, then for any  ,
,  is a
is a  -convex mapping (or a
-convex mapping (or a  -concave mapping) with respect to
-concave mapping) with respect to  .
.
Lemma 1.6 (see [10]).
Let  be a nonempty compact
be a nonempty compact  -convex subset of a topological semilattice with path-connected intervals
-convex subset of a topological semilattice with path-connected intervals  , let
, let  be a mapping with nonempty
be a mapping with nonempty  -convex values such that, for each
-convex values such that, for each  ,
,  is an open set in
is an open set in  . Then
. Then  has a fixed point.
has a fixed point.
2. Existence Theorems
Theorem 2.1.
Let  be a nonempty compact
be a nonempty compact  -convex subset of a topological semilattice with path-connected intervals
-convex subset of a topological semilattice with path-connected intervals  , let
, let  be a Hausdorff topological vector space. Let
be a Hausdorff topological vector space. Let  be a mapping with nonempty
be a mapping with nonempty  -convex values, and let
-convex values, and let  and
and  be mappings and
be mappings and  be a mapping such that, for each
be a mapping such that, for each  ,
,  is a closed, pointed, and convex cone in
is a closed, pointed, and convex cone in  with
with  . Assume that
. Assume that
(1)For any  ,
,  is open;
is open;
(2) is closed;
is closed;
(3) is usc with compact values;
is usc with compact values;
(4) for any
for any  and
and  ;
;
(5)for any  and
and  ,
,  is
is  -concave with respect to
-concave with respect to  ;
;
(6)for any  ,
,  is lsc;
is lsc;
(7) is usc, where
is usc, where  for each
for each  .
.
Then there exists an  such that
such that  and for any
and for any  , there exists an
, there exists an  such that
such that

Furthermore, the solution set of (WGIVEP) is closed, and hence is compact.
Proof.
Define  by
by

We first prove that for any  ,
,  is open, that is,
is open, that is,

is closed. Let a net  and
and  . Then there exists
. Then there exists  such that
such that  ,
,  , for any
, for any  . By
. By  and Lemma 1.3, we know that
and Lemma 1.3, we know that

is compact and so  has a cluster point
has a cluster point  . We may assume that
. We may assume that  and thus,
and thus,  . For any
. For any  , by
, by  , there exists
, there exists  such that
such that  and so
and so  . It follows from
. It follows from  that
that  and hence
and hence  . Thus,
. Thus,  is closed and so
is closed and so  is open.
is open.
Suppose that there exists an  such that
such that  is not
is not  -convex, that is, there exist
-convex, that is, there exist  such that
such that  . Hence, there exists
. Hence, there exists  ,
,  , that is, there exists
, that is, there exists  such that
such that  . For each
. For each  ,
,  , take
, take  ,
,  . Let
. Let  ,
,  . For any
. For any  ,
,  and
and  , we have
, we have  . By
. By  , there exists
, there exists  such that
such that

Since  , we know that
, we know that

which is a contradiction. Therefore, for any  ,
,  is
is  -convex.
-convex.
By  and Lemma 1.6,
and Lemma 1.6,  . Define
. Define  by
by

Then  is
is  -convex for each
-convex for each  . It follows from
. It follows from  and
and  that
that

is open.
Suppose that for all  ,
,  is nonempty. Then, by Lemma 1.6
is nonempty. Then, by Lemma 1.6  has a fixed point, that is, there exists
has a fixed point, that is, there exists  , such that
, such that  . If
. If  , then
, then  , hence
, hence  , for all
, for all  ,
,  which contradicts to assumption
which contradicts to assumption  ; If
; If  , then
, then  , hence
, hence  which contradicts with
which contradicts with  . Therefore, there exists
. Therefore, there exists  , such that
, such that  . Since
. Since  is nonempty for any
is nonempty for any  , then
, then  ,
,  , that is,
, that is,  and for any
and for any  ,
,  . Therefore,
. Therefore,  and for any
and for any  , there exists an
, there exists an  such that
such that

Let  denote the solution set of (WGIVEP) and
denote the solution set of (WGIVEP) and  with
with  . We show that
. We show that  , that is,
, that is,  , and for all
, and for all  , there exists
, there exists  such that
such that

In fact, it follows from  that
that  . For any
. For any  ,
,  . By
. By  , there exists an open neighborhood
, there exists an open neighborhood  of
of  such that
such that  . Since
. Since  , there exists
, there exists  such that for any
such that for any  ,
,  . Thus,
. Thus,  and so there exists
and so there exists  such that
such that  , that is,
, that is,  . Since
. Since  is compact,
is compact,  has a cluster point
has a cluster point  . We may assume that
. We may assume that  . From
. From  , we have
, we have  . By
. By  , for any
, for any  , there exists
, there exists  such that
such that  . It follows from
. It follows from  that
that  , that is,
, that is,  . Thus,
. Thus,  is closed, and hence is compact. This completes the proof.
is closed, and hence is compact. This completes the proof.
Theorem 2.2.
Let  be a nonempty compact
be a nonempty compact  -convex subset of a topological semilattice with path-connected intervals
-convex subset of a topological semilattice with path-connected intervals  , let
, let  be a Hausdorff topological vector space. Let
be a Hausdorff topological vector space. Let  be with nonempty
be with nonempty  -convex values, and let
-convex values, and let  and
and  be mappings and
be mappings and  be a mapping such that, for each
be a mapping such that, for each  ,
,  is a closed, pointed, and convex cone in
is a closed, pointed, and convex cone in  with
with  . Assume that
. Assume that
(1)For any  ,
,  is open;
is open;
(2) is closed;
is closed;
(3) is lsc;
is lsc;
(4)for all  and
and  ,
,  ;
;
(5)for all  ,
,  is
is  -concave with respect to
-concave with respect to  in second argument;
in second argument;
(6)for all  ,
,  is lsc;
is lsc;
(7) is usc, where
is usc, where  for all
for all  .
.
Then there exists an  such that
such that  and
and

Furthermore, the solution set of (SGIVEP) is closed, and hence is compact.
Proof.
Define  by
by

Then the proof is similar to that of Theorem 2.1 and so we omit it.
Theorem 2.3.
Let  be a nonempty compact
be a nonempty compact  -convex subset of a topological semilattice with path-connected intervals
-convex subset of a topological semilattice with path-connected intervals  and let
and let  be a Hausdorff topological vector space. Let
be a Hausdorff topological vector space. Let  be with nonempty
be with nonempty  -convex values, let
-convex values, let  and
and  be mappings, and let
be mappings, and let  be a mapping such that, for each
be a mapping such that, for each  ,
,  is a closed, pointed, and convex cone in
is a closed, pointed, and convex cone in  with
with  . Assume that
. Assume that
(1) is usc with compact values;
is usc with compact values;
(2)For any  ,
,  is nonempty
is nonempty  -convex;
-convex;
(3) is c p-usc on
is c p-usc on  ;
;
(4) is usc with nonempty compact values;
is usc with nonempty compact values;
(5)for all  ,
,  ;
;
-
(6)
for all
 ,
,  is
is  -concave with respect to
-concave with respect to  ;
;
(7) has
has  -inheritance;
-inheritance;
(8) is c p-usc on
is c p-usc on  .
.
Then there exists an  such that
such that  and there exists
and there exists  such that
such that

Proof.
Define  by
by

where

The proof is divided into the following five steps.
-
(I)
For any
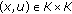 ,
, 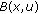 is nonempty.
is nonempty.
If it is false, then there exists  such that
such that  , that is, for any
, that is, for any  , there exists
, there exists  such that
such that  . Let
. Let

Then  is nonempty values. If there exists
is nonempty values. If there exists  such that
such that  is not
is not  -convex, then there exist
-convex, then there exist  such that
such that  , that is, there exists
, that is, there exists  with
with  . Thus,
. Thus,  . For each
. For each  ,
,  , take
, take  . For any
. For any  ,
,  and
and  , we have
, we have  . By
. By  , there exists
, there exists  such that
such that

Since  ,
,  . Hence,
. Hence,

which is a contradiction. Thus, for any  ,
,  is nonempty
is nonempty  -convex.
-convex.
For any  ,
,

It follows from  that
that

is closed and so  is open. Since
is open. Since  is nonempty compact and
is nonempty compact and  -convex, by Lemma 1.6
-convex, by Lemma 1.6  has a fixed point. Thus, there exists
has a fixed point. Thus, there exists  such that
such that  , that is,
, that is,  which contradicts with Assumption
which contradicts with Assumption  . Hence
. Hence  for any
for any  .
.
-
(II)
For any
 ,
,  is
is 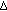 -convex. If it is false, then there exists
-convex. If it is false, then there exists 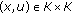 such that
such that  is not
is not  -convex, that is, there exist
-convex, that is, there exist  such that
such that

Thus, there exists  such that
such that  . Then
. Then  and for all
and for all  ,
,  ,
,  . Since
. Since  is
is  -convex,
-convex,  . By
. By  ,
,  . Since
. Since  , there exists
, there exists  such that
such that

which is a contradiction. Therefore, for any  ,
,  is
is  -convex.
-convex.
-
(III)
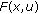 is nonempty
is nonempty 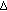 -convex for any
-convex for any 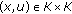 . By steps (I) and (II), the conclusion follows directly from
. By steps (I) and (II), the conclusion follows directly from 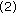 .
. -
(IV)
For any
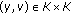 ,
,

is open. In fact, we only need to show that

is closed. Let a net  and
and  . If
. If  , then
, then  and hence
and hence

If  and there exists
and there exists  such that
such that

Take  . By
. By  and Lemma 1.3,
and Lemma 1.3,  is compact and hence
is compact and hence  has a cluster point
has a cluster point  . We may assume that
. We may assume that  and so
and so  . Similarly, by
. Similarly, by  ,
,  has a cluster point
has a cluster point  . We assume that
. We assume that  and hence
and hence  . Since
. Since  closed,
closed,  . Thus,
. Thus,  ,
,  and
and  . Hence,
. Hence,  is closed. Let a net
is closed. Let a net

and  , then
, then  . By
. By  , we have
, we have  , and hence
, and hence  is closed. Thus,
is closed. Thus,  is closed and so
is closed and so  is open.
is open.
-
(V)
The UGIVEP has a solution. By Lemma 1.6,
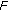 has a fixed point. Thus, there exists
has a fixed point. Thus, there exists  such that
such that 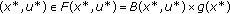 , that is,
, that is, 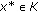 and
and 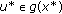 such that
such that  and
and

This completes the proof.
References
Li J, Huang N-J, Kim JK: On implicit vector equilibrium problems. Journal of Mathematical Analysis and Applications 2003,283(2):501–512. 10.1016/S0022-247X(03)00277-4
Konnov IV, Yao JC: Existence of solutions for generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 1999,233(1):328–335. 10.1006/jmaa.1999.6312
Ceng L-C, Guu S-M, Yao J-C: On generalized implicit vector equilibrium problems in Banach spaces. Computers & Mathematics with Applications 2009,57(10):1682–1691. 10.1016/j.camwa.2009.02.026
Chen XH: Existence of solution for the implicit multi-valued vector equilibrium problem. Journal of Applied Mathematics and Computing 2009,30(1–2):469–478. 10.1007/s12190-008-0186-5
Huang NJ, Li J, Thompson HB: Implicit vector equilibrium problems with applications. Mathematical and Computer Modelling 2003,37(12–13):1343–1356. 10.1016/S0895-7177(03)90045-8
Li J, Huang N-J: Implicit vector equilibrium problems via nonlinear scalarisation. Bulletin of the Australian Mathematical Society 2005,72(1):161–172. 10.1017/S000497270003495X
Chen G-Y, Huang XX, Yang XQ: Vector Optimization: Set-Valued and Variational Analysis, Lecture Notes in Economics and Mathematical Systems. Volume 541. Springer, Berlin, Germany; 2005.
Horvath CD, Llinares Ciscar JV: Maximal elements and fixed points for binary relations on topological ordered spaces. Journal of Mathematical Economics 1996,25(3):291–306. 10.1016/0304-4068(95)00732-6
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1984.
Luo Q: Ky Fan's section theorem and its applications in topological ordered spaces. Applied Mathematics Letters 2004,17(10):1113–1119. 10.1016/j.aml.2003.12.003
Acknowledgments
This research was supported by the Natural Science Foundations of Guangdong Province (9251064101000015). The author is grateful to the referees for the valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Luo, Q. On Generalized Implicit Vector Equilibrium Problems in Topological Ordered Spaces. Fixed Point Theory Appl 2009, 513408 (2009). https://doi.org/10.1155/2009/513408
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/513408
 ,
,  is
is  -concave with respect to
-concave with respect to  ;
;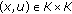 ,
, 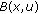 is nonempty.
is nonempty. ,
,  is
is 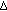 -convex. If it is false, then there exists
-convex. If it is false, then there exists 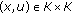 such that
such that  is not
is not  -convex, that is, there exist
-convex, that is, there exist  such that
such that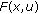 is nonempty
is nonempty 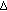 -convex for any
-convex for any 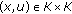 . By steps (I) and (II), the conclusion follows directly from
. By steps (I) and (II), the conclusion follows directly from 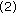 .
.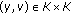 ,
,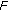 has a fixed point. Thus, there exists
has a fixed point. Thus, there exists  such that
such that 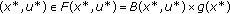 , that is,
, that is, 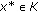 and
and 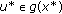 such that
such that  and
and