- Research Article
- Open access
- Published:
Common Fixed Point and Approximation Results for Noncommuting Maps on Locally Convex Spaces
Fixed Point Theory and Applications volume 2009, Article number: 207503 (2009)
Abstract
Common fixed point results for some new classes of nonlinear noncommuting maps on a locally convex space are proved. As applications, related invariant approximation results are obtained. Our work includes improvements and extension of several recent developments of the existing literature on common fixed points. We also provide illustrative examples to demonstrate the generality of our results over the known ones.
1. Introduction and Preliminaries
In the sequel,  will be a Hausdorff locally convex topological vector space. A family
will be a Hausdorff locally convex topological vector space. A family  of seminorms defined on
of seminorms defined on  is said to be an associated family of seminorms for
is said to be an associated family of seminorms for  if the family
if the family  where
where  and
and  , forms a base of neighborhoods of zero for
, forms a base of neighborhoods of zero for  . A family
. A family  of seminorms defined on
of seminorms defined on  is called an augmented associated family for
is called an augmented associated family for  if
if  is an associated family with property that the seminorm
is an associated family with property that the seminorm  for any
for any  . The associated and augmented associated families of seminorms will be denoted by
. The associated and augmented associated families of seminorms will be denoted by  and
and  , respectively. It is well known that given a locally convex space
, respectively. It is well known that given a locally convex space  there always exists a family
there always exists a family  of seminorms defined on
of seminorms defined on  such that
such that  (see [1, page 203]).
(see [1, page 203]).
The following construction will be crucial. Suppose that  is a
is a  -bounded subset of
-bounded subset of  . For this set
. For this set  we can select a number
we can select a number  for each
for each  such that
such that  where
where  Clearly,
Clearly,  is
is  -bounded,
-bounded,  -closed, absolutely convex and contains
-closed, absolutely convex and contains  . The linear span
. The linear span  of
of  in
in  is
is  The Minkowski functional of
The Minkowski functional of  is a norm
is a norm  on
on  . Thus
. Thus  is a normed space with
is a normed space with  as its closed unit ball and
as its closed unit ball and  for each
for each  (for details see [1–3]).
(for details see [1–3]).
Let  be a subset of a locally convex space
be a subset of a locally convex space  . Let
. Let  be mappings. A mapping
be mappings. A mapping  is called
is called  -Lipschitz if there exists
-Lipschitz if there exists  such that
such that  for any
for any  and for all
and for all  . If
. If  (resp.,
(resp.,  ), then
), then  is called an
is called an  -contraction (resp.,
-contraction (resp.,  -nonexpansive). A point
-nonexpansive). A point  is a common fixed (coincidence) point of
is a common fixed (coincidence) point of  and
and  if
if  (
( ). The set of coincidence points of
). The set of coincidence points of  and
and  is denoted by
is denoted by  and the set of fixed points of
and the set of fixed points of  is denoted by
is denoted by  The pair
The pair  is called:
is called:
(1)commuting if  for all
for all  ;
;
(2) -weakly commuting if for all
-weakly commuting if for all  and for all
and for all  , there exists
, there exists  such that
such that  If
If  , then the maps are called weakly commuting [4];
, then the maps are called weakly commuting [4];
(3)compatible [5] if for all  ,
,  whenever
whenever  is a sequence such that
is a sequence such that  for some
for some  in
in  ;
;
(4)weakly compatible if they commute at their coincidence points, that is,  whenever
whenever  .
.
Suppose that  is
is  -starshaped with
-starshaped with  and is both
and is both  - and
- and  -invariant. Then
-invariant. Then  and
and  are called:
are called:
(5) -subcommuting on
-subcommuting on  if for all
if for all  and for all
and for all  , there exists a real number
, there exists a real number  such that
such that  for each
for each  . If
. If  , then the maps are called
, then the maps are called  -subcommuting [6];
-subcommuting [6];
(6) -subweakly commuting on
-subweakly commuting on  (see [7]) if for all
(see [7]) if for all  and for all
and for all  , there exists a real number
, there exists a real number  such that
such that  , where
, where  and
and  ;
;
(7) -commuting [8, 9] if
-commuting [8, 9] if  for all
for all  , where
, where  and
and  .
.
If  then we define the set,
then we define the set,  , of best
, of best  -approximations to
-approximations to  as
as  , for all
, for all  . A mapping
. A mapping  is called demiclosed at
is called demiclosed at  if
if  converges weakly to
converges weakly to  and
and  converges to
converges to  , then we have
, then we have  . A locally convex space
. A locally convex space  satisfies Opial's condition if for every net
satisfies Opial's condition if for every net  in
in  weakly convergent to
weakly convergent to  the inequality
the inequality

holds for all  and
and  .
.
In 1963, Meinardus [10] employed the Schauder fixed point theorem to prove a result regarding invariant approximation. Singh [11], Sahab et al. [12], and Jungck and Sessa [13] proved similar results in best approximation theory. Recently, Hussain and Khan [6] have proved more general invariant approximation results for 1-subcommuting maps which extend the work of Jungck and Sessa [13] and Al-Thagafi [14] to locally convex spaces. More recently, with the introduction of noncommuting maps to this area, Pant [15], Pathak et al. [16], Hussain and Jungck [7], and Jungck and Hussain [9] further extended and improved the above-mentioned results; details on the subject may be found in [17, 18]. For applications of fixed point results of nonlinear mappings in simultaneous best approximation theory and variational inequalities, we refer the reader to [19–21]. Fixed point theory of nonexpansive and noncommuting mappings is very rich in Banach spaces and metric spaces [13–17]. However, some partial results have been obtained for these mappings in the setup of locally convex spaces (see [22] and its references). It is remarked that the generalization of a known result in Banach space setting to the case of locally convex spaces is neither trivial nor easy (see, e.g., [2, 22]).
The following general common fixed point result is a consequence of Theorem 3.1 of Jungck [5], which will be needed in the sequel.
Theorem 1.1.
Let  be a complete metric space, and let
be a complete metric space, and let  be selfmaps of
be selfmaps of  . Suppose that
. Suppose that  and
and  are continuous, the pairs
are continuous, the pairs  and
and  are compatible such that
are compatible such that  . If there exists
. If there exists  such that for all
such that for all 

then there is a unique point  in
in  such that
such that  .
.
The aim of this paper is to extend the above well-known result of Jungck to locally convex spaces and establish general common fixed point theorems for generalized  -nonexpansive subcompatible maps in the setting of a locally convex space. We apply our theorems to derive some results on the existence of common fixed points from the set of best approximations. We also establish common fixed point and approximation results for the newly defined class of Banach operator pairs. Our results extend and unify the work of Al-Thagafi [14], Chen and Li [23], Hussain [24], Hussain and Berinde [25], Hussain and Jungck [7], Hussain and Khan [6], Hussain and Rhoades [8], Jungck and Sessa [13], Khan and Akbar [19, 20], Pathak and Hussain [21], Sahab et al. [12], Sahney et al. [26], Singh [11, 27], Tarafdar [3], and Taylor [28].
-nonexpansive subcompatible maps in the setting of a locally convex space. We apply our theorems to derive some results on the existence of common fixed points from the set of best approximations. We also establish common fixed point and approximation results for the newly defined class of Banach operator pairs. Our results extend and unify the work of Al-Thagafi [14], Chen and Li [23], Hussain [24], Hussain and Berinde [25], Hussain and Jungck [7], Hussain and Khan [6], Hussain and Rhoades [8], Jungck and Sessa [13], Khan and Akbar [19, 20], Pathak and Hussain [21], Sahab et al. [12], Sahney et al. [26], Singh [11, 27], Tarafdar [3], and Taylor [28].
2. Subcompatible Maps in Locally Convex Spaces
Recently, Khan et al. [29] introduced the class of subcompatible mappings as follows:
Definition 2.1.
Let  be a
be a  -starshaped subset of a normed space
-starshaped subset of a normed space  . For the selfmaps
. For the selfmaps  and
and  of
of  with
with  we define
we define  where
where  and
and  . Now
. Now  and
and  are subcompatible if
are subcompatible if  for all sequences
for all sequences  .
.
We can extend this definition to a locally convex space by replacing the norm with a family of seminorms.
Clearly, subcompatible maps are compatible but the converse does not hold, in general, as the following example shows.
Example 2.2 (see [29]).
Let  with usual norm and
with usual norm and  Let
Let  and
and  for all
for all  . Let
. Let  Then
Then  is
is  -starshaped with
-starshaped with  . Note that
. Note that  and
and  are compatible. For any sequence
are compatible. For any sequence  in
in  with
with  , we have,
, we have,  . However,
. However,  . Thus
. Thus  and
and  are not subcompatible maps.
are not subcompatible maps.
Note that  -subweakly commuting and
-subweakly commuting and  -subcommuting maps are subcompatible. The following simple example reveals that the converse is not true, in general.
-subcommuting maps are subcompatible. The following simple example reveals that the converse is not true, in general.
Example 2.3 (see [29]).
Let  with usual norm and
with usual norm and  Let
Let  if
if  and
and  if
if  , and
, and  if
if  and
and  if
if  . Then
. Then  is
is  -starshaped with
-starshaped with  and
and  . Note that
. Note that  and
and  are subcompatible but not
are subcompatible but not  -weakly commuting for all
-weakly commuting for all  . Thus
. Thus  and
and  are neither
are neither  -subweakly commuting nor
-subweakly commuting nor  -subcommuting maps.
-subcommuting maps.
We observe in the following example that the weak commutativity of a pair of selfmaps on a metric space depends on the choice of the metric; this is also true for compatibility,  -weak commutativity, and other variants of commutativity of maps.
-weak commutativity, and other variants of commutativity of maps.
Example 2.4 (see [30]).
Let  with usual metric and
with usual metric and  Let
Let  and
and  . Then
. Then  and
and  . Thus the pair
. Thus the pair  is not weakly commuting on
is not weakly commuting on  with respect to usual metric. But if
with respect to usual metric. But if  is endowed with the discrete metric
is endowed with the discrete metric  , then
, then  for
for  . Thus the pair
. Thus the pair  is weakly commuting on
is weakly commuting on  with respect to discrete metric.
with respect to discrete metric.
Next we establish a positive result in this direction in the context of linear topologies utilizing Minkowski functional; it extends [6, Lemma 2.1].
Lemma 2.5.
Let  and
and  be compatible selfmaps of a
be compatible selfmaps of a  -bounded subset
-bounded subset  of a Hausdorff locally convex space
of a Hausdorff locally convex space  . Then
. Then  and
and  are compatible on
are compatible on  with respect to
with respect to 
Proof.
By hypothesis,  for each
for each  whenever
whenever  for some
for some  . Taking supremum on both sides, we get
. Taking supremum on both sides, we get

whenever

This implies that

whenever

Hence  whenever
whenever  as desired.
as desired.
There are plenty of spaces which are not normable (see [31, page 113]). So it is natural and essential to consider fixed point and approximation results in the context of a locally convex space. An application of Lemma 2.5 provides the following general common fixed point result.
Theorem 2.6.
Let  be a nonempty
be a nonempty  -bounded,
-bounded,  -complete subset of a Hausdorff locally convex space
-complete subset of a Hausdorff locally convex space  and let
and let  and
and  be selfmaps of
be selfmaps of  Suppose that
Suppose that  and
and  are nonexpansive, the pairs
are nonexpansive, the pairs  and
and  are compatible such that
are compatible such that  . If there exists
. If there exists  such that for all
such that for all  and for all
and for all 

then there is a unique point  in
in  such that
such that  .
.
Proof.
Since the norm topology on  has a base of neighbourhoods of
has a base of neighbourhoods of  consisting of
consisting of  -closed sets and
-closed sets and  is
is  -sequentially complete, therefore
-sequentially complete, therefore  is
is  - sequentially complete in
- sequentially complete in  see [3, the proof of Theorem 1.2]. By Lemma 2.5, the pairs
see [3, the proof of Theorem 1.2]. By Lemma 2.5, the pairs  and
and  are
are  compatible maps of
compatible maps of  . From (2.5) we obtain for any
. From (2.5) we obtain for any  ,
,

Thus

As  and
and  are nonexpansive on
are nonexpansive on  -bounded set
-bounded set  ,
,  and
and  are also nonexpansive with respect to
are also nonexpansive with respect to  and hence continuous (cf. [6]). A comparison of our hypothesis with that of Theorem 1.1 tells that we can apply Theorem 1.1 to
and hence continuous (cf. [6]). A comparison of our hypothesis with that of Theorem 1.1 tells that we can apply Theorem 1.1 to  as a subset of
as a subset of  to conclude that there exists a unique
to conclude that there exists a unique  in
in  such that
such that  .
.
We now prove the main result of this section.
Theorem 2.7.
Let  be a nonempty
be a nonempty  -bounded,
-bounded,  -sequentially complete,
-sequentially complete,  -starshaped subset of a Hausdorff locally convex space
-starshaped subset of a Hausdorff locally convex space  and let
and let  and
and  be selfmaps of
be selfmaps of  Suppose that
Suppose that  and
and  are affine and nonexpansive with
are affine and nonexpansive with  , and
, and  . If the pairs
. If the pairs  and
and  are subcompatible and, for all
are subcompatible and, for all  and for all
and for all 

then  provided that one of the following conditions holds:
provided that one of the following conditions holds:
(i) is
is  -sequentially compact, and
-sequentially compact, and  is continuous (
is continuous ( stands for closure);
stands for closure);
(ii) is
is  -sequentially compact, and
-sequentially compact, and  is continuous;
is continuous;
(iii) is weakly compact in
is weakly compact in  and
and  is demiclosed at
is demiclosed at  .
.
Proof.
Define  by
by

for all  and a fixed sequence of real numbers
and a fixed sequence of real numbers  ) converging to
) converging to  . Then, each
. Then, each  is a selfmap of
is a selfmap of  and for each
and for each  ,
,  since
since  and
and  are affine and
are affine and  As
As  is affine and the pair
is affine and the pair  is subcompatible, so for any
is subcompatible, so for any  with
with  , we have
, we have

Thus the pair  is compatible on
is compatible on  for each
for each  . Similarly, the pair
. Similarly, the pair  is compatible for each
is compatible for each  .
.
Also by (2.8),

for each  ,
,  and
and  . By Theorem 2.6, for each
. By Theorem 2.6, for each  , there exists
, there exists  such that
such that  .
.
-
(i)
The compactness of
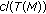 implies that there exists a subsequence
implies that there exists a subsequence 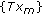 of
of 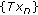 and a
and a 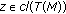 such that
such that 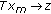 as
as  . Since
. Since  ,
, 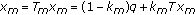 also converges to
also converges to 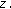 Since
Since  ,
, 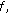 and
and 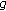 are continuous, we have
are continuous, we have 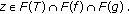 Thus
Thus 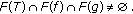
-
(ii)
Proof follows from (i).
-
(iii)
Since
 is weakly compact, there is a subsequence
is weakly compact, there is a subsequence  of
of  converging weakly to some
converging weakly to some  . But,
. But,  and
and  being affine and continuous are weakly continuous, and the weak topology is Hausdorff, so we have
being affine and continuous are weakly continuous, and the weak topology is Hausdorff, so we have 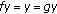 . The set
. The set 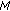 is bounded, so
is bounded, so  as
as  Now the demiclosedness of
Now the demiclosedness of 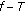 at
at  guarantees that
guarantees that 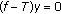 and hence
and hence 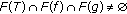 .
.
Theorem 2.7 extends and improves [14, Theorem 2.2], [7, Theorems 2.2-2.3, and Corollaries 2.4–2.7], [13, Theorem 6], and the main results of Tarafdar [3] and Taylor [28](see also [6, Remarks 2.4]).
Theorem 2.8.
Let  be a nonempty
be a nonempty  -bounded,
-bounded,  -sequentially complete,
-sequentially complete,  -starshaped subset of a Hausdorff locally convex space
-starshaped subset of a Hausdorff locally convex space  and let
and let  and
and  be selfmaps of
be selfmaps of  Suppose that
Suppose that  and
and  are affine and nonexpansive with
are affine and nonexpansive with  , and
, and  . If the pairs
. If the pairs  and
and  are subcompatible and
are subcompatible and  is
is  -nonexpansive, then
-nonexpansive, then  provided that one of the following conditions holds
provided that one of the following conditions holds
(i) is
is  -sequentially compact;
-sequentially compact;
(ii) is
is  -sequentially compact;
-sequentially compact;
(iii) is weakly compact in
is weakly compact in  ,
,  is demiclosed at
is demiclosed at  .
.
(iv) is weakly compact in an Opial space
is weakly compact in an Opial space  .
.
Proof.
(i)–(iii) follow from Theorem 2.7.
-
(iv)
As in (iii) we have
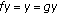 and
and  as
as 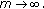 If
If 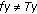 , then by the Opial's condition of
, then by the Opial's condition of 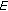 and
and 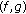 -nonexpansiveness of
-nonexpansiveness of 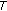 we get,
we get,  (2.12)
(2.12)
which is a contradiction. Thus  and hence
and hence  .
.
As  -subcommuting maps are subcompatible, so by Theorem 2.8, we obtain the following recent result of Hussain and Khan [6] without the surjectivity of
-subcommuting maps are subcompatible, so by Theorem 2.8, we obtain the following recent result of Hussain and Khan [6] without the surjectivity of  . Note that a continuous and affine map is weakly continuous, so the weak continuity of
. Note that a continuous and affine map is weakly continuous, so the weak continuity of  is not required as well.
is not required as well.
Corollary 2.9 ([6, Theorem 2.2]).
Let  be a nonempty
be a nonempty  -bounded,
-bounded,  -sequentially complete,
-sequentially complete,  -starshaped subset of a Hausdorff locally convex space
-starshaped subset of a Hausdorff locally convex space  and let
and let  be selfmaps of
be selfmaps of  Suppose that
Suppose that  is affine and nonexpansive with
is affine and nonexpansive with  , and
, and  . If the pair
. If the pair  is
is  -subcommuting and
-subcommuting and  is
is  -nonexpansive, then
-nonexpansive, then  provided that one of the following conditions holds:
provided that one of the following conditions holds:
(i) is
is  -sequentially compact;
-sequentially compact;
(ii) is
is  -sequentially compact;
-sequentially compact;
(iii) is weakly compact in
is weakly compact in  ,
,  is demiclosed at
is demiclosed at  .
.
(iv) is weakly compact in an Opial space
is weakly compact in an Opial space  .
.
The following theorem improves and extends the corresponding approximation results in [6–8, 11–14, 25, 27].
Theorem 2.10.
Let  be a nonempty subset of a Hausdorff locally convex space
be a nonempty subset of a Hausdorff locally convex space  and let
and let  be mappings such that
be mappings such that  for some
for some  and
and  . Suppose that
. Suppose that  and
and  are affine and nonexpansive on
are affine and nonexpansive on  with
with  is
is  -bounded,
-bounded,  -sequentially complete,
-sequentially complete,  -starshaped and
-starshaped and  . If the pairs
. If the pairs  and
and  are subcompatible and, for all
are subcompatible and, for all  and
and  ,
,

then  , provided that one of the following conditions holds
, provided that one of the following conditions holds
(i) is
is  -sequentially compact, and
-sequentially compact, and  is continuous;
is continuous;
(ii) is
is  -sequentially compact, and
-sequentially compact, and  is continuous;
is continuous;
(iii) is weakly compact, and
is weakly compact, and  is demiclosed at
is demiclosed at  .
.
Proof.
Let  . Then for each
. Then for each  ,
,  . Note that for any
. Note that for any  ,
, 
It follows that the line segment  and the set
and the set  are disjoint. Thus
are disjoint. Thus  is not in the interior of
is not in the interior of  and so
and so  . Since
. Since  ,
,  must be in
must be in  . Also since
. Also since  ,
,  and
and  satisfy (2.13), we have for each
satisfy (2.13), we have for each  ,
,

Thus  Consequently,
Consequently,  . Now Theorem 2.7 guarantees that
. Now Theorem 2.7 guarantees that  .
.
Remark 2.11.
One can now easily prove on the lines of the proof of the above theorem that the approximation results are similar to those of Theorems 2.11-2.12 due to Hussain and Jungck [7] in the setting of a Hausdorff locally convex space.
We define  and denote by
and denote by  the class of closed convex subsets of
the class of closed convex subsets of  containing
containing  . For
. For  , we define
, we define  for each
for each  . It is clear that
. It is clear that  .
.
The following result extends [14, Theorem 4.1] and [7, Theorem 2.14].
Theorem 2.12.
Let  be selfmaps of a Hausdorff locally convex space
be selfmaps of a Hausdorff locally convex space  with
with  and
and  such that
such that  . Suppose that
. Suppose that  and
and  for all
for all  and for each
and for each  where
where  is compact. Then
is compact. Then
(i) is nonempty, closed, and convex,
is nonempty, closed, and convex,
(ii)
(iii) provided
provided  and
and  are subcompatible, affine, and nonexpansive on
are subcompatible, affine, and nonexpansive on  , and, for some
, and, for some  and for all
and for all 

 is continuous, the pairs
is continuous, the pairs  and
and  are subcompatible on
are subcompatible on  and satisfy for all
and satisfy for all 

for all  and for each
and for each  .
.
Proof.
Then there is a minimizing sequence  in
in  such that
such that  As
As  is compact so
is compact so  has a convergent subsequence
has a convergent subsequence  with
with  (say) in
(say) in  Now by using
Now by using

we get for each  ,
,

Hence  Thus
Thus  is nonempty closed and convex.
is nonempty closed and convex.
(i)Follows from [7, Theorem 2.14].
(ii)By Theorem 2.7(i),  so it follows that there exists
so it follows that there exists  such that
such that  Hence (iii) follows from Theorem 2.7(i).
Hence (iii) follows from Theorem 2.7(i).
3. Banach Operator Pair in Locally Convex Spaces
Utilizing similar arguments as above, the following result can be proved which extends recent common fixed point results due to Hussain and Rhoades [8, Theorem 2.1] and Jungck and Hussain [9, Theorem 2.1] to the setup of a Hausdorff locally convex space which is not necessarily metrizable.
Theorem 3.1.
Let  be a
be a  -bounded subset of a Hausdorff locally convex space
-bounded subset of a Hausdorff locally convex space  , and let
, and let  and let
and let  be weakly compatible self-maps of
be weakly compatible self-maps of  . Assume that
. Assume that  ,
,  is
is  -sequentially complete, and
-sequentially complete, and  and
and  satisfy, for all
satisfy, for all  ,
,  and for some
and for some 

Then  is a singleton.
is a singleton.
As an application of Theorem 3.1, the analogue of all the results due to Hussain and Berinde [25], and Hussain and Rhoades [8] can be established for  -commuting maps
-commuting maps  and
and  defined on a
defined on a  -bounded subset
-bounded subset  of a Hausdorff locally convex space. We leave details to the reader.
of a Hausdorff locally convex space. We leave details to the reader.
Recently, Chen and Li [23] introduced the class of Banach operator pairs, as a new class of noncommuting maps and it has been further studied by Hussain [24], Ciric et al. [32], Khan and Akbar [19, 20], and Pathak and Hussain [21]. The pair  is called a Banach operator pair, if the set
is called a Banach operator pair, if the set  is
is  -invariant, namely,
-invariant, namely,  . Obviously, commuting pair
. Obviously, commuting pair  is a Banach operator pair but converse is not true, in general; see [21, 23]. If
is a Banach operator pair but converse is not true, in general; see [21, 23]. If  is a Banach operator pair, then
is a Banach operator pair, then  need not be a Banach operator pair (cf. [23, Example 1]).
need not be a Banach operator pair (cf. [23, Example 1]).
Chen and Li [23] proved the following.
Theorem 3.2 ([23, Theorems 3.2-3.3]).
Let  be a
be a  -starshaped subset of a normed space
-starshaped subset of a normed space  and let
and let  ,
,  be self-mappings of
be self-mappings of  Suppose that
Suppose that  is
is  -starshaped and
-starshaped and  is continuous on
is continuous on  . If
. If  is compact (resp.,
is compact (resp.,  is weakly continuous,
is weakly continuous,  is complete,
is complete,  is weakly compact, and either
is weakly compact, and either  is demiclosed at
is demiclosed at  or
or  satisfies Opial's condition),
satisfies Opial's condition),  is a Banach operator pair, and
is a Banach operator pair, and  is
is  -nonexpansive on
-nonexpansive on  , then
, then  .
.
In this section, we extend and improve the above-mentioned common fixed point results of Chen and Li [23] in the setup of a Hausdorff locally convex space.
Lemma 3.3.
Let  be a nonempty
be a nonempty  -bounded subset of Hausdorff locally convex space
-bounded subset of Hausdorff locally convex space  , and let
, and let  and
and  be self-maps of
be self-maps of  If
If  is nonempty,
is nonempty,  ,
,  is
is  -sequentially complete, and
-sequentially complete, and  ,
,  and
and  satisfy for all
satisfy for all  and for some
and for some 

then  is singleton.
is singleton.
Proof.
Note that  being a subset of
being a subset of  is
is  -sequentially complete. Further, for all
-sequentially complete. Further, for all  , we have
, we have

Hence  is a generalized contraction on
is a generalized contraction on  and
and  . By Theorem 3.1 (with
. By Theorem 3.1 (with  = identity map),
= identity map),  has a unique fixed point
has a unique fixed point  in
in  and consequently,
and consequently,  is singleton.
is singleton.
The following result generalizes [19, Theorem 2.3], [24, Theorem 2.11], and [21, Theorem 2.2] and improves [14, Theorem 2.2] and [13, Theorem 6].
Theorem 3.4.
Let  be a nonempty
be a nonempty  -bounded subset of Hausdorff locally convex (resp., complete) space
-bounded subset of Hausdorff locally convex (resp., complete) space  and let
and let  and
and  be self-maps of
be self-maps of  Suppose that
Suppose that  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact (resp.,
is compact (resp.,  is weakly compact),
is weakly compact),  is continuous on
is continuous on  (resp.,
(resp.,  is demiclosed at
is demiclosed at  , where
, where  stands for identity map) and
stands for identity map) and

For all  then
then  .
.
Proof.
Define  by
by  for all
for all  and a fixed sequence of real numbers
and a fixed sequence of real numbers  ) converging to
) converging to  . Since
. Since  is
is  -starshaped and
-starshaped and  (resp.,
(resp.,  ), so
), so  ) (resp.,
) (resp.,  ) for each
) for each  . Also by (3.4)
. Also by (3.4)

for each  and some
and some 
If  is compact, for each
is compact, for each  ,
,  is
is  -compact and hence
-compact and hence  -sequentially complete. By Lemma 3.3, for each
-sequentially complete. By Lemma 3.3, for each  there exists
there exists  such that
such that  The compactness of
The compactness of  implies that there exists a subsequence
implies that there exists a subsequence  of
of  such that
such that  as
as  . Since
. Since  is a sequence in
is a sequence in  and
and  , therefore
, therefore  . Further,
. Further,  . By the continuity of
. By the continuity of  , we obtain
, we obtain  . Thus,
. Thus,  proves the first case.
proves the first case.
The weak compactness of  implies that
implies that  is weakly compact and hence
is weakly compact and hence  -sequentially complete due to completeness of
-sequentially complete due to completeness of  . From Lemma 3.3, for each
. From Lemma 3.3, for each  there exists
there exists  such that
such that  Moreover, we have
Moreover, we have  as
as  . The weak compactness of
. The weak compactness of  implies that there is a subsequence
implies that there is a subsequence  of
of  converging weakly to
converging weakly to  as
as  . Since
. Since  is a sequence in
is a sequence in  , therefore
, therefore  . Also we have,
. Also we have,  as
as  . If
. If  is demiclosed at
is demiclosed at  , then
, then  . Thus
. Thus 
Corollary 3.5.
Let  be a nonempty
be a nonempty  -bounded subset of Hausdorff locally convex (resp., complete) space
-bounded subset of Hausdorff locally convex (resp., complete) space  and let
and let  and
and  be self-maps of
be self-maps of  Suppose that
Suppose that  is
is  -starshaped, and
-starshaped, and  -closed (resp.,
-closed (resp.,  -weakly closed),
-weakly closed),  is compact (resp.,
is compact (resp.,  is weakly compact),
is weakly compact),  is continuous on
is continuous on  (resp.,
(resp.,  is demiclosed at
is demiclosed at  ),
),  and
and  are Banach operator pairs and satisfy (3.4) for all
are Banach operator pairs and satisfy (3.4) for all  then
then  .
.
Let  where
where  and
and  It is important to note here that
It is important to note here that  is always bounded.
is always bounded.
Corollary 3.6.
Let  be a Hausdorff locally convex (resp., complete) space and
be a Hausdorff locally convex (resp., complete) space and  and
and  be self-maps of
be self-maps of  If
If  ,
,  ,
,  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ],
],  is compact (resp.,
is compact (resp.,  is weakly compact),
is weakly compact),  is continuous on
is continuous on  (resp.,
(resp.,  is demiclosed at
is demiclosed at  ), and (3.4) holds for all
), and (3.4) holds for all  then
then  .
.
Corollary 3.7.
Let  be a Hausdorff locally convex (resp., complete) space and
be a Hausdorff locally convex (resp., complete) space and  and
and  be self-maps of
be self-maps of  If
If  ,
,  ,
,  is
is  -starshaped,
-starshaped,  (resp.,
(resp.,  ),
),  is compact (resp.,
is compact (resp.,  is weakly compact),
is weakly compact),  is continuous on
is continuous on  (resp.,
(resp.,  is demiclosed at
is demiclosed at  ), and (3.4) holds for all
), and (3.4) holds for all  then
then  .
.
Remark 3.8.
Khan and Akbar [19, Corollaries 2.4–2.8] and Chen and Li [23, Theorems 4.1 and 4.2] are particular cases of Corollaries 3.5 and 3.6.
The following result extends [14, Theorem 4.1], [7, Theorem 2.14], [19, Theorem 2.9], and [21, Theorems 2.7–2.11].
Theorem 3.9.
Let  be self-maps of a Hausdorff locally convex space
be self-maps of a Hausdorff locally convex space  . If
. If  and
and  such that
such that  ,
,  is compact and
is compact and  for all
for all  , then
, then  is nonempty, closed, and convex with
is nonempty, closed, and convex with  . If, in addition,
. If, in addition,  ,
,  is
is  -starshaped,
-starshaped,  ,
,  is continuous on
is continuous on  and (3.4) holds for all
and (3.4) holds for all  then
then  .
.
Proof.
We utilize Corollary 3.5 instead of Theorem 2.7 in the proof of Theorem 2.12.
Remark 3.10.
References
Köthe G: Topological Vector Spaces. I, Die Grundlehren der mathematischen Wissenschaften. Volume 159. Springer, New York, NY, USA; 1969:xv+456.
Cheng LX, Zhou Y, Zhang F: Danes' drop theorem in locally convex spaces. Proceedings of the American Mathematical Society 1996,124(12):3699–3702. 10.1090/S0002-9939-96-03404-1
Tarafdar E: Some fixed-point theorems on locally convex linear topological spaces. Bulletin of the Australian Mathematical Society 1975,13(2):241–254. 10.1017/S0004972700024436
Sessa S: On a weak commutativity condition of mappings in fixed point considerations. Publications de l'Institut Mathématique 1982, 32(46): 149–153.
Jungck G: Common fixed points for commuting and compatible maps on compacta. Proceedings of the American Mathematical Society 1988,103(3):977–983. 10.1090/S0002-9939-1988-0947693-2
Hussain N, Khan AR: Common fixed-point results in best approximation theory. Applied Mathematics Letters 2003,16(4):575–580. 10.1016/S0893-9659(03)00039-9
Hussain N, Jungck G: Common fixed point and invariant approximation results for noncommuting generalized -nonexpansive maps. Journal of Mathematical Analysis and Applications 2006,321(2):851–861. 10.1016/j.jmaa.2005.08.045
Hussain N, Rhoades BE: -commuting maps and invariant approximations. Fixed Point Theory and Applications 2006, Article ID 24543, 2006:-9.
Jungck G, Hussain N: Compatible maps and invariant approximations. Journal of Mathematical Analysis and Applications 2007,325(2):1003–1012. 10.1016/j.jmaa.2006.02.058
Meinardus G: Invarianz bei linearen Approximationen. Archive for Rational Mechanics and Analysis 1963,14(1):301–303.
Singh SP: An application of a fixed-point theorem to approximation theory. Journal of Approximation Theory 1979,25(1):89–90. 10.1016/0021-9045(79)90036-4
Sahab SA, Khan MS, Sessa S: A result in best approximation theory. Journal of Approximation Theory 1988,55(3):349–351. 10.1016/0021-9045(88)90101-3
Jungck G, Sessa S: Fixed point theorems in best approximation theory. Mathematica Japonica 1995,42(2):249–252.
Al-Thagafi MA: Common fixed points and best approximation. Journal of Approximation Theory 1996,85(3):318–323. 10.1006/jath.1996.0045
Pant RP: Common fixed points of noncommuting mappings. Journal of Mathematical Analysis and Applications 1994,188(2):436–440. 10.1006/jmaa.1994.1437
Pathak HK, Cho YJ, Kang SM: Remarks on -weakly commuting mappings and common fixed point theorems. Bulletin of the Korean Mathematical Society 1997,34(2):247–257.
Khamsi MA, Kirk WA: An Introduction to Metric Spaces and Fixed Point Theory, Pure and Applied Mathematics. Wiley-Interscience, New York, NY, USA; 2001:x+302.
Singh S, Watson B, Srivastava P: Fixed Point Theory and Best Approximation: The KKM-Map Principle, Mathematics and Its Applications. Volume 424. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:x+220.
Khan AR, Akbar F: Best simultaneous approximations, asymptotically nonexpansive mappings and variational inequalities in Banach spaces. Journal of Mathematical Analysis and Applications 2009,354(2):469–477. 10.1016/j.jmaa.2009.01.007
Khan AR, Akbar F: Common fixed points from best simultaneous approximations. Taiwanese Journal of Mathematics 2009.,13(4):
Pathak HK, Hussain N: Common fixed points for Banach operator pairs with applications. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):2788–2802. 10.1016/j.na.2007.08.051
Cain GL Jr., Nashed MZ: Fixed points and stability for a sum of two operators in locally convex spaces. Pacific Journal of Mathematics 1971, 39: 581–592.
Chen J, Li Z: Common fixed-points for Banach operator pairs in best approximation. Journal of Mathematical Analysis and Applications 2007,336(2):1466–1475. 10.1016/j.jmaa.2007.01.064
Hussain N: Common fixed points in best approximation for Banach operator pairs with Ćirić type -contractions. Journal of Mathematical Analysis and Applications 2008,338(2):1351–1363. 10.1016/j.jmaa.2007.06.008
Hussain N, Berinde V: Common fixed point and invariant approximation results in certain metrizable topological vector spaces. Fixed Point Theory and Applications 2006, Article ID 23582, 2006:-13.
Sahney BN, Singh KL, Whitfield JHM: Best approximations in locally convex spaces. Journal of Approximation Theory 1983,38(2):182–187. 10.1016/0021-9045(83)90125-9
Singh SP: Some results on best approximation in locally convex spaces. Journal of Approximation Theory 1980,28(4):329–332. 10.1016/0021-9045(80)90067-2
Taylor WW: Fixed-point theorems for nonexpansive mappings in linear topological spaces. Journal of Mathematical Analysis and Applications 1972,40(1):164–173. 10.1016/0022-247X(72)90040-6
Khan AR, Akbar F, Sultana N: Random coincidence points of subcompatible multivalued maps with applications. Carpathian Journal of Mathematics 2008,24(2):63–71.
Singh SL, Tomar A: Weaker forms of commuting maps and existence of fixed points. Journal of the Korea Society of Mathematical Education. Series B 2003,10(3):145–161.
Fabian M, Habala P, Hájek P, Montesinos Santalucía V, Pelant J, Zizler V: Functional Analysis and Infinite-Dimensional Geometry, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, 8. Springer, New York, NY, USA; 2001:x+451.
Ćirić LB, Husain N, Akbar F, Ume JS: Common fixed points for Banach operator pairs from the set of best approximations. Bulletin of the Belgian Mathematical Society. Simon Stevin 2009., 16:
Acknowledgments
The author A. R. Khan gratefully acknowledges the support provided by the King Fahd University of Petroleum & Minerals during this research. The authors would like to thank the referees for their valuable suggestions to improve the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Akbar, F., Khan, A.R. Common Fixed Point and Approximation Results for Noncommuting Maps on Locally Convex Spaces. Fixed Point Theory Appl 2009, 207503 (2009). https://doi.org/10.1155/2009/207503
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/207503
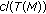 implies that there exists a subsequence
implies that there exists a subsequence 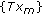 of
of 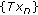 and a
and a 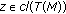 such that
such that 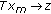 as
as  . Since
. Since  ,
, 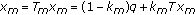 also converges to
also converges to 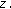 Since
Since  ,
, 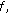 and
and 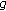 are continuous, we have
are continuous, we have 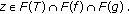 Thus
Thus 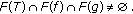
 is weakly compact, there is a subsequence
is weakly compact, there is a subsequence  of
of  converging weakly to some
converging weakly to some  . But,
. But,  and
and  being affine and continuous are weakly continuous, and the weak topology is Hausdorff, so we have
being affine and continuous are weakly continuous, and the weak topology is Hausdorff, so we have 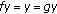 . The set
. The set 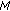 is bounded, so
is bounded, so  as
as  Now the demiclosedness of
Now the demiclosedness of 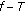 at
at  guarantees that
guarantees that 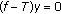 and hence
and hence 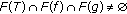 .
.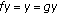 and
and  as
as 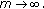 If
If 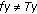 , then by the Opial's condition of
, then by the Opial's condition of 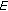 and
and 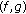 -nonexpansiveness of
-nonexpansiveness of 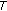 we get,
we get, 
 for each
for each  .
. is a Banach operator but
is a Banach operator but  and
and  are not
are not  -commuting maps and hence not a subcompatible pair.
-commuting maps and hence not a subcompatible pair.