- Research Article
- Open access
- Published:
Best Proximity Point Theorems for p-Cyclic Meir-Keeler Contractions
Fixed Point Theory and Applications volume 2009, Article number: 197308 (2009)
Abstract
We consider a contraction map  of the Meir-Keeler type on the union of p subsets
of the Meir-Keeler type on the union of p subsets  ,
,  , of a metric space (
, of a metric space ( ) to itself. We give sufficient conditions for the existence and convergence of a best proximity point for such a map.
) to itself. We give sufficient conditions for the existence and convergence of a best proximity point for such a map.
1. Introduction
Meir and Keeler in [1] considered an extension of the classical Banach contraction theorem on a complete metric space. Kirk et al. in [2] extended the Banach contraction theorem for a class of mappings satisfying cyclical contractive conditions. Eldred and Veeramani in [3] introduced the following definition. Let  and
and  be nonempty subsets of a metric space
be nonempty subsets of a metric space  . A map
. A map  , is a cyclic contraction map if it satisfies
, is a cyclic contraction map if it satisfies
(1) and
and  and
and
-
(2)
for some
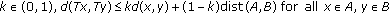 .
.
In this case, a point  such that
such that  , called a best proximity point, has been considered. This notion is more general in the sense that if the sets intersect, then every best proximity point is a fixed point. In [3], sufficient conditions for the existence and convergence of a unique best proximity point for a cyclic contraction on a uniformly convex Banach space have been given. Further, in [4], this result is extended by Di Bari et al., where the contraction condition of the map is of the Meir-Keeler-type. That is, in addition to the cyclic condition, if the map satisfies the condition that for a given
, called a best proximity point, has been considered. This notion is more general in the sense that if the sets intersect, then every best proximity point is a fixed point. In [3], sufficient conditions for the existence and convergence of a unique best proximity point for a cyclic contraction on a uniformly convex Banach space have been given. Further, in [4], this result is extended by Di Bari et al., where the contraction condition of the map is of the Meir-Keeler-type. That is, in addition to the cyclic condition, if the map satisfies the condition that for a given  there exists a
there exists a  such that
such that  implies that
implies that  . Then, such a map is called a cyclic Meir-Keeler map. In [4], sufficient conditions are given to obtain a unique best proximity point for such maps. One may refer to [5, 6] for similar types of notion of best proximity points. A question that naturally arises is whether the main results in [4] can be extended to p subsets,
. Then, such a map is called a cyclic Meir-Keeler map. In [4], sufficient conditions are given to obtain a unique best proximity point for such maps. One may refer to [5, 6] for similar types of notion of best proximity points. A question that naturally arises is whether the main results in [4] can be extended to p subsets,  ? From a geometrical point of view, for the cyclic Meir-Keeler contraction defined on the union of two sets, there is no question concerning the position of the sets. But in the case of more than two sets, the map is defined on the union of p sets,
? From a geometrical point of view, for the cyclic Meir-Keeler contraction defined on the union of two sets, there is no question concerning the position of the sets. But in the case of more than two sets, the map is defined on the union of p sets,  (Definition 3.5), so that the image of
(Definition 3.5), so that the image of  is contained in
is contained in  and the image of
and the image of  is contained in
is contained in  but not in
but not in  (
( and
and  ). Hence, it is interesting to extend the notion of the cyclic Meir-Keeler contraction to p sets,
). Hence, it is interesting to extend the notion of the cyclic Meir-Keeler contraction to p sets,  and we call this map a p-cyclic Meir-Keeler contraction. In this paper, we give sufficient conditions for the existence and convergence of a best proximity point for such a map (Theorem 3.13). Here, we observe that the distances between the adjacent sets are equal under this map, and this fact plays an important role in obtaining a best proximity point. Also, the obtained best proximity point is a periodic point of
and we call this map a p-cyclic Meir-Keeler contraction. In this paper, we give sufficient conditions for the existence and convergence of a best proximity point for such a map (Theorem 3.13). Here, we observe that the distances between the adjacent sets are equal under this map, and this fact plays an important role in obtaining a best proximity point. Also, the obtained best proximity point is a periodic point of  with period p. Moreover, if
with period p. Moreover, if  is a best proximity point in
is a best proximity point in  , then
, then  is a best proximity point in
is a best proximity point in  for
for 
2. Preliminaries
In this section, we give some basic definitions and concepts related to the main results. We begin with a definition due to Lim [7].
Definition 2.1.
A function  is called an L-function if
is called an L-function if  ,
,  and for every
and for every  there exists
there exists  such that
such that  for all
for all  .
.
Let  be a nonempty set, and let
be a nonempty set, and let  . Then, the following are equivalent.
. Then, the following are equivalent.
(1)For each  , there exists
, there exists  such that
such that 
(2)There exists an L-function  (nondecreasing, continuous) such that
(nondecreasing, continuous) such that  and
and  .
.
Lemma 2.3 (see [8]).
Let  be an L-function. Let
be an L-function. Let  be a nonincreasing sequence of nonnegative real numbers. Suppose
be a nonincreasing sequence of nonnegative real numbers. Suppose  for all
for all  with
with  , then,
, then,  .
.
It is well known that if  is a convex subset of a strictly convex normed linear space
is a convex subset of a strictly convex normed linear space  and
and  , then a best approximation of x from
, then a best approximation of x from  , if it exists, is unique.
, if it exists, is unique.
We use the following lemmas proved in [3].
Lemma 2.4.
Let  be a nonempty closed and convex subset and
be a nonempty closed and convex subset and  be a nonempty closed subset of a uniformly convex Banach space. Let
be a nonempty closed subset of a uniformly convex Banach space. Let  be sequences in
be sequences in  and let
and let  be a sequence in
be a sequence in  satisfying
satisfying
(1) ,
,
(2)for every  there exists
there exists  such that for all
such that for all  .
.
Then, for every  , there exists
, there exists  , such that for all
, such that for all  .
.
Lemma 2.5.
Let  be a nonempty closed and convex subsets and let
be a nonempty closed and convex subsets and let  be a nonempty closed subset of a uniformly convex Banach space. Let
be a nonempty closed subset of a uniformly convex Banach space. Let  be sequences in
be sequences in  and let
and let  be a sequence in
be a sequence in  satisfying
satisfying
(1) ,
,
(2) .
.
Then,  converges to zero.
converges to zero.
3. Main Results
Definition 3.1.
Let  be nonempty subsets of a metric space. Then,
be nonempty subsets of a metric space. Then,  is called a p-cyclic mapping if
is called a p-cyclic mapping if

A point  is said to be a best proximity point if
is said to be a best proximity point if  .
.
Definition 3.2.
Let  be nonempty subsets of a metric space
be nonempty subsets of a metric space  and
and  be a p-cyclic mapping.
be a p-cyclic mapping.  is called a p-cyclic nonexpansive mapping if
is called a p-cyclic nonexpansive mapping if

It is an interesting fact to note that the distances between the adjacent sets are equal under the p-cyclic nonexpansive mapping.
Lemma 3.3.
Let  be as in Definition 3.2. Then,
be as in Definition 3.2. Then,  for all i,
for all i,  .
.
Proof.
For  ,
,  ,
,  ,
,  implies
implies  . That is,
. That is,  .
.
Remark 3.4.
If  is a best proximity point, then since
is a best proximity point, then since  and since the distances between the adjacent sets are equal,
and since the distances between the adjacent sets are equal,  is a best proximity point of T in
is a best proximity point of T in  for
for  .
.
Definition 3.5.
Let  be nonempty subsets of a metric space
be nonempty subsets of a metric space  . Let
. Let  be a p-cyclic mapping.
be a p-cyclic mapping.  is called a p-cyclic Meir-Keeler contraction if for every
is called a p-cyclic Meir-Keeler contraction if for every  there exists
there exists  such that
such that

for all  for
for  .
.
Remark 3.6.
From Lemma 2.2, we see that  is a p-cyclic Meir-Keeler contraction if and only if there exists an L-function
is a p-cyclic Meir-Keeler contraction if and only if there exists an L-function  (nondecreasing and continuous) such that for all
(nondecreasing and continuous) such that for all  ,
,  ,
,  ,
, 
 .
.
Remark 3.7.
From Remark 3.6, if  is a p-cyclic Meir-Keeler contraction, then for
is a p-cyclic Meir-Keeler contraction, then for  ,
,  ,
,  , the following hold:
, the following hold:
(1)
(2)
Hence, every p-cyclic Meir-Keeler contraction is a p-cyclic nonexpansive map.
Lemma 3.8.
Let  be as in Definition 3.5, where each
be as in Definition 3.5, where each  is closed. Then, for every
is closed. Then, for every  for
for 
(1)
(2)
Proof.
To prove (1), Lemma 2.3 is used. Let  . If
. If  for some n, then
for some n, then  for all
for all  . Since
. Since  , we find that
, we find that  and this proves (1). Hence, assume
and this proves (1). Hence, assume  for all n. By Remark 3.7,
for all n. By Remark 3.7,  , and by Remark 3.6, there exists an L-function
, and by Remark 3.6, there exists an L-function  such that
such that

Hence,  . Therefore,
. Therefore,  .
.
Similarly, (2) can easily be proved.
Remark 3.9.
From Lemma 3.8, if  is a uniformly convex Banach space and if each
is a uniformly convex Banach space and if each  is convex, then for
is convex, then for  ,
, 
 . Then, by Lemma 2.5,
. Then, by Lemma 2.5,  . Similarly,
. Similarly,  .
.
Theorem 3.10.
Let  be as in Definition 3.5. If for some i and for some
be as in Definition 3.5. If for some i and for some  , the sequence
, the sequence  in
in  contains a convergent subsequence
contains a convergent subsequence  converging to
converging to  , then
, then  is a best proximity point in
is a best proximity point in  .
.
Proof.

Therefore,  .
.
Let  be a metric space. Let
be a metric space. Let  be nonempty subsets of
be nonempty subsets of  and let
and let  be a p-cyclic map which satisfies the following condition. For given
be a p-cyclic map which satisfies the following condition. For given  there exists a
there exists a  such that
such that

for all  .
.
It follows from Lemma 2.2 that a p-cyclic map  satisfies the condition (3.6), if and only if there exists an L-function
satisfies the condition (3.6), if and only if there exists an L-function  (nondecreasing and continuous) such that for all
(nondecreasing and continuous) such that for all  ,
,  and for all i,
and for all i,  ,
,  ,
,  and
and  satisfies the p-cyclic nonexpansive property.
satisfies the p-cyclic nonexpansive property.
We use the following result due to Meir and Keeler [1] in the proof of Theorem 3.12.
Theorem 3.11.
Let  be a complete metric space, and let
be a complete metric space, and let  be such that for given
be such that for given  there exists a
there exists a  such that for all
such that for all  ,
,

Then,  has a unique fixed point
has a unique fixed point  . Moreover, for any
. Moreover, for any  , the sequence
, the sequence  converges to
converges to  .
.
Theorem 3.12.
Let  be a complete metric space. Let
be a complete metric space. Let  be nonempty closed subsets of
be nonempty closed subsets of  . Let
. Let  be a p-cyclic map satisfying (3.6). Then,
be a p-cyclic map satisfying (3.6). Then,  is nonempty and for any
is nonempty and for any  ,
,  , the sequence
, the sequence  converges to a unique fixed point in
converges to a unique fixed point in  .
.
Proof.
Let  . Let
. Let  . If
. If  for some n, then by the p-cyclic nonexpansive property of
for some n, then by the p-cyclic nonexpansive property of  ,
,  . Therefore, assume
. Therefore, assume  for all n. We note that the sequence
for all n. We note that the sequence  is nonincreasing, and there exists an L-function
is nonincreasing, and there exists an L-function  such that
such that  and by Lemma 2.3,
and by Lemma 2.3,  . Now,
. Now,

Also, consider

Fix  . By the definition of L-function, there exists
. By the definition of L-function, there exists  such that
such that  .
.
Choose an  satisfying
satisfying



Let us show that

Let us do this by the method of induction. From (3.12), it is clear that (3.13) holds for  . Fix
. Fix  . Assume that (3.7) is true for
. Assume that (3.7) is true for  . Now,
. Now,

By induction, (3.13) holds for all  . Now, for all
. Now, for all  ,
,

Therefore,  is a Cauchy sequence and converges to a point
is a Cauchy sequence and converges to a point  . Consider
. Consider

Therefore,  . Since
. Since  for all j,
for all j,  , and since
, and since  ,
,  for all i,
for all i,  . Therefore,
. Therefore,  is a fixed point. Let
is a fixed point. Let  . Restricting
. Restricting  , we see that
, we see that  is a Meir-Keeler contraction on the complete metric space
is a Meir-Keeler contraction on the complete metric space  . Hence, by Theorem 3.11, z is the unique fixed point in
. Hence, by Theorem 3.11, z is the unique fixed point in  .
.
Now, we prove our main result.
Theorem 3.13.
Let  be nonempty, closed, and convex subsets of a uniformly convex Banach space. Let
be nonempty, closed, and convex subsets of a uniformly convex Banach space. Let  be a p-cyclic Meir-Keeler contraction. Then, for each i,
be a p-cyclic Meir-Keeler contraction. Then, for each i,  , there exists a unique
, there exists a unique  such that for any
such that for any  , the sequence
, the sequence  converges to
converges to  , which is a best proximity point in
, which is a best proximity point in  . Moreover,
. Moreover,  is a periodic point of period p, and
is a periodic point of period p, and  is a best proximity point in
is a best proximity point in  for
for  .
.
Proof.
If  for some i, then
for some i, then  for all i, and hence,
for all i, and hence,  is nonempty. In this case,
is nonempty. In this case,  has a unique fixed point in the intersection. Therefore, assume
has a unique fixed point in the intersection. Therefore, assume  for all i. Let
for all i. Let  . There exists an L-function
. There exists an L-function  as given in Remark 3.6. Fix
as given in Remark 3.6. Fix  . Choose
. Choose  satisfying
satisfying  . By Remark 3.9,
. By Remark 3.9,  . Hence, there exists
. Hence, there exists  such that
such that

Let us prove that

Fix  . It is clear that (3.18) is true for
. It is clear that (3.18) is true for  . Assume that (3.18) is true for
. Assume that (3.18) is true for  . Now,
. Now,

Hence, (3.18) holds for  . Therefore, by induction, (3.18) is true for all
. Therefore, by induction, (3.18) is true for all  . Note that
. Note that  . Now, by Lemma 2.4, for every
. Now, by Lemma 2.4, for every  , there exists
, there exists  such that for every
such that for every  ,
,  Hence,
Hence,  is a Cauchy sequence and converges to
is a Cauchy sequence and converges to  . By Theorem 3.10, z is a best proximity point in
. By Theorem 3.10, z is a best proximity point in  . That is,
. That is,  . Let
. Let  such that
such that  and such that
and such that  . Then, by Theorem 3.10,
. Then, by Theorem 3.10,  is a best proximity point. That is,
is a best proximity point. That is,  . Let us show that
. Let us show that  . To do this,
. To do this,

Since  is a convex set and
is a convex set and  is a uniformly convex Banach space,
is a uniformly convex Banach space,  . Similarly, we can prove that
. Similarly, we can prove that  . Now,
. Now,

Since  is convex,
is convex,  . Now,
. Now,  . If
. If  then there is nothing to prove. Therefore, let
then there is nothing to prove. Therefore, let  . This implies that
. This implies that

Thus,  a contradiction. Hence,
a contradiction. Hence,  . Since
. Since  and
and  is convex,
is convex,  .
.
References
Meir A, Keeler E: A theorem on contraction mappings. Journal of Mathematical Analysis and Applications 1969,28(2):326–329. 10.1016/0022-247X(69)90031-6
Kirk WA, Srinivasan PS, Veeramani P: Fixed points for mappings satisfying cyclical contractive conditions. Fixed Point Theory 2003,4(1):79–89.
Eldred AA, Veeramani P: Existence and convergence of best proximity points. Journal of Mathematical Analysis and Applications 2006,323(2):1001–1006. 10.1016/j.jmaa.2005.10.081
Di Bari C, Suzuki T, Vetro C: Best proximity points for cyclic Meir-Keeler contractions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3790–3794. 10.1016/j.na.2007.10.014
Amini-Harandi A, Farajzadeh AP, O'Regan D, Agarwal RP: Coincidence point, best approximation and best proximity theorems for condensing set-valued maps in hyperconvex metric spaces. Fixed Point Theory and Applications, accepted
Amini-Harandi A, Farajzadeh AP, O'Regan D, Agarwal RP: Best proximity pairs for upper semicontinuous set-valued maps in hyperconvex metric spaces. Fixed Point Theory and Applications 2008, Article ID 648985, 2008:-5.
Lim T-C: On characterizations of Meir-Keeler contractive maps. Nonlinear Analysis: Theory, Methods & Applications 2001,46(1):113–120. 10.1016/S0362-546X(99)00448-4
Suzuki T: Some notes on Meir-Keeler contractions and -functions. Bulletin of the Kyushu Institute of Technology 2006, (53):1–13.
Acknowledgment
The authors would like to thank referee(s) for many useful comments and suggestions for the improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Karpagam, S., Agrawal, S. Best Proximity Point Theorems for p-Cyclic Meir-Keeler Contractions. Fixed Point Theory Appl 2009, 197308 (2009). https://doi.org/10.1155/2009/197308
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/197308
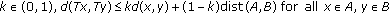 .
.