Skip to main content
Fixed Point Theory and Algorithms for Sciences and Engineering
Download PDF

Stability of the Cauchy-Jensen Functional Equation in 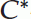-Algebras: A Fixed Point Approach

Fixed Point Theory and Applications volume 2008, Article number: 872190 (2006) Cite this article

Abstract

we prove the Hyers-Ulam-Rassias stability of -algebra homomorphisms and of generalized derivations on -algebras for the following Cauchy-Jensen functional equation , which was introduced and investigated by Baak (2006). The concept of Hyers-Ulam-Rassias stability originated from the stability theorem of Th. M. Rassias that appeared in (1978).

Publisher note

To access the full article, please see PDF.

Author information

Authors and Affiliations

  1. Department of Mathematics, Hanyang University, Seoul, 133-791, South Korea

    Choonkil Park

  2. Department of Mathematics Education, Pusan National University, Pusan, 609-735, South Korea

    Jong Su An

Authors
  1. Choonkil Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jong Su An
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jong Su An.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Park, C., An, J.S. Stability of the Cauchy-Jensen Functional Equation in 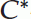-Algebras: A Fixed Point Approach. Fixed Point Theory Appl 2008, 872190 (2006). https://doi.org/10.1155/2008/872190

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2008/872190

Keywords