- Research Article
- Open access
- Published:
Strong Convergence Theorems for Nonexpansive Semigroups without Bochner Integrals
Fixed Point Theory and Applications volume 2008, Article number: 745010 (2008)
Abstract
We prove a convergence theorem by the new iterative method introduced by Takahashi et al. (2007). Our result does not use Bochner integrals so it is different from that by Takahashi et al. We also correct the strong convergence theorem recently proved by He and Chen (2007).
1. Introduction
Let  be a real Hilbert space with the inner product
be a real Hilbert space with the inner product  and the norm
and the norm  . Let
. Let  be a family of mappings from a subset
be a family of mappings from a subset  of
of  into itself. We call it a nonexpansive semigroup on
into itself. We call it a nonexpansive semigroup on  if the following conditions are satisfied:
if the following conditions are satisfied:
-
(1)
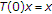 for all
for all 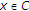 ;
; -
(2)
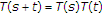 for all
for all 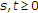 ;
; -
(3)
for each
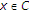 the mapping
the mapping 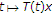 is continuous;
is continuous; -
(4)
 for all
for all 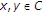 and
and 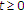 .
.
Motivated by Suzuki's result [1] and Nakajo-Takahashi's results [2], He and Chen [3] recently proved a strong convergence theorem for nonexpansive semigroups in Hilbert spaces by hybrid method in the mathematical programming. However, their proof of the main result ([3, Theorem 2.3]) is very questionable. Indeed, the existence of the subsequence  such that (2.16) of [3] are satisfied, that is,
such that (2.16) of [3] are satisfied, that is,

needs to be proved precisely. So, the aim of this short paper is to correct He-Chen's result and also to give a new result by using the method recently introduced by Takahashi et al.
We need the following lemma proved by Suzuki [4, Lemma 1].
Lemma 1.1.
Let  be a real sequence and let
be a real sequence and let  be a real number such that
be a real number such that  . Suppose that either of the following holds:
. Suppose that either of the following holds:
-
(i)
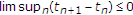 , or
, or -
(ii)
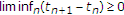 .
.
Then  is a cluster point of
is a cluster point of  . Moreover, for
. Moreover, for  ,
,  , there exists
, there exists  such that
such that  for every integer
for every integer  with
with  .
.
2. Results
2.1. The Shrinking Projection Method
The following method is introduced by Takahashi et al. in [5]. We use this method to approximate a common fixed point of a nonexpansive semigroup without Bochner integrals as was the case in [5, Theorem 4.4].
Theorem 2.1.
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  . Let
. Let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  with a nonempty common fixed point
with a nonempty common fixed point  , that is,
, that is,  . Suppose that
. Suppose that  is a sequence iteratively generated by the following scheme:
is a sequence iteratively generated by the following scheme:

where  ,
,  ,
,  , and
, and  . Then
. Then 
Proof.
It is well known that  is closed and convex. We first show that the iterative scheme is well defined. To see that each
is closed and convex. We first show that the iterative scheme is well defined. To see that each  is nonempty, it suffices to show that
is nonempty, it suffices to show that  . The proof is by induction. Clearly,
. The proof is by induction. Clearly,  . Suppose that
. Suppose that  . Then, for
. Then, for  ,
,

That is,  as required.
as required.
Notice that

is convex since

This implies that each subset  is convex. It is also clear that
is convex. It is also clear that  is closed. Hence the first claim is proved.
is closed. Hence the first claim is proved.
Next, we prove that  is bounded. As
is bounded. As  ,
,

In particular, for  for all
for all  , the sequence
, the sequence  is bounded and hence so is
is bounded and hence so is  .
.
Next, we show that  is a Cauchy sequence. As
is a Cauchy sequence. As  and
and  ,
,

Moreover, since the sequence  is bounded,
is bounded,

Note that

In particular, since  for all
for all  ,
,

It then follows from the existence of  that
that  is a Cauchy sequence. In fact, for
is a Cauchy sequence. In fact, for  , there exists a natural number
, there exists a natural number  such that, for all
such that, for all  ,
,

where  . In particular, if
. In particular, if  and
and  , then
, then

Moreover,

We now assume that  for some
for some  . Now since
. Now since  for all
for all  and
and  ,
,

The last convergence follows from (2.12). We choose a sequence  of positive real number such that
of positive real number such that

We now show that how such a special subsequence can be constructed. First we fix  such that
such that

From (2.13), there exists  such that
such that  for all
for all  . By Lemma 1.1,
. By Lemma 1.1,  is a cluster point of
is a cluster point of  . In particular, there exists
. In particular, there exists  such that
such that  . Next, we choose
. Next, we choose  such that
such that  for all
for all  . Again, by Lemma 1.1,
. Again, by Lemma 1.1,  is a cluster point of
is a cluster point of  and this implies that there exists
and this implies that there exists  such that
such that  . Continuing in this way, we obtain a subsequence
. Continuing in this way, we obtain a subsequence  of
of  satisfying
satisfying

Consequently, (2.14) is satisfied.
We next show that  . To see this, we fix
. To see this, we fix  ,
,

As  and (2.14), we have
and (2.14), we have  and so
and so  .
.
Finally, we show that  . Since
. Since  and
and  ,
,

But  ; we have
; we have

Hence  as required. This completes the proof.
as required. This completes the proof.
2.2. The Hybrid Method
We consider the iterative scheme computing by the hybrid method (some authors call the CQ-method). The following result is proved by He and Chen [3]. However, the important part of the proof seems to be overlooked. Here we present the correction under some additional restriction on the parameter  .
.
Theorem 2.2.
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  . Let
. Let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  with a nonempty common fixed point
with a nonempty common fixed point  , that is,
, that is,  . Suppose that
. Suppose that  is a sequence iteratively generated by the following scheme:
is a sequence iteratively generated by the following scheme:

where  ,
,  ,
,  , and
, and  . Then
. Then  .
.
Proof.
For the sake of clarity, we give the whole sketch proof even though some parts of the proof are the same as [3]. To see that the scheme is well defined, it suffices to show that both  and
and  are closed and convex, and
are closed and convex, and  for all
for all  . It follows easily from the definition that
. It follows easily from the definition that  and
and  are just the intersection of
are just the intersection of  and the half-spaces, respectively,
and the half-spaces, respectively,

As in the proof of the preceding theorem, we have  for all
for all  . Clearly,
. Clearly,  . Suppose that
. Suppose that  for some
for some  , we have
, we have  . In particular,
. In particular,  , that is,
, that is,  . It follows from the induction that
. It follows from the induction that  for all
for all  . This proves the claim.
. This proves the claim.
We next show that  . To see this, we first prove that
. To see this, we first prove that

As  and
and  ,
,

For fixed  . It follows from
. It follows from  for all
for all  that
that

This implies that sequence  is bounded and
is bounded and

Notice that

This implies that

It then follows from  that
that  and hence
and hence

As in Theorem 2.1, we can choose a subsequence  of
of  such that
such that

Consequently, for any  ,
,

This implies that

In virtue of Opial's condition of  , we have
, we have  for all
for all  , that is,
, that is,  . Next, we observe that
. Next, we observe that

This implies that

Consequently,

Hence the whole sequence must converge to  , as required.
, as required.
References
Suzuki T: On strong convergence to common fixed points of nonexpansive semigroups in Hilbert spaces. Proceedings of the American Mathematical Society 2003, 131(7):2133-2136. 10.1090/S0002-9939-02-06844-2
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. Journal of Mathematical Analysis and Applications 2003, 279(2):372-379. 10.1016/S0022-247X(02)00458-4
He H, Chen R: Strong convergence theorems of the CQ method for nonexpansive semigroups. Fixed Point Theory and Applications 2007, 2007:-8.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005, 305(1):227-239. 10.1016/j.jmaa.2004.11.017
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 341(1):276-286.
Acknowledgments
The author would like to thank the referee(s) for his comments and suggestions on the manuscript. This work is supported by the Commission on Higher Education and the Thailand Research Fund (Grant MRG4980022).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saejung, S. Strong Convergence Theorems for Nonexpansive Semigroups without Bochner Integrals. Fixed Point Theory Appl 2008, 745010 (2008). https://doi.org/10.1155/2008/745010
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/745010
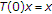 for all
for all 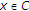 ;
;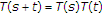 for all
for all 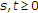 ;
;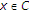 the mapping
the mapping 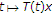 is continuous;
is continuous; for all
for all 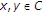 and
and 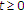 .
.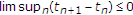 , or
, or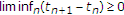 .
.