- Research Article
- Open access
- Published:
Composite Implicit General Iterative Process for a Nonexpansive Semigroup in Hilbert Space
Fixed Point Theory and Applications volume 2008, Article number: 484050 (2008)
Abstract
Let  be nonempty closed convex subset of real Hilbert space
be nonempty closed convex subset of real Hilbert space  . Consider
. Consider  a nonexpansive semigroup
a nonexpansive semigroup  with a common fixed point, a contraction
with a common fixed point, a contraction  with coefficient
with coefficient  , and a strongly positive linear bounded operator
, and a strongly positive linear bounded operator  with coefficient
with coefficient  . Let
. Let  . It is proved that the sequence
. It is proved that the sequence  generated iteratively by
generated iteratively by  converges strongly to a common fixed point
converges strongly to a common fixed point  which solves the variational inequality
which solves the variational inequality  for all
for all  .
.
1. Introduction and Preliminaries
Let  be a closed convex subset of a Hilbert space
be a closed convex subset of a Hilbert space  , recall that
, recall that  is nonexpansive if
is nonexpansive if  for all
for all  . Denote by
. Denote by  the set of fixed points of
the set of fixed points of  , that is,
, that is,  .
.
Recall that a family  of mappings from
of mappings from  into itself is called a nonexpansive semigroup on
into itself is called a nonexpansive semigroup on  if it satisfies the following conditions:
if it satisfies the following conditions:
-
(i)
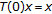 for all
for all 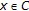 ;
; -
(ii)
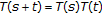 for all
for all  ;
; -
(iii)
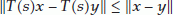 for all
for all  and
and 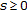 ;
; -
(iv)
for all
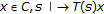 is continuous.
is continuous.
We denote by  the set of all common fixed points of
the set of all common fixed points of  , that is,
, that is,  . It is known that
. It is known that  is closed and convex.
is closed and convex.
Iterative methods for nonexpansive mappings have recently been applied to solve convex minimization problems (see, e.g., [1–5] and the references therein). A typical problem is to minimize a quadratic function over the set of the fixed points of a nonexpansive mapping on a real Hilbert space  :
:

where  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  on
on  , and
, and  is a given point in
is a given point in  . Assume that
. Assume that  is strongly positive, that is, there is a constant
is strongly positive, that is, there is a constant  with the property
with the property

It is well known that  is closed convex (cf. [6]). In[3] (see also [4]), it is proved that the sequence
is closed convex (cf. [6]). In[3] (see also [4]), it is proved that the sequence  defined by the iterative method below, with the initial guess
defined by the iterative method below, with the initial guess  chosen arbitrarily,
chosen arbitrarily,

converges strongly to the unique solution of the minimization problem (1.1) provided that the sequence  satisfies certain conditions.
satisfies certain conditions.
On the other hand, Moudafi [7] introduced the viscosity approximation method for nonexpansive mappings (see [8] for further developments in both Hilbert and Banach spaces). Let  be a contraction on
be a contraction on  . Starting with an arbitrary initial
. Starting with an arbitrary initial  , define a sequence
, define a sequence  recursively by
recursively by

where  is a sequence in (
is a sequence in ( ). It is proved [7, 8] that under certain appropriate conditions imposed on
). It is proved [7, 8] that under certain appropriate conditions imposed on  , the sequence
, the sequence  generated by (1.4) strongly converges to the unique solution
generated by (1.4) strongly converges to the unique solution  in
in  of the variational inequality
of the variational inequality

Recently, Marino and Xu [9] combined the iterative method (1.3) with the viscosity approximation method (1.4) considering the following general iteration process:

and proved that if the sequence  satisfies appropriate conditions, then the sequence
satisfies appropriate conditions, then the sequence  generated by (1.6) converges strongly to the unique solution of the variational inequality
generated by (1.6) converges strongly to the unique solution of the variational inequality

which is the optimality condition for the minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  , for
, for  ).
).
In this paper, motivated and inspired by the idea of Marino and Xu [9], we introduce the composite implicit general iteration process (1.9) as follows:

where  , and investigate the problem of approximating common fixed point of nonexpansive semigroup
, and investigate the problem of approximating common fixed point of nonexpansive semigroup  which solves some variational inequality. The results presented in this paper extend and improve the main results in Marino and Xu [9], and the methods of proof given in this paper are also quite different.
which solves some variational inequality. The results presented in this paper extend and improve the main results in Marino and Xu [9], and the methods of proof given in this paper are also quite different.
In what follows, we will make use of the following lemmas. Some of them are known; others are not hard to derive.
Lemma 1.1 (Marino and Xu [9]).
Assume that  is a strongly positive linear bounded operator on a Hilbert space
is a strongly positive linear bounded operator on a Hilbert space  with coefficient
with coefficient  and
and  . Then
. Then  .
.
Lemma (Shimizu and Takashi [10]).
Let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  and let
and let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  , then for any
, then for any  ,
,

Lemma 1.3.
Let  be a nonempty bounded closed convex subset of a Hilbert space
be a nonempty bounded closed convex subset of a Hilbert space  and let
and let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  . If
. If  is a sequence in
is a sequence in  satisfying the following properties:
satisfying the following properties:
-
(i)
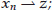
-
(ii)
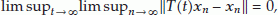
where 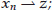 denote that
denote that  converges weakly to
converges weakly to  , then
, then  .
.
Proof.
This lemma is the continuous version of Lemma 2.3 of Tan and Xu [11]. This proof given in [11] is easily extended to the continuous case.
2. Main Results
Lemma 2.1.
Let  be a Hilbert space,
be a Hilbert space,  a closed convex subset of
a closed convex subset of  , let
, let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  ,
,  is a sequence, then
is a sequence, then  is monotone.
is monotone.
Proof.
In fact, for all  ,
,

Theorem 2.2.
Let  be nonempty closed convex subset of real Hilbert space
be nonempty closed convex subset of real Hilbert space  , suppose that
, suppose that  is a fixed contractive mapping with coefficient
is a fixed contractive mapping with coefficient  , and
, and  is a nonexpansive semigroup on
is a nonexpansive semigroup on  such that
such that  is nonempty, and
is nonempty, and  is a strongly positive linear bounded operator with coefficient
is a strongly positive linear bounded operator with coefficient  ,
,  ,
,  are real sequences such that
are real sequences such that

then for any  , there is a unique
, there is a unique  such that
such that

and the iteration process  converges strongly to the unique solution
converges strongly to the unique solution  of the variational inequality
of the variational inequality  for all
for all  .
.
Proof.
Our proof is divided into five steps.
Since  ,
,  as
as  , we may assume, with no loss of generality, that
, we may assume, with no loss of generality, that  ,
,  for all
for all  .
.
(i) is bounded.
is bounded.
Firstly, we will show that the mapping  defined by
defined by

is a contraction. Indeed, from Lemma 1.1, we have for any  that
that

Let  be the unique fixed point of
be the unique fixed point of  . Thus,
. Thus,

is well defined. Next, we will show that  is bounded.
is bounded.
Pick any  to obtain
to obtain


Also

Substituting (2.9) into (2.8), we obtain that

Thus  is bounded.
is bounded.
(ii) .
.
Denote that  , since
, since  is bounded,
is bounded,  and
and  ,
,  are also bounded, From (2.6) and
are also bounded, From (2.6) and  , we have
, we have

Let  , then
, then  is a nonempty bounded closed convex subset of
is a nonempty bounded closed convex subset of  and
and  -invariant. Since
-invariant. Since  and
and  is bounded, there exists
is bounded, there exists  such that
such that  , it follows from Lemma 1.2 that
, it follows from Lemma 1.2 that

From (2.11) and (2.12), we have

(iii)There exists a subsequence  of
of  such that
such that  and
and  is the unique solution of the following variational inequality:
is the unique solution of the following variational inequality:

Firstly since

From condition  and the boundedness of
and the boundedness of  , we obtain that
, we obtain that  . Again by boundedness of
. Again by boundedness of  , we know that there exists a subsequence
, we know that there exists a subsequence  of
of  such that
such that  . Then
. Then  . From Lemma 1.3 and step (ii), we have that
. From Lemma 1.3 and step (ii), we have that  .
.
Next we will prove that  solves the variational inequality (2.14). Since
solves the variational inequality (2.14). Since

we derive that

It follows that, for all  ,
,

Using Lemma 2.1, we have from (2.18) that

Now replacing  in (2.19) with
in (2.19) with  and letting
and letting  , we notice that
, we notice that

and from condition  and boundedness of
and boundedness of  , we have
, we have

For  , we obtain
, we obtain

From [9, Theorem 3.2], we know that the solution of the variational inequality (2.14) is unique. That is,  is a unique solution of (2.14).
is a unique solution of (2.14).
-
(iv)
 (2.23)
(2.23)
where  is obtained in step (iii).
is obtained in step (iii).
To see this, there exists a subsequence  of
of  such that
such that

we may also assume that  , then
, then  , note from step (ii) that
, note from step (ii) that  in virtue of Lemma 1.2. It follows from the variational inequality (2.14) that
in virtue of Lemma 1.2. It follows from the variational inequality (2.14) that

So (2.23) holds thank to (2.14).
(v) .
.
Finally, we will prove  . Since
. Since

Next, we calculate

Thus it follows from (2.26) that

Thus

Since  is bounded, we can take a constant
is bounded, we can take a constant  such that
such that

for all  . It then follows from (2.29) that
. It then follows from (2.29) that

Then

From condition  ,
,  and (2.23), we conclude that
and (2.23), we conclude that

So  . This completes the proof of the Theorem 2.2.
. This completes the proof of the Theorem 2.2.
It follows from the above proof that Theorem 2.2 is valid for nonexpansive mappings. Thus, we have that Corollaries 2.3 and 2.4 are two special cases of Theorem 2.2.
Corollary 2.3.
Let  be a nonexpansive mapping from nonempty closed convex subset
be a nonexpansive mapping from nonempty closed convex subset  of a Hilbert space
of a Hilbert space  to
to  ,
,  is generated by the following algorithm:
is generated by the following algorithm:

where  are real sequences such that
are real sequences such that

then for any  , the sequence
, the sequence  above converges strongly to the unique solution
above converges strongly to the unique solution  of the variational inequality
of the variational inequality  for all
for all  .
.
Corollary 2.4.
Let  be a nonexpansive mapping from nonempty closed convex subset
be a nonexpansive mapping from nonempty closed convex subset  of a Hilbert space
of a Hilbert space  to
to  ,
,  is generated by the following algorithm:
is generated by the following algorithm:

where  is a sequence in (
is a sequence in ( ) satisfying the following condition:
) satisfying the following condition:  , then the sequence
, then the sequence  converges strongly to the unique solution
converges strongly to the unique solution  of the variational inequality
of the variational inequality  for all
for all  .
.
References
Deutsch F, Yamada I: Minimizing certain convex functions over the intersection of the fixed point sets of nonexpansive mappings. Numerical Functional Analysis and Optimization 1998, 19(1-2):33-56.
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002, 66(1):240-256. 10.1112/S0024610702003332
Xu H-K: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003, 116(3):659-678. 10.1023/A:1023073621589
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications (Haifa, 2000), Studies in Computational Mathematics. Volume 8. Edited by: Butnariu D, Censor Y, Reich S. North-Holland, Amsterdam, The Netherlands; 2001:473-504.
Yamada I, Ogura N, Yamashita Y, Sakaniwa K: Quadratic optimization of fixed points of nonexpansive mappings in Hilbert space. Numerical Functional Analysis and Optimization 1998, 19(1-2):165-190. 10.1080/01630569808816822
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000, 241(1):46-55. 10.1006/jmaa.1999.6615
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004, 298(1):279-291. 10.1016/j.jmaa.2004.04.059
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006, 318(1):43-52. 10.1016/j.jmaa.2005.05.028
Shimizu T, Takahashi W: Strong convergence to common fixed points of families of nonexpansive mappings. Journal of Mathematical Analysis and Applications 1997, 211(1):71-83. 10.1006/jmaa.1997.5398
Tan K-K, Xu H-K: The nonlinear ergodic theorem for asymptotically nonexpansive mappings in Banach spaces. Proceedings of the American Mathematical Society 1992, 114(2):399-404. 10.1090/S0002-9939-1992-1068133-2
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, L., Li, S. & Su, Y. Composite Implicit General Iterative Process for a Nonexpansive Semigroup in Hilbert Space. Fixed Point Theory Appl 2008, 484050 (2008). https://doi.org/10.1155/2008/484050
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/484050
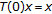 for all
for all 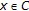 ;
;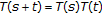 for all
for all  ;
;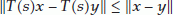 for all
for all  and
and 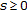 ;
;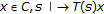 is continuous.
is continuous.