- Research Article
- Open access
- Published:
Convergence Theorems for Common Fixed Points of Nonself Asymptotically Quasi-Non-Expansive Mappings
Fixed Point Theory and Applications volume 2008, Article number: 428241 (2008)
Abstract
We introduce a new three-step iterative scheme with errors. Several convergence theorems of this scheme are established for common fixed points of nonself asymptotically quasi-non-expansive mappings in real uniformly convex Banach spaces. Our theorems improve and generalize recent known results in the literature.
1. Introduction
Let  be a nonempty closed convex subset of real normed linear space
be a nonempty closed convex subset of real normed linear space  . Recall that a mapping
. Recall that a mapping  is called asymptotically nonexpansive if there exists a sequence
is called asymptotically nonexpansive if there exists a sequence  , with
, with  such that
such that  for all
for all  and
and  . Moreover, it is uniformly
. Moreover, it is uniformly  -Lipschitzian if there exists a constant
-Lipschitzian if there exists a constant  such that
such that  for all
for all  and each
and each  . Denote and define by
. Denote and define by  the set of fixed points of
the set of fixed points of  . Suppose
. Suppose  . A mapping
. A mapping  is called asymptotically quasi-non-expansive if there exists a sequence
is called asymptotically quasi-non-expansive if there exists a sequence  , with
, with  such that
such that  for all
for all  ,
,  , and
, and  .
.
It is clear from the above definitions that an asymptotically nonexpansive mapping must be uniformly  -Lipschitzian as well as asymptotically quasi-non-expansive, but the converse does not hold. Iterative technique for asymptotically nonexpansive self-mapping in Hilbert spaces and Banach spaces including Mann-type and Ishikawa-type iteration processes has been studied extensively by many authors; see, for example, [1–6].
-Lipschitzian as well as asymptotically quasi-non-expansive, but the converse does not hold. Iterative technique for asymptotically nonexpansive self-mapping in Hilbert spaces and Banach spaces including Mann-type and Ishikawa-type iteration processes has been studied extensively by many authors; see, for example, [1–6].
Recently, Chidume etal. [7] have introduced the concept of nonself asymptotically nonexpansive mappings, which is the generalization of asymptotically nonexpansive mappings. Similarly, the concept of nonself asymptotically quasi-non-expansive mappings can also be defined as the generalization of asymptotically quasi-non-expansive mappings and nonself asymptotically nonexpansive mappings. These mappings are defined as follows.
Definition 1.1.
Let  be a nonempty closed convex subset of real normed linear space
be a nonempty closed convex subset of real normed linear space  , let
, let  be the nonexpansive retraction of
be the nonexpansive retraction of  onto
onto  , and let
, and let  be a nonself mapping.
be a nonself mapping.
-
(i)
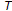 is said to be a nonself asymptotically nonexpansive mapping if there exists a sequence
is said to be a nonself asymptotically nonexpansive mapping if there exists a sequence 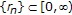 , with
, with 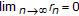 such that
such that 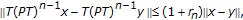 (1.1)
(1.1)
for all  and
and  .
.
-
(ii)
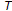 is said to be a nonself uniformly
is said to be a nonself uniformly 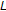 -Lipschitzian mapping if there exists a constant
-Lipschitzian mapping if there exists a constant 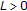 such that
such that  (1.2)
(1.2)
for all  and
and  .
.
-
(iii)
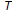 is said to be a nonself asymptotically quasi-non-expansive mapping if
is said to be a nonself asymptotically quasi-non-expansive mapping if  and there exists a sequence
and there exists a sequence 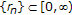 , with
, with  such that
such that  (1.3)
(1.3)
for all  ,
,  , and
, and  .
.
By studying the following iteration process (Mann-type iteration):

where  , Chidume etal. [7] obtained many convergence theorems for the fixed points of nonself asymptotically nonexpansive mapping
, Chidume etal. [7] obtained many convergence theorems for the fixed points of nonself asymptotically nonexpansive mapping  . Later on, Wang [8] generalized the iteration process (1.4) as follows (Ishikawa-type iteration):
. Later on, Wang [8] generalized the iteration process (1.4) as follows (Ishikawa-type iteration):

where  are nonself asymptotically nonexpansive mappings and
are nonself asymptotically nonexpansive mappings and  . Also, he got several convergence theorems of the iterative scheme (1.5) under proper conditions.
. Also, he got several convergence theorems of the iterative scheme (1.5) under proper conditions.
In 2000, Noor [9] first introduced a three-step iterative sequence and studied the approximate solutions of variational inclusion in Hilbert spaces by using the techniques of updating the solution and the auxiliary principle. Glowinski and Tallec [10] showed that the three-step iterative schemes perform better than the Mann-type and Ishikawa-type iterative schemes. On the other hand, Xu and Noor [11] introduced and studied a three-step scheme to approximate fixed points of asymptotically nonexpansive mappings in Banach spaces. Cho etal. [12] and Plubtieng etal. [13] extended the work of Xu and Noor to the three-step iterative scheme with errors, and gave weak and strong convergence theorems for asymptotically nonexpansive mappings in Banach spaces.
Inspired and motivated by these facts, a new class of three-step iterative schemes with errors, for three nonself asymptotically quasi-non-expansive mappings, is introduced and studied in this paper. This scheme can be viewed as an extension for (1.4), (1.5), and others. This scheme is defined as follows.
Let  be a nonempty convex subset of real normed linear space
be a nonempty convex subset of real normed linear space  , let
, let  be the nonexpansive retraction of
be the nonexpansive retraction of  onto
onto  , and let
, and let  be three nonself asymptotically quasi-non-expansive mappings. Compute the sequences
be three nonself asymptotically quasi-non-expansive mappings. Compute the sequences  ,
,  , and
, and  by
by

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  are real sequences in
are real sequences in  with
with  , and
, and  ,
,  , and
, and  are bounded sequences in
are bounded sequences in  .
.
Remark 1.2.
-
(i)
If
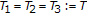 ,
, 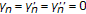 , and
, and  , then scheme (1.6) reduces to the Mann-type iteration (1.4).
, then scheme (1.6) reduces to the Mann-type iteration (1.4). -
(ii)
If
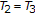 ,
,  , and
, and 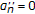 , then scheme (1.6) reduces to the Ishikawa-type iteration (1.5).
, then scheme (1.6) reduces to the Ishikawa-type iteration (1.5). -
(iii)
If
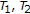 , and
, and 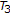 are three self-asymptotically nonexpansive mappings, then scheme (1.6) reduces to the three-step iteration with errors defined by [12, 13], and others.
are three self-asymptotically nonexpansive mappings, then scheme (1.6) reduces to the three-step iteration with errors defined by [12, 13], and others.
The purpose of this paper is to study the iterative sequences (1.6) to converge to a common fixed point of three nonself asymptotically quasi-non-expansive mappings in real uniformly convex Banach spaces. Our results extend and improve the corresponding results in [5, 7, 8, 11–13], and many others.
2. Preliminaries and Lemmas
In this section, we first recall some well-known definitions.
A real Banach space  is said to be uniformly convex if the modulus of convexity of
is said to be uniformly convex if the modulus of convexity of  :
:

for all  (i.e.,
(i.e.,  is a function
is a function  ).
).
A subset  of
of  is said to be a retract if there exists continuous mapping
is said to be a retract if there exists continuous mapping  such that
such that  , for all
, for all  , and every closed convex subset of a uniformly convex Banach space is a retract. A mapping
, and every closed convex subset of a uniformly convex Banach space is a retract. A mapping  is said to be a retraction if
is said to be a retraction if  .
.
A mapping  with
with  is said to satisfy condition (A) (see [14]) if there exists a nondecreasing function
is said to satisfy condition (A) (see [14]) if there exists a nondecreasing function  with
with  , for all
, for all  , such that
, such that

for all  , where
, where  .
.
We modify this condition for three mappings  as follows. Three mappings
as follows. Three mappings  , where
, where  is a subset of
is a subset of  , are said to satisfy condition (B) if there exist a real number
, are said to satisfy condition (B) if there exist a real number  and a nondecreasing function
and a nondecreasing function  with
with  , for all
, for all  , such that
, such that

for all  , where
, where  . Note that condition (B) reduces to condition (A) when
. Note that condition (B) reduces to condition (A) when  and
and  .
.
A mapping  is said to be semicompact if, for any sequence
is said to be semicompact if, for any sequence  in
in  such that
such that  , there exists subsequence
, there exists subsequence  of
of  such that
such that  converges strongly to
converges strongly to  .
.
Next we state the following useful lemmas.
Lemma 2.1 (see [5]).
Let  ,
,  , and
, and  be sequences of nonnegative real numbers satisfying the inequality
be sequences of nonnegative real numbers satisfying the inequality

If  and
and  , then
, then  exists.
exists.
Lemma 2.2 (see [15]).
Let  be a real uniformly convex Banach space and
be a real uniformly convex Banach space and  , for all positive integer
, for all positive integer  . Suppose that
. Suppose that  and
and  are two sequences of
are two sequences of  such that
such that  ,
,  , and
, and  hold, for some
hold, for some  ; then
; then  .
.
3. Main Results
In this section, we will prove the strong convergence of the iteration scheme (1.6) to a common fixed point of nonself asymptotically quasi-non-expansive mappings  , and
, and  . We first prove the following lemmas.
. We first prove the following lemmas.
Lemma 3.1.
Let  be a nonempty closed convex subset of a real normed linear space
be a nonempty closed convex subset of a real normed linear space  . Let
. Let  be nonself asymptotically quasi-non-expansive mappings with sequences
be nonself asymptotically quasi-non-expansive mappings with sequences  such that
such that  , for all
, for all  . Suppose that
. Suppose that  is defined by (1.6) with
is defined by (1.6) with  ,
,  , and
, and  . If
. If  , then
, then  exists, for all
exists, for all  .
.
Proof..
Let  . Since
. Since  , and
, and  are bounded sequences in
are bounded sequences in  , therefore there exists
, therefore there exists  such that
such that

Let  and
and  Then
Then  and
and  . By (1.6), we have
. By (1.6), we have


and similarly, we also have

Substituting (3.4) into (3.3), we obtain

where  . Since
. Since  and
and  , then
, then  . Substituting (3.5) into (3.2), we have
. Substituting (3.5) into (3.2), we have

where  and
and  . Since
. Since  ,
,  , and
, and  , then
, then  and
and  . It follows from Lemma 2.1 that
. It follows from Lemma 2.1 that  exists. This completes the proof.
exists. This completes the proof.
Lemma 3.2.
Let  be a nonempty closed convex subset of a real uniformly convex Banach space
be a nonempty closed convex subset of a real uniformly convex Banach space  . Let
. Let  be uniformly
be uniformly  -Lipschitzian nonself asymptotically quasi-non-expansive mappings with sequences
-Lipschitzian nonself asymptotically quasi-non-expansive mappings with sequences  such that
such that  , for all
, for all  . Suppose that
. Suppose that  is defined by (1.6) with
is defined by (1.6) with  ,
,  , and
, and  , where
, where  , and
, and  are three sequences in
are three sequences in  , for some
, for some  . If
. If  , then
, then

Proof..
For any  , by Lemma 3.1, we see that
, by Lemma 3.1, we see that  exists. Assume
exists. Assume  , for some
, for some  . For all
. For all  , let
, let  and
and 
Then,  and
and  . From (3.5), we have
. From (3.5), we have

Taking  on both sides in (3.8), since
on both sides in (3.8), since  and
and  , we obtain
, we obtain

so that

Next consider

Since  , we have
, we have

In addition,

This implies that

Further, observe that

By Lemma 2.2, (3.12), (3.14), and (3.15), we have

Next we will prove that  . Since
. Since

and  , we obtain
, we obtain

Thus, it follows from (3.10) and (3.18) that

On the other hand, from (3.4), we have

By boundedness of the sequence  and by
and by  , we have
, we have

so that

Next consider

Thus, we have

This implies that

Note that

It follows from Lemma 2.2, (3.24), and (3.25) that

Similarly, by using the same argument as in the proof above, we obtain

Hence,

and this implies that

Since  is uniformly
is uniformly  -Lipschitzian mapping, then we have
-Lipschitzian mapping, then we have


It follows from (3.30), (3.31), and (3.32) that

Next consider


It follows from (3.30), (3.34), and (3.35) that

Finally, we consider

It follows from (3.29), (3.30), and (3.37) that

Therefore,

This completes the proof.
Now, we give our main theorems of this paper.
Theorem 3.3.
Let  be a nonempty closed convex subset of a real uniformly convex Banach space
be a nonempty closed convex subset of a real uniformly convex Banach space  . Let
. Let  be uniformly
be uniformly  -Lipschitzian and nonself asymptotically quasi-non-expansive mappings with sequences
-Lipschitzian and nonself asymptotically quasi-non-expansive mappings with sequences  such that
such that  , for all
, for all  satisfying condition (B). Suppose that
satisfying condition (B). Suppose that  is defined by (1.6) with
is defined by (1.6) with  ,
,  , and
, and  , where
, where  , and
, and  are three sequences in
are three sequences in  , for some
, for some  . If
. If  , then
, then  converges strongly to a common fixed point of
converges strongly to a common fixed point of  , and
, and  .
.
Proof..
It follows from Lemma 3.2 that  . Since
. Since  , and
, and  satisfy condition (B), we have
satisfy condition (B), we have  .
.
From Lemma 3.1 and the proof of Qihou [5], we can obtain that  is a Cauchy sequence in
is a Cauchy sequence in  . Assume that
. Assume that  . Since
. Since  , by the continuity of
, by the continuity of  , and
, and  , we have
, we have  , that is,
, that is,  is a common fixed point of
is a common fixed point of  , and
, and  . This completes the proof.
. This completes the proof.
Corollary 3.4.
Let  be a nonempty closed convex subset of a real uniformly convex Banach space
be a nonempty closed convex subset of a real uniformly convex Banach space  . Let
. Let  be nonself asymptotically nonexpansive mappings with sequences
be nonself asymptotically nonexpansive mappings with sequences  such that
such that  , for all
, for all  satisfying condition (B). Suppose that
satisfying condition (B). Suppose that  is defined by (1.6) with
is defined by (1.6) with  ,
,  , and
, and  , where
, where  , and
, and  are three sequences in
are three sequences in  for some
for some  . If
. If  , then
, then  converges strongly to a common fixed point of
converges strongly to a common fixed point of  , and
, and  .
.
Proof..
Since every nonself asymptotically nonexpansive mapping is uniformly  -Lipschitzian and nonself asymptotically quasi-non-expansive, the result can be deduced immediately from Theorem 3.3. This completes the proof.
-Lipschitzian and nonself asymptotically quasi-non-expansive, the result can be deduced immediately from Theorem 3.3. This completes the proof.
Theorem 3.5.
Let  be a nonempty closed convex subset of a real uniformly convex Banach space
be a nonempty closed convex subset of a real uniformly convex Banach space  . Let
. Let  be uniformly
be uniformly  -Lipschitzian and nonself asymptotically quasi-non-expansive mappings with sequences
-Lipschitzian and nonself asymptotically quasi-non-expansive mappings with sequences  such that
such that  for all
for all  . Suppose that
. Suppose that  is defined by (1.6) with
is defined by (1.6) with  ,
,  , and
, and  , where
, where  , and
, and  are three sequences in
are three sequences in  for some
for some  . If
. If  and one of
and one of  , and
, and  is demicompact, then
is demicompact, then  converges strongly to a common fixed point of
converges strongly to a common fixed point of  , and
, and  .
.
Proof..
Without loss of generality, we may assume that  is demicompact. Since
is demicompact. Since  , there exists a subsequence
, there exists a subsequence  such that
such that  . Hence, from (3.39), we have
. Hence, from (3.39), we have

This implies that  . By the arbitrariness of
. By the arbitrariness of  , from Lemma 3.1, and taking
, from Lemma 3.1, and taking  , similarly we can prove that
, similarly we can prove that

where  is some nonnegative number. From
is some nonnegative number. From  , we know that
, we know that  , that is,
, that is,  . This completes the proof.
. This completes the proof.
Corollary 3.6.
Let  be a nonempty closed convex subset of a real uniformly convex Banach space
be a nonempty closed convex subset of a real uniformly convex Banach space  . Let
. Let  be nonself asymptotically nonexpansive mappings with sequences
be nonself asymptotically nonexpansive mappings with sequences  such that
such that  for all
for all  . Suppose that
. Suppose that  is defined by (1.6) with
is defined by (1.6) with  ,
,  , and
, and  , where
, where  , and
, and  are three sequences in
are three sequences in  for some
for some  . If
. If  and one of
and one of  , and
, and  is demicompact, then
is demicompact, then  converges strongly to a common fixed point of
converges strongly to a common fixed point of  , and
, and  .
.
References
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4(3):506-510. 10.1090/S0002-9939-1953-0054846-3
Ishikawa S: Fixed points and iteration of a nonexpansive mapping in a Banach space. Proceedings of the American Mathematical Society 1967, 59(1):65-71.
Tan KK, Xu HK: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. Journal of Mathematical Analysis and Applications 1993, 178(2):301-308. 10.1006/jmaa.1993.1309
Schu J: Weak and strong convergence to fixed points of asymptotically nonexpansive mappings. Bulletin of the Australian Mathematical Society 1991, 43(1):153-159. 10.1017/S0004972700028884
Liu QH: Iterative sequences for asymptotically quasi-nonexpansive mappings with error member. Journal of Mathematical Analysis and Applications 2001, 259(1):18-24. 10.1006/jmaa.2000.7353
Shahzad N, Udomene A: Approximating common fixed points of two asymptotically quasi-nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2006, 2006:-10.
Chidume CE, Ofoedu EU, Zegeye H: Strong and weak convergence theorems for asymptotically nonexpansive mappings. Journal of Mathematical Analysis and Applications 2003, 280(2):364-374. 10.1016/S0022-247X(03)00061-1
Wang L: Strong and weak convergence theorems for common fixed point of nonself asymptotically nonexpansive mappings. Journal of Mathematical Analysis and Applications 2006, 323(1):550-557. 10.1016/j.jmaa.2005.10.062
Noor MA: New approximation schemes for general variational inequalities. Journal of Mathematical Analysis and Applications 2000, 251(1):217-229. 10.1006/jmaa.2000.7042
Glowinski R, Le Tallec P: Augmented Lagrangian and Operator Splitting Methods in Nonlinear Mechanics, SIAM Studies in Applied Mathematics. Volume 9. SIAM, Philadelphia, Pa, USA; 1989:x+295.
Xu B, Noor MA: Fixed-point iterations for asymptotically nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2002, 267(2):444-453. 10.1006/jmaa.2001.7649
Cho YJ, Zhou H, Guo G: Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings. Computers & Mathematics with Applications 2004, 47(4-5):707-717. 10.1016/S0898-1221(04)90058-2
Plubtieng S, Wangkeeree R, Punpaeng R: On the convergence of modified Noor iterations with errors for asymptotically nonexpansive mappings. Journal of Mathematical Analysis and Applications 2006, 322(2):1018-1029. 10.1016/j.jmaa.2005.09.078
Senter HF, Dotson WG Jr.: Approximating fixed points of nonexpansive mappings. Proceedings of the American Mathematical Society 1974, 44(2):375-380. 10.1090/S0002-9939-1974-0346608-8
Schu J: Iterative construction of fixed points of strictly pseudocontractive mappings. Applicable Analysis 1991, 40(2-3):67-72. 10.1080/00036819108839994
Acknowledgments
The authors would like to thank the referee and the editor for their careful reading of the manuscript and their many valuable comments and suggestions. This paper was supported by the National Natural Science Foundation of China (Grant no. 10671145).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, C., Zhu, J. Convergence Theorems for Common Fixed Points of Nonself Asymptotically Quasi-Non-Expansive Mappings. Fixed Point Theory Appl 2008, 428241 (2008). https://doi.org/10.1155/2008/428241
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/428241
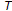 is said to be a nonself asymptotically nonexpansive mapping if there exists a sequence
is said to be a nonself asymptotically nonexpansive mapping if there exists a sequence 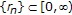 , with
, with 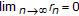 such that
such that 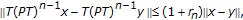
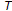 is said to be a nonself uniformly
is said to be a nonself uniformly 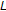 -Lipschitzian mapping if there exists a constant
-Lipschitzian mapping if there exists a constant 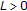 such that
such that 
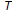 is said to be a nonself asymptotically quasi-non-expansive mapping if
is said to be a nonself asymptotically quasi-non-expansive mapping if  and there exists a sequence
and there exists a sequence 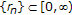 , with
, with  such that
such that 
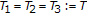 ,
, 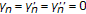 , and
, and  , then scheme (1.6) reduces to the Mann-type iteration (1.4).
, then scheme (1.6) reduces to the Mann-type iteration (1.4).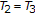 ,
,  , and
, and 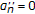 , then scheme (1.6) reduces to the Ishikawa-type iteration (1.5).
, then scheme (1.6) reduces to the Ishikawa-type iteration (1.5).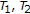 , and
, and 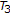 are three self-asymptotically nonexpansive mappings, then scheme (1.6) reduces to the three-step iteration with errors defined by [
are three self-asymptotically nonexpansive mappings, then scheme (1.6) reduces to the three-step iteration with errors defined by [