- Research Article
- Open access
- Published:
Strong Convergence Theorems of the CQ Method for Nonexpansive Semigroups
Fixed Point Theory and Applications volume 2007, Article number: 059735 (2007)
Abstract
Motivated by T. Suzuki, we show strong convergence theorems of the CQ method for nonexpansive semigroups in Hilbert spaces by hybrid method in the mathematical programming. The results presented extend and improve the corresponding results of Kazuhide Nakajo and Wataru Takahashi (2003).
References
Browder FE: Fixed-point theorems for noncompact mappings in Hilbert space. Proceedings of the National Academy of Sciences of the United States of America 1965,53(6):1272–1276. 10.1073/pnas.53.6.1272
Shioji N, Takahashi W: Strong convergence theorems for asymptotically nonexpansive semigroups in Hilbert spaces. Nonlinear Analysis 1998,34(1):87–99. 10.1016/S0362-546X(97)00682-2
Suzuki T: On strong convergence to common fixed points of nonexpansive semigroups in Hilbert spaces. Proceedings of the American Mathematical Society 2003,131(7):2133–2136. 10.1090/S0002-9939-02-06844-2
Xu H-K: A strong convergence theorem for contraction semigroups in Banach spaces. Bulletin of the Australian Mathematical Society 2005,72(3):371–379. 10.1017/S000497270003519X
Chen R, He H: Viscosity approximation of common fixed points of nonexpansive semigroups in Banach space. to appear in Applied Mathematics Letters
Chen R, Zhu Z: Viscosity approximation fixed points for nonexpansive and
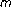 -accretive operators. Fixed Point Theory and Applications 2006, 2006: 10 pages.
-accretive operators. Fixed Point Theory and Applications 2006, 2006: 10 pages.Chen R, Song Y, Zhou H: Convergence theorems for implicit iteration process for a finite family of continuous pseudocontractive mappings. Journal of Mathematical Analysis and Applications 2006,314(2):701–709. 10.1016/j.jmaa.2005.04.018
Yao Y, Chen R: Iterative algorithm for approximating solutions of maximal monotone operators in Hilbert spaces. Fixed Point Theory and Applications 2007, 2007: 8 pages.
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. Journal of Mathematical Analysis and Applications 2003,279(2):372–379. 10.1016/S0022-247X(02)00458-4
Browder FE: Nonexpansive nonlinear operators in a Banach space. Proceedings of the National Academy of Sciences of the United States of America 1965,54(4):1041–1044. 10.1073/pnas.54.4.1041
Martinez-Yanes C, Xu H-K: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Analysis 2006,64(11):2400–2411. 10.1016/j.na.2005.08.018
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Yanagi K: On some fixed point theorems for multivalued mappings. Pacific Journal of Mathematics 1980,87(1):233–240.
Megginson RE: An Introduction to Banach Space Theory, Graduate Texts in Mathematics. Volume 183. Springer, New York, NY, USA; 1998:xx+596.
Takahashi W: Nonlinear Functional Analysis. Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, H., Chen, R. Strong Convergence Theorems of the CQ Method for Nonexpansive Semigroups. Fixed Point Theory Appl 2007, 059735 (2007). https://doi.org/10.1155/2007/59735
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/59735
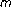 -accretive operators. Fixed Point Theory and Applications 2006, 2006: 10 pages.
-accretive operators. Fixed Point Theory and Applications 2006, 2006: 10 pages.