- Research
- Open access
- Published:
Some results on a general iterative method for k-strictly pseudo-contractive mappings
Fixed Point Theory and Applications volume 2011, Article number: 24 (2011)
Abstract
Let H be a Hilbert space, C be a closed convex subset of H such that C ± C ⊂ C, and T : C → H be a k-strictly pseudo-contractive mapping with F(T) ≠ ∅ for some 0 ≤ k < 1. Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0 and f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let  ,
,  and τ < 1. Let {α
n
} and {β
n
} be sequences in (0, 1). It is proved that under appropriate control conditions on {α
n
} and {β
n
}, the sequence {x
n
} generated by the iterative scheme xn+1= α
n
γf(x
n
) + β
n
x
n
+ ((1 - β
n
)I - α
n
μF)P
C
Sx
n
, where S : C → H is a mapping defined by Sx = kx + (1 - k)Tx and P
C
is the metric projection of H onto C, converges strongly to q ∈ F(T), which solves the variational inequality 〈μFq - γf(q), q - p〉 ≤ 0 for p ∈ F(T).
and τ < 1. Let {α
n
} and {β
n
} be sequences in (0, 1). It is proved that under appropriate control conditions on {α
n
} and {β
n
}, the sequence {x
n
} generated by the iterative scheme xn+1= α
n
γf(x
n
) + β
n
x
n
+ ((1 - β
n
)I - α
n
μF)P
C
Sx
n
, where S : C → H is a mapping defined by Sx = kx + (1 - k)Tx and P
C
is the metric projection of H onto C, converges strongly to q ∈ F(T), which solves the variational inequality 〈μFq - γf(q), q - p〉 ≤ 0 for p ∈ F(T).
MSC: 47H09, 47H05, 47H10, 47J25, 49M05
1 Introduction
Let H be a real Hilbert space and C be a nonempty closed convex subset of H. Recall that a mapping f : C → C is a contraction on C if there exists a constant α ∈ (0, 1) such that ||f(x) - f(y)|| ≤ α||x - y||, x, y ∈ C. A mapping T : C → H is said to be k-strictly pseudo-contractive if there exists a constant k ∈ [0, 1) such that

and F(T) denote the set of fixed points of the mapping T; that is, F(T) = {x ∈ C : Tx = x}.
Note that the class of k-strictly pseudo-contractions includes the class of non-expansive mappings T on C (that is, ||Tx - Ty|| ≤ ||x - y||, x, y ∈ C) as a subclass. That is, T is nonexpansive if and only if T is 0-strictly pseudo-contractive. The mapping T is also said to be pseudo-contractive if k = 1 and T is said to be strongly pseudo-contractive if there exists a constant λ ∈ (0, 1) such that T - λI is pseudo-contractive. Clearly, the class of k-strictly pseudo-contractive mappings falls into the one between classes of nonexpansive mappings and pseudo-contractive mappings. Also we remark that the class of strongly pseudo-contractive mappings is independent of the class of k-strictly pseudo-contractive mappings (see [1–3]). The class of pseudo-contraction is one of the most important classes of mappings among nonlinear mappings. Recently, many authors have been devoting the studies on the problems of finding fixed points for pseudo-contractions, see, for example, [4–7] and references therein.
For nonexpansive mappings, one recent way to study them is to construct the iterative scheme, the so-called viscosity iteration method: more precisely, for a nonexpansive mapping T, a contraction f with the contractive constant α ∈ (0, 1), and α n ∈ (0, 1),

This iterative scheme was first introduced by Moudafi [8].
In particular, under the control conditions on {α n }
(C1) limn→∞α n = 0;
(C2)  ;
;
(C3)  ; or,
; or,
(C4)  ,
,
Xu [9] proved that the sequence {x n } generated by (1.1) converges strongly to a fixed point q of T, which is the unique solution of the following variational inequality:

Recall that an operator A is strongly positive on H if there exists a constant  with the property:
with the property:

In 2006, as the viscosity approximation method, Marino and Xu [10] considered the following iterative method: for a strongly positive bounded linear operator A on H with constant  , a nonexpansive mapping T on H, a contraction f : H → H with the contractive constant α ∈ (0, 1), {α
n
} ⊂ (0, 1) and γ > 0,
, a nonexpansive mapping T on H, a contraction f : H → H with the contractive constant α ∈ (0, 1), {α
n
} ⊂ (0, 1) and γ > 0,

They proved that if the sequence {α n } satisfies the conditions (C1), (C2), and (C3) (or (C1), (C2), and (C4)), then the sequence {x n } generated by (1.2) converges strongly to the unique solution of the variational inequality

which is the optimality condition for the minimization problem

where h is a potential function for γf.
In 2010, in order to improve the corresponding results of Cho et al. [5] as well as Marino and Xu [10] by removing the condition (C3), Jung [6] studied the following composite iterative scheme for the class of k-strictly pseudo-contractive mappings.
Theorem J. Let H be a Hilbert space, C be a closed convex subset of H such that C ± C ⊂ C, T : C → H be a k-strictly pseudo-contractive mapping with F(T) ≠ ∅, for some 0 ≤ k < 1. Let A be a strongly positive bounded linear operator on C with constant and f : C → C be a contraction with the contractive constant α ∈ (0, 1) such that
and f : C → C be a contraction with the contractive constant α ∈ (0, 1) such that . Let {α
n
} and {β
n
} be sequences in (0, 1) satisfying the conditions (C1), (C2) and the condition 0 < lim infn→∞β
n
≤ lim supn→∞β
n
< 1. Let {x
n
} be a sequence in C generated by
. Let {α
n
} and {β
n
} be sequences in (0, 1) satisfying the conditions (C1), (C2) and the condition 0 < lim infn→∞β
n
≤ lim supn→∞β
n
< 1. Let {x
n
} be a sequence in C generated by

where S : C → H is a mapping defined by Sx = kx + (1 - k)Tx and P C is the metric projection of H onto C. Then {x n } converges strongly to a fixed point q of T, which is the unique solution of the following variational inequality related to the linear operator A:

On the other hand, a mapping F : H → H is called κ-Lipschitzian if there exists a positive constant κ such that

F is said to be η-strongly monotone if there exists a positive constant η such that

From the definitions, we note that a strongly positive bounded linear operator A is a ||A||-Lipschitzian and  -strongly monotone operator.
-strongly monotone operator.
In 2001, Yamada [11] introduced the following hybrid iterative method for solving the variational inequality

where F : H → H is a κ-Lipschitzian and η-strongly monotone operator with κ > 0, η > 0,  and S : H → H is a nonexpansive mapping, and proved that if {λ
n
} satisfies appropriate conditions, then the sequence {x
n
} generated by (1.5) converges strongly to the unique solution of the variational inequality
and S : H → H is a nonexpansive mapping, and proved that if {λ
n
} satisfies appropriate conditions, then the sequence {x
n
} generated by (1.5) converges strongly to the unique solution of the variational inequality

In 2010, by combining the iterative method (1.2) with the Yamada's method (1.5), Tian [12] considered the following general iterative method.
Theorem T1. Let H be a Hilbert space, F : H → H be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0, and S : H → H be a nonexpansive mapping with F(S) ≠ ∅. Let f : H → H be a contraction with the contractive constant α ∈ (0, 1). Let and
and . Let {α
n
} be a sequence in (0, 1) satisfying the conditions (C1), (C2) and (C3) (or (C1), (C2) and (C4)). Let {x
n
} be a sequence in H generated by
. Let {α
n
} be a sequence in (0, 1) satisfying the conditions (C1), (C2) and (C3) (or (C1), (C2) and (C4)). Let {x
n
} be a sequence in H generated by

Then {x
n
} converges strongly to a fixed point of S, which is the unique solution of the following variational inequality related to the operator F:
of S, which is the unique solution of the following variational inequality related to the operator F:

In this paper, motivated by the above-mentioned results, we consider the following general iterative scheme for strictly pseudo-contractive mapping: for C a closed convex subset of H such that C ± C ⊂ C, k-strictly pseudo-contractive mapping T : C → H with F(T) ≠ ∅, a contraction f : C → C with the contractive constant α ∈ (0, 1), μ > 0 and {α n }, {β n } ⊂ (0, 1),

where S : C → H is a mapping defined by Sx = kx+(1 - k)Tx, P
C
is the metric projection of H onto C, and F : C → C is a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Under certain different control conditions on {α
n
}, we establish the strong convergence of the sequence {x
n
} generated by (IS) to a fixed point of T, which is a solution of the variational inequality (1.6) related to the operator F. By removing the condition (C3)  on {α
n
}, the main results improve, develop and complement the corresponding results of Tian [12] as well as Cho et al. [5], Jung [6] and Marino and Xu [10]. Our results also improve the corresponding results of Halpern [13], Moudafi [8], Wittmann [14] and Xu [9].
on {α
n
}, the main results improve, develop and complement the corresponding results of Tian [12] as well as Cho et al. [5], Jung [6] and Marino and Xu [10]. Our results also improve the corresponding results of Halpern [13], Moudafi [8], Wittmann [14] and Xu [9].
2 Preliminaries and lemmas
Throughout this paper, when {x n } is a sequence in E, then x n → x (resp., x n ⇀ x) will denote strong (resp., weak) convergence of the sequence {x n } to x.
For every point x ∈ H, there exists a unique nearest point in C, denoted by P C (x), such that

for all y ∈ C. P C is called the metric projection of H onto C. It is well known that P C is nonexpansive.
In a Hilbert space H, we have

It is also well known that H satisfies the Opial condition, that is, for any sequence {x n } with x n ⇀ x, the inequality

holds for every y ∈ H with y ≠ x.
We need the following lemmas for the proof of our main results.
Lemma 2.1[15]. Let H be a Hilbert space and C be a closed convex subset of H. If T is a k-strictly pseudo-contractive mapping on C, then the fixed point set F(T) is closed convex, so that the projection PF(T)is well defined.
Lemma 2.2[15]. Let H be a Hilbert space and C be a closed convex subset of H. Let T : C → H be a k-strictly pseudo-contractive mapping with F(T) ≠ ∅. Then F(P C T) = F (T ).
Lemma 2.3[15]. Let H be a Hilbert space, C be a closed convex subset of H, and T : C → H be a k-strictly pseudo-contractive mapping. Define a mapping S : C → H by Sx = λx + (1 - λ) Tx for all x ∈ C. Then, as λ ∈ [k, 1), S is a nonexpansive mapping such that F(S) = F(T).
The following Lemmas 2.4 and 2.5 can be obtained from the Proposition 2.6 of Acedo and Xu [4].
Lemma 2.4. Let H be a Hilbert space and C be a closed convex subset of H. For any N ≥ 1, assume that for each 1 ≤ i ≤ N, T
i
: C → H is a k
i
-strictly pseudo-contractive mapping for some 0 ≤ k
i
< 1. Assume that is a positive sequence such that
is a positive sequence such that  . Then
. Then  is a nonself-k-strictly pseudo-contractive mapping with k= max{k
i
: 1 ≤ i ≤ N}.
is a nonself-k-strictly pseudo-contractive mapping with k= max{k
i
: 1 ≤ i ≤ N}.
Lemma 2.5. Let and
and be given as in Lemma 2.4. Suppose that
be given as in Lemma 2.4. Suppose that has a common fixed point in C. Then
has a common fixed point in C. Then .
.
Lemma 2.6[16, 17]. Let {s n } be a sequence of non-negative real numbers satisfying

where {λ n }, {δ n } and {r n } satisfy the following conditions:
-
(i)
{λ n } ⊂ [0, 1] and
 ,
,
(ii)lim supn→∞δ
n
≤ 0 or ,
,
-
(iii)
r n ≥ 0 (n ≥ 0),
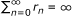 .
.
Then limn→∞s n = 0.
Lemma 2.7[18]. Let {x n } and {z n } be bounded sequences in a Banach space E and {γ n } be a sequence in [0, 1] which satisfies the following condition:

Suppose that xn+1= γ n x n + (1 - γ n )z n for all n ≥ 0 and

Then limn→∞||z n - x n || = 0.
Lemma 2.8. In a Hilbert space H, the following inequality holds:

Lemma 2.9. Let C be a nonempty closed convex subset of a Hilbert space H such that C ± C ⊂ C. Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let and 0 < t < ρ < 1. Then S := ρI - tμF : C → C is a contraction with contractive constant ρ - tτ, where
and 0 < t < ρ < 1. Then S := ρI - tμF : C → C is a contraction with contractive constant ρ - tτ, where with
with .
.
Proof. From (1.3), (1.4) and (2.1), we have

where  , and so
, and so

Hence S is a contraction with contractive constant ρ - tτ. □
3 Main results
We need the following result for the existence of solutions of a certain variational inequality, which is slightly an improvement of Theorem 3.1 of Tian [12].
Theorem T2. Let H be a Hilbert space, C be a closed convex subset of H such that C ± C ⊂ C, and T : C → C be a nonexpansive mapping with F(T) ≠ ∅. Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let ,
,  and τ < 1. Let x
t
be a fixed point of a contraction St ∋ x α tγf (x) + (I - tμF )Tx for t ∈ (0, 1) and
and τ < 1. Let x
t
be a fixed point of a contraction St ∋ x α tγf (x) + (I - tμF )Tx for t ∈ (0, 1) and . Then {x
t
} converges strongly to a fixed point
. Then {x
t
} converges strongly to a fixed point of T as t → 0, which solves the following variational inequality:
of T as t → 0, which solves the following variational inequality:

Equivalently, we have .
.
Now, we study the strong convergence result for a general iterative scheme (IS).
Theorem 3.1. Let H be a Hilbert space, C be a closed convex subset of H such that C ± C ⊂ C, and T : C → H be a k-strictly pseudo-contractive mapping with F(T) ≠ ∅ for some 0 ≤ k < 1. Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let ,
,  and τ < 1. Let f{α
n
} and {β
n
} be sequences in (0, 1) which satisfy the conditions:
and τ < 1. Let f{α
n
} and {β
n
} be sequences in (0, 1) which satisfy the conditions:
(C1) limn→∞α n = 0;
(C2)  ;
;
-
(B)
0 < lim infn→∞ β n ≤ lim supn→∞ βn < 1.
Let {x n } be a sequence in C generated by

where S : C → H is a mapping defined by Sx = kx + (1 - k)Tx and P C is the metric projection of H onto C. Then {x n } converges strongly to q ∈ F(T), which solves the following variational inequality:

Proof. First, from the condition (C1), without loss of generality, we assume that α
n
τ < 1,  and α
n
< (1 - β
n
) for n ≥ 0.
and α
n
< (1 - β
n
) for n ≥ 0.
We divide the proof several steps:
Step 1. We show that  for all n ≥ 0 and all p ∈ F(T) = F(S). Indeed, let p ∈ F(T). Then from Lemma 2.9, we have
for all n ≥ 0 and all p ∈ F(T) = F(S). Indeed, let p ∈ F(T). Then from Lemma 2.9, we have

Using an induction, we have  . Hence, {x
n
} is bounded, and so are {f(x
n
)}, {P
C
Sx
n
} and {FP
C
Sx
n
}.
. Hence, {x
n
} is bounded, and so are {f(x
n
)}, {P
C
Sx
n
} and {FP
C
Sx
n
}.
Step 2. We show that limn→∞||xn+1- x n || = 0. To this show, define

Observe that from the definition of z n ,

Thus, it follows that

From the condition (C1) and (B), it follows that

Hence, by Lemma 2.7, we have

Consequently,

Step 3. We show that limn→∞||x n - P C Sx n || = 0. Indeed, since

we have

that is,

So, from the conditions (C1) and (B) and Step 2, it follows that

Step 4. We show that

where q = limt→0x
t
being x
t
= tγf(x
t
) + (I - tμF )P
C
Sx
t
for 0 < t < 1 and  . We note that from Lemmas 2.2 and 2.3 and Theorem T2, q ∈ F(T) = F(S) and q is a solution of a variational inequality
. We note that from Lemmas 2.2 and 2.3 and Theorem T2, q ∈ F(T) = F(S) and q is a solution of a variational inequality

To show this, we can choose a subsequence  of {x
n
} such that
of {x
n
} such that

Since {x
n
} is bounded, there exists a subsequence  of
of  which converges weakly to w. Without loss of generality, we can assume that
which converges weakly to w. Without loss of generality, we can assume that  . Since ||x
n
- P
C
Sx
n
|| → 0 by Step 3, we obtain w = P
C
Sw. In fact, if w ≠ P
C
Sw, then, by Opial condition,
. Since ||x
n
- P
C
Sx
n
|| → 0 by Step 3, we obtain w = P
C
Sw. In fact, if w ≠ P
C
Sw, then, by Opial condition,

which is a contradiction. Hence w = P C Sw. Since F(P C S) = F(S), from Lemma 2.3, we have w ∈ F(T). Therefore, from (3.1), we conclude that

Step 5. We show that limn→∞||x
n
- q|| = 0, where q = limt→0x
t
being x
t
= tγf (xt) + (I - tμF)P
C
Sx
t
for 0 < t < 1 and  , and q is a solution of a variational inequality
, and q is a solution of a variational inequality

Indeed, from (IS), we have

Applying Lemmas 2.8 and 2.9, we have

that is,

where M = sup{||x
n
- q||2 : n ≥ 0},  and
and

From the conditions (C1) and (C2) and Step 4, it is easy to see that λ
n
→ 0,  , and lim supn→∞δ
n
≤ 0. Hence, by Lemma 2.7, we conclude x
n
→ q as n → ∞. This completes the proof. □
, and lim supn→∞δ
n
≤ 0. Hence, by Lemma 2.7, we conclude x
n
→ q as n → ∞. This completes the proof. □
Remark 3.1. (1) Theorem 3.1 extends and develops Theorem 3.2 of Tian [12] from a nonexpansive mapping to a strictly pseudo-contractive mapping together with removing the condition (C3)  .
.
-
(2)
Theorem 3.1 also generalizes Theorem 2.1 of Jung [6] as well as Theorem 2.1 of Cho et al. [5] and Theorem 3.4 of Marino and Xu [10] from a strongly positive bounded linear operator A to a κ-Lipschitzian and η-strongly monotone operator F.
-
(3)
Theorem 3.1 also improves the corresponding results of Halpern [13], Moudafi [8], Wittmann [14] and Xu [9] as some special cases.
Theorem 3.2. Let H be a Hilbert space, C be a closed convex subset of H such that C ± C ⊂ C, and T
i
: C → H be a k
i
-strictly pseudo-contractive mapping for some 0 ≤ k
i
< 1 and . Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let
. Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let ,
,  and τ < 1. Let {α
n
} and {βn} be sequences in (0, 1) which satisfy the conditions.
and τ < 1. Let {α
n
} and {βn} be sequences in (0, 1) which satisfy the conditions.
(C1) limn→∞α n = 0;
(C2)  ;
;
-
(B)
0 < lim infn→∞ β n ≤ lim supn→∞ β n < 1.
Let {x n } be a sequence in C generated by

where S : C → H is a mapping defined by with k = max{k
i
: 1 ≤ i ≤ N} and {η
i
} is a positive sequence such that
with k = max{k
i
: 1 ≤ i ≤ N} and {η
i
} is a positive sequence such that and P
C
is the metric projection of H onto C. Then {x
n
} converges strongly to q ∈ F(T), which solves the following variational inequality:
and P
C
is the metric projection of H onto C. Then {x
n
} converges strongly to q ∈ F(T), which solves the following variational inequality:

Proof. Define a mapping T : C → H by  . By Lemmas 2.4 and 2.5, we conclude that T : C → H is a k-strictly pseudo-contractive mapping with k = max{k
i
: 1 ≤ i ≤ N} and
. By Lemmas 2.4 and 2.5, we conclude that T : C → H is a k-strictly pseudo-contractive mapping with k = max{k
i
: 1 ≤ i ≤ N} and  . Then the result follows from Theorem 3.1 immediately. □
. Then the result follows from Theorem 3.1 immediately. □
As a direct consequence of Theorem 3.2, we have the following result for nonexpansive mappings (that is, 0-strictly pseudo-contractive mappings).
Theorem 3.3. Let H be a Hilbert space, C be a closed convex subset of H such that C ± C ⊂ C,  be a finite family of nonexpansive mappings with
be a finite family of nonexpansive mappings with . Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let
. Let F : C → C be a κ-Lipschitzian and η-strongly monotone operator with κ > 0 and η > 0. Let f : C → C be a contraction with the contractive constant α ∈ (0, 1). Let ,
,  and τ < 1. Let {α
n
} and {βn} be sequences in (0, 1) which satisfy the conditions.
and τ < 1. Let {α
n
} and {βn} be sequences in (0, 1) which satisfy the conditions.
(C1) limn→∞α n = 0;
(C2)  ;
;
-
(B)
0 < lim infn→∞ β n ≤ lim supn→∞ β n < 1.
Let {x n } be a sequence in C generated by

where is a positive sequence such that
is a positive sequence such that and P
C
is the metric projection of H onto C. Then {x
n
} converges strongly to a common fixed point q of
and P
C
is the metric projection of H onto C. Then {x
n
} converges strongly to a common fixed point q of , which solves the following variational inequality:
, which solves the following variational inequality:

Remark 3.2. (1) Theorems 3.2 and 3.3 also generalize Theorems 2.2 and 2.4 of Jung [6] from a strongly positive bounded linear operator A to a κ-Lipschitzian and η-strongly monotone operator F.
-
(2)
Theorems 3.2 and 3.3 also improve and complement the corresponding results of Cho et al. [5] by removing the condition (C3)
 together with using a κ-Lipschitzian and η-strongly monotone operator F.
together with using a κ-Lipschitzian and η-strongly monotone operator F. -
(3)
As in [19], we also can establish the result for a countable family {T i } of k i -strict pseudo-contractive mappings with 0 ≤ k i < 1.
References
Browder FE: Fixed point theorems for noncompact mappings. Proc Natl Acad Sci USA 1965, 53: 1272–1276. 10.1073/pnas.53.6.1272
Browder FE: Convergence of approximants to fixed points of nonexpansive nonlinear mappings in Banach spaces. Arch Ration Mech Anal 1967, 24: 82–90.
Browder FE, Petryshn WV: Construction of fixed points of nonlinear mappings Hilbert space. J Math Anal Appl 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Acedo GL, Xu HK: Iterative methods for strictly pseudo-contractions in Hilbert space. Nonlinear Anal 2007, 67: 2258–2271. 10.1016/j.na.2006.08.036
Cho YJ, Kang SM, Qin X: Some results on k -strictly pseudo-contractive mappings in Hilbert spaces. Nonlinear Anal 2009, 70: 1956–1964. 10.1016/j.na.2008.02.094
Jung JS: Strong convergence of iterative methods for k -strictly pseudo-contractive mappings in Hilbert spaces. Appl Math Comput 2010, 215: 3746–3753. 10.1016/j.amc.2009.11.015
Morales CH, Jung JS: Convergence of paths for pseudo-contractive mappings in Banach spaces. Proc Am Math Soc 2000, 128: 3411–3419. 10.1090/S0002-9939-00-05573-8
Moudafi A: Viscosity approximation methods for fixed-points problems. J Math Anal Appl 2000, 241: 46–55. 10.1006/jmaa.1999.6615
Xu HK: Viscosity approximation methods for nonexpansive mappings. J Math Anal Appl 2004, 298: 279–291. 10.1016/j.jmaa.2004.04.059
Marino G, Xu HX: A general iterative method for nonexpansive mappings in Hilbert spaces. J Math Anal Appl 2006, 318: 43–52. 10.1016/j.jmaa.2005.05.028
Yamada I: The hybrid steepest descent for the variational inequality problems over the intersection of fixed points sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications. Edited by: Butnariu D, Censor Y, Reich S. Elservier, New York; 2001:473–504.
Tian M: A general itewrative algorithm for nonexpansive mappings in Hilbert spaces. Nonlinear Anal 2010, 73: 689–694. 10.1016/j.na.2010.03.058
Halpern B: Fixed points of nonexpansive maps. Bull Am Math Soc 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Wittmann R: Approximation of fixed points of nonexpansive mappings. Arch Math 1992, 58: 486–491. 10.1007/BF01190119
Zhou H: Convergence theorems of fixed points for k -strict pseudo-contractions in Hilbert spaces. Nonlinear Anal 2008, 69: 456–462. 10.1016/j.na.2007.05.032
Liu LS: Iterative processes with errors for nonlinear strongly accretive mappings in Banach spaces. J Math Anal Appl 1995, 194: 114–125. 10.1006/jmaa.1995.1289
Xu HK: Iterative algorithms for nonlinear operators. J Lond Math Soc 2002, 66: 240–256. 10.1112/S0024610702003332
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one parameter nonexpansive semigroups without Bochner integral. J Math Anal Appl 2005, 305: 227–239. 10.1016/j.jmaa.2004.11.017
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Anal 2007, 67: 2350–2360. 10.1016/j.na.2006.08.032
Acknowledgements
This study was supported by research funds from Dong-A University.
Author information
Authors and Affiliations
Corresponding author
Additional information
4 Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jung, J.S. Some results on a general iterative method for k-strictly pseudo-contractive mappings. Fixed Point Theory Appl 2011, 24 (2011). https://doi.org/10.1186/1687-1812-2011-24
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-24
 .
.