- Research Article
- Open access
- Published:
Common Fixed Point Theorem for Four Non-Self Mappings in Cone Metric Spaces
Fixed Point Theory and Applications volume 2010, Article number: 983802 (2010)
Abstract
We extend a common fixed point theorem of Radenovic and Rhoades for four non-self-mappings in cone metric spaces.
1. Introduction and Preliminaries
Recently, Huang and Zhang [1] generalized the concept of a metric space, replacing the set of real numbers by ordered Banach space and obtained some fixed point theorems for mappings satisfying different contractive conditions. Subsequently, the study of fixed point theorems in such spaces is followed by some other mathematicians; see [2–8]. The aim of this paper is to prove a common fixed point theorem for four non-self-mappings on cone metric spaces in which the cone need not be normal. This result generalizes the result of Radenović and Rhoades [5].
Consistent with Huang and Zhang [1], the following definitions and results will be needed in the sequel.
Let  be a real Banach space. A subset
be a real Banach space. A subset  of
of  is called a cone if and only if
is called a cone if and only if
(a) is closed, nonempty and
is closed, nonempty and  ;
;
(b) ,
,  ,
,  implies
implies  ;
;
(c) .
.
Given a cone  , we define a partial ordering
, we define a partial ordering  with respect to
with respect to  by
by  if and only if
if and only if  . A cone
. A cone  is called normal if there is a number
is called normal if there is a number  such that for all
such that for all  ,
,

The least positive number satisfying the above inequality is called the normal constant of  , while
, while  stands for
stands for  (interior of
(interior of  ).
).
Definition 1.1 (see [1]).
Let  be a nonempty set. Suppose that the mapping
be a nonempty set. Suppose that the mapping  satisfies
satisfies
(d1) for all
for all  and
and  if and only if
if and only if  ;
;
(d2) for all
for all  ;
;
(d3) for all
for all  .
.
Then  is called a cone metric on
is called a cone metric on  , and
, and  is called a cone metric space.
is called a cone metric space.
The concept of a cone metric space is more general than that of a metric space.
Definition 1.2 (see [1]).
Let  be a cone metric space. One says that
be a cone metric space. One says that  is
is
-
(e)
a Cauchy sequence if for every
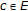 with
with  , there is an
, there is an 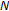 such that for all
such that for all  ,
,  ;
; -
(f)
a Convergent sequence if for every
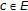 with
with  , there is an
, there is an 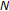 such that for all
such that for all 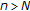 ,
, 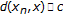 for some fixed
for some fixed 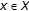 .
.
A cone metric space  is said to be complete if every Cauchy sequence in
is said to be complete if every Cauchy sequence in  is convergent in
is convergent in  . It is known that
. It is known that  converges to
converges to  if and only if
if and only if  as
as  . It is a Cauchy sequence if and only if
. It is a Cauchy sequence if and only if  .
.
Remark 1.3 (see [9]).
Let  be an ordered Banach (normed) space. Then
be an ordered Banach (normed) space. Then  is an interior point of
is an interior point of  if and only if
if and only if  is a neighborhood of
is a neighborhood of  .
.
Corollary 1.4 (see [10]).
-
(1)
If
 and
and  , then
, then  .Indeed,
.Indeed,  implies
implies  .
.
(2)If  and
and  , then
, then  .Indeed,
.Indeed,  implies
implies  .
.
-
(3)
If
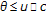 for each
for each 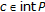 , then
, then  .
.
If  ,
,  , and
, and  , then there exists an
, then there exists an  such that for all
such that for all  we have
we have  .
.
If  is a real Banach space with cone
is a real Banach space with cone  and if
and if  where
where  and
and  , then
, then  .
.
We find it convenient to introduce the following definition.
Definition 1.7 (see [5]).
Let  be a complete cone metric space and
be a complete cone metric space and  a nonempty closed subset of
a nonempty closed subset of  , and
, and  satisfying
satisfying

where

for all  ,
,  ,
,  , then
, then  is called a generalized
is called a generalized  -contractive mapping of
-contractive mapping of  into
into  .
.
Definition 1.8 (see [2]).
Let  and
and  be self-maps on a set
be self-maps on a set  (i.e.,
(i.e.,  ). If
). If  for some
for some  in
in  , then
, then  is called a coincidence point of
is called a coincidence point of  and
and  , and
, and  is called a point of coincidence of
is called a point of coincidence of  and
and  . Self-maps
. Self-maps  and
and  are said to be weakly compatible if they commute at their coincidence point; that is, if
are said to be weakly compatible if they commute at their coincidence point; that is, if  for some
for some  , then
, then  .
.
2. Main Result
The following theorem is Radenović and Rhoades [5] generalization of Imdad and Kumar's [12] result in cone metric spaces.
Theorem 2.1.
Let  be a complete cone metric space and
be a complete cone metric space and  a nonempty closed subset of
a nonempty closed subset of  such that for each
such that for each  and
and  there exists a point
there exists a point  (the boundary of
(the boundary of  ) such that
) such that

Suppose that  are such that
are such that  is a generalized
is a generalized  -contractive mapping of
-contractive mapping of  into
into  , and
, and
(i) ,
,
(ii) ,
,
(iii) is closed in
is closed in  .
.
Then the pair  has a coincidence point. Moreover, if pair
has a coincidence point. Moreover, if pair  is weakly compatible, then
is weakly compatible, then  and
and  have a unique common fixed point.
have a unique common fixed point.
The purpose of this paper is to extend the above theorem for four non-self-mappings in cone metric spaces. We begin with the following definition.
Definition 2.2.
Let  be a complete cone metric space and
be a complete cone metric space and  a nonempty closed subset of
a nonempty closed subset of  , and
, and  satisfying
satisfying

where

for all  ,
,  ,
,  , then
, then  is called a generalized
is called a generalized  -contractive mappings pair of
-contractive mappings pair of  into
into  .
.
Notice that by setting  and
and  in (2.2), one deduces the slightly generalized form of (1.3).
in (2.2), one deduces the slightly generalized form of (1.3).
We state and prove our main result as follows.
Theorem 2.3.
Let  be a complete cone metric space and
be a complete cone metric space and  a nonempty closed subset of
a nonempty closed subset of  such that for each
such that for each  and
and  there exists a point
there exists a point  (the boundary of
(the boundary of  ) such that
) such that

Suppose that  are such that
are such that  is a generalized
is a generalized  -contractive mappings pair of
-contractive mappings pair of  into
into  , and
, and
(I) ,
,
(II) ,
,
(III) and
and  (or
(or  and
and  ) are closed in
) are closed in  .Then
.Then
(IV) has a point of coincidence,
has a point of coincidence,
(V) has a point of coincidence.
has a point of coincidence.
Moreover, if  and
and  are weakly compatible pairs, then
are weakly compatible pairs, then  ,
,  ,
,  , and
, and  have a unique common fixed point.
have a unique common fixed point.
Proof.
Firstly, we proceed to construct two sequences  and
and  in the following way.
in the following way.
Let  be arbitrary. Then (due to
be arbitrary. Then (due to  ) there exists a point
) there exists a point  such that
such that  . Since
. Since  , one concludes that
, one concludes that  . Thus, there exists
. Thus, there exists  such that
such that  . Since
. Since  there exists a point
there exists a point  such that
such that

Suppose that  . Then
. Then  which implies that there exists a point
which implies that there exists a point  such that
such that  . Otherwise, if
. Otherwise, if  , then there exists a point
, then there exists a point  such that
such that

Since  there exists a point
there exists a point  with
with  , so that
, so that

Let  be such that
be such that  . Thus, repeating the foregoing arguments, one obtains two sequences
. Thus, repeating the foregoing arguments, one obtains two sequences  and
and  such that
such that
(a) ,
,  ,
,
(b) or
or  ,
,

(c) or
or  ,
,

We denote that

Note that  , as if
, as if  , then
, then  , and one infers that
, and one infers that  which implies that
which implies that  . Hence
. Hence  . Similarly, one can argue that
. Similarly, one can argue that  .
.
Now, we distinguish the following three cases.
Case 1.
If  , then from (2.2)
, then from (2.2)

where

Clearly, there are infinite many  such that at least one of the following four cases holds:
such that at least one of the following four cases holds:
-
(1)
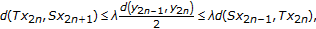 (2.13)
(2.13)
-
(2)
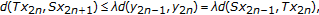 (2.14)
(2.14)
-
(3)
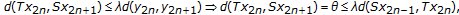 (2.15)
(2.15)
-
(4)
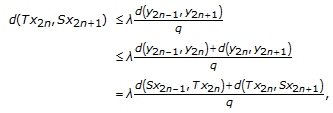 (2.16)
(2.16)
which implies  , that is,
, that is,

From (1), (2), (3), and ( ) it follows that
) it follows that

Similarly, if  , we have
, we have

If  , we have
, we have

Case 2.
If  , then
, then  and
and

which in turn yields

and hence

Now, proceeding as in Case 1, we have that (2.18) holds.
If  , then
, then  . We show that
. We show that

Using (2.21), we get

By noting that  , one can conclude that
, one can conclude that

in view of Case 1.
Thus,

and we proved (2.24).
Case 3.
If  , then
, then  . We show that
. We show that

Since  , then
, then

From this, we get

By noting that  , one can conclude that
, one can conclude that

in view of Case 1.
Thus,

and we proved (2.28).
Similarly, if  , then
, then  , and
, and

From this, we have

By noting that  , one can conclude that
, one can conclude that

in view of Case 1.
Thus, in all Cases 1–3, there exists  such that
such that

and there exists  such that
such that

Following the procedure of Assad and Kirk [13], it can easily be shown by induction that, for  , there exists
, there exists  such that
such that

From (2.38) and by the triangle inequality, for  , we have
, we have

From Remark 1.5 and Corollary 1.4(1),  .
.
Thus, the sequence  is a Cauchy sequence. Then, as noted in [14], there exists at least one subsequence
is a Cauchy sequence. Then, as noted in [14], there exists at least one subsequence  or
or  which is contained in
which is contained in  or
or  , respectively, and finds its limit
, respectively, and finds its limit  Furthermore, subsequences
Furthermore, subsequences  and
and  both converge to
both converge to  as
as  is a closed subset of complete cone metric space
is a closed subset of complete cone metric space  . We assume that there exists a subsequence
. We assume that there exists a subsequence  for each
for each  , then
, then  . Since
. Since  as well as
as well as  are closed in
are closed in  , and
, and  is Cauchy in
is Cauchy in  , it converges to a point
, it converges to a point  . Let
. Let  , then
, then  . Similarly,
. Similarly,  a subsequence of Cauchy sequence
a subsequence of Cauchy sequence  also converges to
also converges to  as
as  is closed. Using (2.2), one can write
is closed. Using (2.2), one can write

where

Let  . Clearly at least one of the following four cases holds for infinitely many
. Clearly at least one of the following four cases holds for infinitely many  :
:
-
(1)
 (2.42)
(2.42)
-
(2)
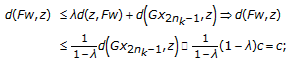 (2.43)
(2.43)
-
(3)
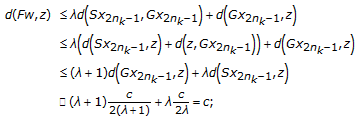 (2.44)
(2.44)
-
(4)
 (2.45)
(2.45)
In all cases we obtain  for each
for each  . Using Corollary 1.4(3) it follows that
. Using Corollary 1.4(3) it follows that  or
or  . Thus,
. Thus,  , that is,
, that is,  is a coincidence point of
is a coincidence point of  ,
,  .
.
Further, since Cauchy sequence  converges to
converges to  and
and  ,
,  , there exists
, there exists  such that
such that  . Again using (2.2), we get
. Again using (2.2), we get

where

Hence, we get the following cases:

Since  , using Remark 1.6 and Corollary 1.4(3), it follows that
, using Remark 1.6 and Corollary 1.4(3), it follows that  ; therefore,
; therefore,  , that is,
, that is,  is a coincidence point of
is a coincidence point of  .
.
In case  and
and  are closed in
are closed in  ,
,  or
or  . The analogous arguments establish (IV) and (V). If we assume that there exists a subsequence
. The analogous arguments establish (IV) and (V). If we assume that there exists a subsequence  with
with  as well
as well  being closed in
being closed in  , then noting that
, then noting that  is a Cauchy sequence in
is a Cauchy sequence in  , foregoing arguments establish (IV) and (V).
, foregoing arguments establish (IV) and (V).
Suppose now that  and
and  are weakly compatible pairs, then
are weakly compatible pairs, then

Then, from (2.2),

where

Hence, we get the following cases:

Since  , using Remark 1.6 and Corollary 1.4(3), it follows that
, using Remark 1.6 and Corollary 1.4(3), it follows that  . Thus,
. Thus,  .
.
Similarly, we can prove that  . Therefore
. Therefore  , that is,
, that is,  is a common fixed point of
is a common fixed point of  ,
,  ,
,  , and
, and  .
.
Uniqueness of the common fixed point follows easily from (2.2).
The following example shows that in general  ,
,  ,
,  , and
, and  satisfying the hypotheses of Theorem 2.3 need not have a common coincidence justifying two separate conclusions (IV) and (V).
satisfying the hypotheses of Theorem 2.3 need not have a common coincidence justifying two separate conclusions (IV) and (V).
Example 2.4.
Let  ,
,  ,
,  ,
,  , and
, and  defined by
defined by  , where
, where  is a fixed function, for example,
is a fixed function, for example,  . Then
. Then  is a complete cone metric space with a nonnormal cone having the nonempty interior. Define
is a complete cone metric space with a nonnormal cone having the nonempty interior. Define  ,
,  ,
,  , and
, and  as
as

Since  . Clearly, for each
. Clearly, for each  and
and  there exists a point
there exists a point  such that
such that  . Further,
. Further,  ,
,  ,
,  , and
, and  ,
,  ,
,  , and
, and  are closed in
are closed in  .
.
Also,

Moreover, for each  ,
,

that is, (2.2) is satisfied with  .
.
Evidently,  and
and  . Notice that two separate coincidence points are not common fixed points as
. Notice that two separate coincidence points are not common fixed points as  and
and  , which shows necessity of weakly compatible property in Theorem 2.3.
, which shows necessity of weakly compatible property in Theorem 2.3.
Next, we furnish an illustrate example in support of our result. In doing so, we are essentially inspired by Imdad and Kumar [12].
Example 2.5.
Let  ,
,  ,
,  , and
, and  defined by
defined by  , where
, where  is a fixed function, for example,
is a fixed function, for example,  . Then
. Then  is a complete cone metric space with a nonnormal cone having the nonempty interior. Define
is a complete cone metric space with a nonnormal cone having the nonempty interior. Define  ,
,  ,
,  , and
, and  as
as

Since  . Clearly, for each
. Clearly, for each  and
and  there exists a point
there exists a point  such that
such that  . Further,
. Further,  ,
,  , and
, and  .
.
Also,

Moreover, if  and
and  , then
, then

Next, if  , then
, then

Finally, if  , then
, then

Therefore, condition (2.2) is satisfied if we choose  . Moreover
. Moreover  is a point of coincidence as
is a point of coincidence as  as well as
as well as  whereas both the pairs
whereas both the pairs  and
and  are weakly compatible as
are weakly compatible as  and
and  . Also,
. Also,  ,
,  ,
,  , and
, and  are closed in
are closed in  . Thus, all the conditions of Theorem 2.3 are satisfied and
. Thus, all the conditions of Theorem 2.3 are satisfied and  is the unique common fixed point of
is the unique common fixed point of  ,
,  ,
,  , and
, and  . One may note that
. One may note that  is also a point of coincidence for both the pairs
is also a point of coincidence for both the pairs  and
and  .
.
Remark 2.6.
-
(1)
Setting
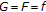 and
and 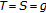 in Theorem 2.3, one deduces Theorem 2.1 due to [5].
in Theorem 2.3, one deduces Theorem 2.1 due to [5].
-
(2)
Setting
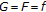 and
and  in Theorem 2.3, we obtain the following result.
in Theorem 2.3, we obtain the following result.
Corollary 2.7.
Let  be a complete cone metric space and
be a complete cone metric space and  a nonempty closed subset of
a nonempty closed subset of  such that for each
such that for each  and
and  there exists a point
there exists a point  (the boundary of
(the boundary of  ) such that
) such that

Suppose that  satisfies the condition
satisfies the condition

where

for all  ,
,  ,
,  , and
, and  has the additional property that for each
has the additional property that for each  ,
,  ,
,  has a unique fixed point.
has a unique fixed point.
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. Journal of Mathematical Analysis and Applications 2008,341(1):416–420. 10.1016/j.jmaa.2007.09.070
Abbas M, Rhoades BE: Fixed and periodic point results in cone metric spaces. Applied Mathematics Letters 2009,22(4):511–515. 10.1016/j.aml.2008.07.001
Ilić D, Rakočević V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Radenović S, Rhoades BE: Fixed point theorem for two non-self mappings in cone metric spaces. Computers & Mathematics with Applications 2009,57(10):1701–1707. 10.1016/j.camwa.2009.03.058
Rezapour Sh, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Vetro P: Common fixed points in cone metric spaces. Rendiconti del Circolo Matematico di Palermo 2007,56(3):464–468. 10.1007/BF03032097
Wardowski D: Endpoints and fixed points of set-valued contractions in cone metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(1–2):512–516. 10.1016/j.na.2008.10.089
Wong YC, Ng KF: Partially Ordered Topological Vector Spaces, Oxford Mathematical Monographs. Clarendon Press, Oxford, UK; 1973:x+217.
Rezapour Sh: A review on topological properties of cone metric spaces. In Analysis, Topology and Applications (ATA '08). , Vrnjacka Banja, Serbia; May-June 2008.
Jungck G, Radenović S, Radojević S, Rakočević V: Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory and Applications 2009, 2009:-13.
Imdad M, Kumar S: Rhoades-type fixed-point theorems for a pair of nonself mappings. Computers & Mathematics with Applications 2003,46(5–6):919–927. 10.1016/S0898-1221(03)90153-2
Assad NA, Kirk WA: Fixed point theorems for set-valued mappings of contractive type. Pacific Journal of Mathematics 1972, 43: 553–562.
Hadžić O, Gajić L: Coincidence points for set-valued mappings in convex metric spaces. Univerzitet u Novom Sadu. Zbornik Radova Prirodno-Matematičkog Fakulteta. Serija za Matemati 1986,16(1):13–25.
Acknowledgments
The authors would like to express their sincere appreciation to the referees for their very helpful suggestions and many kind comments. This project was supported by the National Natural Science Foundation of China (10461007 and 10761007) and supported partly by the Provincial Natural Science Foundation of Jiangxi, China (2008GZS0076 and 2009GZS0019).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, X., Zhu, C. & Wen, X. Common Fixed Point Theorem for Four Non-Self Mappings in Cone Metric Spaces. Fixed Point Theory Appl 2010, 983802 (2010). https://doi.org/10.1155/2010/983802
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/983802
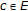 with
with  , there is an
, there is an 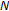 such that for all
such that for all  ,
,  ;
;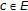 with
with  , there is an
, there is an 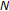 such that for all
such that for all 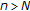 ,
, 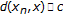 for some fixed
for some fixed 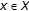 .
. and
and  , then
, then  .Indeed,
.Indeed,  implies
implies  .
.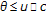 for each
for each 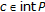 , then
, then  .
.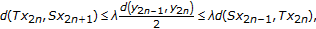
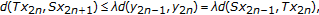
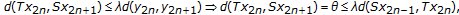
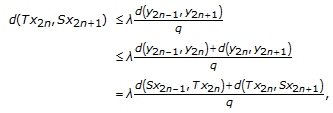

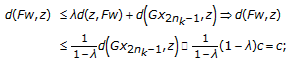

 and
and  in Theorem 2.3, one deduces Theorem 2.1 due to [
in Theorem 2.3, one deduces Theorem 2.1 due to [ and
and  in Theorem 2.3, we obtain the following result.
in Theorem 2.3, we obtain the following result.