- Research Article
- Open access
- Published:
Viscosity Approximation to Common Fixed Points of Families of Nonexpansive Mappings with Weakly Contractive Mappings
Fixed Point Theory and Applications volume 2010, Article number: 476913 (2010)
Abstract
Let X be a reflexive Banach space which has a weakly sequentially continuous duality mapping. In this paper, we consider the following viscosity approximation sequence  , where
, where 
 (0, 1),
(0, 1),  is a uniformly asymptotically regular sequence, and f is a weakly contractive mapping. Strong convergence of the sequence
is a uniformly asymptotically regular sequence, and f is a weakly contractive mapping. Strong convergence of the sequence  is proved.
is proved.
1. Introduction
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  . Recall that a self-mapping
. Recall that a self-mapping  is nonexpansive if
is nonexpansive if

Alber and Guerre-Delabriere [1] defined the weakly contractive maps in Hilbert spaces, and Rhoades [2] showed that the result of [1] is also valid in the complete metric spaces as follows.
Definition 1.1.
Let  be a complete metric space. A mapping
be a complete metric space. A mapping  is called weakly contractive if
is called weakly contractive if

where  and
and  is a continuous and nondecreasing function such that
is a continuous and nondecreasing function such that  if and only if
if and only if  and
and  .
.
Theorem 1.2.
Let  be a weakly contractive mapping, where
be a weakly contractive mapping, where  is a complete metric space, then
is a complete metric space, then  has a unique fixed point.
has a unique fixed point.
In 2007, Song and Chen [3] considered the iterative sequence

They proved the strong convergence of the iterative sequence  , where
, where  is a contraction mapping and
is a contraction mapping and  is a uniformly asymptotically regular sequence of nonexpansive mappings in a reflexive Banach space
is a uniformly asymptotically regular sequence of nonexpansive mappings in a reflexive Banach space  , as follows.
, as follows.
Theorem 1.3 (see [3, Theorem  ]).
]).
Let  be a reflexive Banach space which admits a weakly sequentially continuous duality mapping
be a reflexive Banach space which admits a weakly sequentially continuous duality mapping  from
from  to
to  . Suppose that
. Suppose that  is a nonempty closed convex subset of
is a nonempty closed convex subset of  and
and  is a uniformly asymptotically regular sequence of nonexpansive mappings from
is a uniformly asymptotically regular sequence of nonexpansive mappings from  into itself such that
into itself such that

where  . Let
. Let  be defined by (1.3) and
be defined by (1.3) and  , such that
, such that  . Then as
. Then as  , the sequence
, the sequence  converges strongly to
converges strongly to  , such that
, such that  is the unique solution, in
is the unique solution, in  , to the variational inequality:
, to the variational inequality:

In this paper, inspired by the above results, strong convergence of sequence (1.3) is proved, where  is a weakly contractive mapping.
is a weakly contractive mapping.
2. Preliminaries
A Banach space  is called strictly convex if
is called strictly convex if

A Banach space  is called uniformly convex, if for all
is called uniformly convex, if for all  there exist
there exist  such that
such that

The following results are well known which can be founded in [4].
(1)A uniformly convex Banach space  is reflexive and strictly convex.
is reflexive and strictly convex.
(2)If  is a nonempty convex subset of a strictly convex Banach space
is a nonempty convex subset of a strictly convex Banach space  and
and  is a nonexpansive mapping, then the fixed point set
is a nonexpansive mapping, then the fixed point set  of
of  is a closed convex subset of
is a closed convex subset of  .
.
By a gauge function we mean a continuous strictly increasing function  defined on
defined on  such that
such that  and
and  . The mapping
. The mapping  defined by
defined by

is called the duality mapping with gauge function  . In the case where
. In the case where  then
then  which is the normalized duality mapping.
which is the normalized duality mapping.
Proposition 2.1 (see [5]).
-
(1)
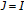 if and only if
if and only if 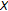 is a Hilbert space.
is a Hilbert space. -
(2)
 is surjective if and only if
is surjective if and only if 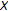 is reflexive.
is reflexive. -
(3)
 for all
for all  ; in particular
; in particular  , for all
, for all  .
.
We say that a Banach space  has a weakly sequentially continuous duality mapping if there exists a gauge function
has a weakly sequentially continuous duality mapping if there exists a gauge function  such that the duality mapping
such that the duality mapping  is single-valued and continuous from the weak topology to the wea
is single-valued and continuous from the weak topology to the wea topology of
topology of  .
.
We recall [6] that a Banach space  is said to satisfy Opial's condition, if for any sequence
is said to satisfy Opial's condition, if for any sequence  in
in  , which converges weakly to
, which converges weakly to  , we have
, we have

It is known [7] that any separable Banach space can be equivalently renormed such that it satisfies Opial's condition. A space with a weakly sequentially continuous duality mapping is easily seen to satisfy Opial's condition [8].
Lemma 2.2 (see [9, Lemma  ]).
]).
Let  be a Banach space satisfying Opial's condition and
be a Banach space satisfying Opial's condition and  a nonempty, closed, and convex subset of
a nonempty, closed, and convex subset of  . Suppose that
. Suppose that  is a nonexpansive mapping. Then
is a nonexpansive mapping. Then  is demiclosed at zero, that is, if
is demiclosed at zero, that is, if  is a sequence in
is a sequence in  which converges weakly to
which converges weakly to  and if the sequence
and if the sequence  converges strongly to zero, then
converges strongly to zero, then  .
.
Definition 2.3 (see [3]).
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  and
and  , where
, where  . Then the mapping sequence
. Then the mapping sequence  is called uniformly asymptotically regular on
is called uniformly asymptotically regular on  , if for all
, if for all  and any bounded subset
and any bounded subset  of
of  we have
we have

3. Main Result
In this section, we prove a new version of Theorem 1.3.
Theorem 3.1.
Let  be a reflexive Banach space which admits a weakly sequentially continuous duality mapping
be a reflexive Banach space which admits a weakly sequentially continuous duality mapping  from
from  to
to  . Suppose that
. Suppose that  is a nonempty closed convex subset of
is a nonempty closed convex subset of  and
and  is a uniformly asymptotically regular sequence of nonexpansive mappings such that
is a uniformly asymptotically regular sequence of nonexpansive mappings such that

Let  be a weakly contractive mapping. Suppose that
be a weakly contractive mapping. Suppose that  is a sequence of positive numbers in
is a sequence of positive numbers in  satisfying
satisfying  . Assume that
. Assume that  is defined by the following iterative process:
is defined by the following iterative process:

Then the above sequence  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  such that
such that  is the unique solution, in
is the unique solution, in  , to the variational inequality
, to the variational inequality

Proof.
Step 1.
We prove the uniqueness of the solution to the variational inequality (3.3). Suppose that  are distinct solutions to (3.3). Then
are distinct solutions to (3.3). Then

By adding up the above relations, we get

Thus  , hence
, hence  . We denote by
. We denote by  the unique solution, in
the unique solution, in  , to (3.3).
, to (3.3).
Step 2.
We show that the sequence  is bounded. Let
is bounded. Let  ; from (3.2) we get then that
; from (3.2) we get then that

Thus

or

Therefore  is bounded.
is bounded.
Step 3.
We prove that  , for all
, for all  . Since the sequence
. Since the sequence  is bounded, so
is bounded, so  and
and  are bounded. Hence
are bounded. Hence  , thus
, thus  . Let
. Let  be a bounded subset of
be a bounded subset of  which contains
which contains  . Since the sequence
. Since the sequence  is uniformly asymptotically regular, we can obtain
is uniformly asymptotically regular, we can obtain

Let  , then
, then

Hence  , for all
, for all  .
.
Step 4.
We show that the sequence  is sequentially compact. Since
is sequentially compact. Since  is reflexive and
is reflexive and  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  such that
such that  is weakly convergent to
is weakly convergent to  as
as  . Since
. Since  for all
for all  , by Lemma 2.2, we have
, by Lemma 2.2, we have  for all
for all  . Thus
. Thus  .
.
Step 2 implies that

Hence

Since  is single valued and weakly sequentially continuous from
is single valued and weakly sequentially continuous from  to
to  , we have
, we have

Thus  . Hence the sequence
. Hence the sequence  is sequentially compact.
is sequentially compact.
Step 5.
We now prove that  is a solution to the variational inequality (3.3). Suppose that
is a solution to the variational inequality (3.3). Suppose that  , then
, then

Hence

Since  as
as  , we have
, we have

as  . Hence
. Hence

Thus  is a solution to the variational inequality (3.3). By uniqueness,
is a solution to the variational inequality (3.3). By uniqueness,  . Since the sequence
. Since the sequence  is sequentially compact and each cluster point of it is equal to
is sequentially compact and each cluster point of it is equal to  , then
, then  as
as  . The proof is completed.
. The proof is completed.
It is known that [10, Example  ] in a uniformly convex Banach space
] in a uniformly convex Banach space  , the Cesàro means
, the Cesàro means  for nonexpansive mapping
for nonexpansive mapping  is uniformly asymptotically regular. So we have the following corollary, which is a new version of [10, Theorem
is uniformly asymptotically regular. So we have the following corollary, which is a new version of [10, Theorem  ].
].
Corollary 3.2.
Let  be a real uniformly convex Banach space which admits a weakly sequentially continuous duality mapping
be a real uniformly convex Banach space which admits a weakly sequentially continuous duality mapping  from
from  to
to  and
and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Suppose that
. Suppose that  is a nonexpansive mapping,
is a nonexpansive mapping,  and
and  is a weakly contractive mapping. Let
is a weakly contractive mapping. Let  be defined by
be defined by

where  and
and  . Then as
. Then as  ,
,  converges strongly to a fixed point
converges strongly to a fixed point  of
of  , where
, where  is the unique solution in
is the unique solution in  to the following variational inequality:
to the following variational inequality:

References
Alber YaI, Guerre-Delabriere S: Principle of weakly contractive maps in Hilbert spaces. In New Results in Operator Theory and Its Applications, Operator Theory: Advances and Applications. Volume 98. Birkhäuser, Basel, Switzerland; 1997:7–22.
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Analysis: Theory, Methods & Applications 2001, 47: 2683–2693. 10.1016/S0362-546X(01)00388-1
Song Y, Chen R: Iterative approximation to common fixed points of nonexpansive mapping sequences in reflexive Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2007,66(3):591–603. 10.1016/j.na.2005.12.004
Takahashi W: Nonlinear Functional Analysis. Fixed Point Theory and Its Applications. Yokohama, Yokohama, Japan; 2000:iv+276.
Xu ZB, Roach GF: Characteristic inequalities of uniformly convex and uniformly smooth Banach spaces. Journal of Mathematical Analysis and Applications 1991,157(1):189–210. 10.1016/0022-247X(91)90144-O
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
van Dulst D: Equivalent norms and the fixed point property for nonexpansive mappings. Journal of the London Mathematical Society 1982,25(1):139–144. 10.1112/jlms/s2-25.1.139
Browder FE: Convergence theorems for sequences of nonlinear operators in Banach spaces. Mathematische Zeitschrift 1967, 100: 201–225. 10.1007/BF01109805
Górnicki J: Weak convergence theorems for asymptotically nonexpansive mappings in uniformly convex Banach spaces. Commentationes Mathematicae Universitatis Carolinae 1989,30(2):249–252.
Song Y, Chen R: Viscosity approximate methods to Cesàro means for non-expansive mappings. Applied Mathematics and Computation 2007,186(2):1120–1128. 10.1016/j.amc.2006.08.054
Acknowledgment
A. Razani would like to thank the School of Mathematics of the Institute for Research in Fundamental Sciences, Teheran, Iran for supporting this paper (Grant no.89470126).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Razani, A., Homaeipour, S. Viscosity Approximation to Common Fixed Points of Families of Nonexpansive Mappings with Weakly Contractive Mappings. Fixed Point Theory Appl 2010, 476913 (2010). https://doi.org/10.1155/2010/476913
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/476913
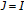 if and only if
if and only if 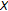 is a Hilbert space.
is a Hilbert space. is surjective if and only if
is surjective if and only if 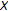 is reflexive.
is reflexive. for all
for all  ; in particular
; in particular  , for all
, for all  .
.