- Research Article
- Open access
- Published:
The Fixed Point Property of Unital Abelian Banach Algebras
Fixed Point Theory and Applications volume 2010, Article number: 362829 (2010)
Abstract
We give a general condition for infinite dimensional unital Abelian Banach algebras to fail the fixed point property. Examples of those algebras are given including the algebras of continuous functions on compact sets.
1. Introduction
Let  be a Banach space. A mapping
be a Banach space. A mapping  is nonexpansive if
is nonexpansive if

for each  The fixed point set of
The fixed point set of  is
is  We say that the space
We say that the space  has the fixed point property (or weak fixed point property) if for every nonempty bounded closed convex (or weakly compact convex, resp.) subset
has the fixed point property (or weak fixed point property) if for every nonempty bounded closed convex (or weakly compact convex, resp.) subset  of
of  and every nonexpansive mapping
and every nonexpansive mapping  we have
we have  One of the central goals in fixed point theory is to solve the problem: which Banach spaces have the (weak) fixed point property?
One of the central goals in fixed point theory is to solve the problem: which Banach spaces have the (weak) fixed point property?
For weak fixed point property, Alspach [1] exhibited a weakly compact convex subset  of the Lebesgue space
of the Lebesgue space  and an isometry
and an isometry  without a fixed point, proving that the space
without a fixed point, proving that the space  does not have the weak fixed point property. Lau et al. [2] proved the following results.
does not have the weak fixed point property. Lau et al. [2] proved the following results.
Theorem 1.1.
Let  be a locally compact Hausdorff space. If
be a locally compact Hausdorff space. If  has the weak fixed point property, then X is dispersed.
has the weak fixed point property, then X is dispersed.
Corollary.
Let  be a locally compact group. Then the
be a locally compact group. Then the  -algebra
-algebra  has the weak fixed point property if and only if
has the weak fixed point property if and only if  is discrete.
is discrete.
Corollary.
A von Neumann algebra  has the weak fixed point property if and only if
has the weak fixed point property if and only if  is finite dimensional.
is finite dimensional.
Continuing in this direction, Benavides and Pineda [3] developed the concept of  -almost weak orthogonality in the Banach lattice
-almost weak orthogonality in the Banach lattice  and obtained the results.
and obtained the results.
Theorem.
Let  be a
be a  -almost weakly orthogonal closed subspace of
-almost weakly orthogonal closed subspace of  where
where  is a metrizable compact space. Then
is a metrizable compact space. Then  has the weak fixed point property.
has the weak fixed point property.
Theorem.
Let  be a metrizable compact space. Then, the following conditions are all equivalent:
be a metrizable compact space. Then, the following conditions are all equivalent:
(1) is
is  -almost weakly orthogonal,
-almost weakly orthogonal,
(2) is
is  -weakly orthogonal,
-weakly orthogonal,
(3)
Corollary.
Let  be a compact set with
be a compact set with  Then
Then  has the weak fixed point property.
has the weak fixed point property.
As for the fixed point property, Dhompongsa et al. [4] showed that a  -algebra has the fixed point property if and only if it is finite dimensional. In this paper, we approach the question on the fixed point property from the opposite direction by identifying unital abelian Banach algebras which fail to have the fixed point property. As consequences, we obtain results on the algebra of continuous functions
-algebra has the fixed point property if and only if it is finite dimensional. In this paper, we approach the question on the fixed point property from the opposite direction by identifying unital abelian Banach algebras which fail to have the fixed point property. As consequences, we obtain results on the algebra of continuous functions  where
where  is a compact set, and there is a unital abelian subalgebra of the algebra
is a compact set, and there is a unital abelian subalgebra of the algebra  which does not have the fixed point property and does not contain the space
which does not have the fixed point property and does not contain the space 
2. Preliminaries and Lemmas
The fields of real and complex numbers are denoted by  and
and  , respectively. The symbol
, respectively. The symbol  denotes a field that can be either
denotes a field that can be either  or
or  The elements of
The elements of  are called scalars.
are called scalars.
An element  in a unital algebra
in a unital algebra  is said to be invertible if there is an element
is said to be invertible if there is an element  in
in  such that
such that

In this case  is unique and written
is unique and written 
We define the spectrum of an element  of a unital algebra
of a unital algebra  over
over  to be the set
to be the set

The spectral radius of  is defined to be
is defined to be

We note that a subalgbra of a normed algebra is itself a normed algebra with the norm got by restriction. The closure of a subalgebra is a subalgebra. A closed subalgebra of a Banach algebra is a Banach algebra. If  is a family of subalgebras of an algebra
is a family of subalgebras of an algebra  then
then  is a subalgebra also. Hence, for any subset
is a subalgebra also. Hence, for any subset  of
of  there is the smallest subalgebra
there is the smallest subalgebra  of
of  containing
containing  This algebra is called the subalgebra of
This algebra is called the subalgebra of  generated by
generated by  If
If  is the singleton
is the singleton  then
then  is the linear span of all powers
is the linear span of all powers  of
of  If
If  is a normed algebra, the closed algebra
is a normed algebra, the closed algebra  generated by a set
generated by a set  is the smallest closed subalgebra containing
is the smallest closed subalgebra containing  We can see that
We can see that 
We denote by  the Banach algebra of continuous functions from a topological space
the Banach algebra of continuous functions from a topological space  to
to  with the sup-norm
with the sup-norm

The following theorems are known as the Stone-Weierstrass approximation theorem for  and
and  respectively. For the details, the readers are referred to [5].
respectively. For the details, the readers are referred to [5].
Theorem.
Let  be a subalgebra of
be a subalgebra of  such that
such that
(1°) separates the points of
separates the points of 
(2°) annihilates no point of
annihilates no point of 
Then  is dense in
is dense in 
Theorem.
Let  be a compact space,
be a compact space,  a subalgebra of
a subalgebra of  such that
such that
(1°) separates the points of
separates the points of 
(2°) annihilates no point of
annihilates no point of 
(3°) implies that the conjugate
implies that the conjugate  of
of  is in
is in 
Then  is dense in
is dense in 
A character on a unital algebra  over
over  is a nonzero homomorphism
is a nonzero homomorphism  We denote by
We denote by  the set of characters on
the set of characters on  Note that if
Note that if  is a unital abelian complex Banach algebra, then
is a unital abelian complex Banach algebra, then

for each  (see [6]).
(see [6]).
Remark.
It is unknown if (2.5) is valid whenever  Equation (2.5) obviously does not hold for a space
Equation (2.5) obviously does not hold for a space  with
with  as the following example shows.
as the following example shows.
Example 2.4.
Let  be considered as a real unital abelian Banach algebra under ordinary complex multiplication and whose norm is the absolute value. We have
be considered as a real unital abelian Banach algebra under ordinary complex multiplication and whose norm is the absolute value. We have  Indeed, assume to the contrary that there is a non-zero homomorphism
Indeed, assume to the contrary that there is a non-zero homomorphism  on
on  and
and  so
so

Thus  so
so  is not a real number, which is a contradiction.
is not a real number, which is a contradiction.
Since  so
so  but
but 
We consider throughout this paper on Banach algebras  for which
for which  and satisfy (2.5).
and satisfy (2.5).
If  is a unital abelian Banach algebra, it follows from Proposition 2.5 that
is a unital abelian Banach algebra, it follows from Proposition 2.5 that  is contained in the closed unit ball of
is contained in the closed unit ball of  We endow
We endow  with the relative weak* topology and call the topological space
with the relative weak* topology and call the topological space  the character space of
the character space of 
Detailed proofs of the following propositions can be found in [6].
Proposition.
Let  be a unital abelian Banach algebra. If
be a unital abelian Banach algebra. If  then
then 
Proposition.
If  is a unital Banach algebra, then
is a unital Banach algebra, then  is compact.
is compact.
If  is a unital abelian Banach algebra, and
is a unital abelian Banach algebra, and  we define a continuous function
we define a continuous function  by
by

We call  the Gelfand transform of
the Gelfand transform of  and the homomorphism
and the homomorphism

is called the Gelfand representation.
The following two lemmas, Lemmas 2.7 and 2.10, will be used to prove our main theorem.
Lemma.
Let  be a unital abelian real Banach algebra with
be a unital abelian real Banach algebra with

Then one has the following:
(i)the Gelfand representation  is a bounded isomorphism,
is a bounded isomorphism,
(ii)the inverse  is also a bounded isomorphism.
is also a bounded isomorphism.
Proof.
-
(i)
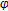 is injective since
is injective since  implies
implies 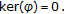 It is easily checked that
It is easily checked that  is a bounded homomorphism, and
is a bounded homomorphism, and  is a subalgebra of
is a subalgebra of 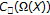 separating the points of
separating the points of 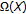 , and having the property that for any
, and having the property that for any 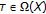 there is an element
there is an element  such that
such that 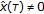 . In order to use the Stone-Weierstrass theorem to show that
. In order to use the Stone-Weierstrass theorem to show that 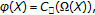 we shall show that
we shall show that 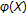 is closed. We show that
is closed. We show that  is closed by showing that
is closed by showing that  is complete. Let
is complete. Let 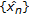 be a Cauchy sequence in
be a Cauchy sequence in  First, we show that the sequence
First, we show that the sequence 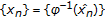 is Cauchy. Assume on the contrary that
is Cauchy. Assume on the contrary that 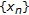 is not Cauchy. Thus there exists
is not Cauchy. Thus there exists 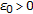 and subsequences
and subsequences 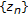 and
and 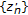 of
of 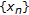 such that
such that 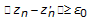 (2.10)
(2.10)
for each  Write
Write  then
then  for each
for each  But
But  is Cauchy, and so we have
is Cauchy, and so we have  Thus
Thus

which is a contradiction. Hence  must be Cauchy and so
must be Cauchy and so  for some
for some  Since
Since  for each
for each  so
so  Thus
Thus  is complete. The Stone-Weierstrass theorem can be applied to conclude that
is complete. The Stone-Weierstrass theorem can be applied to conclude that  is surjective.
is surjective.
-
(ii)
follows from the open mapping theorem.
Remark 2.8.
-
(i)
Lemma 2.7 tells us that if
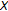 is a unital abelian real Banach algebra with property
is a unital abelian real Banach algebra with property 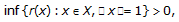 (2.12)
(2.12)
then  and
and  are homeomorphic and isomorphic under
are homeomorphic and isomorphic under  Hence if we would like to consider the convergence of a sequence
Hence if we would like to consider the convergence of a sequence  in
in  we could look at the convergence of the corresponding sequence
we could look at the convergence of the corresponding sequence 
-
(ii)
Property (2.12) clearly implies the semisimplicity property (
 ) but the following example shows that it is stronger.
) but the following example shows that it is stronger.
Example.
Let  denote the Banach algebra of complex-valued absolutely summable functions on the group of integers
denote the Banach algebra of complex-valued absolutely summable functions on the group of integers  under convolution regarded as a real Banach algebra and let
under convolution regarded as a real Banach algebra and let  be the real subalgebra of
be the real subalgebra of  consisting of those functions that satisfy
consisting of those functions that satisfy  Then the maximal ideal space of
Then the maximal ideal space of  equals
equals  and the Gelfand transform is precisely the Fourier transform which maps
and the Gelfand transform is precisely the Fourier transform which maps  into the real Banach algebra
into the real Banach algebra  of continuous real-valued functions on
of continuous real-valued functions on  under pointwise multiplication and maximum norm. Although the image of the Fourier transform is dense, it is clearly not all of
under pointwise multiplication and maximum norm. Although the image of the Fourier transform is dense, it is clearly not all of  since it is simply the real-valued functions in the Wiener space which consists of complex-valued functions whose Fourier series are absolutely summable. Therefore Lemma 2.7 shows that
since it is simply the real-valued functions in the Wiener space which consists of complex-valued functions whose Fourier series are absolutely summable. Therefore Lemma 2.7 shows that  does not have Property (2.12).
does not have Property (2.12).
Lemma.
Let  be an infinite dimensional unital abelian real Banach algebra with
be an infinite dimensional unital abelian real Banach algebra with

Then one has the following:
(i)  is an infinite set,
is an infinite set,
(ii)if there exists a bounded sequence  in
in  which contains no convergent subsequences and such that
which contains no convergent subsequences and such that  is finite for each
is finite for each  then there is an element
then there is an element  with
with

(iii)there is an element  such that
such that  is an infinite set,
is an infinite set,
-
(iv)
there exists a sequence
 in
in  such that
such that 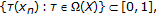 for each
for each 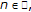 and
and  is a sequence of nonempty pairwise disjoint subsets of
is a sequence of nonempty pairwise disjoint subsets of 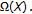
Proof.
Let  be an infinite dimensional unital abelian real Banach algebra with
be an infinite dimensional unital abelian real Banach algebra with

(i)If suffices to show that if  is a finite set, for then the closed unit ball
is a finite set, for then the closed unit ball  of
of  is compact, and this will lead to us a contradiction. Let
is compact, and this will lead to us a contradiction. Let  be a finite set, say
be a finite set, say  , and let
, and let  be a sequence in
be a sequence in 
Since the sequences  are bounded, we can choose a subsequence
are bounded, we can choose a subsequence  of
of  such that
such that  for each
for each 
Define  by
by  Thus there exists
Thus there exists  such that
such that  and consequently,
and consequently,  since
since

and  for each
for each 
So  is a subsequence of
is a subsequence of  such that
such that  By Remark 2.8,
By Remark 2.8,  where
where  Thus
Thus  is compact.
is compact.
-
(ii)
Let
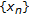 be a bounded sequence in
be a bounded sequence in 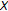 which has no convergent subsequences and suppose that the set
which has no convergent subsequences and suppose that the set  is finite for each
is finite for each 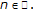 By Remark 2.8, we will consider
By Remark 2.8, we will consider 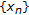 as a sequence of Gelfand transforms
as a sequence of Gelfand transforms 
First, we show that we can write

where  is closed,
is closed,  are all closed and open, and
are all closed and open, and  is a partition of
is a partition of  For each
For each  write
write

Define

Note that  are all closed and open. Since
are all closed and open. Since  is a partition of
is a partition of  for each
for each 
 is a partition of
is a partition of  There are two cases to be considered.
There are two cases to be considered.
Case 1 ( is infinite).
is infinite).
Thus there exists  such that
such that

is an infinite set. Similarly, there exists  such that
such that

is an infinite set. Continuing in this process we obtain a sequence of the sets  such that
such that

is an infinite set, for each 
Write

Thus  are all closed and open, and
are all closed and open, and

where  is a nonempty closed set since
is a nonempty closed set since  is compact. And since
is compact. And since  has infinite elements, we can see that there exists a subsequence
has infinite elements, we can see that there exists a subsequence  of
of  such that
such that  and
and  for each
for each 
Hence we have

and  is a partition of
is a partition of 
Case 2 ( ).
).
To show that this case leads to a contradiction, we first observe that if  are in the same
are in the same  then
then

for each  Write
Write  if
if  There exists a subsequence
There exists a subsequence  of
of  such that for each
such that for each 

for some  Define a Gelfand transform
Define a Gelfand transform  by
by  if
if  Since
Since

so  which is a contradiction.
which is a contradiction.
Now we conclude that

where  is closed,
is closed,  is closed and open for each
is closed and open for each  and
and  is a partition of
is a partition of  Define a map
Define a map  by
by

We can check that the inverse image of each closed set in  is closed. Therefore,
is closed. Therefore,  is an element in
is an element in  say
say  with
with

-
(iii)
Assume to the contrary that
 is finite for each
is finite for each 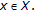 Since
Since 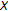 is infinite dimensional, so, as
is infinite dimensional, so, as  is noncompact, there exists a bounded sequence
is noncompact, there exists a bounded sequence 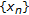 in
in  which has no convergent subsequences. Hence
which has no convergent subsequences. Hence  is finite for each
is finite for each  It follows from (ii) that
It follows from (ii) that

for some  which is the contradiction.
which is the contradiction.
-
(iv)
From (iii), there is an element
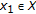 such that
such that 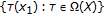 is an infinite set. We can choose
is an infinite set. We can choose 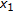 so that there exists a strictly decreasing sequence
so that there exists a strictly decreasing sequence  such that
such that

and  for some
for some  Define a continuous function
Define a continuous function  to be linear on
to be linear on  and on
and on  joining the points
joining the points  and
and  and
and  Put
Put  for some
for some  and define a continuous function
and define a continuous function  similar to the way we construct
similar to the way we construct  The left part of
The left part of  is the line joining the point
is the line joining the point  and
and  and
and  Then put
Then put  for some
for some  Continuing in this process we obtain a sequence of points
Continuing in this process we obtain a sequence of points  such that
such that  for each
for each  and
and  is a sequence of nonempty pairwise disjoint subsets of
is a sequence of nonempty pairwise disjoint subsets of  We then obtain the required result.
We then obtain the required result.
3. Main Theorem
Now we prove our main theorem.
Theorem.
Let  be an infinite dimensional unital abelian real Banach algebra satisfying each of the following:
be an infinite dimensional unital abelian real Banach algebra satisfying each of the following:
(i)if  is such that
is such that  for each
for each  then
then 
(ii)
Then  does not have fixed point property.
does not have fixed point property.
Proof.
Let  be an infinite dimensional unital abelian real Banach algebra satisfying (i) and (ii). Assume to the contrary that
be an infinite dimensional unital abelian real Banach algebra satisfying (i) and (ii). Assume to the contrary that  has fixed point property. From Lemma 2.10(iv), there exists a sequence
has fixed point property. From Lemma 2.10(iv), there exists a sequence  in
in  such that
such that

for each  and
and  is a sequence of nonempty pairwise disjoint subsets of
is a sequence of nonempty pairwise disjoint subsets of  Write
Write  and define
and define  by
by

where

It follows from (i) that  is a nonexpansive mapping on the bounded closed convex set
is a nonexpansive mapping on the bounded closed convex set  for each
for each  Indeed,
Indeed,  is bounded since
is bounded since

for each  It follows that
It follows that  has a fixed point, say
has a fixed point, say  for each
for each  Since
Since  thus
thus  and then
and then

for each  Since
Since  are pairwise disjoint, so
are pairwise disjoint, so  if
if  Hence
Hence  has no convergent subsequences. From Lemma 2.7,
has no convergent subsequences. From Lemma 2.7,  has no convergent subsequences too. It follows from the existence of
has no convergent subsequences too. It follows from the existence of  and Lemma 2.10 (ii) that there exists an element
and Lemma 2.10 (ii) that there exists an element  in
in  with
with

Write  Define
Define  by
by

where

By (i),  is a nonexpansive mapping on the bounded closed convex set
is a nonexpansive mapping on the bounded closed convex set  Thus
Thus  has a fixed point, say
has a fixed point, say  that is,
that is,  Thus
Thus  Consequently,
Consequently,

The set  is open in
is open in  since
since  is continuous. Also the set
is continuous. Also the set  is open in
is open in  for each
for each  since
since  is continuous. Thus,
is continuous. Thus,

is an open covering of  This leads to a contradiction, since
This leads to a contradiction, since  is compact.
is compact.
From the above theorem we have the following.
Corollary 3.2.
Let  be a compact Hausdorff topological space. If
be a compact Hausdorff topological space. If  is infinite dimensional, then
is infinite dimensional, then  fails to have the fixed point property.
fails to have the fixed point property.
Proof.
 satisfies (i), (ii) in Theorem 3.1. Indeed, if
satisfies (i), (ii) in Theorem 3.1. Indeed, if  is such that
is such that  for each
for each  then
then  for each
for each  Hence
Hence  And since
And since

so 
Let  denote the Banach algebra of all real bounded sequences with the sup-norm. The following two propositions tell us that there is a subalgebra of
denote the Banach algebra of all real bounded sequences with the sup-norm. The following two propositions tell us that there is a subalgebra of  which does not contain
which does not contain  but fails to have the fixed point property.
but fails to have the fixed point property.
Proposition 3.3.
If  is a subset of
is a subset of  which contains an infinite bounded sequence and the identity, then the Banach subalgebra
which contains an infinite bounded sequence and the identity, then the Banach subalgebra  of
of  generated by
generated by  fails to have the fixed point property.
fails to have the fixed point property.
Proof.
Let  be a subset of
be a subset of  which contains an infinite bounded sequence
which contains an infinite bounded sequence  and the identity. It follows that
and the identity. It follows that  is unital and abelian.
is unital and abelian.  is infinite dimensional, since the set
is infinite dimensional, since the set  is a linearly independent subset of
is a linearly independent subset of  Next, we show that
Next, we show that  satisfies (i) and (ii) in Theorem 3.1.
satisfies (i) and (ii) in Theorem 3.1.
Let  be such that
be such that  and
and  for each
for each  Define
Define  by
by

for each  Hence
Hence  for each
for each  and thus
and thus

for each  Clearly,
Clearly, 
Since for each  we have
we have

so  Now it follows from Theorem 3.1 that
Now it follows from Theorem 3.1 that  doesn't have the fixed point property.
doesn't have the fixed point property.
Proposition.
Let  with
with  Then the Banach subalgebra
Then the Banach subalgebra  of
of  generated by the identity and
generated by the identity and  does not contain the space
does not contain the space 
Proof.
We have

If  then
then  for some
for some  and
and  It follows that
It follows that  for each
for each  Write
Write  Hence
Hence

for each  From the above inequality, and since
From the above inequality, and since  is arbitrary, we can see that the sequence
is arbitrary, we can see that the sequence  does not lie in
does not lie in 
4. Results on Complex Banach Algebras
Let  be a unital abelian complex Banach algebra. Consider the following condition.
be a unital abelian complex Banach algebra. Consider the following condition.
(A)
For each
 there exists an element
there exists an element
 such that
such that
 for each
for each

If  satisfies condition (A), then
satisfies condition (A), then  is a subspace of
is a subspace of  which is closed under the complex conjugation. By using the Stone-Weierstrass theorem for the complex Banach algebra
which is closed under the complex conjugation. By using the Stone-Weierstrass theorem for the complex Banach algebra  and following the proof of Lemma 2.7, we obtain the following result.
and following the proof of Lemma 2.7, we obtain the following result.
Lemma.
Let  be a unital abelian complex Banach algebra satisfying (A) and
be a unital abelian complex Banach algebra satisfying (A) and

Then one has the following:
(i)the Gelfand representation  is a bounded isomorphism,
is a bounded isomorphism,
(ii)the inverse  is also a bounded isomorphism.
is also a bounded isomorphism.
Using Lemma 4.1 we obtain the complex counterpart of Lemma 2.10.
Lemma.
Let  be an infinite dimensional unital abelian complex Banach algebra satisfying (A) and
be an infinite dimensional unital abelian complex Banach algebra satisfying (A) and

Then one has the following:
(i) is an infinite set,
is an infinite set,
(ii)if there exists a bounded sequence  in
in  which contains no convergent subsequences and such that
which contains no convergent subsequences and such that  is finite for each
is finite for each  then there is an element
then there is an element  with
with

(iii)there is an element  such that
such that  is an infinite set,
is an infinite set,
(iv)there exists a sequence  in
in  such that
such that  for each
for each  and
and  is a sequence of nonempty pairwise disjoint subsets of
is a sequence of nonempty pairwise disjoint subsets of 
By using Lemmas 4.1 and 4.2, and by following the proof of Theorem 3.1, we get the following theorem.
Theorem.
Let  be an infinite dimensional unital abelian complex Banach algebra satisfying (A) and each of the following:
be an infinite dimensional unital abelian complex Banach algebra satisfying (A) and each of the following:
-
(i)
if
 is such that
is such that 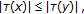 for each
for each 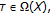 then
then 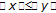 ,
,
(ii)
Then  does not have the fixed point property.
does not have the fixed point property.
References
Alspach DE: A fixed point free nonexpansive map. Proceedings of the American Mathematical Society 1981,82(3):423–424. 10.1090/S0002-9939-1981-0612733-0
Lau AT-M, Mah PF, Ülger A: Fixed point property and normal structure for Banach spaces associated to locally compact groups. Proceedings of the American Mathematical Society 1997,125(7):2021–2027. 10.1090/S0002-9939-97-03773-8
Domínguez Benavides T, Japón Pineda MA: Fixed points of nonexpansive mappings in spaces of continuous functions. Proceedings of the American Mathematical Society 2005,133(10):3037–3046. 10.1090/S0002-9939-05-08149-9
Dhompongsa S, Fupinwong W, Lawton W: Fixed point properties of -algebras. submitted
Berberian SK: Fundamentals of Real Analysis. Springer, New York, NY, USA; 1996.
Murphy GJ: C∗-Algebras and Operator Theory. Academic Press, Boston, Mass, USA; 1990:x+286.
Acknowledgments
The authors would like to express their thanks to the referees for valuable comments, especially, to whom that provides them Remark 2.8(ii) and Example 2.9 for completeness. This work was supported by the Thailand Research Fund, grant BRG50800016.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fupinwong, W., Dhompongsa, S. The Fixed Point Property of Unital Abelian Banach Algebras. Fixed Point Theory Appl 2010, 362829 (2010). https://doi.org/10.1155/2010/362829
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/362829
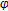 is injective since
is injective since  implies
implies 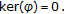 It is easily checked that
It is easily checked that  is a bounded homomorphism, and
is a bounded homomorphism, and  is a subalgebra of
is a subalgebra of 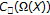 separating the points of
separating the points of 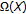 , and having the property that for any
, and having the property that for any 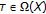 there is an element
there is an element  such that
such that 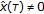 . In order to use the Stone-Weierstrass theorem to show that
. In order to use the Stone-Weierstrass theorem to show that 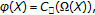 we shall show that
we shall show that 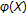 is closed. We show that
is closed. We show that  is closed by showing that
is closed by showing that  is complete. Let
is complete. Let 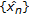 be a Cauchy sequence in
be a Cauchy sequence in  First, we show that the sequence
First, we show that the sequence 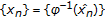 is Cauchy. Assume on the contrary that
is Cauchy. Assume on the contrary that 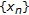 is not Cauchy. Thus there exists
is not Cauchy. Thus there exists 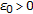 and subsequences
and subsequences 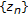 and
and 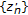 of
of 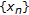 such that
such that 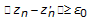
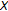 is a unital abelian real Banach algebra with property
is a unital abelian real Banach algebra with property 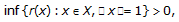
 ) but the following example shows that it is stronger.
) but the following example shows that it is stronger. in
in  such that
such that 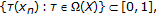 for each
for each 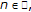 and
and  is a sequence of nonempty pairwise disjoint subsets of
is a sequence of nonempty pairwise disjoint subsets of 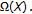
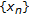 be a bounded sequence in
be a bounded sequence in 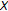 which has no convergent subsequences and suppose that the set
which has no convergent subsequences and suppose that the set  is finite for each
is finite for each 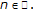 By Remark 2.8, we will consider
By Remark 2.8, we will consider 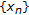 as a sequence of Gelfand transforms
as a sequence of Gelfand transforms 
 is finite for each
is finite for each 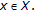 Since
Since 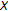 is infinite dimensional, so, as
is infinite dimensional, so, as  is noncompact, there exists a bounded sequence
is noncompact, there exists a bounded sequence 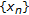 in
in  which has no convergent subsequences. Hence
which has no convergent subsequences. Hence  is finite for each
is finite for each  It follows from (ii) that
It follows from (ii) that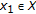 such that
such that 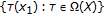 is an infinite set. We can choose
is an infinite set. We can choose 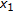 so that there exists a strictly decreasing sequence
so that there exists a strictly decreasing sequence  such that
such that is such that
is such that 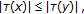 for each
for each 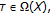 then
then 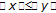 ,
,