- Research Article
- Open access
- Published:
Ergodic Retractions for Families of Asymptotically Nonexpansive Mappings
Fixed Point Theory and Applications volume 2010, Article number: 281362 (2010)
Abstract
We prove some theorems for the existence of ergodic retractions onto the set of common fixed points of a family of asymptotically nonexpansive mappings. Our results extend corresponding results of Benavides and Ramírez (2001), and Li and Sims (2002).
1. Introduction
Let  be a Banach space and
be a Banach space and  a nonempty closed and convex subset of
a nonempty closed and convex subset of  . We recall some definitions.
. We recall some definitions.
Definition 1.1.
A mapping  is said to be
is said to be
(i)nonexpansive if

(ii)asymptotically nonexpansive if there exists a sequence  of positive numbers satisfying the property
of positive numbers satisfying the property  and
and

(iii)of asymptotically nonexpansive type if for each  in
in  , we have
, we have

(iv)weakly asymptotically nonexpansive if it satisfies the condition

(v)retraction if  . A subset
. A subset  of
of  is called a nonexpansive retract of
is called a nonexpansive retract of  if either
if either  or there exists a retraction of
or there exists a retraction of  onto
onto  which is a nonexpansive mapping.
which is a nonexpansive mapping.
Definition 1.2.
We say that a nonempty closed convex subset  of
of  satisfies property
satisfies property  with respect to
with respect to
(i)a mapping  if
if  for every
for every  where
where

(ii)a semigroup of mappings  if
if  for every
for every  where
where

Obviously,  itself verifies
itself verifies  .
.
Definition 1.3.
-
(i)
A mapping
 is said to satisfy the
is said to satisfy the 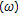 -fixed point property (
-fixed point property ( -fpp) if
-fpp) if  has a fixed point in every nonempty closed convex subset
has a fixed point in every nonempty closed convex subset  of
of  which satisfies
which satisfies 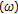 with respect to
with respect to  .
. -
(ii)
A semigroup
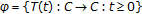 is said to satisfy the
is said to satisfy the  -fpp if
-fpp if 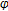 has a common fixed point in every nonempty closed convex subset
has a common fixed point in every nonempty closed convex subset  of
of  which satisfies
which satisfies 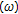 with respect to the semigroup
with respect to the semigroup 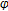 .
. -
(iii)
A family
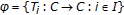 is said to satisfy the
is said to satisfy the 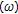 -fpp if
-fpp if 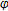 has a common fixed point in every nonempty closed convex subset
has a common fixed point in every nonempty closed convex subset  of
of  which satisfies
which satisfies 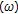 with respect to each
with respect to each  .
.
In 1965, Kirk [1] proved that if  is a weakly compact convex subset of a Banach space with normal structure, then every nonexpansive mapping
is a weakly compact convex subset of a Banach space with normal structure, then every nonexpansive mapping  has a fixed point. (A nonempty convex subset
has a fixed point. (A nonempty convex subset  of a normed linear space is said to have normal structure if each bounded convex subset
of a normed linear space is said to have normal structure if each bounded convex subset  of
of  consisting of more than one point contains a nondiametral point). Goebel and Kirk [2] proved that if
consisting of more than one point contains a nondiametral point). Goebel and Kirk [2] proved that if  is assumed to be uniformly convex, then every asymptotically nonexpansive self-mapping
is assumed to be uniformly convex, then every asymptotically nonexpansive self-mapping  of
of  has a fixed point. This was extended to mappings of asymptotically nonexpansive type by Kirk in [3]. However, whether normal structure implies the existence of fixed points for mappings of asymptotically nonexpansive type is a natural and still open question. Li and Sims [4] proved the following fixed point result in the case that
has a fixed point. This was extended to mappings of asymptotically nonexpansive type by Kirk in [3]. However, whether normal structure implies the existence of fixed points for mappings of asymptotically nonexpansive type is a natural and still open question. Li and Sims [4] proved the following fixed point result in the case that  has uniform normal structure (It is known that a space with uniform normal structure is reflexive and that all uniformly convex or uniformly smooth Banach spaces have uniform normal structure).
has uniform normal structure (It is known that a space with uniform normal structure is reflexive and that all uniformly convex or uniformly smooth Banach spaces have uniform normal structure).
Theorem 1.4.
Suppose  is a Banach space with uniform normal structure;
is a Banach space with uniform normal structure;  is a nonempty bounded subset of
is a nonempty bounded subset of  . Then
. Then
(i)every continuous and asymptotically nonexpansive type mapping  satisfies
satisfies  -fpp;
-fpp;
(ii)every semigroup  of asymptotically nonexpansive type mappings on
of asymptotically nonexpansive type mappings on  such that
such that  is continuous on
is continuous on  for each
for each  satisfies
satisfies  -fpp.
-fpp.
On the other hand, Bruck [5] initiated the study of the structure of the fixed point set  in a general Banach space
in a general Banach space  : if
: if  is a weakly compact convex subset of
is a weakly compact convex subset of  and
and  is nonexpansive and satisfies a conditional fixed point property, then
is nonexpansive and satisfies a conditional fixed point property, then  is a nonexpansive retract of
is a nonexpansive retract of  . The same author [6] used this fact to derive the existence of fixed points for a commuting family of nonexpansive mappings. See, for example, [7, 8] for some related results.
. The same author [6] used this fact to derive the existence of fixed points for a commuting family of nonexpansive mappings. See, for example, [7, 8] for some related results.
Benavides and Ramírez [9] studied the structure of the set of fixed points for (weakly) asymptotically nonexpansive mappings.
Theorem 1.5.
Let  be a Banach space and
be a Banach space and  a nonempty weakly compact convex subset of
a nonempty weakly compact convex subset of  . Assume that every asymptotically nonexpansive self-mapping of
. Assume that every asymptotically nonexpansive self-mapping of  satisfies the
satisfies the  -fpp. Then for any commuting family
-fpp. Then for any commuting family  of asymptotically nonexpansive self-mappings of
of asymptotically nonexpansive self-mappings of  , the common fixed point set of
, the common fixed point set of  ,
,  , is a nonempty nonexpansive retract of
, is a nonempty nonexpansive retract of  .
.
In this paper, we prove some theorems to guarantee the existence of nonexpansive retractions onto the common fixed points of some families of (weakly) asymptotically nonexpansive (type) mappings. The results obtained in this paper extend in some sense, for example, Theorems 1.4 and 1.5, above.
2. Nonexpansive Retractions for Families of Weakly Asymptotically Nonexpansive Mappings
Theorem 2.1.
Let  be a nonempty weakly compact convex subset of a Banach space
be a nonempty weakly compact convex subset of a Banach space  , and
, and  a family of weakly asymptotically nonexpansive mappings on
a family of weakly asymptotically nonexpansive mappings on  such that
such that  . Assume one of the following assumptions is satisfied:
. Assume one of the following assumptions is satisfied:
(a) satisfies the
satisfies the  -fpp;
-fpp;
(b) is a nonexpansive retract of
is a nonexpansive retract of  .
.
Then for each  , there exists a nonexpansive retraction
, there exists a nonexpansive retraction  from
from  onto
onto  , the common fixed points of
, the common fixed points of  , such that
, such that  , and every closed convex
, and every closed convex  -invariant subset of
-invariant subset of  is also
is also  -invariant.
-invariant.
Proof.
Consider  with the product topology induced by the weak topology on
with the product topology induced by the weak topology on  . Now, consider an
. Now, consider an  and define
and define

By applying an argument similar to that in the proof of [9, Theorem  ], it follows that
], it follows that  is compact (the topology on
is compact (the topology on  is that of weak pointwise convergence) and there is a minimal element
is that of weak pointwise convergence) and there is a minimal element  in the following sense:
in the following sense:

First, we assume the case (a). We shall prove that  for all
for all  . For a given
. For a given  , consider the set
, consider the set  Then
Then  is a nonempty weakly compact convex subset of
is a nonempty weakly compact convex subset of  , because
, because  is convex and compact. We will show that for all
is convex and compact. We will show that for all  ,
,  satisfies property
satisfies property  with respect to
with respect to  . Fix
. Fix  and take
and take  and
and  such as
such as , for some
, for some  . There exists
. There exists  such that
such that  . Consider a subnet
. Consider a subnet  of
of  such that
such that  exists for every
exists for every  . Now, taking
. Now, taking  , we have
, we have  . Since
. Since  is nonexpansive,
is nonexpansive,  , and
, and  , it follows that
, it follows that  and then
and then  . Thus
. Thus  satisfies the property
satisfies the property  with respect to
with respect to  . Since,
. Since,  satisfies the
satisfies the  -fpp (by (a)), it follows that
-fpp (by (a)), it follows that  . So, there exists
. So, there exists  with
with  . Let
. Let  . Then
. Then  , and by using the minimality of
, and by using the minimality of  , we have
, we have

So, we get  . Since this is so for each
. Since this is so for each  and
and  belongs to
belongs to  , it follows that
, it follows that  and
and  .
.
Now, we assume the case (b). From (b), there is a nonexpansive retraction  from
from  onto
onto  . Put
. Put  . Since
. Since  , we can replace
, we can replace  by
by  in the above assertions to obtain a minimal element
in the above assertions to obtain a minimal element  in the sense (*), where
in the sense (*), where  ia defined here as
ia defined here as

We note that  , (
, ( ). Since
). Since  , every closed convex
, every closed convex  -invariant subset of
-invariant subset of  is also
is also  -invariant and consequently
-invariant and consequently  -invariant, (
-invariant, ( ). So it is easy to see that
). So it is easy to see that  , (
, ( ). Therefore, for every
). Therefore, for every  , the set
, the set  is an
is an  -invariant subset of
-invariant subset of  . So, considering the fact that
. So, considering the fact that  , we obtain
, we obtain  . Now, we can repeat the argument used in the last paragraph to get the desired result.
. Now, we can repeat the argument used in the last paragraph to get the desired result.
A nonexpansive retraction satisfying the thesis of Theorem 2.1 is usually called an ergodic retraction (see e.g., [10, 11]).
Combining Theorem 1.5 [9, Theorem  ] and Theorem 2.1(a), we get the following improvement of Theorem 1.5.
] and Theorem 2.1(a), we get the following improvement of Theorem 1.5.
Corollary 2.2.
Let  be a Banach space and
be a Banach space and  a nonempty weakly compact convex subset of
a nonempty weakly compact convex subset of  . Assume that every asymptotically nonexpansive self-mapping of
. Assume that every asymptotically nonexpansive self-mapping of  satisfies
satisfies  -fpp. Then for any commuting family
-fpp. Then for any commuting family  of asymptotically nonexpansive self-mappings of
of asymptotically nonexpansive self-mappings of  and for each
and for each  , there exists a nonexpansive retraction
, there exists a nonexpansive retraction  from
from  onto
onto  , such that
, such that  , and every closed convex
, and every closed convex  -invariant subset of
-invariant subset of  is also
is also  -invariant.
-invariant.
3. Ergodic Retractions for a Semigroup of Asymptotically Nonexpansive Type
Assume that  is a semigroup and
is a semigroup and  is the space of all bounded real-valued functions defined on
is the space of all bounded real-valued functions defined on  with supremum norm. For
with supremum norm. For  and
and  , we define elements
, we define elements  and
and  in
in  by
by  and
and  for each
for each  , respectively. An element
, respectively. An element  of
of  is said to be a mean on
is said to be a mean on  if
if  . We often write
. We often write  instead of
instead of  for
for  and
and  . A mean
. A mean  is said to be invariant if
is said to be invariant if  for each
for each  and
and  .
.  is said to be amenable if there is an invariant mean on
is said to be amenable if there is an invariant mean on  . As is well known,
. As is well known,  is amenable when it is a commutative semigroup [12].
is amenable when it is a commutative semigroup [12].
The following result which we need is well known (see [13]).
Lemma 3.1.
Let  be a function of a semigroup
be a function of a semigroup  into
into  such that the weak closure of
such that the weak closure of  is weakly compact. Then, for any
is weakly compact. Then, for any  , there exists a unique element
, there exists a unique element  in
in  such that
such that  for all
for all  . Moreover, if
. Moreover, if  is a mean, then
is a mean, then 
We can write  by
by  . As a direct consequence of Lemma 3.1, we have the following lemma.
. As a direct consequence of Lemma 3.1, we have the following lemma.
Lemma 3.2.
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  ,
,  a semigroup of weakly asymptotically nonexpansive mappings on
a semigroup of weakly asymptotically nonexpansive mappings on  such that weak closure of
such that weak closure of  is weakly compact for each
is weakly compact for each  , and
, and  a mean on
a mean on  .
.
If we write  instead of
instead of  , then the following hold.
, then the following hold.
(i) for each
for each  .
.
(ii) for each
for each  .
.
(iii)If  is invariant, then
is invariant, then  for each
for each  and
and  is a nonexpansive mapping from
is a nonexpansive mapping from  into itself.
into itself.
Proof.
We only need to prove that  is nonexpansive: consider
is nonexpansive: consider  and
and  . Then for each
. Then for each  , we have
, we have

Therefore,  , for every
, for every  . Consequently, we get
. Consequently, we get

The following is our main result which is an improvement of Theorem 1.4 [4, Theorem  ].
].
Theorem 3.3.
Suppose  is a Banach space with uniform normal structure;
is a Banach space with uniform normal structure;  is a nonempty bounded closed and convex subset of
is a nonempty bounded closed and convex subset of  ;
;  is a semigroup of asymptotically nonexpansive type mappings on
is a semigroup of asymptotically nonexpansive type mappings on  such that
such that  is continuous on
is continuous on  for each
for each  . Then there exists a nonexpansive retraction
. Then there exists a nonexpansive retraction  from
from  onto
onto  , such that
, such that  for each
for each  , and every closed convex
, and every closed convex  -invariant subset of
-invariant subset of  is also
is also  -invariant.
-invariant.
Proof.
Consider  with the product topology induced by the weak topology on
with the product topology induced by the weak topology on  . Now, define
. Now, define

We note that  , because the mapping
, because the mapping  in Lemma 3.2 belongs to
in Lemma 3.2 belongs to  . By applying an argument similar to that in the proof of [9, Theorem
. By applying an argument similar to that in the proof of [9, Theorem  ] (see also the proof of [7, Lemma
] (see also the proof of [7, Lemma  ]), it follows that
]), it follows that  is compact and there is a minimal element
is compact and there is a minimal element  in the following sense:
in the following sense:

We will prove that  for all
for all  . For a given
. For a given  , consider the set
, consider the set  Then
Then  is a nonempty weakly compact convex subset of
is a nonempty weakly compact convex subset of  , because
, because  is convex and compact. Take
is convex and compact. Take  and
and  such as
such as , for some
, for some . There exists
. There exists  , such that
, such that  . Consider a subnet
. Consider a subnet  of
of  such that
such that  exists for every
exists for every  . Now, taking
. Now, taking  , we have
, we have  . Since
. Since  is nonexpansive,
is nonexpansive,  and
and  for every
for every  , it follows that
, it follows that  and then
and then  . Thus
. Thus  satisfies the property
satisfies the property  with respect to the semigroup
with respect to the semigroup  . Now, from Theorem 1.4, it follows that
. Now, from Theorem 1.4, it follows that  . From this and the argument used in the proof of Theorem 2.1, we obtain
. From this and the argument used in the proof of Theorem 2.1, we obtain  . Since this holds for each
. Since this holds for each  ,
,  .
.
References
Kirk WA: A fixed point theorem for mappings which do not increase distances. Proceedings of the American Mathematical Society 1965, 72: 1004–1006.
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3
Kirk WA: Fixed point theorems for non-lipschitzian mappings of asymptotically nonexpansive type. Israel Journal of Mathematics 1974, 17: 339–346. 10.1007/BF02757136
Li G, Sims B: Fixed point theorems for mappings of asymptotically nonexpansive type. Nonlinear Analysis: Theory, Methods & Applications 2002, 50: 1085–1091. 10.1016/S0362-546X(01)00744-1
Bruck RE: Properties of fixed-point sets of nonexpansive mappings. Transactions of the American Mathematical Society 1973, 179: 251–262.
Bruck RE: A common fixed point theorem for a commuting family of nonexpansive mappings. Pacific Journal of Mathematics 1974, 53: 59–71.
Saeidi S: Ergodic retractions for amenable semigroups in Banach spaces with normal structure. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):2558–2563. 10.1016/j.na.2009.01.091
Saeidi S: The retractions onto the common fixed points of some families and semigroups of mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(3–4):1171–1179. 10.1016/j.na.2008.11.049
Benavides Td, Ramírez PL: Structure of the fixed point set and common fixed points of asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 2001,129(12):3549–3557. 10.1090/S0002-9939-01-06141-X
Kirk WA, Sims B: Handbook of Metric Fixed Point Theory. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:xiv+703.
Lau AT, Shioji N, Takahashi W: Existence of nonexpansive retractions for amenable semigroups of nonexpansive mappings and nonlinear ergodic theorems in Banach spaces. Journal of Functional Analysis 1999,161(1):62–75. 10.1006/jfan.1998.3352
Day MM: Amenable Semigroups. Illinois Journal of Mathematics 1957, 1: 509–544.
Takahashi W: A nonlinear ergodic theorem for an amenable semigroup of nonexpansive mappings in a Hilbert space. Proceedings of the American Mathematical Society 1981,81(2):253–256. 10.1090/S0002-9939-1981-0593468-X
Acknowledgments
The author would like to thank the referee for useful comments and for pointing out an oversight regarding an earlier draft of this paper. This paper is dedicated to Professor William Art Kirk. This research was in part supported by a Grant from IPM (no. 88470021).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saeidi, S. Ergodic Retractions for Families of Asymptotically Nonexpansive Mappings. Fixed Point Theory Appl 2010, 281362 (2010). https://doi.org/10.1155/2010/281362
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/281362
 is said to satisfy the
is said to satisfy the 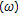 -fixed point property (
-fixed point property ( -fpp) if
-fpp) if  has a fixed point in every nonempty closed convex subset
has a fixed point in every nonempty closed convex subset  of
of  which satisfies
which satisfies 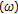 with respect to
with respect to  .
.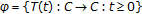 is said to satisfy the
is said to satisfy the  -fpp if
-fpp if 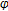 has a common fixed point in every nonempty closed convex subset
has a common fixed point in every nonempty closed convex subset  of
of  which satisfies
which satisfies 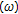 with respect to the semigroup
with respect to the semigroup 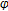 .
.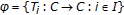 is said to satisfy the
is said to satisfy the 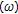 -fpp if
-fpp if 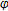 has a common fixed point in every nonempty closed convex subset
has a common fixed point in every nonempty closed convex subset  of
of  which satisfies
which satisfies 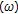 with respect to each
with respect to each  .
.