- Research Article
- Open access
- Published:
On Equivalence of Some Iterations Convergence for Quasi-Contraction Maps in Convex Metric Spaces
Fixed Point Theory and Applications volume 2010, Article number: 252871 (2010)
Abstract
We show the equivalence of the convergence of Picard and Krasnoselskij, Mann, and Ishikawa iterations for the quasi-contraction mappings in convex metric spaces.
1. Introduction
Let  be a complete metric space and
be a complete metric space and  . Denote
. Denote  . A continuous mapping W
. A continuous mapping W is said to be a convex structure on
is said to be a convex structure on  [1] if for all
[1] if for all  with
with  such that
such that


If  satisfies the conditions of convex structure, then
satisfies the conditions of convex structure, then  is called convex metric space that is denoted as
is called convex metric space that is denoted as  .
.
In the following part, we will consider a few iteration sequences in convex metric space  . Suppose that
. Suppose that  is a self-map of
is a self-map of  .
.
Picard iteration is as follows:

Krasnoselskij iteration is as follows:

where  .
.
Mann iteration is as follows:

where  .
.
Ishikawa iteration is as follows:

where  for all
for all  .
.
A mapping  is called contractive if there exists
is called contractive if there exists  such that
such that

for all  .
.
The map  is called Kannan mapping [2] if there exists
is called Kannan mapping [2] if there exists  such that
such that

for all  .
.
A similar definition of mapping is due to the work Chatterjea [3] (that is called Chatterjea mapping), if there exists  such that
such that

for all  .
.
Combining above three definitions, Zamfirescu [4] showed the following result.
Theorem 1.1.
Let  be a complete metric space and
be a complete metric space and  a mapping for which there exist the real numbers
a mapping for which there exist the real numbers  and
and  satisfying
satisfying  such that, for any pair
such that, for any pair  , at least one of the following conditions holds:
, at least one of the following conditions holds:
(z1) 
(z2) 
(z3) 
Then  has a unique fixed point, and the Picard iteration converges to fixed point. This class mapping is called Zamfirescu mapping.
has a unique fixed point, and the Picard iteration converges to fixed point. This class mapping is called Zamfirescu mapping.
In 1974,  irić [5] introduced one of the most general contraction mappings and obtained that the unique fixed point can be approximated by Picard iteration. This mapping is called quasi-contractive if there exists
irić [5] introduced one of the most general contraction mappings and obtained that the unique fixed point can be approximated by Picard iteration. This mapping is called quasi-contractive if there exists  such that
such that

for any  .
.
Clearly, every quasi-contraction mapping is the most general of above mappings.
Later on, in 1992, Xu [6] proved that Ishikawa iteration can also be used to approximate the fixed points of quasi-contraction mappings in real Banach spaces.
Theorem 1.2.
Let  be any nonempty closed convex subset of a Banach space
be any nonempty closed convex subset of a Banach space  and
and  a quasi-contraction mapping. Suppose that
a quasi-contraction mapping. Suppose that  for all
for all  and
and  . Then the Ishikawa iteration sequence
. Then the Ishikawa iteration sequence  defined by (1)–(3) converges strongly to the unique fixed point
defined by (1)–(3) converges strongly to the unique fixed point  of
of  .
.
In this paper, we will show the equivalence of the convergence of Picard and Krasnoselskij, Mann, and Ishikawa iterations for the quasi-contraction mappings in convex metric spaces.
Lemma 1.3.
Let  be a nonnegative sequence which satisfies the following inequality
be a nonnegative sequence which satisfies the following inequality

where  , and
, and  as
as  . Then
. Then  as
as  (see [7]).
(see [7]).
2. Results for Quasi-Contraction Mappings
Theorem 2.1.
Let  be a convex metric space,
be a convex metric space,  a quasi-contraction mapping with
a quasi-contraction mapping with  . Suppose that
. Suppose that  are defined by the iterative processes (1.3) and (1.4), respectively. Then, the following two assertions are equivalent:
are defined by the iterative processes (1.3) and (1.4), respectively. Then, the following two assertions are equivalent:
(i)Picard iteration (1.3) converges strongly to the unique fixed point  ;
;
(ii)Krasnoselskij iteration (1.4) converges strongly to the unique fixed point  .
.
Proof.
First, we show  , that is,
, that is,  as
as  as
as  .
.
From (1.3), (1.4), and (1.1), we can get

Next, we consider  . Using (1.10) with
. Using (1.10) with  , to obtain
, to obtain

Set

Then  is bounded. Without loss of generality, we let
is bounded. Without loss of generality, we let  for each
for each  . Indeed, we will show this conclusion from the some following cases.
. Indeed, we will show this conclusion from the some following cases.
Case 1  .
.
Let  for some
for some  . Then, from (1.10) and the above
. Then, from (1.10) and the above  , we have
, we have

and it leads to a contradiction. Thus,  . Similarity to
. Similarity to  or
or  is also impossible.
is also impossible.
Case 2  .
.
Let  for some
for some  .
.
(i)If  , then
, then  .
.
(ii)If  , then, from (1.4) and (1.1)
, then, from (1.4) and (1.1)

that is,  . By induction on
. By induction on  , we can obtain
, we can obtain  .
.
-
(iii)
If
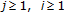 , from (1.4) and (1.1)
, from (1.4) and (1.1) 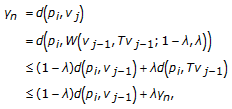 (2.6)
(2.6)
it implies that  . By induction on
. By induction on  , we can get
, we can get  .
.
Case 3  .
.
Let  for some
for some  . Without loss of generality, we set
. Without loss of generality, we set  . Then, from (1.4), (1.1)
. Then, from (1.4), (1.1)

it implies that  , and by induction on
, and by induction on  , we may get
, we may get  , which is a contradiction.
, which is a contradiction.
Case 4  .
.
Let  for some
for some  .
.
(i)If  , then
, then  .
.
(ii)If  , from (1.4), (1.1), then
, from (1.4), (1.1), then

it implies that  and by induction on
and by induction on  , then
, then  .
.
Case 5  .
.
Let  for some
for some  .
.
(i)If  , then
, then  .
.
(ii)If  , then, from (1.3) and (1.10)
, then, from (1.3) and (1.10)

this is a contradiction.
Case 6  .
.
let  for some
for some  .
.
(i)If  , then
, then  .
.
(ii)If  , then, from (1.4) and (1.10)
, then, from (1.4) and (1.10)

it implies that  .
.
Case 7  .
.
Let  for some
for some  .
.
(i)If  , then
, then  .
.
(ii)If  , then, from (1.3), (1.10)
, then, from (1.3), (1.10)

it is a contradiction.
Case 8  .
.
let  for some
for some  .
.
(i)If  , then
, then  .
.
(ii)If  , then, from (1.3) and (1.10)
, then, from (1.3) and (1.10)

which is a contradiction.
Set

where  .
.
In view of the above cases, then  , and we obtain that
, and we obtain that  is bounded.
is bounded.
Indeed, suppose that  for some
for some  . Then,
. Then,

which implies that  . Similarly, if
. Similarly, if  or
or  , we also obtain
, we also obtain  .
.
On the other hand, suppose that  for some
for some  . Then,
. Then,

which implies that  . Similarly, if
. Similarly, if  or
or  , we also obtain
, we also obtain  . Therefore, from the above results, we obtain that
. Therefore, from the above results, we obtain that  , that is,
, that is,  is bounded.
is bounded.
For each  , define
, define

Then, using the same proof above, it can be shown that

If  , and using (1.1) and (1.4), then
, and using (1.1) and (1.4), then

as  . Since
. Since  , hence
, hence  as
as  . Similarly, if
. Similarly, if  or
or  ,
,  , we may obtain the similar results. Therefore, from (2.1), we get
, we may obtain the similar results. Therefore, from (2.1), we get

where 
In (2.19), set  . Then (2.19) is as follows:
. Then (2.19) is as follows:

By Lemma 1.3, we have  as
as  . From the inequality
. From the inequality  , we have
, we have  .
.
Conversely, we will prove that  . If
. If  , then
, then  is Picard iteration.
is Picard iteration.
Theorem 2.2.
Let  be as in Theorem 2.1. Suppose that
be as in Theorem 2.1. Suppose that  are defined by the iterative processes (1.5) and (1.6), respectively, and
are defined by the iterative processes (1.5) and (1.6), respectively, and  are real sequences in
are real sequences in  such that
such that  . Then, the following two assertions are equivalent:
. Then, the following two assertions are equivalent:
(i)Mann iteration (1.5) converges strongly to the unique fixed point  ;
;
(ii)Ishikawa iteration (1.6) converges strongly to the unique fixed point  .
.
Proof.
If the Ishikawa iteration (1.6) converges strongly to  , then setting
, then setting  , in (1.6), we can get the convergence of Mann iteration (1.5). Conversely, we will show that
, in (1.6), we can get the convergence of Mann iteration (1.5). Conversely, we will show that  . Letting
. Letting  , we want to prove
, we want to prove  .
.
From (1.5) and (1.6),

Using (1.10) with  , to obtain
, to obtain

set

Applying the similar proof methods of Theorem 2.1, we obtain that  is also bounded. The other proof is the same as that of Theorem 2.1 and is here omitted.
is also bounded. The other proof is the same as that of Theorem 2.1 and is here omitted.
References
Takahashi W: A convexity in metric space and nonexpansive mappings. I. Kōdai Mathematical Seminar Reports 1970, 22: 142–149. 10.2996/kmj/1138846111
Kannan R: Some results on fixed points. Bulletin of the Calcutta Mathematical Society 1968, 60: 71–76.
Chatterjea SK: Fixed-point theorems. Comptes Rendus de l'Académie Bulgare des Sciences 1972, 25: 727–730.
Zamfirescu T: Fix point theorems in metric spaces. Archiv der Mathematik 1972, 23: 292–298. 10.1007/BF01304884
Ćirić LB: A generalization of Banach's contraction principle. Proceedings of the American Mathematical Society 1974, 45: 267–273.
Xu HK: A note on the Ishikawa iteration scheme. Journal of Mathematical Analysis and Applications 1992,167(2):582–587. 10.1016/0022-247X(92)90225-3
Weng X: Fixed point iteration for local strictly pseudo-contractive mapping. Proceedings of the American Mathematical Society 1991,113(3):727–731. 10.1090/S0002-9939-1991-1086345-8
Acknowledgments
The authors are extremely grateful to Professor B. E. Rhoades of Indiana University for providing useful information and many help. They also thank the referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xue, Z., Lv, G. & Rhoades, B. On Equivalence of Some Iterations Convergence for Quasi-Contraction Maps in Convex Metric Spaces. Fixed Point Theory Appl 2010, 252871 (2010). https://doi.org/10.1155/2010/252871
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/252871
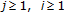 , from (1.4) and (1.1)
, from (1.4) and (1.1)