- Research Article
- Open access
- Published:
Some Fixed Point Theorems of Integral Type Contraction in Cone Metric Spaces
Fixed Point Theory and Applications volume 2010, Article number: 189684 (2010)
Abstract
We define a new concept of integral with respect to a cone. Moreover, certain fixed point theorems in those spaces are proved. Finally, an extension of Meir-Keeler fixed point in cone metric space is proved.
1. Introduction
In 2007, Huang and Zhang in [1] introduced cone metric space by substituting an ordered Banach space for the real numbers and proved some fixed point theorems in this space. Many authors study this subject and many fixed point theorems are proved; see [2–5]. In this paper, the concept of integral in this space is introduced and a fixed point theorem is proved. In order to do this, we recall some definitions, examples, and lemmas from [1, 4] as follows.
Let  be a real Banach space. A subset
be a real Banach space. A subset  of
of  is called a cone if and only if the following hold:
is called a cone if and only if the following hold:
(i) is closed, nonempty, and
is closed, nonempty, and  ,
,
(ii) ,
,  , and
, and  imply that
imply that 
(iii) and
and  imply that
imply that 
Given a cone  we define a partial ordering
we define a partial ordering  with respect to
with respect to  by
by  if and only if
if and only if  We will write
We will write  to indicate that
to indicate that  but
but  , while
, while  will stand for
will stand for  int
int where int
where int  denotes the interior of
denotes the interior of  The cone
The cone  is called normal if there is a number
is called normal if there is a number  such that
such that  implies
implies  for all
for all  The least positive number satisfying above is called the normal constant [1].
The least positive number satisfying above is called the normal constant [1].
The cone  is called regular if every increasing sequence which is bounded from above is convergent. That is, if
is called regular if every increasing sequence which is bounded from above is convergent. That is, if  is a sequence such that
is a sequence such that  for some
for some  , then there is
, then there is  such that
such that  . Equivalently, the cone
. Equivalently, the cone  is regular if and only if every decreasing sequence which is bounded from below is convergent [1]. Also every regular cone is normal [4]. In addition, there are some nonnormal cones.
is regular if and only if every decreasing sequence which is bounded from below is convergent [1]. Also every regular cone is normal [4]. In addition, there are some nonnormal cones.
Example 1.1.
Suppose  with the norm
with the norm  and consider the cone
and consider the cone  :
:  . For all
. For all  , set
, set  and
and  Then
Then 
 and
and  Since
Since 
 is not normal constant of
is not normal constant of  Therefore,
Therefore,  is non-normal cone.
is non-normal cone.
From now on, we suppose that  is a real Banach space,
is a real Banach space,  is a cone in
is a cone in  with
with  and
and  is partial ordering with respect to
is partial ordering with respect to  . Let
. Let  be a nonempty set. As it has been defined in [1], a function
be a nonempty set. As it has been defined in [1], a function  is called a cone metric on
is called a cone metric on  if it satisfies the following conditions:
if it satisfies the following conditions:
(i) for all
for all  and
and  if and only if
if and only if 
(ii) , for all
, for all 
(iii) , for all
, for all 
Then  is called a cone metric space.
is called a cone metric space.
Example 1.2.
Suppose 

 is a metric space and
is a metric space and  is defined by
is defined by  Then
Then  is a cone metric space and the normal constant of
is a cone metric space and the normal constant of  is equal to
is equal to 
Definition 1.3.
Let  be a cone metric space. Let
be a cone metric space. Let  be a sequence in
be a sequence in  and
and  If for any
If for any  with
with  there is
there is  such that for all
such that for all  ,
,  then
then  is said to be convergent to
is said to be convergent to  and
and  is the limit of
is the limit of  . We denote this by
. We denote this by

Definition 1.4.
Let  be a cone metric space and
be a cone metric space and  be a sequence in
be a sequence in  If for any
If for any  with
with  , there is
, there is  such that for all
such that for all 
 then
then  is called a Cauchy sequence in
is called a Cauchy sequence in 
Definition 1.5.
Let  be a cone metric space, if every Cauchy sequence is convergent in
be a cone metric space, if every Cauchy sequence is convergent in  then
then  is called a complete cone metric space.
is called a complete cone metric space.
Definition 1.6.
Let  be a cone metric space. Let
be a cone metric space. Let  be a self-map on
be a self-map on  If for all sequence
If for all sequence  in
in 

then  is called continuous on
is called continuous on 
The following lemmas are useful for us to prove the main result.
Lemma 1.7.
Let  be a cone metric space and
be a cone metric space and  a normal cone with normal constant
a normal cone with normal constant  Let
Let  be a sequence in
be a sequence in  Then
Then  converges to
converges to  if and only if
if and only if

Lemma 1.8.
Let  be a cone metric space and
be a cone metric space and  a normal cone with normal constant
a normal cone with normal constant  Let
Let  be a sequence in
be a sequence in  . Then
. Then  is a Cauchy sequence if and only if
is a Cauchy sequence if and only if

Lemma 1.9.
Let  be a cone metric space and
be a cone metric space and  a sequence in
a sequence in  If
If  is convergent, then it is a Cauchy sequence.
is convergent, then it is a Cauchy sequence.
Lemma 1.10.
Let  be a cone metric space and
be a cone metric space and  be a normal cone with normal constant
be a normal cone with normal constant  . Let
. Let  and
and  be two sequences in
be two sequences in  and
and 
 . Then
. Then

The following example is a cone metric space.
Example 1.11.
Let 
 and
and  Suppose that
Suppose that  is defined by
is defined by  where
where  is a constant. Then
is a constant. Then  is a cone metric space.
is a cone metric space.
Theorem 1.12.
Let  be a complete cone metric space and
be a complete cone metric space and  a normal cone with normal constant
a normal cone with normal constant  Suppose the mapping
Suppose the mapping  satisfies the contractive condition
satisfies the contractive condition

for all  where
where  is a constant. Then
is a constant. Then  has a unique fixed point
has a unique fixed point  Also, for all
Also, for all  the sequence
the sequence  converges to
converges to 
2. Certain Integral Type Contraction Mapping in Cone Metric Space
In 2002, Branciari in [6] introduced a general contractive condition of integral type as follows.
Theorem 2.1.
Let  be a complete metric space,
be a complete metric space,  , and
, and  is a mapping such that for all
is a mapping such that for all 

where  is nonnegative and Lebesgue-integrable mapping which is summable (i.e., with finite integral) on each compact subset of
is nonnegative and Lebesgue-integrable mapping which is summable (i.e., with finite integral) on each compact subset of  such that for each
such that for each  ,
,  , then
, then  has a unique fixed point
has a unique fixed point  , such that for each
, such that for each 

In this section we define a new concept of integral with respect to a cone and introduce the Branciari's result in cone metric spaces.
Definition 2.2.
Suppose that  is a normal cone in
is a normal cone in  . Let
. Let  and
and  . We define
. We define

Definition 2.3.
The set  is called a partition for
is called a partition for  if and only if the sets
if and only if the sets  are pairwise disjoint and
are pairwise disjoint and 
Definition 2.4.
For each partition  of
of  and each increasing function
and each increasing function  we define cone lower summation and cone upper summation as
we define cone lower summation and cone upper summation as

respectively.
Definition 2.5.
Suppose that  is a normal cone in
is a normal cone in  .
.  is called an integrable function on
is called an integrable function on  with respect to cone
with respect to cone  or to simplicity, Cone integrable function, if and only if for all partition
or to simplicity, Cone integrable function, if and only if for all partition  of
of 

where  must be unique.
must be unique.
We show the common value  by
by

We denote the set of all cone integrable function  by
by  .
.
Lemma 2.6.
-
(1)
If
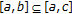 , then
, then  for
for 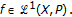 (2)
(2) 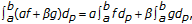 for
for 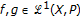 and
and 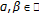 .
.
Proof.
-
(1)
Suppose that
 and
and  are partitions for
are partitions for 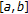 and
and 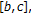 respectively. That is,
respectively. That is,  (2.6)
(2.6)
Let 
 is a partition for
is a partition for  Therefore one can write
Therefore one can write

So

-
(2)
Suppose
 is an partition for
is an partition for  , that is
, that is 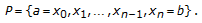 (2.9)
(2.9)
Then

Thus

Definition 2.7.
The function  is called subadditive cone integrable function if and only if for all
is called subadditive cone integrable function if and only if for all 

Example 2.8.
Let  ,
,  ,
,  and
and  for all
for all  Then for all
Then for all 

Since  then
then  . Therefore
. Therefore

This shows that  is an example of subadditive cone integrable function.
is an example of subadditive cone integrable function.
Theorem 2.9.
Let  be a complete cone metric space and
be a complete cone metric space and  a normal cone. Suppose that
a normal cone. Suppose that  is a nonvanishing map and a subadditive cone integrable on each
is a nonvanishing map and a subadditive cone integrable on each  such that for each
such that for each  ,
,  . If
. If  is a map such that, for all
is a map such that, for all 

for some  then
then  has a unique fixed point in
has a unique fixed point in 
Proof.
Let  Choose
Choose  We have
We have

Since  thus
thus

If  then
then  and this is a contradiction, so
and this is a contradiction, so

We now show that  is a Cauchy sequence. Due to this, we show that
is a Cauchy sequence. Due to this, we show that

By triangle inequality

and by sub-additivity of  we get
we get

Thus

This means that  is a Cauchy sequence and since
is a Cauchy sequence and since  is a complete cone metric space, thus
is a complete cone metric space, thus  is convergent to
is convergent to  Finally, since
Finally, since

thus  This means that
This means that  If
If  are two distinct fixed points of
are two distinct fixed points of  then
then

which is a contradiction. Thus  has a unique fixed point
has a unique fixed point 
Lemma 2.10.
Let 
 and
and  Suppose that
Suppose that  is defined by
is defined by  where
where  is a constant. Suppose that
is a constant. Suppose that  is defined by
is defined by  where
where  are two Riemann-integrable functions. Then
are two Riemann-integrable functions. Then

Proof.
Let  be a partition of set
be a partition of set  such that
such that  and
and  , then (by Definitions 2.4 and 2.5)
, then (by Definitions 2.4 and 2.5)

Thus

Example 2.11.
Let 
 and
and  Suppose
Suppose  for some constant
for some constant  Firstly,
Firstly,  is a complete cone metric space. Secondly, if
is a complete cone metric space. Secondly, if  and
and  are defined by
are defined by

respectively, then

In order to obtain inequality (2.29), set  and
and  where
where  Hence
Hence

Suppose  for all
for all  and
and  . Thus
. Thus  . By Lemma 2.10
. By Lemma 2.10

Since  thus
thus

It means that

On the other side, Branciari in [6] shows that

for all  . Therefore
. Therefore

Thus inequalities (2.33) and (2.35) imply that

or in other words

Thus by Theorem 2.9,  has a fixed point. But, on the other hand,
has a fixed point. But, on the other hand,

and this means that  does not satisfy in Theorem 1.12.
does not satisfy in Theorem 1.12.
3. Extension of Meir-Keeler Contraction in Cone Metric Space
In 2006, Suzuki in [7] proved that the integral type contraction (see [6]) is a special case of Meir-Keeler contraction (see [8]). Haghi and Rezapour in [5] extended Meir-Keeler contraction in cone metric space as follows.
Theorem 3.1 (see[5]).
Let  be a complete regular cone metric space and
be a complete regular cone metric space and  has the property (KMC) on
has the property (KMC) on  that is, for all
that is, for all  , there exists
, there exists  such that
such that

for all  . Then
. Then  has a unique fixed point.
has a unique fixed point.
An extension of Theorem 3.1 is as follows.
Theorem 3.2.
Let  be a complete regular cone metric space and
be a complete regular cone metric space and  a mapping on
a mapping on  . Suppose that there exists a function
. Suppose that there exists a function  from
from  into itself satisfying the following:
into itself satisfying the following:
 and
and  for all
for all  ,
,
 is nondecreasing and continuous function. Moreover, its inverse is continuous,
is nondecreasing and continuous function. Moreover, its inverse is continuous,
for all  there exists
there exists  such that for all
such that for all 

for all 

Then  has a unique fixed point.
has a unique fixed point.
Proof.
First, note that  for all
for all  with
with  Since
Since  exists, thus
exists, thus  for all
for all  with
with  Now Let
Now Let  Set
Set  for all
for all  If, there is a natural
If, there is a natural  such that
such that  then
then  and so
and so  has a fixed point. If
has a fixed point. If  for all
for all  then
then  Hence, according to regularity of
Hence, according to regularity of  there exists
there exists  such that
such that  We claim
We claim  If
If  then according to
then according to  there is
there is  such that
such that  for all
for all  with
with  Choose
Choose  such that
such that  and take the natural number
and take the natural number  such that
such that  for all
for all  We obtain
We obtain

Thus

So,  Since
Since  has the property
has the property 
 for all
for all  . This is a contradiction because
. This is a contradiction because  for all
for all  Thus
Thus

Now, we show that  is a Cauchy sequence. If this is not, then there is a
is a Cauchy sequence. If this is not, then there is a  such that for all natural number
such that for all natural number  there are
there are  so that the relation
so that the relation  does not hold. Since
does not hold. Since  has continuous inverse thus there exists
has continuous inverse thus there exists  such that for all natural number
such that for all natural number  there are
there are  so that the relation
so that the relation  does not hold. For each
does not hold. For each  there exists
there exists  such that
such that  for all
for all  with
with  Choose a natural number
Choose a natural number  such that
such that  for all
for all  Also, take
Also, take  so that the relation
so that the relation  does not hold. Then
does not hold. Then  yields
yields

Hence,  Similarly,
Similarly,  Thus
Thus

which is a contradiction. Therefore  is a Cauchy sequence. Since
is a Cauchy sequence. Since  is a complete cone metric space, there is
is a complete cone metric space, there is  such that
such that  . Since
. Since  , for all
, for all  with
with  , thus for each
, thus for each  , there is a natural number
, there is a natural number  such that for all
such that for all  ,
,  Since
Since  thus
thus  for all
for all  . It means that
. It means that  In the other side,
In the other side,  and the limit point is unique in cone metric spaces. Thus
and the limit point is unique in cone metric spaces. Thus  has at least one fixed point. Now, if
has at least one fixed point. Now, if  are two distinct fixed points for
are two distinct fixed points for  then
then

which is a contradiction. Therefore  has a unique fixed point.
has a unique fixed point.
Remark 3.3.
 Set
Set  , then Theorem 3.1 is a direct result of Theorem 3.2.
, then Theorem 3.1 is a direct result of Theorem 3.2.
 Let
Let  be a nonvanishing map and a subadditive cone integrable on each
be a nonvanishing map and a subadditive cone integrable on each  such that for each
such that for each  ,
,  If
If  then
then  satisfies all conditions of Theorem 3.2. In other words, Theorem 2.9 is a direct result of Theorem 3.2.
satisfies all conditions of Theorem 3.2. In other words, Theorem 2.9 is a direct result of Theorem 3.2.
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. Journal of Mathematical Analysis and Applications 2008,341(1):416–420. 10.1016/j.jmaa.2007.09.070
Ilić D, Rakočević V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Rezapour Sh, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Haghi RH, Rezapour Sh: Fixed points of multifunctions on regular cone metric spaces. Expositiones Mathematicae 2010,28(1):71–77. 10.1016/j.exmath.2009.04.001
Branciari A: A fixed point theorem for mappings satisfying a general contractive condition of integral type. International Journal of Mathematics and Mathematical Sciences 2002,29(9):531–536. 10.1155/S0161171202007524
Suzuki T: Meir-Keeler contractions of integral type are still Meir-Keeler contractions. International Journal of Mathematics and Mathematical Sciences 2007, 2007:-6.
Meir A, Keeler E: A theorem on contraction mappings. Journal of Mathematical Analysis and Applications 1969, 28: 326–329. 10.1016/0022-247X(69)90031-6
Acknowledgment
The third author would like to thank the School of Mathematics of the Institute for Research in Fundamental Sciences, Teheran, Iran, for supporting this research (Grant no. 88470119).
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1155/2011/346059.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Khojasteh, F., Goodarzi, Z. & Razani, A. Some Fixed Point Theorems of Integral Type Contraction in Cone Metric Spaces. Fixed Point Theory Appl 2010, 189684 (2010). https://doi.org/10.1155/2010/189684
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/189684
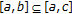 , then
, then  for
for 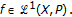 (2)
(2) 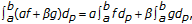 for
for 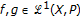 and
and 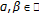 .
. and
and  are partitions for
are partitions for 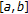 and
and 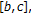 respectively. That is,
respectively. That is, 
 is an partition for
is an partition for  , that is
, that is