- Research Article
- Open access
- Published:
Fixed Points of Single- and Set-Valued Mappings in Uniformly Convex Metric Spaces with No Metric Convexity
Fixed Point Theory and Applications volume 2010, Article number: 169837 (2009)
Abstract
We study the existence of fixed points and convergence of iterates for asymptotic pointwise contractions in uniformly convex metric spaces. We also study the existence of fixed points for set-valued nonexpansive mappings in the same class of spaces. Our results do not assume convexity of the metric which makes a big difference when studying the existence of fixed points for set-valued mappings.
1. Introduction
This paper is motivated by the recent paper [1]. In [1] the authors study different questions related to fixed points of asymptotic pointwise contractive/nonexpansive mappings in CAT(0) spaces. CAT(0) spaces are studied in [1] as a very significant example within the class of uniformly convex metric spaces (the reader can consult [2] for details on CAT(0) spaces). In our present paper we propose to consider similar questions on uniformly convex metric spaces under the mildest additional conditions we may impose. More precisely, we will work with uniformly convex metric spaces with either a monotone modulus of convexity in the sense first given in [3] or a lower semicontinuous from the right modulus of convexity (see Section 2 for proper definitions). For a recent survey on the existence of fixed points in geodesic spaces, the reader may check [4], for recent achievements on related topics the reader may also check [5].
The notion of asymptotic pointwise contractions was introduced in [6]. Then it was also studied in [7] where, by means of ultrapower techniques, different results about the existence of fixed points and convergence of iterates were proved. In [8] new proofs were presented but this time after applying only elementary techniques. Very recently, in [1], these techniques were applied in CAT(0), where the authors attend to the Bruhat-Tits inequality for CAT(0) spaces in order to obtain such results. In the present paper we show that actually most of those results still hold for general uniformly convex metric spaces under mild conditions on the modulus of convexity. In Section 3 we focus on single-valued mappings and, in particular, on mappings which are asymptotically pointwise contractive/nonexpansive to study the existence of fixed points, convergence of Picard's iterates, and the structure of their sets of fixed points. As a technical result we need to show that bounded sequences in these spaces have a unique asymptotic center which, as a by-product, leads to Kirk's Fixed Point Theorem. In Section 4 we study different problems regarding set-valued mappings in these spaces. The main technical difficulty to achieve similar results to those shown in [1] is that now we cannot count on the existence of fixed points for nonexpansive set-valued mappings for the kind of spaces we deal with. Finding fixed point for set-valued nonexpansive mappings in uniformly convex metric spaces was first studied by Shimizu and Takahashi [9], where the existence of fixed points was guaranteed under stronger conditions on the modulus of convexity and the additional condition of metric convexity of the space. The fact that we do not have that the metric are convex will make the problem more complicated and this will take us to impose new conditions on the modulus of convexity which we will relate with the geometry of the space.
2. Basic Definitions and Results
We introduce next some basic definitions.
Definition 2.1.
Let  be a metric space. A mapping
be a metric space. A mapping  is called a pointwise contraction if there exists a mapping
is called a pointwise contraction if there exists a mapping  such that
such that

for any  .
.
It is proved in [8] (see also [6]) that if  is a weakly compact convex subset of a Banach space and
is a weakly compact convex subset of a Banach space and  is a pointwise contraction, then
is a pointwise contraction, then  has a unique fixed point and the sequence of the iterates of
has a unique fixed point and the sequence of the iterates of  converges to the fixed point for any
converges to the fixed point for any  . As it is pointed out in [1], the uniqueness of fixed points and convergence of iterates for these mappings directly follow if existence is guaranteed.
. As it is pointed out in [1], the uniqueness of fixed points and convergence of iterates for these mappings directly follow if existence is guaranteed.
Definition 2.2.
Let  be a metric space. Let
be a metric space. Let  be a mapping, and let
be a mapping, and let  for each
for each  be such that
be such that

Then
(i) is called an asymptotic pointwise contraction if
is called an asymptotic pointwise contraction if  converges pointwise to
converges pointwise to  ;
;
(ii) is called an asymptotic pointwise nonexpansive mapping if
is called an asymptotic pointwise nonexpansive mapping if  for any
for any  ;
;
(iii) is called a strongly asymptotic pointwise contraction if
is called a strongly asymptotic pointwise contraction if  , with
, with  , for any
, for any  .
.
In this paper we will mainly work with uniformly convex geodesic metric space. Since the definition of uniform convexity requires the existence of midpoints, the word geodesic is redundant and so, for simplicity, we will usually omit it.
Definition 2.3.
A geodesic metric space  is said to be uniformly convex if for any
is said to be uniformly convex if for any  and any
and any  there exists
there exists  such that for all
such that for all  with
with  ,
,  and
and  it is the case that
it is the case that

where  stands for any midpoint of any geodesic segment
stands for any midpoint of any geodesic segment  . A mapping
. A mapping  providing such a
providing such a  for a given
for a given  and
and  is called a modulus of uniform convexity.
is called a modulus of uniform convexity.
Notice that this definition of uniform convex metric spaces is weaker than the one used in [9] in two ways. First, we do not impose that the metric is convex and, second, our modulus of convexity does depend on the two variables  and
and  while it is assumed to depend only on
while it is assumed to depend only on  in [9].
in [9].
Definition 2.4.
Let  be a metric space, then the metric is said to be convex if for any
be a metric space, then the metric is said to be convex if for any  and
and  in
in  , and
, and  a midpoint in between
a midpoint in between  and
and  ,
,

It is easy to see that uniformly convex metric spaces are uniquely geodesic, that is, for each two points there is just one geodesic joining them. Therefore midpoints and geodesic segments  joining two points are unique. In this case there is a natural way to define convexity. A subset
joining two points are unique. In this case there is a natural way to define convexity. A subset  of a (uniquely) geodesic space is said to be convex if
of a (uniquely) geodesic space is said to be convex if  for any
for any  . For more about geodesic spaces the reader may check [2].
. For more about geodesic spaces the reader may check [2].
To obtain our results we will need to impose additional conditions on the modulus of convexity. Following [3, 10] we consider the notion of monotone modulus of convexity as follows.
Definition 2.5.
If a uniformly convex metric space  admits a modulus of convexity
admits a modulus of convexity  such that it decreases with
such that it decreases with  (for each fixed
(for each fixed  ) then we say that
) then we say that  is a monotone modulus of convexity for
is a monotone modulus of convexity for  .
.
In the same way we define a lower semicontinuous from the right modulus of convexity as follows.
Definition 2.6.
If a uniformly convex metric space  admits a modulus of convexity
admits a modulus of convexity  such that it is lower semicontinuous from the right with respect to
such that it is lower semicontinuous from the right with respect to  (for each fixed
(for each fixed  ) then we say
) then we say  is a lower semicontinuous from the right modulus of convexity for
is a lower semicontinuous from the right modulus of convexity for  .
.
Let  be a metric space and
be a metric space and  a family of subsets of
a family of subsets of  . Then, following [1], we say that
. Then, following [1], we say that  defines a convexity structure on
defines a convexity structure on  if it contains the closed balls and is stable by intersection.
if it contains the closed balls and is stable by intersection.
Let  be a metric space and
be a metric space and  a convexity structure on
a convexity structure on  . Given
. Given  , we say that
, we say that  is
is  -convex if
-convex if  for any
for any  .
.
If we consider a bounded sequence  in
in  , we are able to define a function
, we are able to define a function  , called type, such that for each
, called type, such that for each 

The asymptotic center of a bounded sequence with respect to a subset  of
of  is then defined as
is then defined as

If the asymptotic center is taken with respect to  then it is simply denoted by
then it is simply denoted by  .
.
Definition 2.7.
We say that a convexity structure is  -stable if types are
-stable if types are  -convex.
-convex.
In [1] the following definition of compactness for convexity structure was considered.
Definition 2.8.
Given  a convexity structure, we will say that
a convexity structure, we will say that  is compact if any family
is compact if any family  of elements of
of elements of  has nonempty intersection provided
has nonempty intersection provided  for any finite subset
for any finite subset  .
.
In our paper we will rather use the idea of compactness given in [11]. Notice that this second notion of compactness is weaker than the previous one.
Definition 2.9.
Given  a convexity structure, we will say that
a convexity structure, we will say that  is nested compact if any decreasing chain
is nested compact if any decreasing chain  of nonempty bounded elements of
of nonempty bounded elements of  has nonempty intersection.
has nonempty intersection.
A very important property given in [3] about complete uniformly convex metric spaces with monotone modulus of convexity is that decreasing sequences of nonempty bounded closed and convex subsets of these spaces have nonempty intersection. As a consequence, we have that if  stands for the collection of nonempty closed and convex subsets of a complete uniformly convex metric space with monotone modulus of convexity, then
stands for the collection of nonempty closed and convex subsets of a complete uniformly convex metric space with monotone modulus of convexity, then  is a nested compact convexity structure.
is a nested compact convexity structure.
Remark 2.10.
It is not hard to see that the same remains true if the monotone condition on the modulus is replaced by lower semicontinuity from the right.
3. Asymptotic Pointwise Contractions in Uniformly Convex Metric Spaces
In this section we give different results for the above defined mappings in uniformly convex metric spaces. Although, for expository reasons, our results will be usually proved only for uniformly convex metric spaces with a monotone modulus of convexity, they also hold when there is a lower semicontinuous modulus of convexity. Some indications about differences in both cases will be given. We begin with a technical result.
Proposition 3.1.
Let  be a complete uniformly convex metric space with a monotone (or lower semicontinuous from the right) modulus of convexity
be a complete uniformly convex metric space with a monotone (or lower semicontinuous from the right) modulus of convexity  . Consider the family
. Consider the family  of all nonempty closed and convex subsets of
of all nonempty closed and convex subsets of  . Then
. Then  defines a nested compact and
defines a nested compact and  -stable convexity structure on
-stable convexity structure on  .
.
Proof.
It only remains to be proved that  is
is  -stable. Let
-stable. Let  be a bounded sequence in
be a bounded sequence in  and consider the type defined by
and consider the type defined by  . We need to show that
. We need to show that  for any positive
for any positive  . It is immediate to see that
. It is immediate to see that  is closed and nonempty. To see that
is closed and nonempty. To see that  is also convex, consider
is also convex, consider  and
and  to be two different points in
to be two different points in  . There is no restriction if we assume that
. There is no restriction if we assume that  . Let
. Let  be the midpoint of the segment
be the midpoint of the segment  and take
and take  , then, by uniform convexity, we have that
, then, by uniform convexity, we have that

and so,

Hence,  .
.
The following theorems were proved in [1] under the hypothesis of compactness on the convexity structure. We state it, however, under the hypothesis of nested compactness since this is all it is actually required in the proofs given in [1].
Theorem 3.2.
Let  be a bounded metric space. Assume that the convexity structure
be a bounded metric space. Assume that the convexity structure  is nested compact. Let
is nested compact. Let  be a pointwise contraction. Then
be a pointwise contraction. Then  has a unique fixed point
has a unique fixed point  . Moreover the orbit
. Moreover the orbit  converges to
converges to  , for each
, for each  .
.
Theorem 3.3.
Let  be a bounded metric space. Assume that the convexity structure
be a bounded metric space. Assume that the convexity structure  is nested compact. Let
is nested compact. Let  be a strongly asymptotic pointwise contraction. Then
be a strongly asymptotic pointwise contraction. Then  has a unique fixed point
has a unique fixed point  . Moreover the orbit
. Moreover the orbit  converges to
converges to  , for each
, for each  .
.
Now the next corollary follows.
Corollary 3.4.
The above theorems hold for complete bounded uniformly convex metric spaces with either monotone or lower semicontinuous from the right modulus of convexity.
The following lemma is immediate.
Lemma 3.5.
Let  be a metric space and
be a metric space and  a nested compact convexity structure on
a nested compact convexity structure on  which is
which is  -stable. Then for any type
-stable. Then for any type  , there exists
, there exists  such that
such that

As a direct consequence of Proposition 3.1 and the previous lemma we get the following result for asymptotic pointwise contractions. We omit the details of its proof as it follows similar patterns as in [1, Theorem 4.2].
Theorem 3.6.
Let  be a complete uniformly convex metric space with a monotone (or lower semicontinuous from the right) modulus of convexity
be a complete uniformly convex metric space with a monotone (or lower semicontinuous from the right) modulus of convexity  . Suppose
. Suppose  is bounded. Then every
is bounded. Then every  asymptotic pointwise contraction has a unique fixed point
asymptotic pointwise contraction has a unique fixed point  . Moreover, the orbit
. Moreover, the orbit  converges to
converges to  for each
for each  .
.
Next we show some consequences of Proposition 3.1 and Lemma 3.5. The cases for monotone and lower semicontinuous from the right modulus of convexity are shown separately as they require different proofs.
Corollary 3.7.
Let  be a complete uniformly convex metric space with a monotone modulus of convexity and
be a complete uniformly convex metric space with a monotone modulus of convexity and  a bounded sequence in
a bounded sequence in  . Then the set of asymptotic centers of
. Then the set of asymptotic centers of  is a singleton.
is a singleton.
Proof.
Let  and
and  be two different points in
be two different points in  and let
and let  be the midpoint of
be the midpoint of  . Let
. Let  ,
,  and
and  . By the uniform convexity, there exists
. By the uniform convexity, there exists  such that for every
such that for every  ,
,

If we let  go to infinite, we obtain that
go to infinite, we obtain that  which is clearly a contradiction.
which is clearly a contradiction.
Remark 3.8.
This corollary has been first proved in [12, Proposition 3.3] for a certain class of uniformly convex hyperbolic spaces with monotone modulus of convexity.
Now we show the lower semicontinuous case.
Corollary 3.9.
Let  be a complete uniformly convex metric space with a lower semicontinuous from the right modulus of convexity and
be a complete uniformly convex metric space with a lower semicontinuous from the right modulus of convexity and  a bounded sequence in
a bounded sequence in  . Then the set of asymptotic centers of
. Then the set of asymptotic centers of  is a singleton.
is a singleton.
Proof.
Let  and
and  be two different points in
be two different points in  and let
and let  be the midpoint of
be the midpoint of  . Let
. Let  ,
,  and let us fix
and let us fix  . Then
. Then  for each
for each  large enough. By the uniform convexity,
large enough. By the uniform convexity,

for the same  as above and finally
as above and finally

Now it suffices to observe that

for  large enough. Combining it with (3.6) and taking
large enough. Combining it with (3.6) and taking  we obtain
we obtain  as in the former corollary, and thus the contradiction.
as in the former corollary, and thus the contradiction.
Another consequence is Kirk Fixed Point Theorem in uniformly convex metric spaces.
Corollary 3.10.
Let  be a complete uniformly convex geodesic metric space with a monotone (or lower semicontinuous from the right) modulus of convexity. Suppose
be a complete uniformly convex geodesic metric space with a monotone (or lower semicontinuous from the right) modulus of convexity. Suppose  is bounded, then any nonexpansive mapping
is bounded, then any nonexpansive mapping  has a fixed point.
has a fixed point.
Proof.
Consider  and
and  the sequence of its iterates. Let
the sequence of its iterates. Let  be the only asymptotic center of
be the only asymptotic center of  in
in  . Then, by the nonexpansiveness of
. Then, by the nonexpansiveness of  , it follows that
, it follows that  and so,
and so,  .
.
Now we present a counterpart for [1, Theorem 5.1].
Theorem 3.11.
Let  be a complete uniformly convex metric space with a monotone (or lower semicontinuous from the right) modulus of convexity
be a complete uniformly convex metric space with a monotone (or lower semicontinuous from the right) modulus of convexity  . Let
. Let  be a bounded closed convex nonempty subset of
be a bounded closed convex nonempty subset of  . Then any
. Then any  asymptotic pointwise nonexpansive mapping has a fixed point, and the set of fixed points of
asymptotic pointwise nonexpansive mapping has a fixed point, and the set of fixed points of  ,
,  , is closed and convex.
, is closed and convex.
Proof.
Let  and consider
and consider  . From Corollary 3.7, we know that
. From Corollary 3.7, we know that  is a singleton. Let
is a singleton. Let  be the only point in that set, that is,
be the only point in that set, that is,  is such that
is such that  . We want to show that
. We want to show that  is a Cauchy sequence. Suppose this is not the case. Then there exists a separated subsequence
is a Cauchy sequence. Suppose this is not the case. Then there exists a separated subsequence  of
of  , that is, there exists
, that is, there exists  such that
such that  for every
for every  in
in  .
.
Let  be the midpoint of the segment
be the midpoint of the segment  ,
,  and
and  . The uniform convexity of the space, together with its monotone character, implies that for every
. The uniform convexity of the space, together with its monotone character, implies that for every  and
and  in
in 

Notice that, by definition of  ,
,

Then, if we let  go to infinity,
go to infinity,

Since  is pointwise asymptotic nonexpansive, then
is pointwise asymptotic nonexpansive, then

and so  , which is a contradiction since, in virtue of (3.9), this implies that
, which is a contradiction since, in virtue of (3.9), this implies that  converges to
converges to  . Therefore,
. Therefore,  is a Cauchy sequence and its limit, again by (3.9), is
is a Cauchy sequence and its limit, again by (3.9), is  . Then, from the continuity of
. Then, from the continuity of  ,
,  .
.
In consequence,  is nonempty. Now, since
is nonempty. Now, since  is continuous,
is continuous,  is closed. We show next that
is closed. We show next that  is also convex. Let
is also convex. Let  be two different points in
be two different points in  and
and  the midpoint of the segment
the midpoint of the segment  . We need to show that
. We need to show that  . Now, since
. Now, since  is pointwise asymptotic nonexpansive,
is pointwise asymptotic nonexpansive,

and, equally,

Therefore, for  there exists
there exists  such that if
such that if  then
then

but, from the proof of Proposition 2.2 in [3], the diameters of the sets  tend to
tend to  as
as  tends to
tends to  and so
and so  , which proves
, which proves  is a fixed point of
is a fixed point of  .
.
Remark 3.12.
The proof for the lower semicontinuous case follows in a similar way but following the reasoning of Corollary 3.9.
In [1] a demiclosed principle is also given for asymptotic pointwise nonexpansive mappings in CAT(0) spaces. Next we show that an equivalent result is also possible for uniformly convex metric spaces. Following [1] we define

where  is a closed and convex subset of a uniformly convex metric space containing the bounded sequence
is a closed and convex subset of a uniformly convex metric space containing the bounded sequence  . Notice that this definition does not depend on the set
. Notice that this definition does not depend on the set  when the space
when the space  is a complete CAT(0) space. This is due to the fact that the asymptotic center of a bounded sequence of a complete CAT(0) space belongs to the closed convex hull of the sequence, which easily follows from the very well-known fact that the metric projection onto closed convex subsets of a complete CAT(0) space is nonexpansive (see [2] for details). Recall that the existence and uniqueness of such a
is a complete CAT(0) space. This is due to the fact that the asymptotic center of a bounded sequence of a complete CAT(0) space belongs to the closed convex hull of the sequence, which easily follows from the very well-known fact that the metric projection onto closed convex subsets of a complete CAT(0) space is nonexpansive (see [2] for details). Recall that the existence and uniqueness of such a  in a complete uniformly convex metric spaces with monotone modulus of convexity is guaranteed by Corollary 3.7.
in a complete uniformly convex metric spaces with monotone modulus of convexity is guaranteed by Corollary 3.7.
Proposition 3.13.
Let  be a complete uniformly convex metric space with a monotone modulus of convexity
be a complete uniformly convex metric space with a monotone modulus of convexity  . Let
. Let  be a bounded closed convex nonempty subset of
be a bounded closed convex nonempty subset of  . Let
. Let  an asymptotic pointwise nonexpansive mapping. Let
an asymptotic pointwise nonexpansive mapping. Let  be an approximate fixed point sequence, that is,
be an approximate fixed point sequence, that is,  , and such that
, and such that  for a certain
for a certain  . Then
. Then  .
.
Proof.
Since  is an approximate fixed point sequence, then we have that
is an approximate fixed point sequence, then we have that

for any  (see Note Added in Proof at the end of the paper). In consequence, since
(see Note Added in Proof at the end of the paper). In consequence, since  for
for  , (3.9) holds for any
, (3.9) holds for any  .
.
Therefore, particularizing for  , we have that
, we have that  . Now we claim that
. Now we claim that  as
as  . Suppose on the contrary that there exist an
. Suppose on the contrary that there exist an  and a subsequence
and a subsequence  of
of  such that
such that  for every
for every  . Let
. Let  be the midpoint of the geodesic segment
be the midpoint of the geodesic segment  ,
,  and
and  . By uniform convexity, for every
. By uniform convexity, for every  , we have that
, we have that

If we consider the upper limit of the above inequality when  , we get
, we get

If we do the same when  , we finally obtain that
, we finally obtain that  . Therefore
. Therefore  and the existence of fixed point follows the same as in Theorem 3.11.
and the existence of fixed point follows the same as in Theorem 3.11.
Remark 3.14.
The proof for the lower semicontinuous case follows in a similar way but following the reasoning of Corollary 3.9.
4. Fixed Points of Set-Valued Mappings
In this section we present fixed points theorems for set-valued mappings defined on uniformly convex metric spaces. Results stated for uniformly convex metric space with a monotone modulus of convexity also hold if there is a lower semicontinuous from the right modulus of convexity. Proofs of this second case will be omitted as they are based on technical results already proved for both kinds of modulus in Section 3. The Hausdorff metric on the closed and bounded parts of a metric space  is defined as follows. If
is defined as follows. If  and
and  are bounded and closed subsets of a metric space
are bounded and closed subsets of a metric space  , then
, then

where  . Let
. Let  be a subset of a metric space
be a subset of a metric space  . A mapping
. A mapping  with nonempty bounded closed values is nonexpansive if
with nonempty bounded closed values is nonexpansive if

for all  . Our main goal in this section is to study if given
. Our main goal in this section is to study if given  is a bounded uniformly convex metric space with monotone modulus of convexity, then every nonexpansive mapping
is a bounded uniformly convex metric space with monotone modulus of convexity, then every nonexpansive mapping  with nonempty and compact values has a fixed point, that is, a point
with nonempty and compact values has a fixed point, that is, a point  such that
such that  . This problem was first solved in the affirmative by Shimizu and Takahashi in [9] under the assumption that the metric is convex. If we lack this condition the problem is much more complicated and we can offer only partial answers. Our first answer will be achieved after imposing condition (i):
. This problem was first solved in the affirmative by Shimizu and Takahashi in [9] under the assumption that the metric is convex. If we lack this condition the problem is much more complicated and we can offer only partial answers. Our first answer will be achieved after imposing condition (i):
(i)there exists a point  such that for each
such that for each  there is a number
there is a number  such that for all
such that for all  :
:

where  stand for points from geodesic segments
stand for points from geodesic segments  and
and  , respectively, and
, respectively, and  ,
,  .
.
Remark 4.1.
Condition (i) can be seen as a kind of very weak hyperbolicity condition. In fact, it is immediate to see that hyperbolic uniformly convex spaces studied in [3, 10, 12] satisfy condition (i) as well as for any uniformly convex CAT space with
space with  . Notice here that CAT
. Notice here that CAT spaces with
spaces with  are particular examples of hyperbolic uniformly convex spaces.
are particular examples of hyperbolic uniformly convex spaces.
Theorem 4.2.
Let  be a complete uniformly convex metric space with a monotone modulus of convexity. Suppose that
be a complete uniformly convex metric space with a monotone modulus of convexity. Suppose that  is bounded and the condition (i) holds true. Then each nonexpansive set-valued mapping
is bounded and the condition (i) holds true. Then each nonexpansive set-valued mapping  with compact values has a fixed point.
with compact values has a fixed point.
Proof.
Let us fix  satisfying the condition (i). Now, from (i) and the fact that
satisfying the condition (i). Now, from (i) and the fact that  is compact for any
is compact for any  , it follows that set-valued mappings
, it follows that set-valued mappings  ,
,  defined by
defined by

are compact-valued contractions with constants  . Nadler's Fixed Point Theorem for set-valued contractions implies that
. Nadler's Fixed Point Theorem for set-valued contractions implies that  has a fixed point for each
has a fixed point for each  and therefore
and therefore  has an approximate fixed point sequence, that is, a sequence
has an approximate fixed point sequence, that is, a sequence  such that
such that  . According to Corollary 3.7 there is a unique asymptotic center of
. According to Corollary 3.7 there is a unique asymptotic center of  in
in  . Now the rest of the proof follows the same patterns of the standard one for uniformly convex Banach spaces (see [13, Theorem 15.3, page 165]).
. Now the rest of the proof follows the same patterns of the standard one for uniformly convex Banach spaces (see [13, Theorem 15.3, page 165]).
It is wellknown that a CAT(1) space needs not to be uniformly convex if its diameter is not smaller than  . Next we show, however, that the same above idea can be applied to CAT(1) spaces of radius smaller than
. Next we show, however, that the same above idea can be applied to CAT(1) spaces of radius smaller than  . Remember that for
. Remember that for  the number
the number  is defined as
is defined as  and that the radius of a bounded subset
and that the radius of a bounded subset  of
of  is given by
is given by

Theorem 4.3.
Let  and let
and let  be a complete
be a complete  space with
space with  . Then each nonexpansive mapping
. Then each nonexpansive mapping  with compact values has at least one fixed point.
with compact values has at least one fixed point.
Proof.
Take  in such a way that
in such a way that  . As it is shown in [14, Lemma 3], it is enough to take
. As it is shown in [14, Lemma 3], it is enough to take  for
for  to verify condition (i) with
to verify condition (i) with  in
in  . In a similar manner as above we obtain an approximate fixed point sequence
. In a similar manner as above we obtain an approximate fixed point sequence  . On account of
. On account of  and [15, Proposition 4.1] the asymptotic center of each subsequence of
and [15, Proposition 4.1] the asymptotic center of each subsequence of  is unique, and the rest of the proof is not different from the case of uniformly convex Banach spaces.
is unique, and the rest of the proof is not different from the case of uniformly convex Banach spaces.
Next we consider two further conditions to guarantee the existence of fixed points for nonexpansive set-valued mappings with compact values in uniformly convex metric spaces.
-
(ii)
There is a function
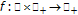 such that
such that 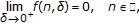 (4.6)
(4.6)
and for all  and
and  ,
,  was chosen in such a way that
was chosen in such a way that  ,
,  and
and  we have
we have

(iii) , where
, where  is, as usual, a monotone modulus of convexity of the space.
is, as usual, a monotone modulus of convexity of the space.
Remark 4.4.
Notice that, roughly speaking, conditions (i) and (ii) give opposite information about the geometry of the space. While condition (i) implies that geodesic emanating from a same point must separate and no matters how fast, condition (ii) imposes a superior bound about how much two geodesics emanating from a same point are allowed to separate. It is easy to see that any geodesic space admitting bifurcating geodesics cannot verify condition (ii). In particular, condition (ii) does not hold in  -trees. It easily follows from the definitions that geodesic spaces with curvature bounded below by a real number
-trees. It easily follows from the definitions that geodesic spaces with curvature bounded below by a real number  (check [16] for a detailed exposition about these spaces) satisfy condition (ii).
(check [16] for a detailed exposition about these spaces) satisfy condition (ii).
Before stating our next result we need to introduce a definition.
Definition 4.5.
A geodesic space  is said to have the geodesic extension property if any geodesic segment in
is said to have the geodesic extension property if any geodesic segment in  is actually contained in a geodesic line, that is, in a geodesic
is actually contained in a geodesic line, that is, in a geodesic  .
.
Theorem 4.6.
Let  be a complete uniformly convex metric space with a monotone modulus of convexity and the geodesic extension property. Moreover, suppose that
be a complete uniformly convex metric space with a monotone modulus of convexity and the geodesic extension property. Moreover, suppose that  satisfies conditions (ii) and (iii) and
satisfies conditions (ii) and (iii) and  is a nonempty bounded closed and convex subset of
is a nonempty bounded closed and convex subset of  . If
. If  is a nonexpansive mappings with compact values then
is a nonexpansive mappings with compact values then  has at least one fixed point.
has at least one fixed point.
Proof.
From the proof of Theorem 4.2, we know that if  then the conclusion follows. So let us suppose that
then the conclusion follows. So let us suppose that

and fix  small enough. Let
small enough. Let  be chosen in such a way that
be chosen in such a way that  and let us denote this distance by
and let us denote this distance by  . Clearly, from the compactness of
. Clearly, from the compactness of  it follows the existence of
it follows the existence of  for which
for which  . Now assume that
. Now assume that  is a midpoint of the metric segment
is a midpoint of the metric segment  . The conditions imposed on
. The conditions imposed on  imply that there is
imply that there is  such that
such that  and
and  .
.
To estimate the distance between  and
and  let us consider the midpoint
let us consider the midpoint  of
of  . Using the uniformly convexity of
. Using the uniformly convexity of  we obtain that
we obtain that

If we denote by  the point of the geodesic ray
the point of the geodesic ray  containing
containing  such that
such that  and
and  , then
, then  and
and

Repeating our reasoning for  ,
,  and
and  , we obtain points
, we obtain points  and
and  satisfying
satisfying

where

If we denote by  the point in
the point in  for which
for which  and
and  , then it is easy to see that
, then it is easy to see that  . Hence
. Hence

The previous procedure gives us induction sequences of points  and numbers
and numbers  such that
such that

and for  fixed, a point
fixed, a point  for which
for which

Next let us fix  and find
and find  such that
such that  . Obviously, according to (ii), one can choose
. Obviously, according to (ii), one can choose  for which
for which

and by (iii) select  such small that
such small that  for all
for all  .
.
Choosing  such that
such that  and repeating our iterative procedure
and repeating our iterative procedure  -times, one may notice that the sequence
-times, one may notice that the sequence  decreases so
decreases so  for each
for each  . Finally we find
. Finally we find  for which, on account of (4.15),
for which, on account of (4.15),

contrary to the boundedness of  . Hence
. Hence  and the result follows.
and the result follows.
From Theorems 3.11 and 4.2 one may get the following generalization of [1, Theorem 5.2]. We omit the proof as it is analog to the one given for CAT(0) spaces in [1]. We first need some notations and definitions.
Let  be a uniformly convex metric space. Consider the mappings
be a uniformly convex metric space. Consider the mappings  and
and  , then
, then  and
and  are said to be commuting mappings if
are said to be commuting mappings if  for all
for all  and for all
and for all  . A point
. A point  is called a center for the mapping
is called a center for the mapping  if for each
if for each  ,
,  . The set
. The set  denotes the set of all centers of the mappings
denotes the set of all centers of the mappings  .
.
Theorem 4.7.
Let  be a bounded and complete uniformly convex space with a monotone modulus of convexity for which condition (i) holds. Suppose that
be a bounded and complete uniformly convex space with a monotone modulus of convexity for which condition (i) holds. Suppose that  is pointwise asymptotically nonexpansive and
is pointwise asymptotically nonexpansive and  a nonexpansive mapping with compact and convex values. If
a nonexpansive mapping with compact and convex values. If  and
and  commute and satisfy the condition
commute and satisfy the condition

then there is  such that
such that  .
.
Remark 4.8.
The same result remains true if the uniformly convex metric space is supposed to have the geodesic extension property, and conditions (ii)-(iii) hold instead of condition (i).
We finish this work with a last remark about a different condition to obtain another version of Theorem 4.6. Let  be a metric space. Then we say that
be a metric space. Then we say that  has the Stečkin property if for
has the Stečkin property if for  and
and  fixed positive numbers there exist
fixed positive numbers there exist  such that if
such that if  satisfy
satisfy  , then
, then

The Stečkin property was introduced in [17] to obtain different results regarding the existence of unique nearest and farthest points to closed subsets of normed linear spaces. This property has been studied by many authors since then being of special relevance in the study of uniformly convex Banach spaces; see for instance [18, 19]. It is known that the Stečkin property does not happen in geodesic spaces with bifurcating geodesics [19, 20] and it has been shown to be related to the property of having curvature bounded below (see [16] for details about spaces with curvature bounded below); see [19, 20]. We next show that this property, in addition to a similar condition to (ii), leads to the existence of fixed points for set-valued nonexpansive mappings. We first introduce condition  :
:
there is a function  such that
such that

and for all  and
and  ,
,  was chosen in such a way that
was chosen in such a way that  ,
,  and
and  we have
we have

Theorem 4.9.
Let  be a complete uniformly convex metric space with a monotone modulus of convexity and the geodesic extension property. Moreover, suppose that
be a complete uniformly convex metric space with a monotone modulus of convexity and the geodesic extension property. Moreover, suppose that  satisfies conditions
satisfies conditions  and the Stečkin property. Let
and the Stečkin property. Let  be a nonempty bounded closed and convex subset of
be a nonempty bounded closed and convex subset of  . If
. If  is a nonexpansive mappings with compact values then
is a nonexpansive mappings with compact values then  has at least one fixed point.
has at least one fixed point.
Proof.
We will omit details for this proof as it follows the same patterns of the proof of Theorem 4.6. We will just point out that the main difference happens when the modulus of convexity is used to estimate  first (see (4.10), and
first (see (4.10), and  later (see (4.15), now we use property S to achieve similar estimations.
later (see (4.15), now we use property S to achieve similar estimations.
Note Added in Proof
To prove (3.16) in Proposition 3.13 we need to ask for something more, in particular, it suffices if we assume that  is uniformly continuous. Under this assumption we can prove by induction that
is uniformly continuous. Under this assumption we can prove by induction that  is an approximate fixed point sequence for each
is an approximate fixed point sequence for each  . Indeed, let
. Indeed, let  ,
,  and choose
and choose  the one given by the uniform continuity of
the one given by the uniform continuity of  . Since
. Since  is an approximate fixed point sequence, there exists
is an approximate fixed point sequence, there exists  such that
such that  for every
for every  . This implies that
. This implies that

for every  . Thus
. Thus  which proves our claim. Suppose now that
which proves our claim. Suppose now that  is an approximate fixed point sequence. We want to see that
is an approximate fixed point sequence. We want to see that  is so too. Given
is so too. Given  we fix
we fix  as in the case
as in the case  . Since
. Since  is an approximate fixed point sequence, there exists
is an approximate fixed point sequence, there exists  such that
such that  for every
for every  . This implies that
. This implies that

for every  . Thus
. Thus  is an approximate fixed point sequence.
is an approximate fixed point sequence.
Now, since

by recalling that  , (3.16) follows.
, (3.16) follows.
References
Hussain N, Khamsi MA: On asymptotic pointwise contractions in Metric spaces. Nonlinear Analysis: Theory, Methods & Applications. In press
Bridson MR, Haefliger A: Metric Spaces of Non-Positive Curvature, Grundlehren der Mathematischen Wissenschaften. Volume 319. Springer, Berlin, Germany; 1999:xxii+643.
Kohlenbach U, Leuştean L: Asymptotically nonexpansive mappings in uniformly convex hyperbolic spaces. to appear in Journal of the European Mathematical Society, http://arxiv.org/abs/0707.1626 to appear in Journal of the European Mathematical Society,
Kirk WA: Some recent results in metric fixed point theory. Journal of Fixed Point Theory and Applications 2007,2(2):195–207. 10.1007/s11784-007-0031-8
Arav M, Castillo Santos FE, Reich S, Zaslavski AJ: A note on asymptotic contractions. Fixed Point Theory and Applications 2007, 2007:-6.
Kirk WA: Fixed points of asymptotic contractions. Journal of Mathematical Analysis and Applications 2003,277(2):645–650. 10.1016/S0022-247X(02)00612-1
Khamsi MA: On asymptotically nonexpansive mappings in hyperconvex metric spaces. Proceedings of the American Mathematical Society 2004,132(2):365–373. 10.1090/S0002-9939-03-07172-7
Kirk WA, Xu H-K: Asymptotic pointwise contractions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4706–4712. 10.1016/j.na.2007.11.023
Shimizu T, Takahashi W: Fixed point theorems in certain convex metric spaces. Mathematica Japonica 1992,37(5):855–859.
Leuştean L: A quadratic rate of asymptotic regularity for CAT(0)-spaces. Journal of Mathematical Analysis and Applications 2007,325(1):386–399. 10.1016/j.jmaa.2006.01.081
Khamsi MA, Kirk WA: An Introduction to Metric Spaces and Fixed Point Theory, Pure and Applied Mathematics. Wiley-Interscience, New York, NY, USA; 2001:x+302.
Leuştean L: Nonexpansive iterations in uniformly convex W -hyperbolic spaces. to appear in Contemporary Mathematics, http://arxiv.org/abs/0810.4117 to appear in Contemporary Mathematics,
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Piątek B: Halpern iteration in spherical spaces. submitted to publication
Espínola R, Fernández-León A:
 -spaces, weak convergence and fixed points Journal of Mathematical Analysis and Applications 2009,353(1):410–427. 10.1016/j.jmaa.2008.12.015
-spaces, weak convergence and fixed points Journal of Mathematical Analysis and Applications 2009,353(1):410–427. 10.1016/j.jmaa.2008.12.015Burago D, Burago Y, Ivanov S: A Course in Metric Geometry, Graduate Studies in Mathematics. Volume 33. American Mathematical Society, Providence, RI, USA; 2001:xiv+415.
Stečkin SB: Approximation properties of sets in normed linear spaces. Revue Roumaine de Mathématiques Pures et Appliquées 1963, 8: 5–18.
de Blasi FS, Myjak J, Papini PL: Porous sets in best approximation theory. Journal of the London Mathematical Society 1991,44(1):135–142. 10.1112/jlms/s2-44.1.135
Kaewcharoen A, Kirk WA: Proximinality in geodesic spaces. Abstract and Applied Analysis 2006, 2006:-10.
Zamfirescu T: On the cut locus in Alexandrov spaces and applications to convex surfaces. Pacific Journal of Mathematics 2004,217(2):375–386. 10.2140/pjm.2004.217.375
Acknowledgments
The two first authors were partially supported by the Ministery of Science and Technology of Spain, Grant BFM 2000-0344-CO2-01 and La Junta de Antalucía Project FQM-127. This work was carried out while the third author was visiting the University of Seville. She acknowledges the kind hospitality of the Departamento de Análisis Matemático. This work is dedicated to W. A. Kirk.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Espínola, R., Fernández-León, A. & Piątek, B. Fixed Points of Single- and Set-Valued Mappings in Uniformly Convex Metric Spaces with No Metric Convexity. Fixed Point Theory Appl 2010, 169837 (2009). https://doi.org/10.1155/2010/169837
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/169837
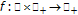 such that
such that 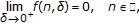
 -spaces, weak convergence and fixed points Journal of Mathematical Analysis and Applications 2009,353(1):410–427. 10.1016/j.jmaa.2008.12.015
-spaces, weak convergence and fixed points Journal of Mathematical Analysis and Applications 2009,353(1):410–427. 10.1016/j.jmaa.2008.12.015