- Research Article
- Open access
- Published:
Existence and Localization Results for 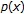 -Laplacian via Topological Methods
-Laplacian via Topological Methods
Fixed Point Theory and Applications volume 2010, Article number: 120646 (2010)
Abstract
We show the existence of a week solution in  to a Dirichlet problem for
to a Dirichlet problem for  in
in  , and its localization. This approach is based on the nonlinear alternative of Leray-Schauder.
, and its localization. This approach is based on the nonlinear alternative of Leray-Schauder.
1. Introduction
In this work, we consider the boundary value problem

where 
 is a nonempty bounded open set with smooth boundary
is a nonempty bounded open set with smooth boundary 
 is the so-called
is the so-called  -Laplacian operator, and (CAR):
-Laplacian operator, and (CAR):  is a Caratheodory function which satisfies the growth condition
is a Caratheodory function which satisfies the growth condition

with  ,
,  for a.e.
for a.e.  , and
, and  ,
,  for a.e.
for a.e.  .
.
We recall in what follows some definitions and basic properties of variable exponent Lebesgue and Sobolev spaces  ,
,  , and
, and  . In that context, we refer to [1, 2] for the fundamental properties of these spaces.
. In that context, we refer to [1, 2] for the fundamental properties of these spaces.
Set

For  let
let  , for a.e.
, for a.e.  .
.
Let us define by  the set of all measurable real functions defined on
the set of all measurable real functions defined on  . For any
. For any  we define the variable exponent Lebesgue space by
we define the variable exponent Lebesgue space by

We define a norm, the so-called Luxemburg norm, on this space by the formula

and  becomes a Banach space.
becomes a Banach space.
The variable exponent Sobolev space  is
is

and we define on this space the norm

for all  The space
The space  is the closure of
is the closure of  in
in  .
.
If  , then the spaces
, then the spaces  ,
,  , and
, and  are separable and reflexive Banach spaces.
are separable and reflexive Banach spaces.
If  and
and  then we have
then we have
(i)
(ii)
(iii)
(iv)
Proposition 1.3 (see [3]).
Assume that  is bounded and smooth. Denote by
is bounded and smooth. Denote by 
(i)Let  . If
. If

then  is compactly imbedded in
is compactly imbedded in 
(ii)(Poincaré inequality, see [1, Theorem  ]). If
]). If  , then there is a constant
, then there is a constant  such that
such that

Consequently,  and
and  are equivalent norms on
are equivalent norms on  . In what follows,
. In what follows,  , with
, with  , will be considered as endowed with the norm
, will be considered as endowed with the norm  .
.
Lemma 1.4.
Assume that  and
and  If
If  , then we have
, then we have

Proof.
By Proposition 1.2( iv), we have

By the mean value theorem, there exists  such that
such that

and we have

Similarly

Remark 1.5.
If  , then
, then

For simplicity of notation, we write

In [4], a topological method, based on the fundamental properties of the Leray-Schauder degree, is used in proving the existence of a week solution in  to the Dirichlet problem (P) that is an adaptation of that used by Dinca et al. for Dirichlet problems with classical
to the Dirichlet problem (P) that is an adaptation of that used by Dinca et al. for Dirichlet problems with classical  -Laplacian [5]. In this work, we use the nonlinear alternative of Leray-Schauder and give the existence of a solution and its localization. This method is used for finding solutions in Hölder spaces, while in [6], solutions are found in Sobolev spaces.
-Laplacian [5]. In this work, we use the nonlinear alternative of Leray-Schauder and give the existence of a solution and its localization. This method is used for finding solutions in Hölder spaces, while in [6], solutions are found in Sobolev spaces.
Let us recall some results borrowed from Dinca [4] about  -Laplacian and Nemytskii operator
-Laplacian and Nemytskii operator  . Firstly, since
. Firstly, since  for all
for all  ,
,  is compactly embedded in
is compactly embedded in  . Denote by
. Denote by  the compact injection of
the compact injection of  in
in  and by
and by 

 ,
,  for all
for all  , its adjoint.
, its adjoint.
Since the Caratheodory function  satisfies (CAR), the Nemytskii operator
satisfies (CAR), the Nemytskii operator  generated by
generated by  ,
,  , is well defined from
, is well defined from  into
into  , continuous, and bounded ([3, Proposition
, continuous, and bounded ([3, Proposition  ]). In order to prove that problem (P) has a weak solution in
]). In order to prove that problem (P) has a weak solution in  it is sufficient to prove that the equation
it is sufficient to prove that the equation

has a solution in  .
.
Indeed, if  satisfies (1.16) then, for all
satisfies (1.16) then, for all  , one has
, one has

which rewrites as

and tells us that  is a weak solution in
is a weak solution in  to problem (P)
to problem (P)
Since  is a homeomorphism of
is a homeomorphism of  onto
onto  (1.16) may be equivalently written as
(1.16) may be equivalently written as

Thus, proving that problem (P) has a weak solution in  reduces to proving that the compact operator
reduces to proving that the compact operator

has a fixed point.
Theorem 1.6 (Alternative of Leray-Schauder, [7]).
Let  denote the closed ball in a Banach space
denote the closed ball in a Banach space  and let
and let  be a compact operator. Then either
be a compact operator. Then either
(i)the equation  has a solution in
has a solution in  for
for  or
or
(ii)there exists an element  with
with  satisfying
satisfying  for some
for some 
2. Main Results
In this work, we present new existence and localization results for  -solutions to problem (P), under (CAR) condition on
-solutions to problem (P), under (CAR) condition on  Our approach is based on regularity results for the solutions of Dirichlet problems and again on the nonlinear alternative of Leray-Schauder.
Our approach is based on regularity results for the solutions of Dirichlet problems and again on the nonlinear alternative of Leray-Schauder.
We start with an existence and localization principle for problem (P).
Theorem 2.1.
Assume that there is a constant  independent of
independent of  , with
, with  for any solution
for any solution  to
to


and for each  . Then the Dirichlet problem (P) has at least one solution
. Then the Dirichlet problem (P) has at least one solution  with
with 
Proof.
By [3, Theorem  ],
],  is a homeomorphism of
is a homeomorphism of  onto
onto  We will apply Theorem 2.1 to
We will apply Theorem 2.1 to  and to operator
and to operator 

where  is given by
is given by  . Notice that, according to a well-known regularity result [4], the operator
. Notice that, according to a well-known regularity result [4], the operator  from
from  to
to  is well defined, continuous, and order preserving. Consequently,
is well defined, continuous, and order preserving. Consequently,  is a compact operator. On the other hand, it is clear that the fixed points of
is a compact operator. On the other hand, it is clear that the fixed points of  are the solutions of problem (P). Now the conclusion follows from Theorem 1.6 since condition (ii) is excluded by hypothesis.
are the solutions of problem (P). Now the conclusion follows from Theorem 1.6 since condition (ii) is excluded by hypothesis.
Theorem 2.2 immediately yields the following existence and localization result.
Theorem 2.2.
Let  , be a smooth bounded domain and let
, be a smooth bounded domain and let  be such that
be such that  for all
for all  . Assume that
. Assume that  is a Caratheodory function which satisfies the growth condition (CAR)
is a Caratheodory function which satisfies the growth condition (CAR)
Suppose, in addition, that

where  is the constant appearing in condition (CAR). Let
is the constant appearing in condition (CAR). Let  be a constant such that
be a constant such that

Then the Dirichlet problem (P) has at least a solution in  with
with 
Proof.
Let  be a solution of problem (
be a solution of problem ( ) with
) with  , corresponding to some
, corresponding to some  . Then by Propositions 1.2, 1.3, and Lemma 1.4, we obtain
. Then by Propositions 1.2, 1.3, and Lemma 1.4, we obtain

Therefore, we have

Substituting  in the above inequality, we obtain
in the above inequality, we obtain

which, taking into account (2.3) and  gives
gives

a contradiction. Theorem 2.1 applies.
References
Fan X, Zhao D: On the spaces
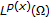 and
and  Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617
Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617Kováčik O, Rákosník J: On spaces
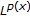 and
and  Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.
Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.Fan X-L, Zhang Q-H: Existence of solutions for
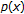 -Laplacian Dirichlet problem Nonlinear Analysis: Theory, Methods & Applications 2003,52(8):1843–1852. 10.1016/S0362-546X(02)00150-5
-Laplacian Dirichlet problem Nonlinear Analysis: Theory, Methods & Applications 2003,52(8):1843–1852. 10.1016/S0362-546X(02)00150-5Dinca G: A fixed point method for the
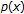 -Laplacian Comptes Rendus Mathématique 2009,347(13–14):757–762. 10.1016/j.crma.2009.04.022
-Laplacian Comptes Rendus Mathématique 2009,347(13–14):757–762. 10.1016/j.crma.2009.04.022Dinca G, Jebelean P, Mawhin J: Variational and topological methods for Dirichlet problems with -Laplacian. Portugaliae Mathematica 2001,58(3):339–378.
O'Regan D, Precup R: Theorems of Leray-Schauder Type and Applications, Series in Mathematical Analysis and Applications. Volume 3. Gordon and Breach, Amsterdam, The Netherlands; 2001:x+206.
Dugundji J, Granas A: Fixed Point Theory. I, Monografie Matematyczne. Volume 61. PWN-Polish Scientific, Warsaw, Poland; 1982:209.
Acknowledgment
The authors would like to thank the referees for their valuable and useful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cekic, B., Mashiyev, R. Existence and Localization Results for 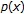 -Laplacian via Topological Methods.
Fixed Point Theory Appl 2010, 120646 (2010). https://doi.org/10.1155/2010/120646
-Laplacian via Topological Methods.
Fixed Point Theory Appl 2010, 120646 (2010). https://doi.org/10.1155/2010/120646
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/120646
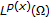 and
and  Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617
Journal of Mathematical Analysis and Applications 2001,263(2):424–446. 10.1006/jmaa.2000.7617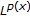 and
and  Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.
Czechoslovak Mathematical Journal 1991,41(116)(4):592–618.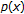 -Laplacian Dirichlet problem Nonlinear Analysis: Theory, Methods & Applications 2003,52(8):1843–1852. 10.1016/S0362-546X(02)00150-5
-Laplacian Dirichlet problem Nonlinear Analysis: Theory, Methods & Applications 2003,52(8):1843–1852. 10.1016/S0362-546X(02)00150-5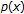 -Laplacian Comptes Rendus Mathématique 2009,347(13–14):757–762. 10.1016/j.crma.2009.04.022
-Laplacian Comptes Rendus Mathématique 2009,347(13–14):757–762. 10.1016/j.crma.2009.04.022