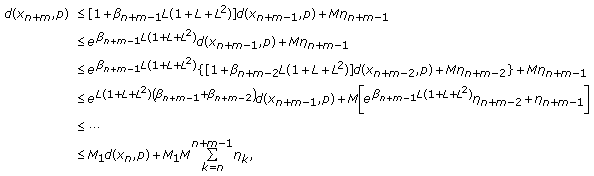- Research Article
- Open access
- Published:
Convergence Theorems of Three-Step Iterative Scheme for a Finite Family of Uniformly Quasi-Lipschitzian Mappings in Convex Metric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 891965 (2009)
Abstract
We consider a new Noor-type iterative procedure with errors for approximating the common fixed point of a finite family of uniformly quasi-Lipschitzian mappings in convex metric spaces. Under appropriate conditions, some convergence theorems are proved for such iterative sequences involving a finite family of uniformly quasi-Lipschitzian mappings. The results presented in this paper extend, improve and unify some main results in previous work.
1. Introduction and Preliminaries
Takahashi [1] introduced a notion of convex metric spaces and studied the fixed point theory for nonexpansive mappings in such setting. For the convex metric spaces, Kirk [2] and Goebel and Kirk [3] used the term "hyperbolic type space" when they studied the iteration processes for nonexpansive mappings in the abstract framework. For the Banach space, Petryshyn and Williamson [4] proved a sufficient and necessary condition for Picard iterative sequences and Mann iterative sequence to converge to fixed points for quasi-nonexpansive mappings. In 1997, Ghosh and Debnath [5] extended the results of [4] and gave the sufficient and necessary condition for Ishikawa iterative sequence to converge to fixed points for quasi-nonexpansive mappings. Liu [6–8] proved some sufficient and necessary conditions for Ishikawa iterative sequence and Ishikawa iterative sequence with errors to converge to fixed point for asymptotically quasi-nonexpansive mappings in Banach space and uniform convex Banach space. Tian [9] gave some sufficient and necessary conditions for an Ishikawa iteration sequence for an asymptotically quasi-nonexpansive mapping to converge to a fixed point in convex metric spaces. Very recently, Wang and Liu [10] gave some iteration sequence with errors to approximate a fixed point of two uniformly quasi-Lipschitzian mappings in convex metric spaces. The purpose of this paper is to give some sufficient and necessary conditions for a new Noor-type iterative sequence with errors to approximate a common fixed point for a finite family of uniformly quasi-Lipschitzian mappings in convex metric spaces. The results presented in this paper generalize, improve, and unify some main results of [1–14].
First of all, let us list some definitions and notations.
Let  be a given self mapping of a nonempty convex subset
be a given self mapping of a nonempty convex subset  of an arbitrary real normed space.The sequence
of an arbitrary real normed space.The sequence  defined by
defined by

is called the Noor iterative procedure with errors [11], where  and
and  are appropriate sequences in [
are appropriate sequences in [ ] with
] with  and
and  ,
, , and
, and  are bounded sequences in
are bounded sequences in  . If
. If  then (1.1) reduces to the Ishikawa iterative procedure with errors [15] defined as follows:
then (1.1) reduces to the Ishikawa iterative procedure with errors [15] defined as follows:

If  then (1.2) reduces to the following Mann type iterative procedure with errors [15]:
then (1.2) reduces to the following Mann type iterative procedure with errors [15]:

Let  be a metric space. A mapping
be a metric space. A mapping  is said to be asymptotically nonexpansive, if there exists a sequence
is said to be asymptotically nonexpansive, if there exists a sequence  [1,
[1, ]
] , such that
, such that

Let  be the set of fixed points of
be the set of fixed points of  in
in  and
and  , a mapping
, a mapping  is said to be asymptotically quasi-nonexpansive, if there exists
is said to be asymptotically quasi-nonexpansive, if there exists  with
with  such that
such that

Moreover,  is said to be uniformly quasi-Lipschitzian, if there exists
is said to be uniformly quasi-Lipschitzian, if there exists  such that
such that

Remark 1.1.
If  is nonempty, then it follows from the above definitions that an asymptotically nonexpansive mapping must be asymptotically quasi-nonexpansive, and an asymptotically quasi-nonexpansive mapping must be a uniformly quasi-Lipschitzian with
is nonempty, then it follows from the above definitions that an asymptotically nonexpansive mapping must be asymptotically quasi-nonexpansive, and an asymptotically quasi-nonexpansive mapping must be a uniformly quasi-Lipschitzian with  . However, the inverse is not true in general.
. However, the inverse is not true in general.
Definition 1.2 (see [ 9]).
Let  be a metric space, and let
be a metric space, and let  [0,1],
[0,1], ,
, ,
, be real sequences in [
be real sequences in [ ] with
] with  . A mapping
. A mapping  is said to be a convex structure on
is said to be a convex structure on  if, for any
if, for any  and
and  ,
,

If  is a metric space with a convex structure
is a metric space with a convex structure  , then
, then  is called a convex metric space. Let
is called a convex metric space. Let  be a convex metric space, a nonempty subset
be a convex metric space, a nonempty subset  of
of  is said to be convex if
is said to be convex if

Definition 1.3.
Let  be a convex metric space with a convex structure
be a convex metric space with a convex structure  and
and  be a finite family of uniformly quasi-Lipschitzian mappings with
be a finite family of uniformly quasi-Lipschitzian mappings with  . Let
. Let  ,
, ,
, , and
, and  be nine sequences in [
be nine sequences in [ with
with

For a given  define a sequence
define a sequence  as follows:
as follows:

where  ,
, is a Lipschitz continuous mapping with a Lipschitz constant
is a Lipschitz continuous mapping with a Lipschitz constant  and
and  ,
, are any given three sequences in
are any given three sequences in  Then
Then  is called the Noor-type iterative sequence with errors for a finite family of uniformly quasi-Lipschitzian mappings
is called the Noor-type iterative sequence with errors for a finite family of uniformly quasi-Lipschitzian mappings  . If
. If 
 in (1.10), then the sequence
in (1.10), then the sequence  defined by (1.10) can be written as follows:
defined by (1.10) can be written as follows:

If  for all
for all  in (1.10), then
in (1.10), then  for all
for all  and the sequence
and the sequence  defined by (1.10) can be written as follows:
defined by (1.10) can be written as follows:

If  and
and  for all
for all  , then the sequence
, then the sequence  defined by (1.10) can be written as follows:
defined by (1.10) can be written as follows:

which is the Ishikawa type iterative sequence with errors considered in [9]. Further, if  and
and  for all
for all  , then
, then  for all
for all  and (1.10) reduces to the following Mann type iterative sequence with errors [9]:
and (1.10) reduces to the following Mann type iterative sequence with errors [9]:

In order to prove our main results, the following lemmas will be needed.
Lemma 1.4.
Let  be a convex metric space,
be a convex metric space,  be a uniformly quasi-Lipschitzian mapping for
be a uniformly quasi-Lipschitzian mapping for  such that
such that  . Then there exists a constant
. Then there exists a constant  such that, for all
such that, for all 

Proof.
In fact, for each  , since
, since  is a uniformly quasi-Lipschitzian mapping, we have
is a uniformly quasi-Lipschitzian mapping, we have

where

This completes the Proof.
Lemma 1.5 (see [7]).
Let  be three nonexpansive squences satisfying the following conditions:
be three nonexpansive squences satisfying the following conditions:

Then
(1) exists;
exists;
(2)In addition, if  , then
, then  .
.
Lemma 1.6.
Let  be a complete convex metric space and
be a complete convex metric space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a finite family of uniformly quasi-Lipschitzian mapping for
be a finite family of uniformly quasi-Lipschitzian mapping for  such that
such that  and
and  be a contractive mapping with a contractive constant
be a contractive mapping with a contractive constant  Let
Let  be the iterative sequence with errors defined by (1.10) and
be the iterative sequence with errors defined by (1.10) and  ,
,  be three bounded sequences in
be three bounded sequences in  . Let
. Let  ,
, ,
, ,
,  be sequences in [0,1] satisfying the following conditions:
be sequences in [0,1] satisfying the following conditions:
(i) ;
;
(ii) ;
;
(iii)
Then the following conclusions hold:
(1)for all and
and  ,
,

where ,
,  for all
for all and
and

(2)there exists a constant such that
such that

for all .
.
Proof.
-
(1)
It follows from (1.7),(1.10), and Lemma 1.4 that
 (1.22)
(1.22)


Substituting (1.23) into (1.22) and simplifying it, we have

Substituting (1.24) into (1.25) and simplifying it, we get

where

-
(2)
Since
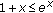 for all
for all  , it follows from (1.26) that, for
, it follows from (1.26) that, for 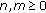 and
and  ,
, 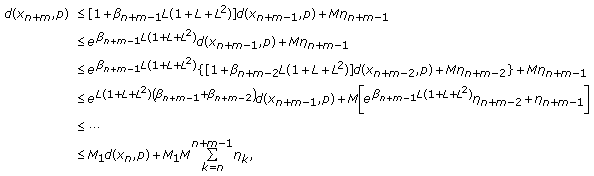 (1.28)
(1.28)
where

This completes the proof.
2. Main Results
Theorem 2.1.
Let  be a complete convex metric space and
be a complete convex metric space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be a finite family of uniformly quasi-Lipschitzian mapping for
be a finite family of uniformly quasi-Lipschitzian mapping for  such that
such that  and
and  be a contractive mapping with a contractive constant
be a contractive mapping with a contractive constant  . Let
. Let  be the iterative sequence with errors defined by (1.10) and
be the iterative sequence with errors defined by (1.10) and  ,
, ,
, be three bounded sequence in
be three bounded sequence in  and
and  ,
, ,
, ,
, ,
, ,
, ,
, ,
, and
and  be nine sequences in [ 0,1] satisfying the following conditions:
be nine sequences in [ 0,1] satisfying the following conditions:
(i) ,
, ,
,
(ii) ,
,
(iii) .
.
Then the sequence  converges to a common fixed point
converges to a common fixed point  if and only if
if and only if  , where
, where 
Proof.
The necessity is obvious. Now prove the sufficiency. In fact, from Lemma 1.6, we have

where  . By conditions (i) and (ii), we know that
. By conditions (i) and (ii), we know that

It follows from Lemma 1.5 that  exists. Since
exists. Since  , we have
, we have

Next prove that  is a Cauchy sequence in
is a Cauchy sequence in  . In fact, for any given
. In fact, for any given  , there exists a positive integer
, there exists a positive integer  such that
such that

From (2.4), there exist  and positive integer
and positive integer  such that
such that

Thus Lemma 1.6 implies that, for any positive integers  with
with  ,
,

This shows that  is a Cauchy sequence in a nonempty closed convex subset
is a Cauchy sequence in a nonempty closed convex subset  of a complete convex metric space
of a complete convex metric space  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  Next prove that
Next prove that  . In fact, for any given
. In fact, for any given  , there exists a positive integer
, there exists a positive integer  such that for all
such that for all  ,
,

Again from (2.7), there exist  and positive integer
and positive integer  such that
such that

Thus, for any  , from (2.7) and (2.8), we have
, from (2.7) and (2.8), we have

By the arbitrariness of  , we know that
, we know that  for all
for all  , that is,
, that is,  . This completes the Proof of Theorem 2.1.
. This completes the Proof of Theorem 2.1.
Taking  in Theorem 2.1, then we have the following theorem.
in Theorem 2.1, then we have the following theorem.
Theorem 2.2.
Let  be a complete convex metric space and
be a complete convex metric space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be a finite family of uniformly quasi-Lipschitzian mapping for
be a finite family of uniformly quasi-Lipschitzian mapping for  such that
such that  . Let
. Let  be the iterative sequence with errors defined by (1.11) and
be the iterative sequence with errors defined by (1.11) and  ,
, ,
, be three bounded sequence in
be three bounded sequence in  , and
, and  ,
, ,
, ,
, ,
, ,
, ,
, ,
, and
and  be nine sequence in [ 0,1] satisfying the conditions (i)–(iii) of Theorem 2.1. Then the sequence
be nine sequence in [ 0,1] satisfying the conditions (i)–(iii) of Theorem 2.1. Then the sequence  converges to a common fixed point
converges to a common fixed point  if and only if
if and only if

where 
Taking  in Theorem 2.1, then we have the following theorem.
in Theorem 2.1, then we have the following theorem.
Theorem 2.3.
Let  be a complete convex metric space and
be a complete convex metric space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a finite family of uniformly quasi-Lipschitzian mapping for
be a finite family of uniformly quasi-Lipschitzian mapping for  such that
such that  and
and  be a contractive mapping with a contractive constant
be a contractive mapping with a contractive constant  .
.  Let
Let  be the iterative sequence with errors defined by (1.12) and
be the iterative sequence with errors defined by (1.12) and  ,
, be two bounded sequences in
be two bounded sequences in  and
and  ,
, ,
, ,
, ,
, ,
, be nine sequences in [
be nine sequences in [  ] satisfying the conditions (ii) and (iii) of Theorem 2.1 and
] satisfying the conditions (ii) and (iii) of Theorem 2.1 and  for all
for all  . Then the sequence
. Then the sequence  converges to a common fixed point
converges to a common fixed point  if and only if
if and only if

where 
Remark 2.4.
Theorems 2.1–2.3 generalize, improve, and unify some corresponding results in [1–14].
Similarly, we can obtain the following results.
Theorem 2.5.
Let  be a complete convex metric space and
be a complete convex metric space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a finite family of asymptotically quasi-nonexpansive mapping for
be a finite family of asymptotically quasi-nonexpansive mapping for  such that
such that  and
and  be a contractive mapping with a contractive constant
be a contractive mapping with a contractive constant  . Let
. Let  be the iterative sequence with errors defined by (1.10) and
be the iterative sequence with errors defined by (1.10) and  ,
, ,
, be three bounded sequences in
be three bounded sequences in  and
and  ,
, ,
, ,
, ,
, ,
, , and
, and  be nine sequences in [
be nine sequences in [ ] satisfying the conditions (i)–(iii) of Theorem 2.1. Then the sequence
] satisfying the conditions (i)–(iii) of Theorem 2.1. Then the sequence  converges to a common fixed point
converges to a common fixed point  if and only if
if and only if

where 
Proof.
From Remark 1.1, we know that each asymptotically quasi-nonexpansive mapping  must be a uniformly quasi-Lipschitzian with
must be a uniformly quasi-Lipschitzian with

where  is the sequence appeared in (1.5). Hence the conclusion of Theorem 2.5 can be obtained from Theorem 2.1 immediately. This completes the Proof.
is the sequence appeared in (1.5). Hence the conclusion of Theorem 2.5 can be obtained from Theorem 2.1 immediately. This completes the Proof.
Theorem 2.6.
Let  be a complete convex metric space and
be a complete convex metric space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a finite family of asymptotically quasi-nonexpansive mapping for,
be a finite family of asymptotically quasi-nonexpansive mapping for,  such that
such that  . Let
. Let  be the iterative sequence with errors defined by (1.11) and
be the iterative sequence with errors defined by (1.11) and  ,
, ,
, be three bounded sequence in
be three bounded sequence in  and
and  ,
, ,
, ,
, ,
, ,
, ,
, , and
, and  be nine sequence in [
be nine sequence in [ ] satisfying the conditions (i)–(iii) of Theorem 2.1. Then the sequence
] satisfying the conditions (i)–(iii) of Theorem 2.1. Then the sequence  converges to a common fixed point
converges to a common fixed point  if and only if
if and only if

where 
References
Takahashi W: A convexity in metric space and nonexpansive mappings. I. Kōdai Mathematical Seminar Reports 1970, 22: 142–149. 10.2996/kmj/1138846111
Kirk WA: Krasnoselskii's iteration process in hyperbolic space. Numerical Functional Analysis and Optimization 1982,4(4):371–381. 10.1080/01630568208816123
Goebel K, Kirk WA: Iteration processes for nonexpansive mappings. In Topological Methods in Nonlinear Functional Analysis (Toronto, Canada, 1982), Contemporary Mathematics. Volume 21. American Mathematical Society, Providence, RI, USA; 1983:115–123.
Petryshyn WV, Williamson, TE Jr.: Strong and weak convergence of the sequence of successive approximations for quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 1973, 43: 459–497. 10.1016/0022-247X(73)90087-5
Ghosh MK, Debnath L: Convergence of Ishikawa iterates of quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 1997,207(1):96–103. 10.1006/jmaa.1997.5268
Liu Q: Iterative sequences for asymptotically quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 2001,259(1):1–7. 10.1006/jmaa.2000.6980
Liu Q: Iterative sequences for asymptotically quasi-nonexpansive mappings with error member. Journal of Mathematical Analysis and Applications 2001,259(1):18–24. 10.1006/jmaa.2000.7353
Liu Q: Iteration sequences for asymptotically quasi-nonexpansive mapping with an error member of uniform convex Banach space. Journal of Mathematical Analysis and Applications 2002,266(2):468–471. 10.1006/jmaa.2001.7629
Tian Y-X: Convergence of an Ishikawa type iterative scheme for asymptotically quasi-nonexpansive mappings. Computers & Mathematics with Applications 2005,49(11–12):1905–1912. 10.1016/j.camwa.2004.05.017
Wang C, Liu LW: Convergence theorems for fixed points of uniformly quasi-Lipschitzian mappings in convex metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):2067–2071. 10.1016/j.na.2008.02.106
Cho YJ, Zhou H, Guo G: Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings. Computers & Mathematics with Applications 2004,47(4–5):707–717. 10.1016/S0898-1221(04)90058-2
Fukhar-ud-din H, Khan SH: Convergence of iterates with errors of asymptotically quasi-nonexpansive mappings and applications. Journal of Mathematical Analysis and Applications 2007,328(2):821–829. 10.1016/j.jmaa.2006.05.068
Jeong JU, Kim SH: Weak and strong convergence of the Ishikawa iteration process with errors for two asymptotically nonexpansive mappings. Applied Mathematics and Computation 2006,181(2):1394–1401. 10.1016/j.amc.2006.03.008
Zhou H, Kang JI, Kang SM, Cho YJ: Convergence theorems for uniformly quasi-Lipschitzian mappings. International Journal of Mathematics and Mathematical Science 2004,2004(15):763–775. 10.1155/S0161171204309269
Xu Y: Ishikawa and Mann iterative processes with errors for nonlinear strongly accretive operator equations. Journal of Mathematical Analysis and Applications 1998,224(1):91–101. 10.1006/jmaa.1998.5987
Acknowledgment
The authors would like to express their thanks to the referees for their helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
You-xian, T., Chun-de, Y. Convergence Theorems of Three-Step Iterative Scheme for a Finite Family of Uniformly Quasi-Lipschitzian Mappings in Convex Metric Spaces. Fixed Point Theory Appl 2009, 891965 (2009). https://doi.org/10.1155/2009/891965
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/891965

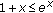 for all
for all  , it follows from (1.26) that, for
, it follows from (1.26) that, for 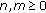 and
and  ,
,